利用GPS、InSAR等大地测量观测资料确定断层的滑移分布是研究地震震间、同震和震后物理过程的基础。断层滑移分布反演问题可描述为:
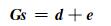
|
(1) |
式中,G为格林函数,其意义为断层上单位滑移分量引起的变形; s为滑移矢量; d为观测的地表位移; e为模型空间(等式左边)和数据空间之间的距离。格林函数与地球模型有关,可以由均匀半无限空间[1-2]、分层半无限空间[3]以及球体分层地球[4-5]等解析或半解析方法得到。
由大地测量观测数据d确定滑移分布s是一个典型的地球物理反演问题。理论上,该问题可以用最小二乘方法得到,但实际反演时最小二乘过拟合的特点会使得反演的断层滑移分布出现不合理的反向滑动。为此,对断层面施加平滑约束:
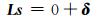
|
(2) |
式中,L为平滑约束算子(正则化矩阵),可以是单位矩阵I、梯度算子∇或Laplace算子∇2,可以分别通过计算向前和中心差分得到[6-7]; δ为滑移模型的粗糙度。其中,梯度算子和Laplace算子都能够约束断层面相邻子断层之间的光滑性,且反演效果无太大差异[8]。在实际反演中,Laplace算子具有具体的物理意义,式(2)即为地震事件的应力降最小,故使用较为广泛[9]。
反演实际地震断层滑移时,由于滑移分布形状并不规则,往往选取较大的断层面。施加平滑约束式(2)后,有时仍然无法避免靠近断层边缘处的反向滑移,也无法得到集中的滑移分布形状。为了解决上述问题,需要再施加非负约束:

|
(3) |
综合式(1)~(3),利用大地测量数据反演断层滑移模型的目标函数可以写为:
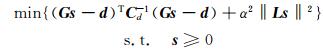
|
(4) |
式中,Cd为观测数据的协方差矩阵; α为平滑因子,可以由多个手段估计得到,例如,根据L-曲线的拐角点[10]、广义交叉验证[11]以及赤池-贝叶斯信息准则(ABIC) [6, 12]。ABIC方法是从统计学角度,以Bayes估计为基础,通过在一维空间搜索ABIC的最小值来确定平滑因子。该方法除了一维空间搜索之外均为解析式,计算速度很快。但在非负约束条件下,ABIC过程中的模型空间积分不再能够解析得到,故该方法不再严格成立。针对该问题,Fukuda等[13]提出一个完全Bayes反演方法,其采用更加合理的MCMC(Markov chain Monte Carlo)采样,被用于解决一些非负约束问题[8, 14-15]。
1 断层滑移分布反演的MCMC方法 1.1 Bayes估计假设式(1)中的e满足e ~N(0, σ2Cd), 式(2)中的δ满足δ ~N(0, ρ2I),其中σ2和ρ2是未知尺度因子,α2=σ2/ρ2。因此,滑移分布的粗糙度由ρ2控制,ρ2越小,对应的滑移分布越平滑,反之亦然。
给定未知滑移向量s和尺度因子σ2,数据向量d的概率密度函数可以用高斯分布表示[6]:
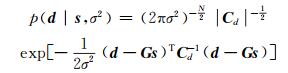
|
(5) |
类似地,也可以写出式(2)的概率密度函数。给定ρ2,滑移分布s的概率密度函数用高斯分布表示为[6, 13]:
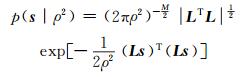
|
(6) |
式中,|·|表示矩阵的行列式。
给定数据向量d,模型s后验概率密度函数可以通过贝叶斯定理用先验概率密度表达:
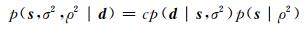
|
(7) |
式中,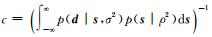

|
(8) |
式中, f(s)是目标函数:
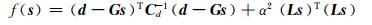
|
(9) |
ABIC的定义为[16]:
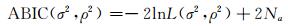
|
(10) |
式中,Na是常数,可以忽略。L(σ2, ρ2)是边缘似然函数:
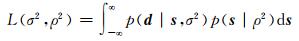
|
(11) |
对于无非负约束的问题,式(11)右端的积分可以有解析表达式[6]:
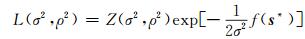
|
(12) |
式中,
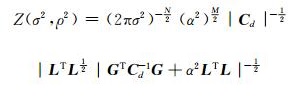
|
(13) |
可以证明,后验概率密度函数是一个均值为最优解s*、协方差阵为σ2(GTCd-1G +α2LTL)-1的M维高斯分布。通过求边缘似然函数L(σ2, ρ2)的最大可以得ABIC的最小。一旦由最小化ABIC得到最优的平滑因子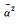
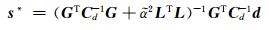
|
(14) |
ABIC方法可以给出最优的平滑因子,但如果考虑非负约束条件,式(11)右端的积分在[0, ∞]不再能解析得到[13]。引入一个基于MCMC采样的贝叶斯反演方法来得到后验概率密度收敛的平均滑移分布,非负约束下的断层滑移后验概率密度函数为:
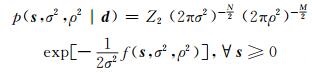
|
(15) |
式中,Z2是与s、σ2、ρ2无关的正规化常数。后验概率密度分布可用MCMC采样方法得到。不同于ABIC方法,完全的贝叶斯反演需要对滑移量s和超参数σ2、ρ2一起置于状态空间采样。
令xt=(s, σ2, ρ2)是t时刻的随机变量,如果下一时刻状态之间的转换概率只依赖当前时刻,那么这个随机变化被称为一个Markov过程:
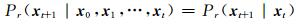
|
(16) |
一个Markov随机过程{ x0, x1, …, xt}是一条Markov链。在一种随机游走的MCMC算法中,当前状态x i只通过转换概率依赖于前一状态。当一条Markov链转化概率满足一定的条件时,该链可以收敛到概率密度。本文采用一种常用的Metropolis-Hastings采样算法来生成Markov链[13]:
1) 令x =(s, σ2, ρ2)为系统状态,初始化t=0,并给定初始状态x(0)。
2) 在区间[x(t)-Δx, x(t)+Δx]根据推荐密度q(x′ | x(t))选出候选状态x′,推荐密度按照均匀随机分布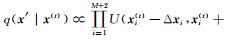

3) 如果σ′2≤0或α′2≤0或s′i≤0,则拒绝候选状态x′,x(t+1)= x(t),t=t+1,返回第2)步。
4) 计算可接受概率
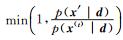
5) 生成[0, 1]上的随机数λ,使得λ~N(0, 1)。
6) 如果λ≤Paccept,则接受候选状态x(t+1)= x′; 否则拒之,x(t+1)= x(t); t=t+1,返回第2)步。
需要指出的是,在步骤4)中,候选状态的接受概率一般表达为Paccept=min(1, 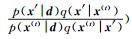
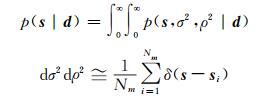
|
(17) |
根据期望和方差的定义可得:
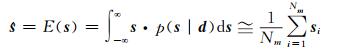
|
(18) |
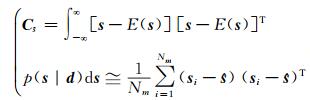
|
(19) |
由于p(s | d)不再是高斯概率密度函数,协方差矩阵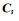
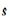
该算法的收敛跟初始状态和状态间隔有关。计算时,可先任意给定平滑因子,然后用非负最小二乘解作为初始状态,采样间隔则与状态空间尺度有关,需人为设定。为了让可接受的解都为合理解,根据Fukuda等[13]的建议,在计算时先燃烧掉一段Markov链,取之后的链作为采样点并重采样,最终求得采样的可接受模型的平均。
利用上述MCMC方法解决反演问题时,若先验约束太强且与观测数据冲突,会引起多峰的后验分布,即解的不唯一性。一旦目标分布是多峰的,选取的模型初值靠近其中的一个解,Markov链将长时间滞留在参数空间的局部区域,陷入局部最小。本文采取模拟退火方法来改进上述MCMC法。
1.4 改进的MCMC方法模拟退火法可以用于寻找具有多峰的复杂函数的最大值。与MCMC方法类似,模拟退火法同样是利用Markov链的特性接受合理的概率探索整个模型空间。与Metropolis-Hastings采样方法不同的是对接受概率进行温度冷却,使其收敛更快。接受概率可以写为:
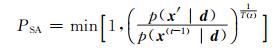
|
(20) |
式中,T(t)为冷却进度,如果T(t)=1,则退化为Metropolis采样。假设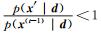
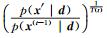
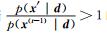
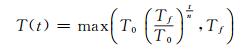
|
(21) |
式(21)意味着从起始温度T0经过n步冷却到最终温度Tf,且剩下的所有采样均保持Tf温度。故模拟退火算法只需要修改Metropolis-Hastings方法中的接受概率计算即可。改进的MCMC算法如下:
1) 令x =(s, σ2, ρ2)为系统状态,初始化t=0,给定初始状态x(0),设置初始温度T0。
2) 在区间[x(t)-Δx, x(t)+Δx]上根据推荐密度q(x′ | x(t))选出候选状态x′,推荐密度按照均匀随机分布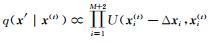
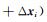
3) 如果σ′2≤0或α′2≤0或s′i≤0,则拒绝候选状态x′,x(t+1)= x(t),t=t+1,返回第2)步。
4) 计算候选状态该点的温度T(t)= 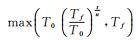
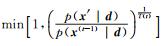
5) 生成[0, 1]上的随机数λ,使得λ~N(0, 1)。
6) 如果λ≤PSA,则接受候选状态x(t+1)= x′; 否则拒之,x(t+1)= x(t); t=t+1,返回第2)步。
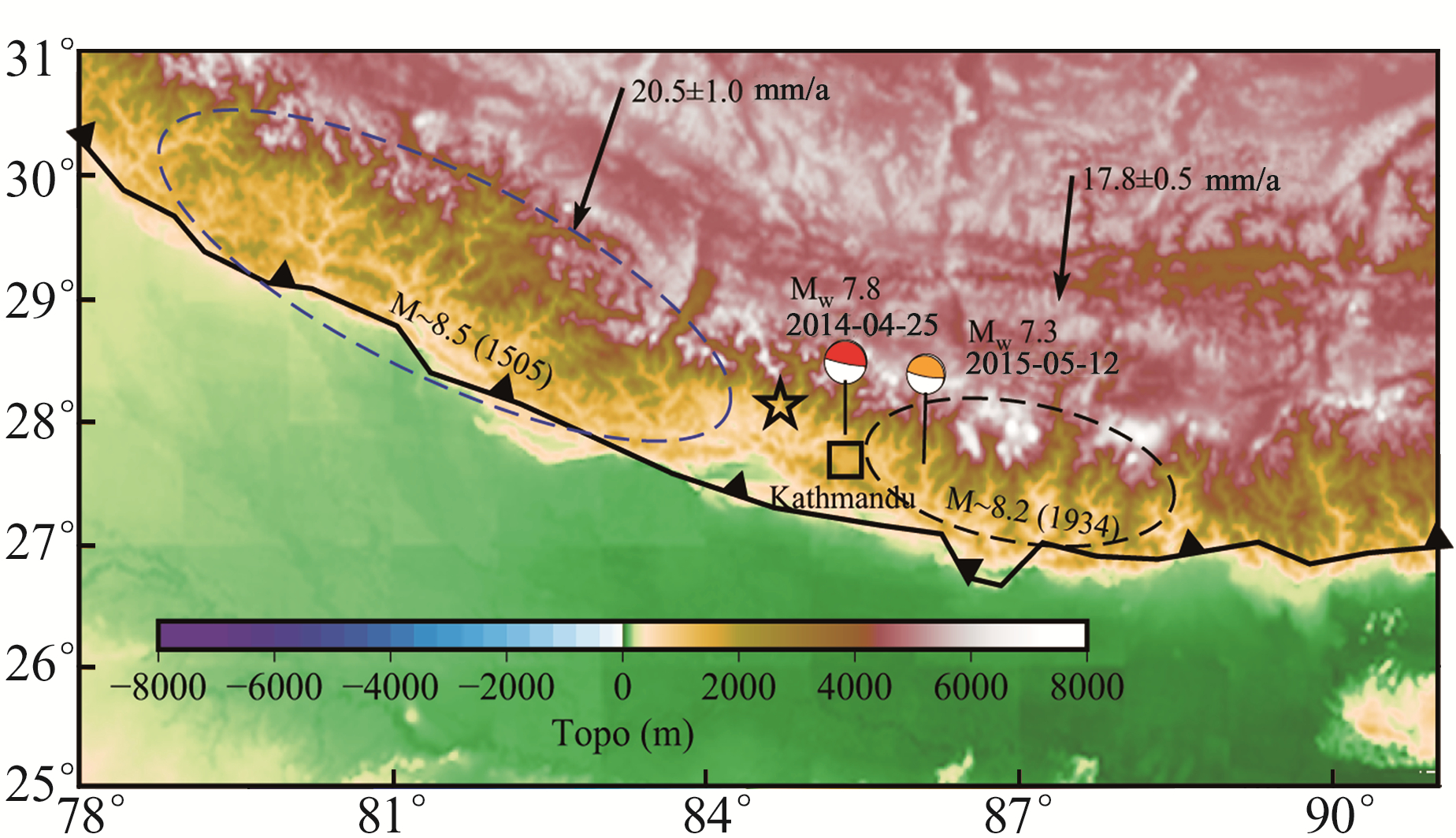
2 2015年尼泊尔地震的GPS反演 2.1 地震构造背景2015-04-25尼泊尔MW7.8地震发生在喜马拉雅山前缘,距加德满都80 km(图 1)。地震波得到的震源机制解表明,此事件是一次低角度逆冲断层滑移,近似于水平断层,向北倾斜约10°,震源深度约15 km,位于喜马拉雅俯冲带上(图 1,黑色五星为震中,由USGS给出)。大地测量数据的反演结果表明,在震间期,北印度洋板块向喜马拉雅俯冲速率约为2 cm/a,且几乎整个俯冲带浅部均处于闭锁状态[17]。在本次地震事件后发生多次余震,其中最大的为2015-05-12的MW7.3地震,位于加德满都东向,主震和最大余震的震源机制解来自GCMT。根据古地震资料结果[18-24],该次事件主震发生在1505年和1934年两个历史地震之间的空区上,两次M 7.5以上的历史地震分别用蓝色和黑色椭圆表示。
|
图 1 2015尼泊尔MW7.8地震的构造背景 Fig. 1 The tectonic background of 2015 Nepal MW7.8 earthquake |
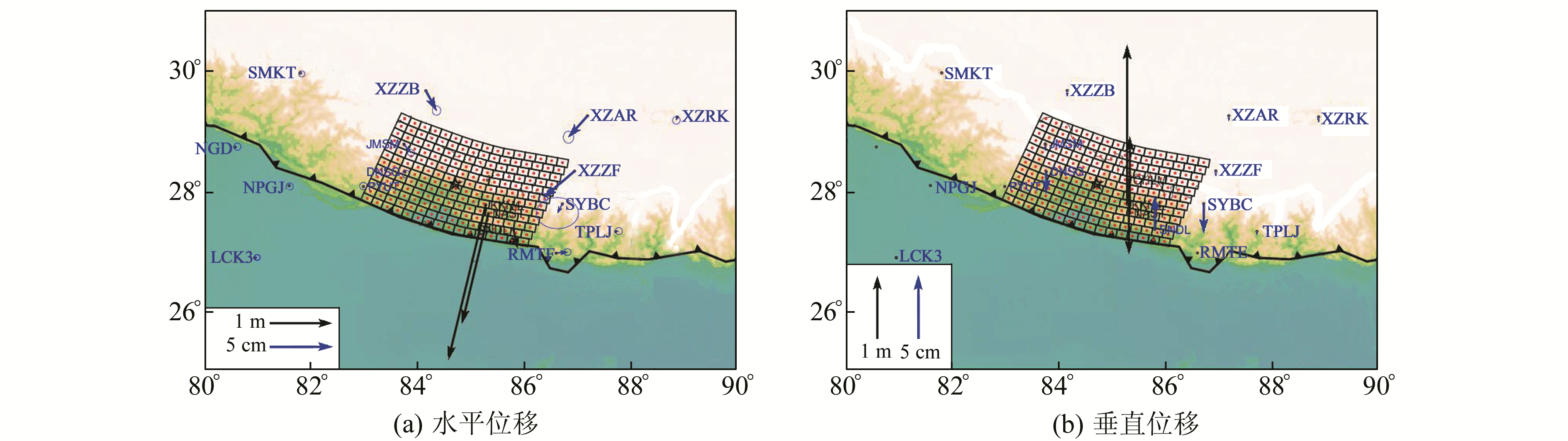
为了利用前文给出的MCMC方法得到2015年尼泊尔地震的同震滑移分布,采用文献[25]给出的19个GPS连续站观测的变形结果。GPS观测站大多位于高原一侧,且有超过10个站点位于震中附近。观测表明,最大变形发生在震中东南靠近板块边界的测站,水平位移为1.89 m,垂直位移为1.26 m(图 2)。整个GPS位移方向表明,该地震为一次逆冲滑移事件。
|
图 2 GPS观测的2015年尼泊尔地震同震变形和用于断层滑移反演的子断层模型 Fig. 2 The coseismic displacements of 2015 Nepal thrust event observed by GPS and the fault model discretized into 192 patches |
为了反演得到同震滑移分布,需要对逆冲断层进行离散。根据其他研究机构给出的震源机制解,本文将断层倾角设定为11°,走向根据板块边界线的变化给出[26](图 2)。将断层划分为16×12个子断层,每个子断层面积为20 km×15 km。如前所述,在反演时需要对断层面上的滑移进行平滑约束,这里选用Laplace算子构建约束方程。对于逆冲破裂事件,为了允许反演结果滑移能够达到地表,采用自由边界条件约束断层边界上的滑移[8]。为了避免不合理的反向滑移,反演时将滑移角限定在[45°,135°]。格林函数G采用球体分层位错理论模型[5]计算得到,地球模型选用PREM模型[27]。
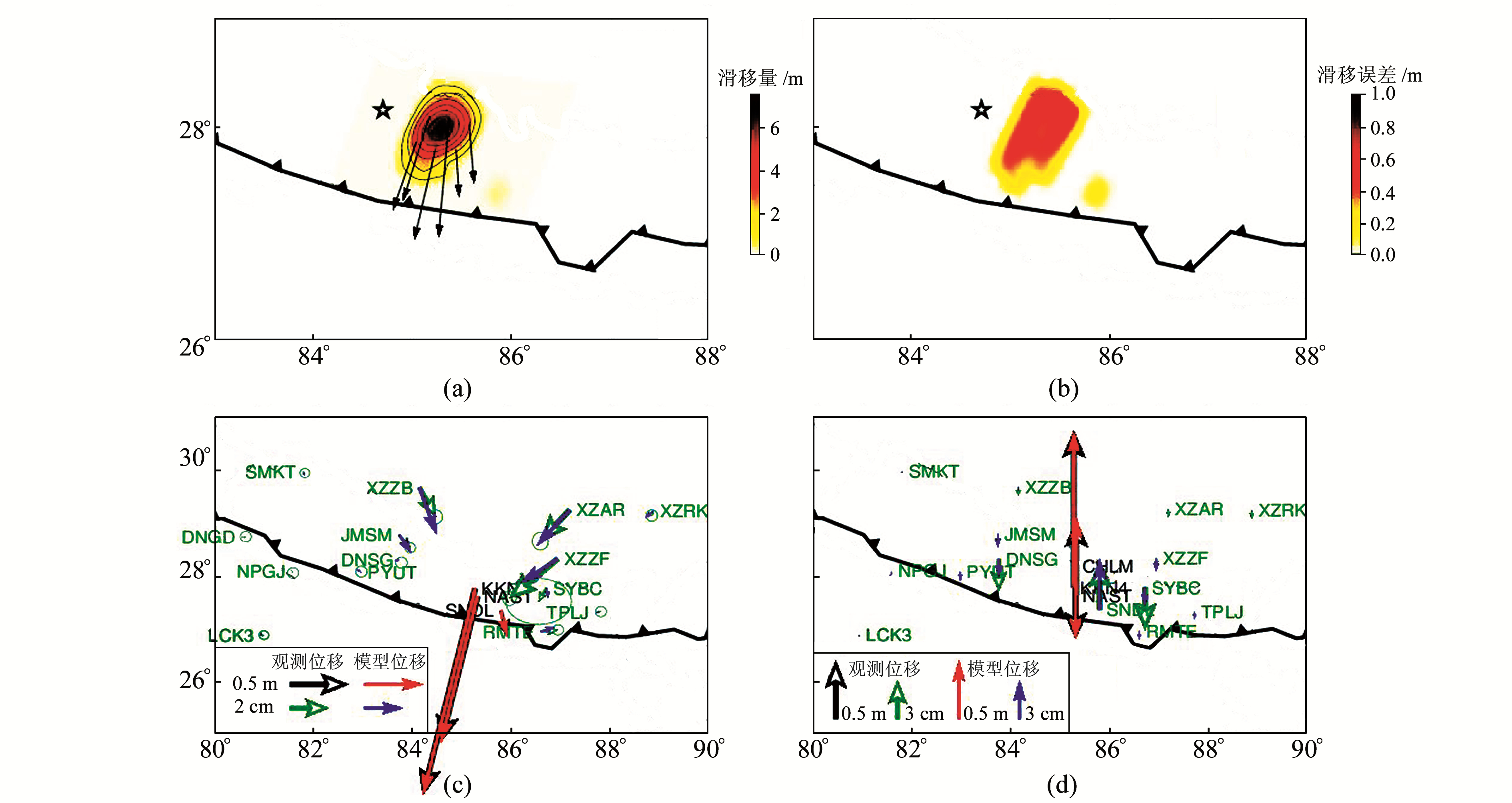
2.3 断层滑移反演结果利用改进的MCMC和GPS数据反演2015年尼泊尔地震的同震滑移分布。在反演过程中,Markov链的总长度由2×107个种子组成,燃烧阶段和采样阶段的长度均为1×107个种子,重采样的间隔为1 000。模拟退火过程中,初始温度设为100,终止温度为0.1,通过105步从初始温度冷却到终止温度。对状态空间重采样后,得到104个模型,将最大和最小各2.5%的模型去掉后,对剩余模型进行平均得到滑移模型及其误差,如图 3(a)、(b)所示。反演结果表明,滑移分布集中在震中东侧,最大滑移约7 m,滑移方向几乎垂直于走向,破裂未到地表。反演得到的地震矩为7.67×1020 Nm,相当于MW7.86,与其他研究结果较为一致。同震滑移的误差最大不超过0.7 m,较均匀地分布在滑移区域(图 3(b)),图 3(c)、(d)为模型拟合的位移与观测的GPS观测位移。
|
图 3 利用改进MCMC反演的2015年尼泊尔地震同震滑移分布及其反演误差 Fig. 3 The coseismic fault slip distribution and erros of the 2015 Nepal earthquake inverted by using improved MCMC approach |
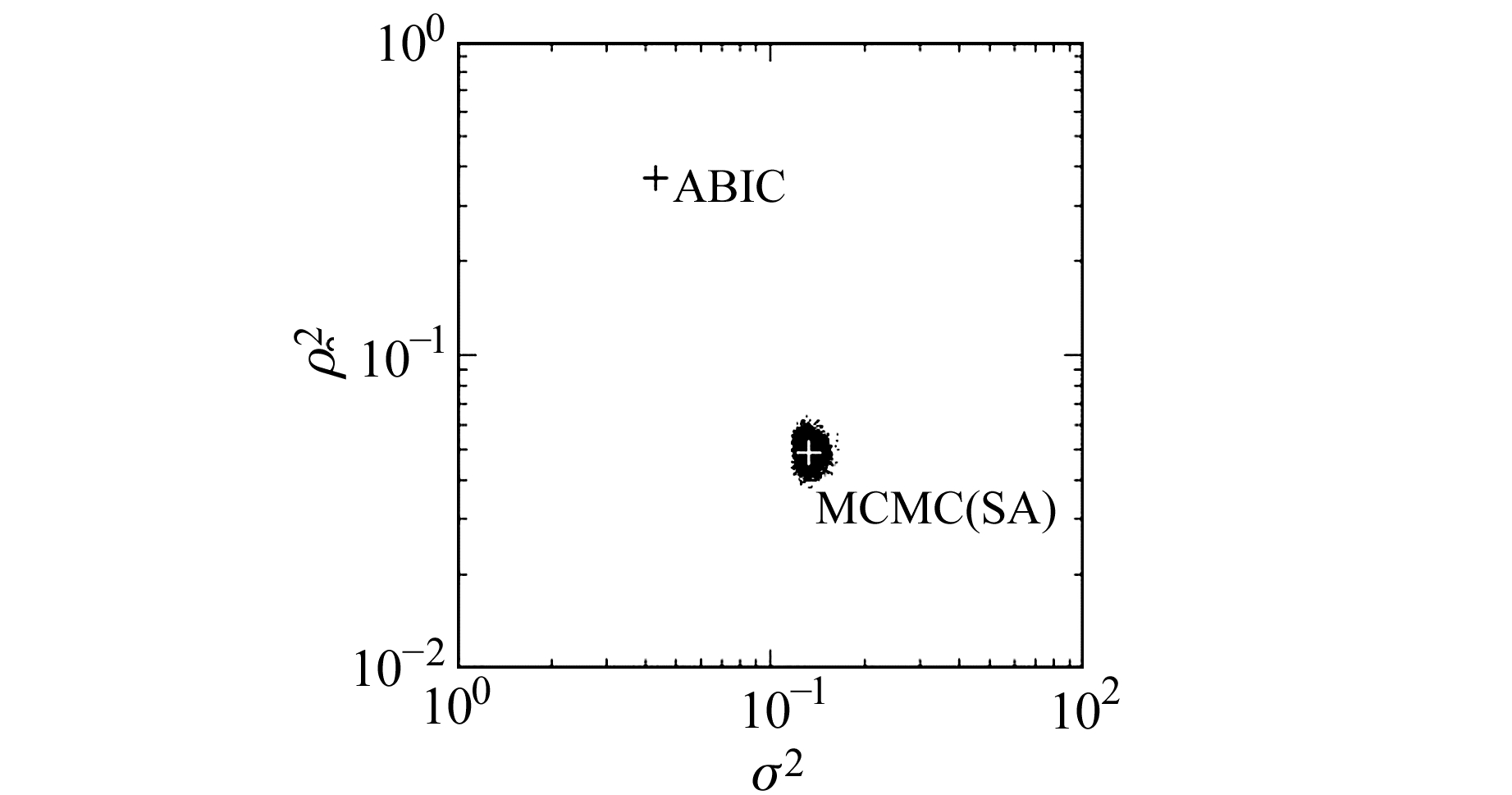
图 4给出了MCMC反演过程采样阶段对两个超参数σ2和ρ2的重采样分布(黑点),白色十字表示平均模型所在位置,黑色十字为ABIC方法得到的结果。可见,反演过程在燃烧阶段已经收敛,采样阶段在收敛区域内重采样,表明反演结果稳定可靠。与ABIC的结果相比,MCMC的ρ2更小,滑移模型更加平滑; σ2较大,数据的拟合程度不如ABIC方法。以上结果表明,在对断层面滑移分布施加非负约束后,MCMC方法能够使结果更平滑,更有利于解决过拟合的问题。
|
图 4 利用改进的MCMC方法反演滑移模型过程中,在(σ2,ρ2)二维空间的重采样分布 Fig. 4 The distribution of (σ2, ρ2) in 2-D space at the resampling stage during MCMC inversion for fault slip |
MCMC方法使得断层滑移分布更为平滑的同时,拟合数据的程度有所下降。尽管如此,比较观测和模型预测的GPS同震位移可知(图 3(c)、(d)),改进的MCMC方法得到的断层滑移模型仍然能够较好地解释GPS观测数据。故该方法在平滑断层滑移分布的同时,并未过多地损失观测数据的符合度。
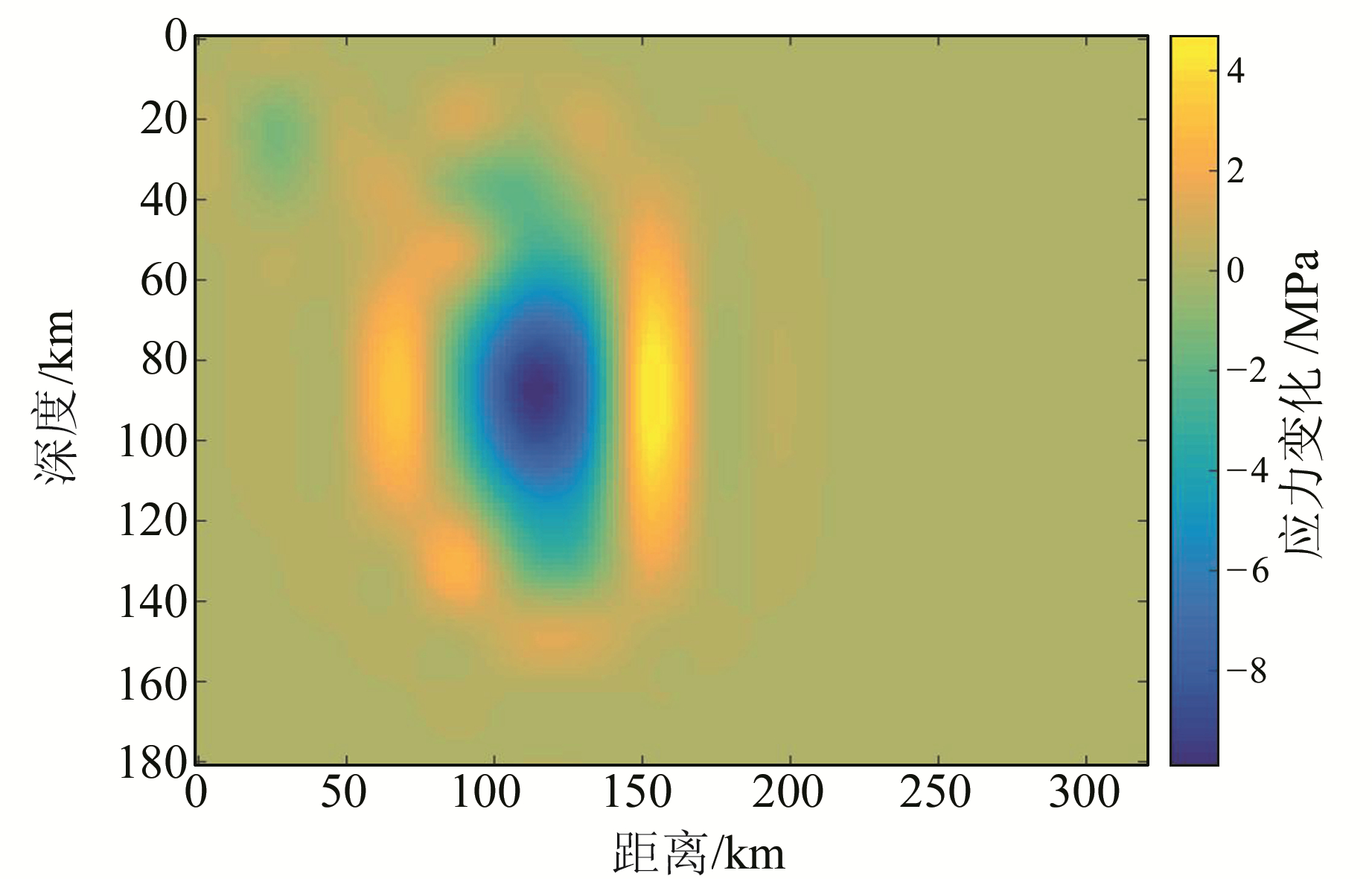
根据反演的断层滑移模型计算了逆倾向的应力变化,见图 5。断层上的应力变化主要以应力减小为主,集中在滑移较大的区域,最大超过8 MPa,为地震波辐射的主要区域。对断层面上的负应力取加权平均可得应力降:
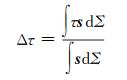
|
(22) |
|
图 5 利用同震滑移模型(图 3(a))得到的2015年尼泊尔地震应力变化,应力降为0.9 MPa Fig. 5 The stress change of 2015 Nepal earthquake calculated using coseismic fault slip model (Fig. 3(a)), the stress drop is 0.9 MPa |
式中,τ为应力变化; s为滑移量; dΣ为面积元。经计算,得到断层面上的应力降为0.9 MPa,水平较低,与前人得到的结论一致[28]。
利用GPS数据得到的平均滑移分布模型(图 3(a))与地震波、InSAR等资料得到的结果相似[24],不同的是本研究给出的滑移分布更加集中。与使用同样数据的研究结果[25]相比,本研究模型在沿走向的破裂尺度明显更小,差异在于使用的断层走向参数和反演方法不同。本研究的断层走向是沿板块边界变动,而其他学者采用的则是固定走向; 使用改进的MCMC方法得到的断层滑移模型是在采样阶段重采样后的平均模型,而文献[25]使用的则是ABIC方法。所有研究结果都表明,2015年尼泊尔地震的滑移分布在震中的东侧,主要原因是断层是由西向东破裂的,最大滑移发生在靠近加德满都附近。
图 6给出了同震滑移与喜马拉雅前缘的历史地震事件的关系。可知,本次地震事件发生在两次历史地震之间的空区上,破裂更靠近1934年M8.2地震区域。2015年地震的主要滑移区域与1505年M8.5地震区域仍然有空白未破裂的区域,未来有一定的危险性。

|
图 6 2015尼泊尔地震的同震滑移与构造背景 Fig. 6 The tectonic background of Himalaya and coseismic slip of the 2015 Nepal earthquake |
相比于解析的ABIC方法,MCMC方法是一种纯数值方法,需要经过大量采样计算,耗时较长。改进的MCMC方法能够加速Markov链的收敛速度。对于本文震例,采用改进的MCMC方法只需计算可接受的2×107个种子,而MCMC方法则需要至少2倍的种子数。
在利用MCMC方法的时候,可以选择单条长链串行计算,也可以选择多条短链并行计算。本文采用单条链,从一个初始状态经过燃烧和采样阶段得到重采样模型,最终取平均得到滑移分布。在计算过程中,初始状态和随机游走步长的选取同样影响收敛速度。当解空间的后验概率密度有多个峰值时,初始状态选择过于接近局部最小,需要耗费较长的时间跳出局部最小区域。随机游走步长若选取过小,则MCMC的效率过低; 反之,步长过大会跳过全局最优。本文实例中先给定一个接近ABIC方法确定的平滑因子,再利用非负最小二乘法反演得到滑移分布,然后将状态空间的零值加一个正常数作为初始状态。随机游走步长则通过大量测试考察结果的稳定性选择较为合理的步长。
另外,在时刻状态空间转移到时刻时,状态空间可以整体转移,也可以将状态空间中某一元素转移,其他元素保持不变,在下一时刻完成下一元素的转移,反复上述过程最后完成转移。后者的思想与Gibbs采样类似。实践证明,采用单一时刻对单一元素采样的方法计算效率更高。
4 结语本文利用改进的MCMC方法反演2015年尼泊尔地震的滑移分布,结果与其他手段得到的结果几乎一致,证明该方法有效可行。不同于其他反演方法,MCMC方法能够从统计上给出滑移模型的误差,约为滑移量的10%。用均方根定量估计ABIC和改进的MCMC两种方法的数据拟合误差,前者为2.5 mm,后者为4.1 mm。二维超参数空间的采样分布以及GPS的拟合结果表明,改进的MCMC方法在对滑移模型更加平滑的同时,并未损失过多的数据拟合度。
致谢: 与申文豪博士在应力降方面进行了讨论,与王振博士、Cambiotti在反演方法方面进行了讨论,在此一并致谢。
| [1] |
Okada Y. Surface Deformation Caused by Shear and Tensile Faults in a Half-Space[J]. Bull Seismol Soc Am, 1985, 75(4): 1 135-1 154
(  0) 0) |
| [2] |
Okubo S. Gravity and Potential Changes Due to Shear and Tensile Faults in a Half-Space[J]. J Geophys Res, 1992, 97(B5): 7 137-7 144 DOI:10.1029/92JB00178
(  0) 0) |
| [3] |
Wang R J, Lorenzo-Martín F, Roth F. PSGRN/PSCMP—A New Code for Calculating Co- and Post-Seismic Deformation, Geoid and Gravity Changes Based on the Viscoelastic-Gravitational Dislocation Theory[J]. Comput Geosci, 2006, 32(4): 527-541
(  0) 0) |
| [4] |
Sun W K, Okubo S. Surface Potential and Gravity Changes Due to Internal Dislocations in a Spherical Earth-I:Theory for a Point Dislocation[J]. Geophys J Int, 1993, 114(3): 569-592 DOI:10.1111/gji.1993.114.issue-3
(  0) 0) |
| [5] |
Sun W K, Okubo S, Vanicek P. Global Displacement Caused by Dislocations in a Realistic Earth Model[J]. J Geophs Res, 1996, 101(B4): 8 561-8 577 DOI:10.1029/95JB03536
(  0) 0) |
| [6] |
Yabuki T, Matsu'ura M. Geodetic Data Inversion Using a Bayesian Information Criterion for Spatial Distribution of Fault Slip[J]. Geophy J Int, 1992, 109(2): 363-375 DOI:10.1111/gji.1992.109.issue-2
(  0) 0) |
| [7] |
Jónsson S, Zebker H, Segall P, et al. Fault Slip Distribution of the 1999 MW7.1 Hector Mine, California, Earthquake, Estimated from Satellite Radar and GPS Measurements[J]. Bull Seismol Soc Am, 2002, 92(4): 1 377-1 389 DOI:10.1785/0120000922
(  0) 0) |
| [8] |
Zhou X, Cambiotti G, Sun W K, et al. The Coseismic Slip Distribution of a Shallow Subduction Fault Constrained by Prior Information: The Example of 2011 Tohoku (MW9.0) Megathrust Earthquake[J]. Geophys J Int, 2014, 199(2): 981-995 DOI:10.1093/gji/ggu310
(  0) 0) |
| [9] |
Matthews M V, Segall P. Estimation of Depth-Dependent Fault Slip from Measured Surface Deformation with Application to the 1906 San Francisco Earthquake[J]. J Geophys Res, 1993, 98(B7): 12 153-12 163 DOI:10.1029/93JB00440
(  0) 0) |
| [10] |
Hansen P C, O'Leary D P. The Use of the L-Curve in the Regularization of Discrete Ill-Posed Problems[J]. SIAM J Sci Comput, 1993, 14(6): 1 487-1 503 DOI:10.1137/0914086
(  0) 0) |
| [11] |
Golub G H, Heath M T, Wahba G. Generalized Cross-Validation as a Method for Choosing a Good Ridge Parameter[J]. Technometrics, 1979, 21(2): 215-223 DOI:10.1080/00401706.1979.10489751
(  0) 0) |
| [12] |
Lawson C, Hanson R. Solving Least-Squares Problems[M]. New Jersey: Prentice Hall, 1974
(  0) 0) |
| [13] |
Fukuda J, Johnson K M. A Fully Bayesian Inversion for Spatial Distribution of Fault Slip with Objective Smoothing[J]. Bull Seismol Soc Am, 2008, 98(3): 1 128-1 146 DOI:10.1785/0120070194
(  0) 0) |
| [14] |
Sun J B, Johnson K M, Cao Z Q, et al. Mechanical Constraints on Inversion of Coseismic Geodetic Data for Fault Slip and Geometry: Example from InSAR Observation of the 6 October 2008 MW6.3 Dangxiong-Yangyi(Tibet) Earthquake[J]. J Geophys Res, 2011, 116(B1)
(  0) 0) |
| [15] |
Fielding E J, Lundgren P R, Taymaz T, et al. Fault-Slip Source Models for the 2011 M7.1 Van Earthquake in Turkey from SAR Interferometry, Pixel Offset Tracking, GPS, and Seismic Waveform Analysis[J]. Seism Res Lett, 2013, 84(4): 579-593 DOI:10.1785/0220120164
(  0) 0) |
| [16] |
Akaike H. Likelihood and the Bayes Procedure, in Bayesian Statistics[M]. Valencia University Press, 1980
(  0) 0) |
| [17] |
Ader T, Avouac J P, Liu Z J, et al. Convergence Rate across the Nepal Himalaya and Interseismic Coupling on the Main Himalayan Thrust: Implications for Seismic Hazard[J]. J Geophys Res, 2012, 117(B4)
(  0) 0) |
| [18] |
Bilham R. Location and Magnitude of the 1833 Nepal Earthquake and Its Relation to the Rupture Zones of Contiguous Great Himalayan Earthquakes[J]. Curr Sci, 1995, 69(2): 101-128
(  0) 0) |
| [19] |
Ambraseys N N, Douglas J. Magnitude Calibration of North Indian Earthquakes[J]. Geophys J Int, 2004, 159(1): 165-206 DOI:10.1111/gji.2004.159.issue-1
(  0) 0) |
| [20] |
Lavé J, Yule D, Sapkota S, et al. Evidence for a Great Medieval Earthquake (Approximate to 1 100 AD) in the Central Himalayas, Nepal[J]. Science, 2005, 307(5 713): 1 302-1 305
(  0) 0) |
| [21] |
Kumar S, Wesnousky S G, Rockwell T K, et al. Paleoseismic Evidence of Great Surface-Rupture Earthquakes along the Indian Himalaya[J]. J Geophys Res, 2006, 111(B3)
(  0) 0) |
| [22] |
Mugnier J L, Gajurel A, Huyghe P, et al. Structural Interpretation of the Great Earthquakes of the Last Millennium in the Central Himalaya[J]. Earth Sci Rev, 2013, 127(1): 30-47
(  0) 0) |
| [23] |
Sapkota S N, Bollinger L, Klinger Y, et al. Primary Surface Ruptures of the Great Himalayan Earthquakes in 1934 and 1255[J]. Nature Geosci, 2013, 6(1): 71-76 DOI:10.1038/ngeo1669
(  0) 0) |
| [24] |
Avouac J P, Meng L, Wei S, et al. Lower Edge of Locked Main Himalayan Thrust Unzipped by the 2015 Gorkha Earthquake[J]. Nature Geosci, 2015, 8(9): 708-711 DOI:10.1038/ngeo2518
(  0) 0) |
| [25] |
苏小宁, 王振, 孟国杰, 等. GPS观测的2015年尼泊尔MS8.1级地震震前应变积累及同震变形特征[J]. 科学通报, 2015, 60(22): 2 115-2 123 (Su Xiaoning, Wang Zhen, Meng Guojie, et al. Pre-Seismic Strain Accumulation and Co-Seismic Deformation of the 2015 Nepal MS8.1 Earthquake Observed by GPS[J]. Chin Sci Bull, 2015, 60(22): 2 115-2 123)
(  0) 0) |
| [26] |
Bird P. An Updated Digital Model of Plate Boundaries[J]. Geochemistry, Geophysics, Geosystems, 2003, 4(3)
(  0) 0) |
| [27] |
Dziewonski A M, Anderson D L. Preliminary Reference Earth Model[J]. Phys Earth Planet Inter, 1981, 25(4): 297-356 DOI:10.1016/0031-9201(81)90046-7
(  0) 0) |
| [28] |
Kanamori H, Anderson D L. Theoretical Basis of Some Empirical Relations in Seismology[J]. Bull Seismol Soc Am, 1975, 65(5): 1 073-1 095
(  0) 0) |
 2017, Vol. 37
2017, Vol. 37

