2. 流域生态与地理环境监测国家测绘地理信息局重点实验室,南昌市广兰大道418号,330013;
3. 江西省数字国土重点实验室,南昌市广兰大道418号,330013
在测量过程中,受设备、观测者及环境等影响,会产生不确定性,使观测值在真值左右波动[1-2]。不确定性包含偶然误差、系统误差、粗差、数值和概念误差、可度量和不可度量误差[3]。不确定度是不确定性的度量,可以用方差、均方差、误差区间、误差椭圆等表示[4]。
文献[4-7]研究了不确定性和不确定度基础理论,文献[8-10]对不确定度的估计和应用作了研究。文献[11]对系数矩阵和观测向量同时存在不确定性的问题建立不确定性min-max平差准则,先利用奇异值分解(SVD)得到中间参数的方程,再解方程得到未知参数估值。特别地,对系数矩阵部分列存在不确定性的部分不确定性min-max平差准则,先用QR分解将其转换成一般形式,再用SVD和解方程得未知参数估值。文献[12]针对不确定性min-max平差准则,提出一种基于线性矩阵不等式(LMI)的参数估计方法。文献[5]使用不确定性min-max平差准则建立不确定性平差模型,而对于SVD后得到的中间参数方程,采用迭代算法得到未知参数估值。文献[13]给出部分不确定性平差模型,同样采用SVD后的迭代算法求解中间参数。整个求解过程过于复杂,且没有讨论迭代不收敛时的求解方法。
为提高部分不确定性平差模型的解算效率,本文在不使用QR分解和SVD的基础上,直接采用迭代算法进行求解,并讨论迭代不收敛时的求解方法。
1 平差模型及准则设系数矩阵为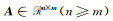
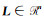
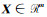

|
(1) |
式中,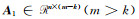

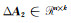
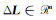
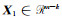
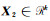
针对式(1),采用min-max准则[11, 13]进行解算:
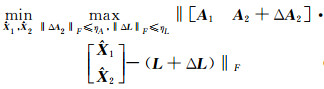
|
(2) |
式中,符号“^”表示最优估值。该平差准则分为max(·)和min(·)内外两层,内层的目标函数max(·)表示在系数矩阵子块A2和观测向量L分别受有界不确定性ΔA2和ΔL干扰情况下,得到未知参数时,残差的最大不确定性;外层的目标函数min(·)表示使参数解中的不确定性最小化。
将ΔA2和ΔL看成自变量,根据范数性质,其极大值点就是最大值点,设为(ΔA20,ΔL0)。当[13]
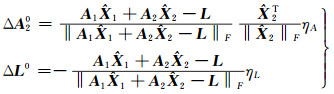
|
(3) |
时,max(·)取得极大值,亦即最大值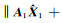
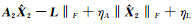
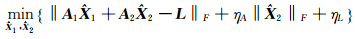
|
(4) |
针对平差准则(4),文献[11]先对系数矩阵A用QR分解,将其转化为一般形式;再对目标函数求导,得到未知参数估计式;然后用SVD得到中间参数方程,并解出唯一正根;最后将其代入未知参数估计式,得到未知参数估值,简称QR分解-SVD-解方程法。而文献[13]直接对目标函数求导,对A进行SVD,采用迭代算法解出中间参数估值,简称SVD-迭代算法。以上方法解算过程都较为复杂,不易实现。本文提出一种更为简单的方法,直接利用迭代算法解算未知参数估值。
2 模型解算 2.1 直接迭代算法当迭代算法收敛时,可直接采用迭代算法求解平差准则(4)。令目标函数为:
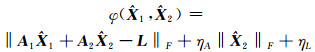
|
(5) |
问题(4)转变为求解含有F-范数的二元函数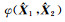
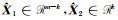

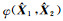
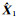
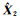
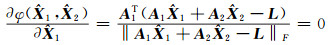
|
(6) |
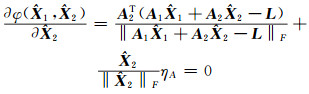
|
(7) |
联合式(6)和式(7),并参考文献[13],先讨论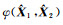
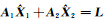
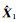
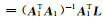
进一步讨论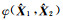

|
由式(6),得:
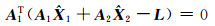
|
(8) |
式中,A1为列满秩矩阵,从而N11为满秩矩阵,所以N11的逆矩阵一定存在且唯一。由式(8)得:
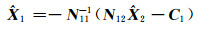
|
(9) |
由式(7)得:
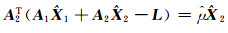
|
(10) |
式中,
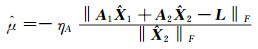
|
(11) |
将式(9)代入式(10),整理得:

|
(12) |
式中,Ik为k阶单位矩阵。式(12)两端都含有未知参数估值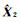
部分不确定性平差模型的迭代算法步骤为:
1) 给定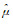
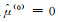
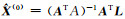
2) 用获得的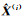
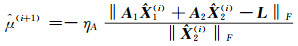
|
代入式(12),得:
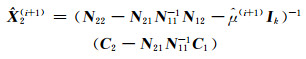
|
再将其代入式(9),得:
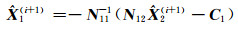
|
3) 重复步骤2),直到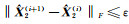
当迭代不收敛时,本文对QR分解-SVD-解方程法进行讨论[11]。对系数矩阵A进行QR分解:
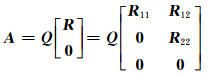
|
(13) |
式中,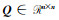
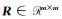
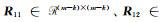
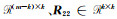
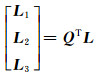
|
(14) |
式中,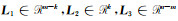

|
(15) |
在式(15)中,根据范数性质,若解算出未知参数估值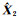
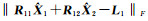
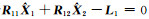
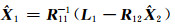
|
(16) |
令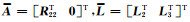
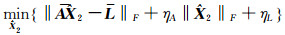
|
(17) |
对A进行SVD:
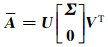
|
(18) |
式中,
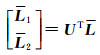
|
(19) |
式中,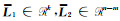
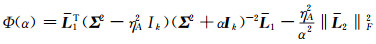
|
(20) |
并令
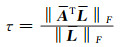
|
(21) |
设L2≠0,若ηA≥τ,则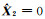
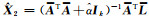

在以下算例中,所用计算机CPU为Intel(R) Core(TM) i7-6500U,主频为2.50 GHz,内存为8 GB;采用软件Matlab R2012a(7.14.0.739),64 bit。系统误差为常数s,随机误差由函数normrnd产生,期望为μ、标准差为σ。简记DI为本文提出的直接迭代算法,QSE为QR分解-SVD-解方程法,SI为SVD-迭代算法。取ε=10-12。
3.1 直线拟合算例用直线方程y=5.813 2-0.601 7x生成一组10个不含误差的点(xi,yi),模拟真值见表 1。再向其中同时加入系统误差(s=-0.10)和随机误差(μ=0,σ=0.41),并满足ηA=ηL=1.30,得到同时含有这两种误差的系数矩阵A和观测向量L:
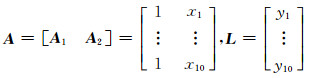
|
|
|
表 1 直线拟合的模拟真值 Tab. 1 Simulation data of straight line fitting |
共模拟1 000次。采用DI、QSE和SI分别进行参数估计,得到DI和SI的迭代次数以及3种算法的参数估值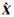

|
图 1 DI和SI直线拟合的迭代次数 Fig. 1 Iterations of straight line fitting by DI and SI |
|
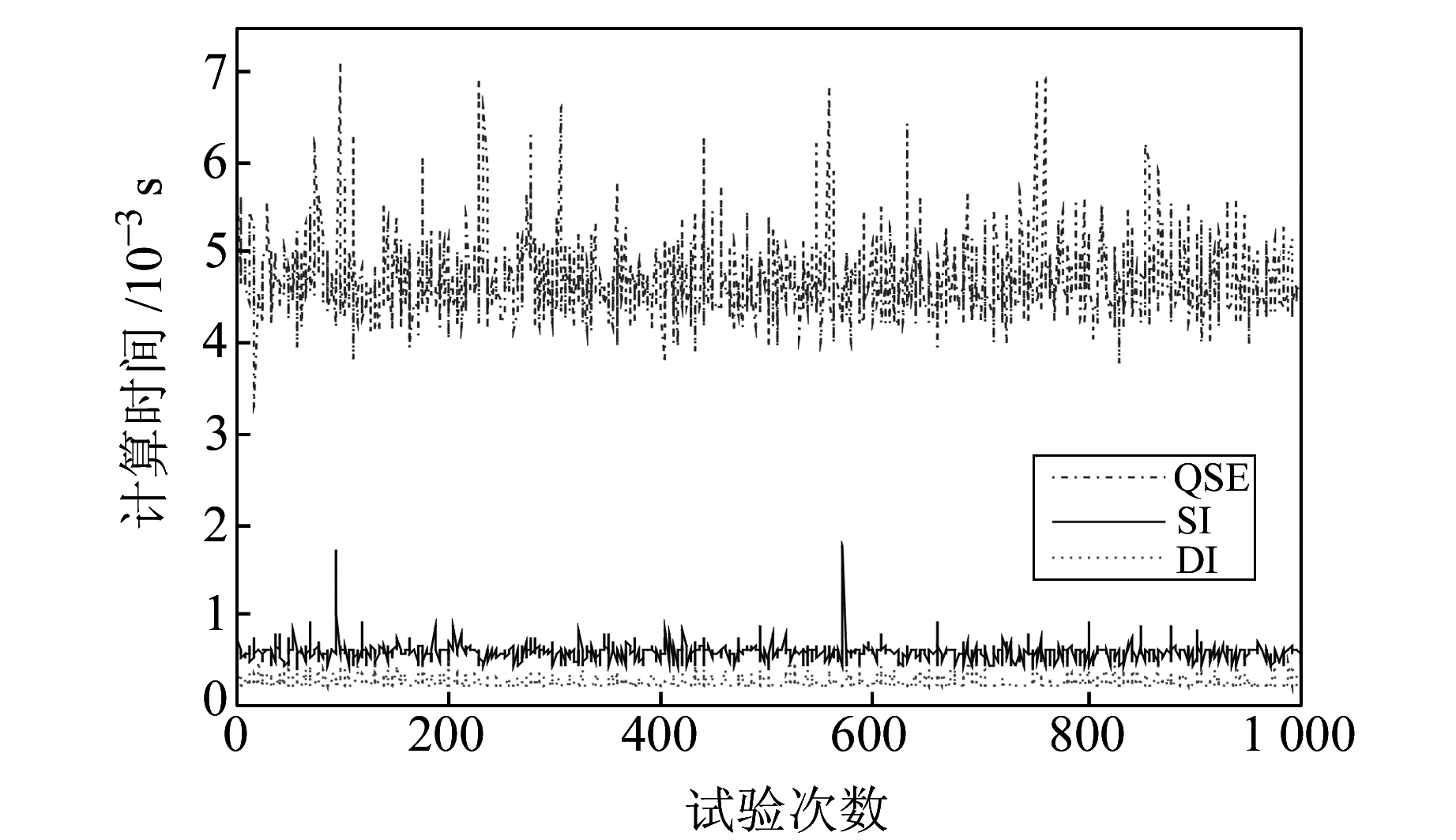
图 2 3种直线拟合算法的计算时间 Fig. 2 Computation time of straight line fitting by three algorithms |
|
|
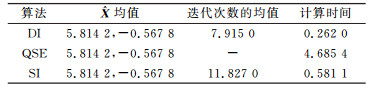
表 2 3种直线拟合算法的结果 Tab. 2 The results of straight line fitting by three algorithms |
从表 2第2栏看出,DI得到的未知参数估值与另外两种算法一致,说明DI是正确可行的。
图 1统计了DI和SI的迭代次数,DI每次计算的迭代次数都要比SI少。表 2第3栏列出DI和SI计算1 000次的平均迭代次数,DI的迭代效率比SI提高约33.08%。图 2统计了3种算法每次计算的时间,DI每次都是最少的。表 2第4栏还列出它们计算1 000次的总时间,DI总的时间效率较QSE提高约94.41%,较SI提高约54.91%。分析可知,DI的解算效率比另外两种算法都有明显提高。
从图 1知,DI总体迭代次数的波动范围比SI小,说明DI的稳定性比SI好;从图 2知,DI计算时间的波动范围比QSE和SI都要窄,说明DI计算时间的稳定性也更好。
3.2 平面坐标转换算例假设平面坐标转换的函数模型为:
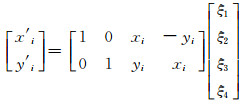
|
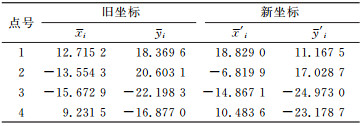
给定转换参数真值[3.708 6 -5.216 7 0.988 2 -0.139 1]T,及4个不含误差的旧坐标点(xi,yi),由此生成4个新坐标点(xi′,yi′),见表 3。给新旧坐标同时加入系统误差(s=-0.05)和随机误差(μ=0,σ逐次增大),使得不确定度ηA=ηL的初始值为0.40,步长为0.40,终止值为3.60,共产生9组同时含有这两种误差的新旧坐标,得到系数矩阵A和观测向量L:

|
|
|
表 3 新旧坐标的模拟真值 Tab. 3 Simulation data of target and source coordinates |
每组模拟1 000次,采用DI、QSE和SI分别对其进行参数估计,统计DI和SI迭代次数的均值以及3种算法的计算时间,见图 3和图 4。
|
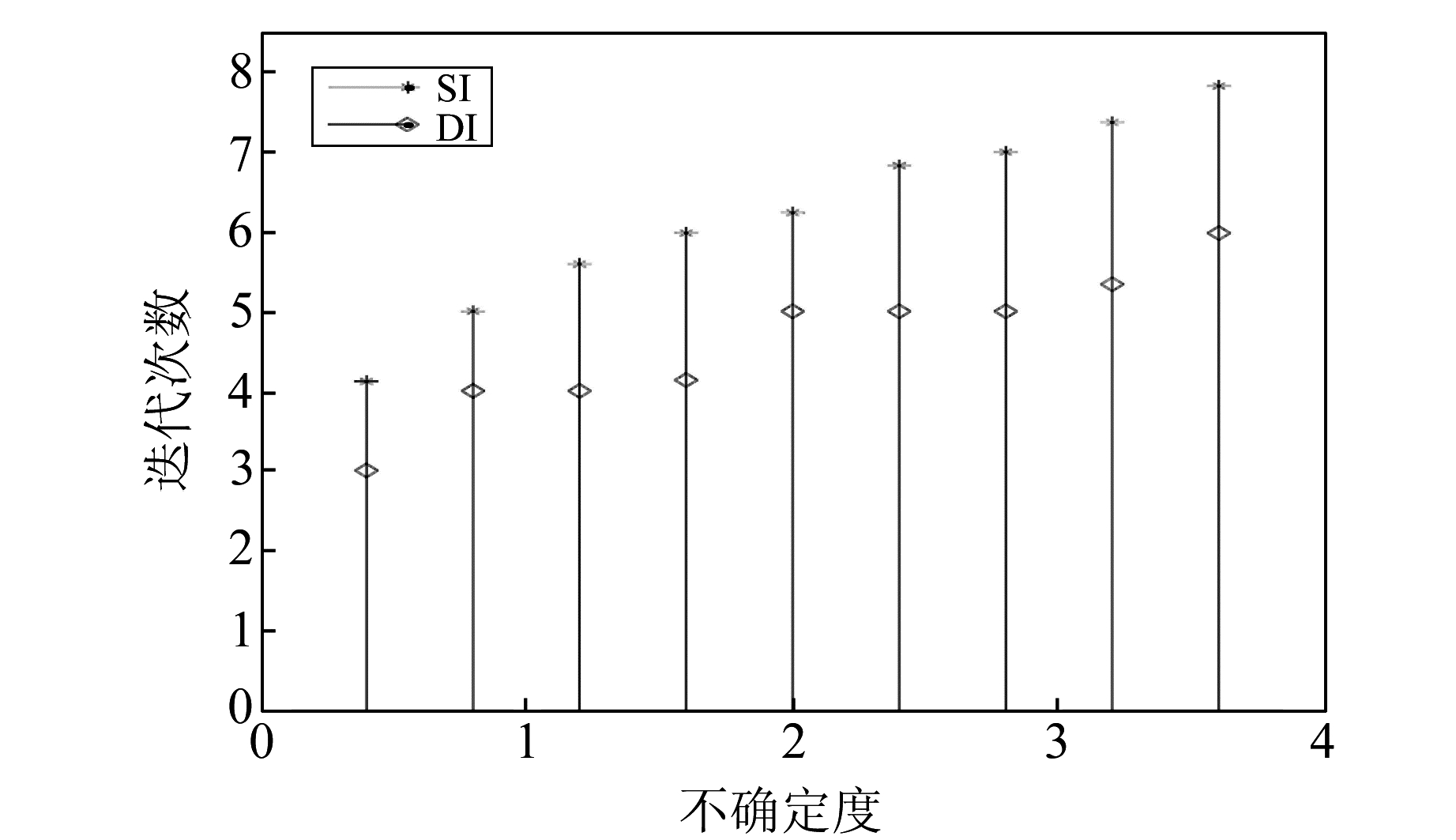
图 3 DI和SI坐标转换的迭代次数 Fig. 3 Iterations of coordinate transformation by DI and SI |
|
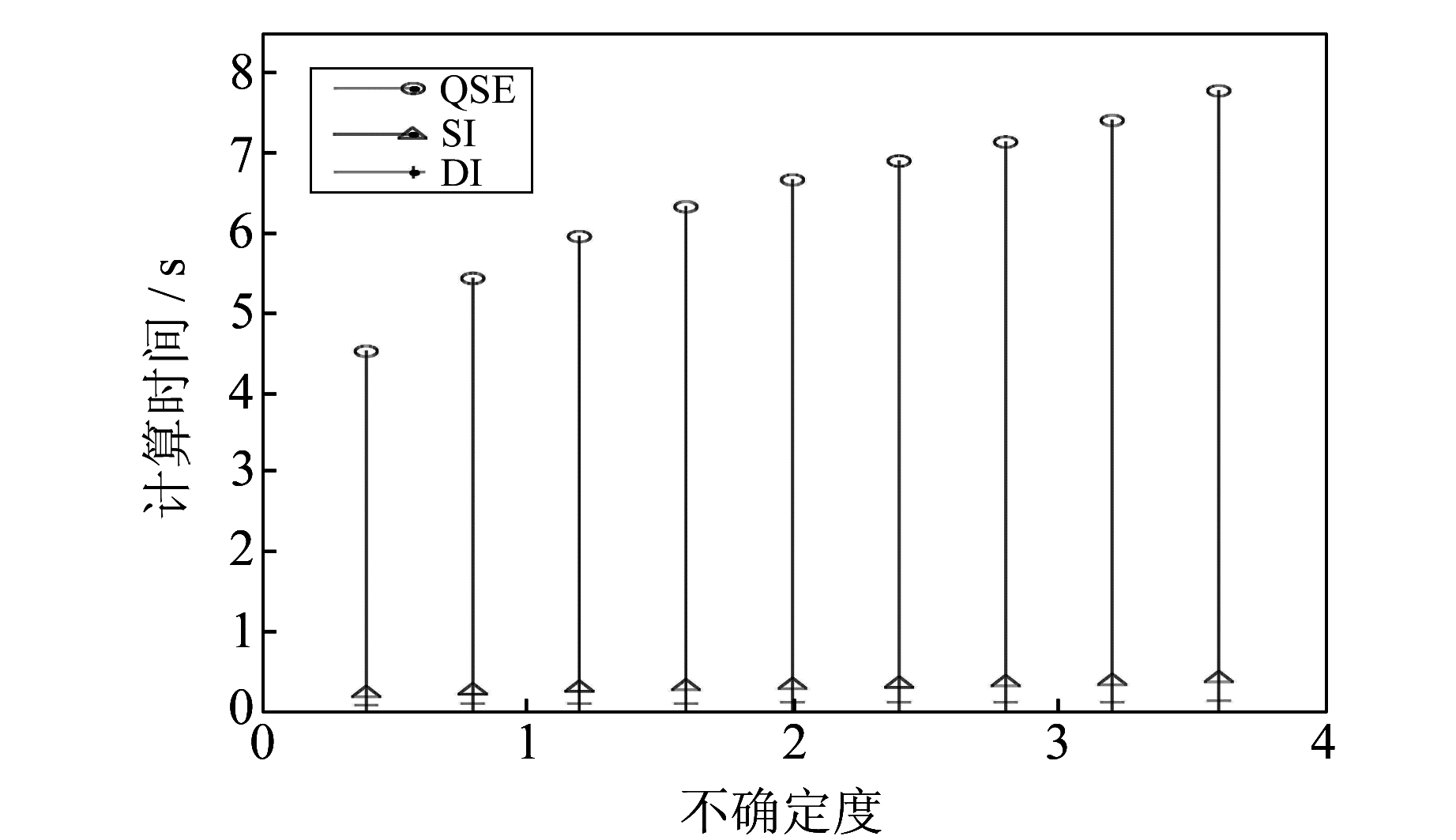
图 4 3种坐标转换算法的计算时间 Fig. 4 Computation time of coordinate transformation by three algorithms |
从图 3可以看出,随着不确定度的增加,DI和SI的迭代次数也有不同程度的增加,且DI的迭代次数较少;它们的均值分别为约4.607 8和6.220 2,方差分别为约0.718 0和1.242 3,DI迭代次数的均值和方差都较小,说明DI较SI迭代效率较高,且更为稳定。
观察图 4,随着不确定度的逐次增加,DI、QSE和SI的计算时间也随之增加。它们计算时间的均值分别为约0.103 7、6.456 3和0.328 2,方差分别为约0.000 3、0.939 1和0.003 2。显然,DI计算时间的均值和方差都是最小的,较其他两种算法计算的时间效率最高,且最为稳定。
4 结语本文推导了部分不确定性平差模型的直接迭代算法,并讨论了迭代不收敛时的算法。得到几点结论:1)直接迭代算法是正确可行的,且概念简单,易于实现。2)直接迭代算法有着更快的收敛速度、更高的解算效率、更好的稳定性。3)当迭代不收敛时,迭代算法会失效,此时可用QR分解-SVD-解方程法解算,但过程较为复杂,解算效率较低。
本文主要是从解算效率方面进行探讨,而系数矩阵和观测向量不确定度的获取以及部分不确定性平差模型的应用等,还需进一步研究。
| [1] |
王新洲, 史文中. 极大可能性估计[J]. 测绘学报, 2003, 32(3): 193-197 (Wang Xinzhou, Shi Wenzhong. Maximum Possibility Estimation[J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(3): 193-197 DOI:10.3321/j.issn:1001-1595.2003.03.002)
(  0) 0) |
| [2] |
陈伟.最小不确定度估计理论及其应用[D].武汉: 武汉大学, 2005 (Chen Wei. Least Uncertainty Estimation Theory with Application[D]. Wuhan: Wuhan University, 2005) http://cdmd.cnki.com.cn/article/cdmd-10486-2006032055.htm
(  0) 0) |
| [3] |
武汉大学测绘学院测量平差学科组. 误差理论与测量平差基础[M]. 武汉: 武汉大学出版社, 2009 (Surveying Adjustment Group of School of Geodesy and Geomatics of Wuhan University. Error Theory and Foundation of Surveying Adjustment[M]. Wuhan: Wuhan University Press, 2009)
(  0) 0) |
| [4] |
杨元喜. 卫星导航的不确定性、不确定度与精度若干注记[J]. 测绘学报, 2012, 41(5): 646-650 (Yang Yuanxi. Some Notes on Uncertainty, Uncertainty Measure and Accuracy in Satellite Navigation[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 646-650)
(  0) 0) |
| [5] |
宋迎春, 谢雪梅, 陈晓林. 不确定性平差模型的平差准则与解算方法[J]. 测绘学报, 2015, 44(2): 135-141 (Song Yingchun, Xie Xuemei, Chen Xiaolin. Adjustment Criterion and Algorithm in Adjustment Model with Uncertainty[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(2): 135-141)
(  0) 0) |
| [6] |
陶本藻. GIS质量控制中不确定度理论[J]. 测绘学院学报, 2000, 17(4): 235-238 (Tao Benzao. Basic Theory of Uncertainty of Quality Control in GIS[J]. Journal of Institute of Surveying and Mapping, 2000, 17(4): 235-238 DOI:10.3969/j.issn.1673-6338.2000.04.001)
(  0) 0) |
| [7] |
杨元喜. 关于"新的点位误差度量"的讨论[J]. 测绘学报, 2009, 38(3): 280-282 (Yang Yuanxi. Discussion on "A New Measure of Positional Error"[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(3): 280-282 DOI:10.3321/j.issn:1001-1595.2009.03.015)
(  0) 0) |
| [8] |
陶本藻. 精确度和不确定度估计及应用[J]. 勘察科学技术, 2003(5): 24-27 (Tao Benzao. Estimation of Accuracy and Uncertainty and Its Application[J]. Site Investigation and Technology, 2003(5): 24-27 DOI:10.3969/j.issn.1001-3946.2003.05.009)
(  0) 0) |
| [9] |
邹永刚, 翟京生, 刘雁春, 等. 利用不确定度的海底数字高程模型构建[J]. 武汉大学学报:信息科学版, 2011, 36(8): 964-968 (Zou Yonggang, Zhai Jingsheng, Liu Yanchun, et al. Seabed DEM Construction Based on Uncertainty[J]. Geomatics and Information Science of Wuhan University, 2011, 36(8): 964-968)
(  0) 0) |
| [10] |
陈伟, 张践. 最小不确定度估计及其在测量数据处理中的应用[J]. 测绘通报, 2013(1): 16-18 (Chen Wei, Zhang Jian. Least Uncertainty Estimation Theory and Its Applications in Survey Data Processing[J]. Bulletin of Surveying and Mapping, 2013(1): 16-18)
(  0) 0) |
| [11] |
Chandrasekaran S, Golub G H, Gu M, et al. Parameter Estimation in the Presence of Bounded Data Uncertainties[J]. SIAM Journal on Matrix Analysis & Applications, 1998, 19(1): 235-252
(  0) 0) |
| [12] |
杨智慧, 毛剑琴, 魏可惠. 基于LMI的具有一类不确定性数据的参数估计[J]. 北京航空航天大学学报, 2000, 26(4): 481-484 (Yang Zhihui, Mao Jianqin, Wei Kehui. Parameter Estimation Based on LMI with Bounded Data Uncertainties[J]. Journal of Beijing University of Aeronautics and Astronautics, 2000, 26(4): 481-484 DOI:10.3969/j.issn.1001-5965.2000.04.029)
(  0) 0) |
| [13] |
陈晓林, 宋迎春, 邹渤. 部分有界不确定性数据平差方法[J]. 大地测量与地球动力学, 2015, 35(1): 118-121 (Chen Xiaolin, Song Yingchun, Zou Bo. Adjustment of Part Bounded Uncertain Data[J]. Journal of Geodesy and Goedynamics, 2015, 35(1): 118-121)
(  0) 0) |
2. Key Laboratory of Watershed Ecology and Geographical Environment Monitoring, NASMG, 418 Guanglan Road, Nanchang 330013, China;
3. Jiangxi Province Key Lab for Digital Land, 418 Guanglan Road, Nanchang 330013, China
 2017, Vol. 37
2017, Vol. 37