2. 重庆大学土木工程学院,重庆市沙正街174号,400044
球标靶特征提取主要是获取球心坐标和半径,其中最常用的方法是Shakaji[1]提出的最小二乘方法(LS),其利用球面方程拟合获取球心的位置, 但没有考虑观测方程的系数误差。鲁铁定等[2]提出基于整体最小二乘(TLS)的球标靶定位方法,在一定程度上提高了定位精度,但没有考虑入射角角度对球面点云点位精度的影响。陈玮娴等[3]在文献[2]的基础上,考虑入射角角度变化对点位精度的影响,并利用加权整体最小二乘(WTLS)方法,提高了球标靶定位的准确度。官云兰等[4]提出了稳健的地面扫描球标靶定位方法,具有一定的稳健性,但定位精度较加权整体最小二乘低。王乐洋等[5]考虑权因数,提出了利用稳健加权整体最小二乘(RWTLS)方法,定位精度有所提高,但是相对加权整体最小二乘方法改进较小。
本文基于球截面圆心法线必过球心的性质,构造球心到球截面圆心法线距离平方和的目标函数,以此目标函数最小为条件, 对球标靶特征提取方法进行研究,并根据入射角对点位精度的影响对截面圆定义权重,设定截面圆的约束条件,提出基于球体几何关系的球标靶特征提取算法(geometrical relationship-weighed least square,GR-WLS)。
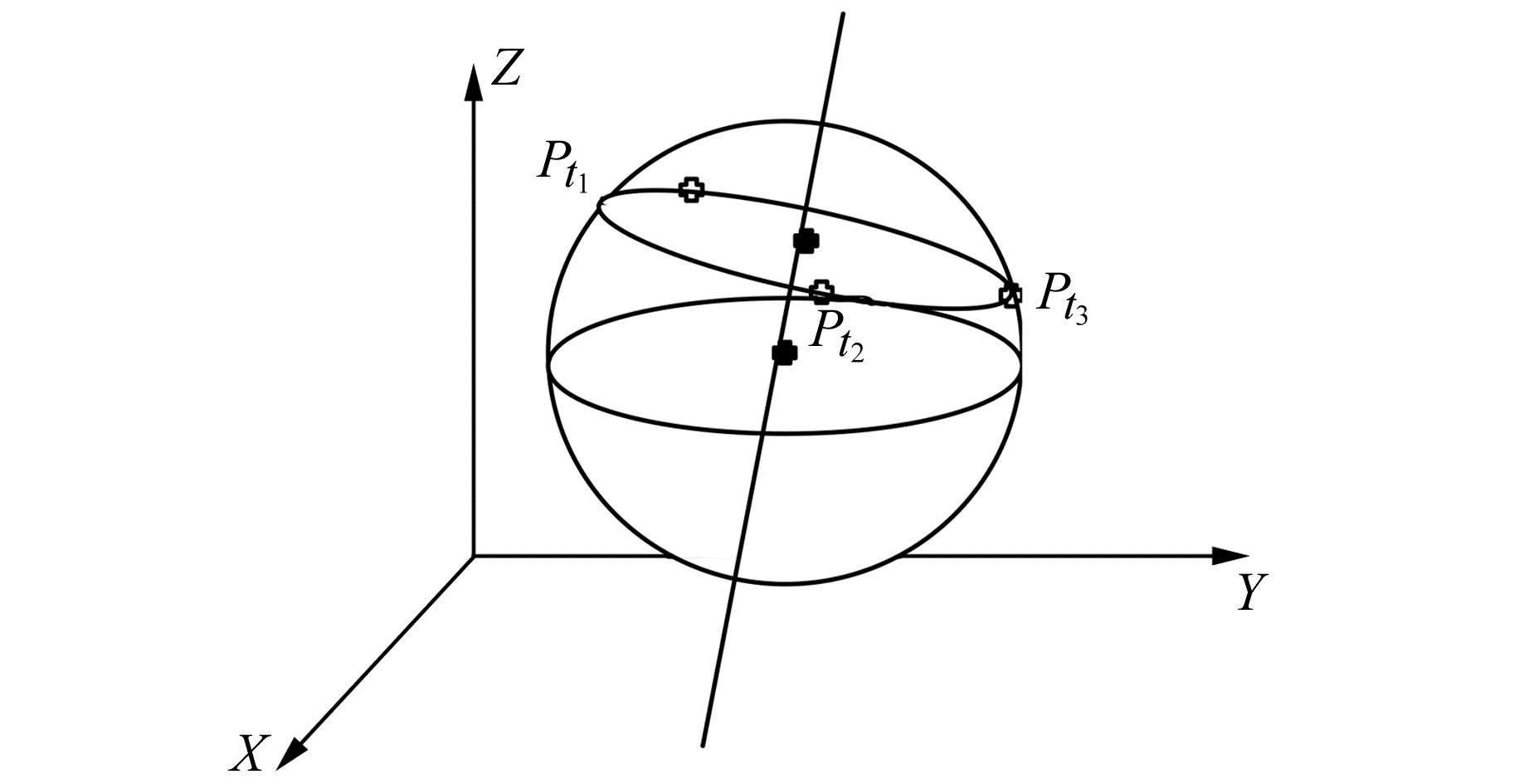
1 基于球体几何关系的球标靶特征提取算法球面上任意3点可构建一个平面,该平面与球体相交,相交曲线为圆,即为截面圆,该截面圆圆心与球心的连线垂直于截面圆所在平面[6]。
1.1 球体截面圆的几何关系设球面上任意3点Pt1、Pt2、Pt3(图 1),坐标分别为(x1, y1, z1)、(x2, y2, z2)、(x3, y3, z3), 过该3点构成一个截面圆,其圆心坐标为(acircle, bcircle, ccircle),半径为rcircle,根据文献[7]计算其圆心坐标和过圆心的截面圆方程。
|
图 1 截面圆几何关系 Fig. 1 Geometrical relationship of section circle |
激光反射强度与入射角度和扫描距离有关,入射角度越小,距离越近,扫描点的点位精度越高,参与拟合的权重也应越大[8-9]。设αi为入射角,si为扫描距离,则:
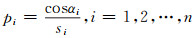
|
(1) |

|
(2) |
式中,pi为扫描点的权重,pcirclej为截面圆权重,pi1、pi2、pi3为任意3个构建截面圆的扫描点权重。
1.3 截面圆的约束条件已知扫描点云的扫描间隔Δ,扫描球标靶的半径为r,用最小二乘方法求得球标靶球心坐标(a, b, c),约束条件如下[10]:
1) 截面三角形为锐角三角形;
2) 截面三角形的边长大于3Δ;
3) 截面圆的半径小于球体半径r;
4) 点(a, b, c)到过截面圆圆心法线的距离小于3Δ。
1.4 方法步骤1) 球标靶扫描点云Cloud,数量n,由LS计算球心坐标(a0, b0, c0)和半径r0作为初始值。设置构建的截面圆个数count(根据模拟试验,选取点云数量1/3最为合适),定义变量j=1。
2) 从点云Cloud中任选3个不同点构建截面圆,判断该截面圆是否符合截面圆约束条件。若是则按文献[7]计算截面圆心法线方程,存入circlej,按式(3)、(4)计算截面圆的权Pciclej;否则,重新选择3点。
3) j加1,判断j是否大于count,若是则执行下一步,否则返回第2)步。
4) 以(a0, b0, c0)为正方体几何中心,以边长3Δ构建正方体,确定球心待选区域D。以0.01 mm为最小刻度,从X、Y、Z三个方向划分,获取所有节点Q, k为节点个数,定义变量i=1。
5) 选择Q中第i个节点poii,计算节点poii与步骤2)计算的所有截面圆心法线的有效距离之和存入dcircle1(节点到截面圆心法线的距离与截面圆权倒数之积为有效距离)。
6) 令i=i+1,判断i是否大于k。若是则输出dcircl1值最小的对应待选点,即为需要求取的圆心坐标(a, b, c),否则返回第5)步。
7) 以(a, b, c)为球心,计算所有扫描点到该点的距离,均值为半径r。拟合球面,计算扫描点到该球面的距离disti, 利用式(4)计算球面的拟合精度σCloud,检验球面对点云的拟合效果[6]:
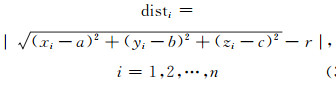
|
(3) |
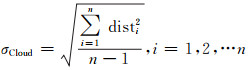
|
(4) |
为了验证本文算法(GR-WLS)的准确性和稳健性, 2016-09-27在重庆市地质矿产研究院用Leica ScanStation C10扫描仪对球形标靶进行扫描。具体实验步骤如下:
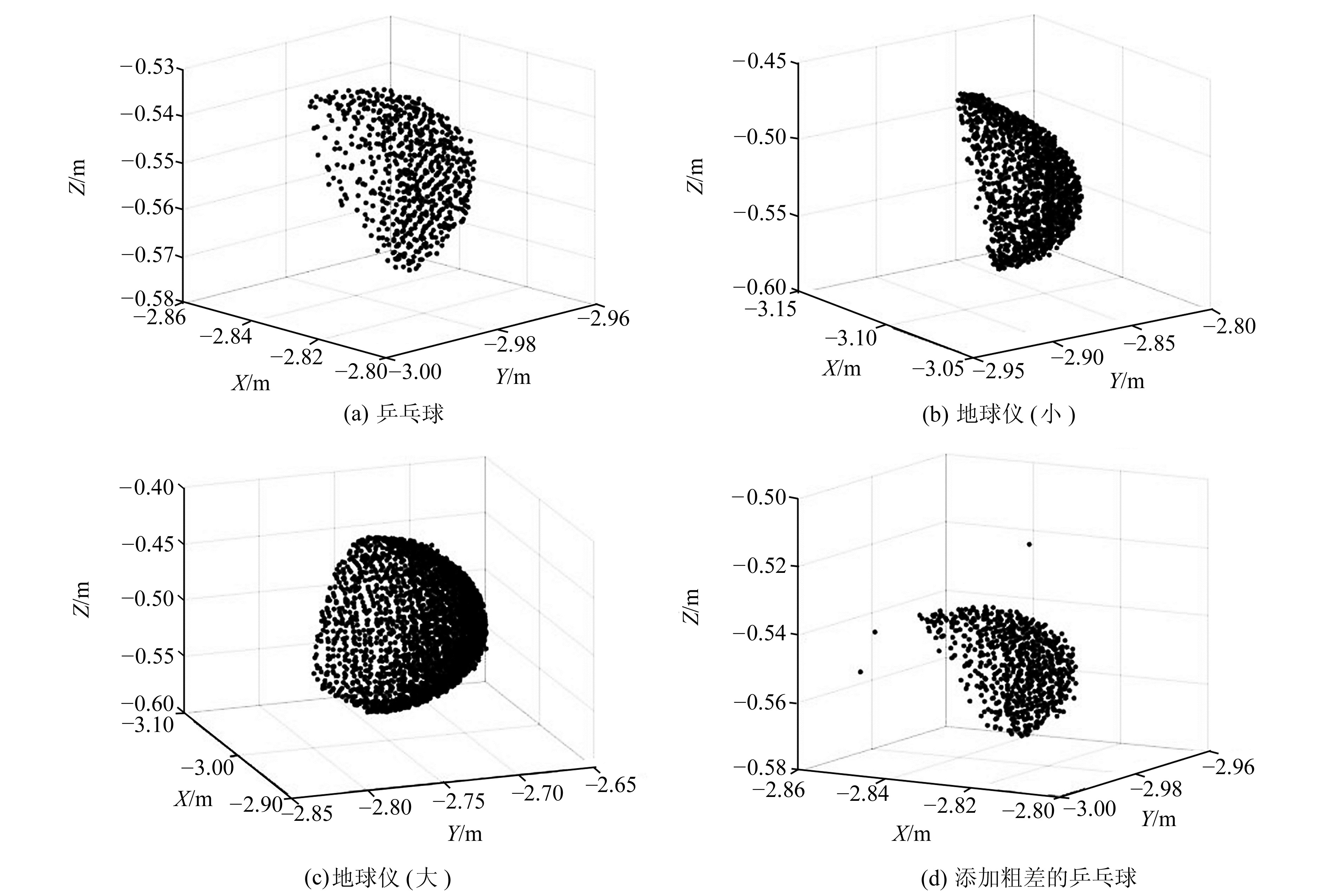
1) 设置扫描间隔为5 mm, 对半径19.8 mm的乒乓球、半径51.4 mm和71.7 mm的地球仪分别进行扫描,结果如图 2(a)、2(b)、2(c)。
|
图 2 4种标靶扫描点云 Fig. 2 Point cloud of four sphere targets |
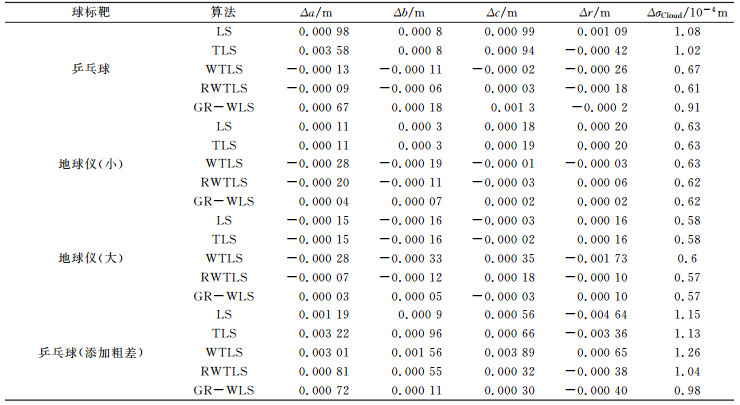
2) 采用Leica Cyclone软件计算。由于点云拟合精度很高,可以作为真值(表 1)。再利用LS、TLS、WTLS、RWTLS和GR-WLS 5种方法计算球标靶的球心坐标和半径,利用式(4)求得球面点云的拟合精度,与表 1中计算的真值作比较(表 2)。
|
|
表 1 Leica Cyclone软件计算结果 Tab. 1 Calculation results of Leica Cyclone |
|
|
表 2 5种方法计算结果 Tab. 2 Calculation results of five methods |
3) 在乒乓球扫描点云中人为地使10个扫描点成为异常点[11](图 2(d)),采用Leica Cyclone软件计算,见表 1。再利用LS、TLS、WTLS、RWTLS和GR-WLS 5种方法计算球标靶的球心坐标和半径,利用式(4)求得球面点云的拟合精度,与表 1中计算的真值作比较(表 2)。
1) 由两个地球仪标靶和添加粗差后的乒乓球标靶计算结果可见,GR-WLS的拟合精度最优,其计算得到的球心坐标与半径更接近于Cyclone软件计算结果。而在没有添加粗差的乒乓球计算结果中,GR-WLS次于WTLS和RWTLS。因为两个地球仪与支架的连接处有较大的卡口,在扫描时引入粗差,而没有添加粗差的乒乓球可以认为不含粗差点。GR-WLS方法能有效地利用截面圆约束剔除较多的粗差点,具有更好的抗粗差能力。对于不含粗差的点云,其处理效果弱于WTLS和RWTLS。
2) 从有粗差的地球仪和乒乓球计算结果可以看出,WTLS方法的拟合精度、圆心坐标和半径与真值相差较大,粗差对WTLS影响较大,其原因是以先验信息确定的协因数阵与实际的协因数阵有偏差,导致解算的可信度降低。
3) 在4种标靶扫描数据的计算结果中,TLS和LS的计算结果都较差,因为TLS和LS没有考虑入射角角度对点位精度的影响。
3 结语实验结果表明,本文方法具有一定的准确性、稳健性和抗粗差能力,在球标靶的特征提取应用中具有重要的意义;从几何关系的角度分析,更能直观清晰地了解球标靶特征提取的原理。
| [1] |
Shakarji C M. Least-Squares Fitting Algorithms of the NIST Algorithm Testing System[J]. Journal of Research of the National Institute of Standards and Technology, 1998, 103(6): 633-641 DOI:10.6028/jres
(  0) 0) |
| [2] |
鲁铁定, 周世健, 张立亭, 等. 基于整体最小二乘的地面激光扫描标靶球定位方法[J]. 大地测量与地球动力学, 2009, 29(4): 102-105 (Lu Tieding, Zhou Shijian, Zhang Liting, et al. Sphere Target Fixing of Point Cloud Data Based on TLS[J]. Journal of Geodesy and Geodynamics, 2009, 29(4): 102-105)
(  0) 0) |
| [3] |
陈玮娴, 陈义, 袁庆, 等. 加权总体最小二乘在三维激光标靶拟合中的应用[J]. 大地测量与地球动力学, 2010, 30(5): 90-96 (Chen Weixian, Chen Yi, Yuan Qing, et al. Application of Weighted Total Least Squares to Target Fitting of Three-Dimensional Laser Scanning[J]. Journal of Geodesy and Geodynamics, 2010, 30(5): 90-96)
(  0) 0) |
| [4] |
官云兰, 詹新武, 程效军, 等. 一种稳健的地面激光扫描标靶球定位方法[J]. 工程勘察, 2008(10): 42-45 (Guan Yunlan, Zhan Xinwu, Cheng Xiaojun, et al. Spherical Target Positioning of 3D Laser Scanning Based on a Robust Method[J]. Geotechnical Investigation Surveying, 2008(10): 42-45)
(  0) 0) |
| [5] |
王乐洋, 陈汉清, 林永达, 等. 利用稳健WTLS方法进行三维激光扫描标靶球定位[J]. 大地测量与地球动力学, 2016, 36(8): 746-749 (Wang Leyang, Chen Hanqing, Lin Yongda, et al. Spherical Target Positioning of 3D Laser Scanning by Using Robust WTLS Method[J]. Journal of Geodesy and Geodynamics, 2016, 36(8): 746-749)
(  0) 0) |
| [6] |
黄莉. 空间过点与直线的平面方程的求法[J]. 职大学报, 2014(6): 73-74 (Huang Li. Method for Finding the Equation of the Plane with a Point and a Straight Line[J]. Journal of the Staff and Worker's University, 2014(6): 73-74 DOI:10.3969/j.issn.1671-1440.2014.06.019)
(  0) 0) |
| [7] |
闫振仁. 直线与圆的方程[J]. 中学数学教学参考, 2016(1): 109-111 (Yan Zhenren. Linear and Circular Equations[J]. Teaching Reference of Middle School Mathematics, 2016(1): 109-111)
(  0) 0) |
| [8] |
苍桂华, 李明峰, 岳建平. 以入射角定权的点云数据加权总体最小二乘平面拟合研究[J]. 大地测量与地球动力学, 2014, 34(3): 95-99 (Cang Guihua, Li Mingfeng, Yue Jianping. Study on Point Clouds Plane Fitting with Weighted Total Least Squares Based on Incidence Angle Weighting[J]. Journal of Geodesy and Geodynamics, 2014, 34(3): 95-99)
(  0) 0) |
| [9] |
Soudarissanane S, Lindenbergh R, Menmenti M, et al. Scanning Geometry: Influencing Factor on the Quality of Terrestrial Laser Scanning Points[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2011, 66(4): 389-399 DOI:10.1016/j.isprsjprs.2011.01.005
(  0) 0) |
| [10] |
张永春, 达飞鹏, 宋文忠. 三维散乱点集的曲面三角剖分[J]. 中国图像图形学报, 2003, 8(12): 1 379-1 388 (Zhang Yongchun, Da Feipeng, Song Wenzhong. Surface Triangulations Based on 3D Arbitrary Point-Sets[J]. Journal of Image and Graphics, 2003, 8(12): 1 379-1 388)
(  0) 0) |
| [11] |
官云兰, 刘绍堂, 周世健, 等. 基于整体最小二乘的稳健点云数据平面拟合[J]. 大地测量与地球动力学, 2011, 31(5): 80-83 (Guan Yunlan, Liu Shaotang, Zhou Shijian, et al. Robust Plane Fitting of Point Clouds Based on TLS[J]. Journal of Geodesy and Geodynamics, 2011, 31(5): 80-83)
(  0) 0) |
2. School of Civil Engineering, Chongqing University, 174 Shazheng Street, Chongqing 400044, China
 2017, Vol. 37
2017, Vol. 37