2. 流域生态与地理环境监测国家测绘地理信息局重点实验室,南昌市广兰大道418号,330013;
3. 江西省数字国土重点实验室,南昌市广兰大道418号,330013
系统误差与粗差和偶然误差一样,一直是测量平差所研究的问题之一,如何减弱和消除系统误差的影响是提高成果精度的重要内容。在实际应用中,需要对系统误差进行补偿、量化甚至消除,或者对观测值进行加减常数、乘以系数等方法进行处理,从而使观测值中仅含有偶然误差[1]。随着大地测量的发展逐步面向太空,对测量精度的要求不断提高,对平差结果的精度要求也越来越高,而常规方法并不能满足。关于如何处理系统误差,周江文[2]从“部分延续”模式出发,对系统误差取用了相应的权阵,将问题转化为常规处理;陶本藻等[3-4]把系统误差纳入平差模型的模型误差中,把系统误差当作参数求解,从整体上减弱和消除其影响,保证参数本应具有的精度,并通过假设检验来验证附加系统参数模型是否正确及附加系统参数的引入是否合理;文献[5]研究了系统误差对参数估值的影响。考虑到仪器、观测环境等原因,观测数据不可避免地含有误差,由观测值组成的系数矩阵亦带有随机误差,因此仅考虑到观测向量含有随机误差的附加系统参数的平差方法的解算结果并非是最优解。
本文从传统的附加系统参数模型[6]出发,针对该平差模型进行重构,研究尺度比参数的附加系统参数的Partial EIV模型,通过两个算例对本文方法与传统方法进行分析和比较。
1 水准测量中尺度比参数的附加系统参数的Partial EIV模型Partial EIV模型为[7]:
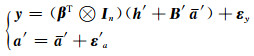
|
(1) |
随机模型为:
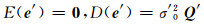
|
(2) |
式中,⊗为Kronecker积,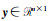
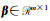
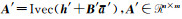
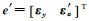
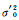
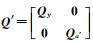
相应地,水准测量中尺度比参数的附加系统参数的Partial EIV模型为:
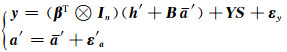
|
(3) |
式中,Y为由观测高差组成的n×u系数矩阵,S为u×1附加系统参数,即尺度比参数。
在水准测量中,A′是固定的常数矩阵,而系数矩阵Y与观测值有关,故令A= [A′ Y],X = [β S]T。对式(3)进行变形,转化为附加系统参数的Partial EIV模型:
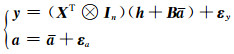
|
(4) |
随机模型为:
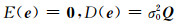
|
(5) |
式中,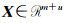
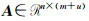
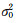
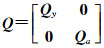
将式(4)变形转化为[8]:
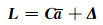
|
(6) |
式中,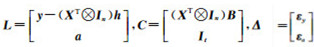
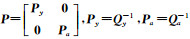
令Δ的估值为V,a的估值为â,则式(6)的误差方程为:
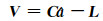
|
(7) |
通过文献[8]的公式推导得:
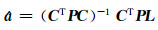
|
(8) |
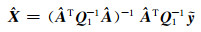
|
(9) |
式中,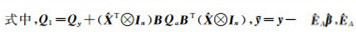
验后单位权中误差公式及模型参数的近似精度评定公式为[8]:

|
(10) |
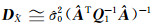
|
(11) |
算法的迭代流程如下。
1) 初值: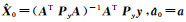
2) 由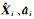
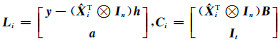
3) 将步骤2)求得的Li、Ci代入公式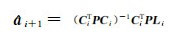
4) 将âi+1重构改正后的系数矩阵Âi+1, 得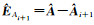
5) 计算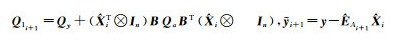
6)由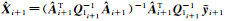
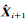
7) 重复步骤2)~6),直至满足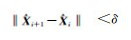
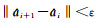
由于加入的附加系统参数改变了原有的模型,这导致了引入该参数是否合理的问题。若需引入但不加以选择,可能导致参数过多,从而造成法方程病态。为避免此类问题,应对附加系统参数模型和参数的正确性进行检验[9]。
2.1 模型合理性检验平差定权时的先验单位权方差为σ02,引入附加参数后求得方差估计值为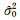
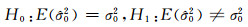
|
(12) |
采用χ2检验法,构造统计量:
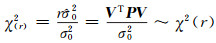
|
(13) |
对于给定置信水平α,自由度为r,查χ2分布表,若统计量满足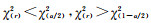
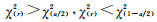
采用t检验法,检验的原假设H0和备选假设H1分别为:
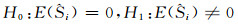
|
(14) |
构造t分布统计量:
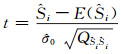
|
(15) |
在H0成立下,则有t统计量:
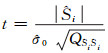
|
(16) |
在显著水平α下,若统计量t>tα/2,则拒绝H0,接受H1,表明引入附加系统参数Ŝi是必要的,即Ŝi是显著的附加系统参数。
3 算例与分析在算例中,运用本文的方法(方法1)和文献[6]中的方法,即基于最小二乘的附加系统参数平差方法(方法2)分别进行计算。
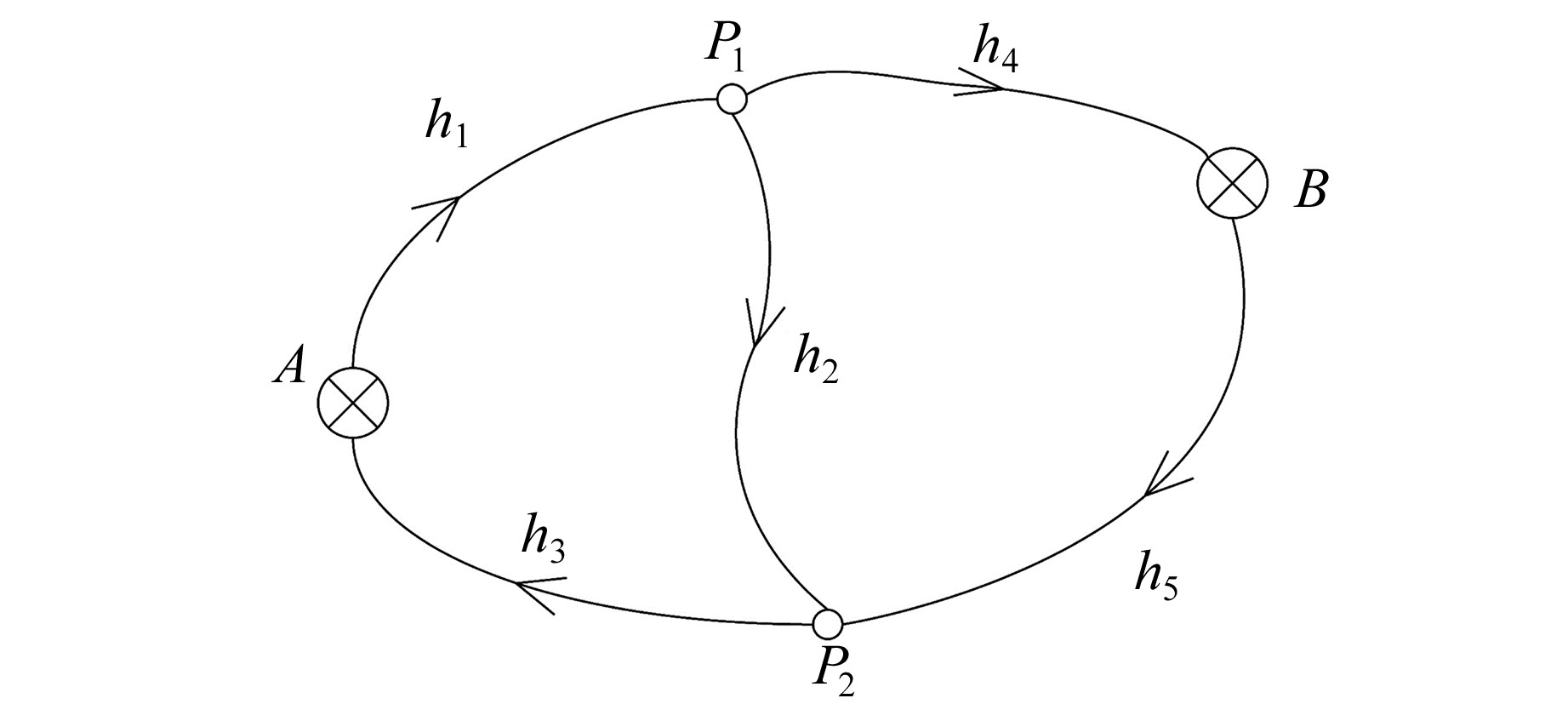
3.1 算例1该算例来自于文献[9]。如图 1所示,A、B为已知水准点,HA=1.000 m,HB=10.000 m,观测高差h1=3.586 m,h2=0.529 m,h3=-4.110 m,h4=5.422 m,h5=-4.901 m,求高程平差值及可能存在的尺度改正Ŝ。
|
图 1 水准网示意图 Fig. 1 Schematic diagram of leveling network |
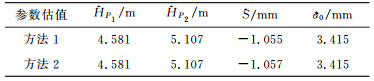
两种方法求得的参数估值如表 1所示,由方法1计算得到的系数矩阵残差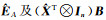
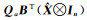
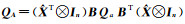
|
|
表 1 不同方法得到的参数估值 Tab. 1 The estimated parameters obtained by different methods |

|
(17) |
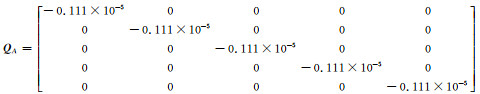
|
(18) |
由式(16)构造t分布统计量:
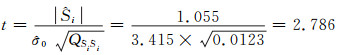
|
选定显著水平α=0.05,以自由度为2查t分布表得t0.0025=4.31,因t=2.786<4.31,故接受原假设H0,拒绝备选假设H1,表明引入的附加系统参数不显著。
3.2 算例2模拟水准测量网如图 1所示,A、B为已知水准点,P1、P2为待测点,各高差观测值真值及路线长度如下:h1=0.296 m,S1=1 km;h2=-0.099 m,S2=2 km;h3=-0.197 m,S3=2 km;h4=0.197 m,S4=2 km;h5=-0.296 m,S5=1 km。模拟真值HP1=10.300 m,HP2=10.200 m。设先验单位权方差
|
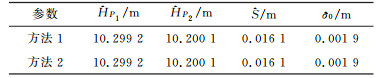
|
表 2 不同方法得到的参数估值 Tab. 2 The estimated parameters obtained by different methods |
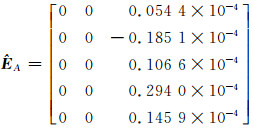
|
(19) |
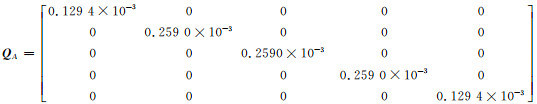
|
(20) |
由式(13)构造统计量:
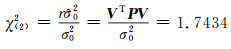
|
选定显著水平α=0.05,以自由度为2查χ2分布表得χ(0.025)2=7.378, χ(0.975)2=0.051,因χ(2)2=1.7434满足接受原假设H0的条件,表明引入的附加参数总体合理。
由式(16)构造t分布统计量:
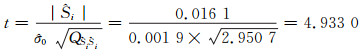
|
选定显著水平α=0.05,以自由度为2查t分布表得t0.0025=4.31,因为t=4.933 0>4.31,故拒绝原假设H0,接受H1,认为引入的附加系统参数显著。
3.3 分析从实际算例和模拟算例看出,本文方法与传统方法计算得到的参数结果基本一致,即水准测量中尺度比参数的附加系统参数的Partial EIV模型,与传统的附加系统参数的平差法效果基本一致。
从式(17)和(19)看出,系数矩阵残差的值是一个接近零的数,可以忽略不计[10]。本文中,水准测量精确到mm级的单位即可满足精度要求,但系数矩阵残差数值的单位已经超过mm级,说明系数矩阵残差对系数矩阵的影响可忽略不计,这是基于Partial EIV模型的水准测量中尺度比参数的附加系统参数的方法对系数矩阵残差改正效果并不明显的原因。此外,利用顾及系数矩阵误差的总体最小二乘方法得到的计算结果与传统的最小二乘方法基本一致[11-13],两者的区别在于系数矩阵是否含有随机误差。本文的两个算例中,ÊA≈ 0及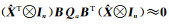
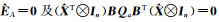
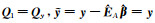
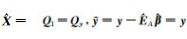
本文给出了水准测量中尺度比参数的附加系统参数的Partial EIV模型,相比于传统的基于最小二乘的附加系统参数的平差方法,本文方法更为严密。两种方法计算的参数结果对比分析可知,当系数矩阵的残差约等于零(即ÊA≈ 0)时,本文方法就退化为传统方法。
| [1] |
胡圣武, 肖本林. 现代测量数据处理理论与应用[M]. 北京: 测绘出版社, 2016 (Hu Shengwu, Xiao Benlin. Modern Theory and Application of Surveying Data Processing[M]. Beijing: Surveying and Mapping Press, 2016)
(  0) 0) |
| [2] |
周江文. 系统误差的数学处理[J]. 测绘工程, 1999, 8(2): 1-4 (Zhou Jiangwen. Mathematical Processing of Problems with Systematic Errors[J]. Engineering of Surveying and Mapping, 1999, 8(2): 1-4 DOI:10.3969/j.issn.1006-7949.1999.02.001)
(  0) 0) |
| [3] |
陶本藻, 施闯, 姚宜斌. 顾及系统误差的平差模型研究[J]. 测绘学院学报, 2002, 19(2): 79-81 (Tao Benzao, Shi Chuang, Yao Yibin. Research on Adjustment Model with Systematical Error[J]. Journal of Institute of Surveying and Mapping, 2002, 19(2): 79-81 DOI:10.3969/j.issn.1673-6338.2002.02.001)
(  0) 0) |
| [4] |
陶本藻. 系统误差的后验检验和平差补偿[J]. 大地测量与地球动力学, 2002, 22(1): 11-15 (Tao Benzao. Posterior Testing and Adjustment Compensation of Systematic Error[J]. Journal of Geodesy and Geodynamics, 2002, 22(1): 11-15)
(  0) 0) |
| [5] |
胡圣武, 吴军超, 冯弟飞. 系统误差对参数估值影响的研究[J]. 河南理工大学学报:自然科学版, 2016, 35(1): 55-58 (Hu Shengwu, Wu Junchao, Feng Difei. Research on Parameter Estimation Influence about System Error[J]. Journal of Henan Polytechnic University: Natural Science, 2016, 35(1): 55-58)
(  0) 0) |
| [6] |
沈云中, 陶本藻. 实用测量数据处理方法[M]. 北京: 测绘出版社, 2012 (Shen Yunzhong, Tao Benzao. Practical Methods for Surveying Data Processing[M]. Beijing: Surveying and Mapping Press, 2012)
(  0) 0) |
| [7] |
Xu P L, Liu J N, Shi C. Total Least Squares Adjustment in Partial Errors-In-Variables Models: Algorithm and Statistical Analysis[J]. Journal of Geodesy, 2012, 86(8): 661-675 DOI:10.1007/s00190-012-0552-9
(  0) 0) |
| [8] |
王乐洋, 余航, 陈晓勇. Partial EIV模型的解法[J]. 测绘学报, 2016, 45(1): 22-29 (Wang Leyang, Yu Hang, Chen Xiaoyong. An Algorithm for Partial EIV Model[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(1): 22-29)
(  0) 0) |
| [9] |
武汉大学测绘学院测量平差学科组. 误差理论与测量平差基础[M]. 武汉: 武汉大学出版社, 2009 (Surveying Adjustment Group of School of Geodesy and Geomatics, Wuhan University. Error Theory and Foundation of Surveying Adjustment[M]. Wuhan: Wuhan University Press, 2009)
(  0) 0) |
| [10] |
曾文宪. 系数矩阵误差对EIV模型平差结果的影响研究[D]. 武汉: 武汉大学, 2013 (Zeng Wenxian. Effect of the Random Design Matrix on Adjustment of an EIV Models and Its Reliability Theory[D]. Wuhan: Wuhan University, 2013)
(  0) 0) |
| [11] |
王乐洋, 陈汉清, 温扬茂. 地壳形变分析的总体最小二乘配置方法[J]. 大地测量与地球动力学, 2017, 37(2): 163-168 (Wang Leyang, Chen Hanqing, Wen Yangmao. Analysis of Crust Deformation Based on Total Least Squares Collocation[J]. Journal of Geodesy and Geodynamics, 2017, 37(2): 163-168)
(  0) 0) |
| [12] |
Schaffrin B, Felus Y A. On the Multivariate Total Least-Squares Approach to Empirical Coordinate Transformations[J]. Journal of Geodesy, 2008, 82(6): 373-383 DOI:10.1007/s00190-007-0186-5
(  0) 0) |
| [13] |
Xu P L, Liu J N, Zeng W X, 等. Effects of Errors-In-Variables on Weighted Least Squares Estimation[J]. Journal of Geodesy, 2014, 88(7): 705-716 (  0) 0) |
2. Key Laboratory of Watershed Ecology and Geographical Environment Monitoring, NASMG, 418 Guanglan Road, Nanchang 330013, China;
3. Jiangxi Province Key Lab for Digital Land, 418 Guanglan Road, Nanchang 330013, China
 2017, Vol. 37
2017, Vol. 37