2. 西安测绘研究所,西安市雁塔路中段1号,710054;
3. 中国科学院上海天文台,上海市南丹路80号,200030
目前,国外比较有名的电离层分析中心有CODE、ESOC、JPL、TUC,国内有CAS。各分析中心都采用自己的方法独立解算各自的最终(final)和快速(rapid)两种全球GIM产品,部分中心也有预报的GIM产品。此外, IGS和iGMAS也分别给出了国外、国内的综合电离层格网产品[1-2]。
文献[3]就4种最终电离层格网在中国区域的精度进行深入讨论,文献[4]就5种电离层格网在中国中纬和低纬地区的精度进行分析。然而, 目前就不同类型的GIM在全球范围的精度分析工作还没有展开。本文利用全球部分IGS站的数据,评估7家机构的最终、快速和预报GIM在全球范围内的符合精度,并进行分析讨论。
1 处理策略本文主要从全球选取部分IGS观测数据作为基准来分析不同分析中心不同类型的格网产品的性能。具体处理流程:1)首先对观测站的观测数据进行数据预处理(包括周跳、粗差探测与相位平滑伪距),然后求取IPP处的STEC,再按照三角投影函数(single-layer model,SLM)进行转换,得到IPP处的VTEC。至此,精确提取了测站不同历元IPP处的VTEC信息,以此作为基准。2)由不同分析中心的不同类型的GIM,按照一定的插值方法,求取不同测站不同历元IPP处的VTEC信息。3)利用1)中得到的基准,按照1.3中的绝对和相对统计指标,对比分析不同分析中心不同类型GIM的精度(注:本文是基于单层电离层假设,提取测站IPP处的VTEC信息)。
1.1 测站VTEC首先基于Bernese软件中的RNXSMT模块进行测站数据的预处理,然后利用IONAPS软件提取测站不同历元IPP处的TEC信息,同时利用CODE分析中心的DCB产品进行DCB改正,再利用SLM投影函数得到IPP处的VTEC信息。至此,得到了基于测站实测数据获得的IPP处的VTEC信息。
利用RNXSMT模块进行周跳、粗差以及码平滑处理的基本思路如下:首先利用M-W线性组合进行周跳和粗差探测,如式(1);其次若存在周跳,则利用与几何无关的线性组合确定周跳,如式(2);最后利用无电离层组合来去除M-W组合检测出的粗差,如式(3)、(4)所示:
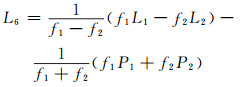
|
(1) |

|
(2) |

|
(3) |
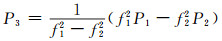
|
(4) |
式中,L6为M-W相位组合观测量;f1、f2为相应频点的频率;L1、L2为相应频点的载波相位观测值;P1、P2为相应频点的码观测值;L4为与几何无关的组合观测量;L3、P3分别为相位和码的无电离层组合观测量。
利用处理后的码和相位观测值来平滑伪距观测值,如式(5)、(6)所示。最后利用IONAPS软件,将平滑后的码观测值代入式(7),同时利用CODE中心的DCB产品,得到不同历元IPP处的VTEC。至此,基于测站数据的VTEC信息被精确提取。
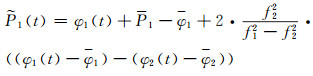
|
(5) |
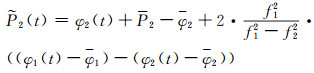
|
(6) |
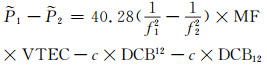
|
(7) |
式中,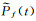
利用自编的SHICE模块,按照下面的插值方法,对不同类型GIM中VTEC进行插值,求出不同测站不同历元IPP处的VTEC。具体算法如下:首先按照时间线性内插,求得观测历元IPP处周围的4个格网点的VTEC值;然后按照空间线性内插,得到历元时刻IPP处的VTEC值:
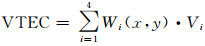
|
(8) |
式中,Wi(x, y)为权函数; Vi(i=1, 2, 3, 4)为4个格网点上的VTEC值。权函数的具体计算见参考文献[6]。
1.3 统计指标本文采用标准偏差(STD)和相对误差(ERROR)作为精度分析的指标, 其中STD是绝对指标,ERROR是相对指标,BIAS表示残差。其计算式为:
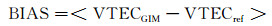
|
(9) |

|
(10) |
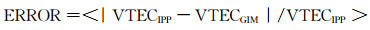
|
(11) |
式中,<>表示求和取平均;STD中<>里面的分母为N-1,N为观测历元数;VTECref为参考基准,本文将测站数据解算的IPP处的VTEC值作为参考基准。
2 算例本文在全球范围选取35个IGS站2016年1~100 d的数据作为分析各机构GIM内符合精度的基准,对CODE、ESA、UPC、JPL、CAS分析中心以及IGS和iGMAS服务中心的最终、快速和预报的GIM中的VTEC精度,按照高纬、中纬、低纬度进行分类统计;同时,对GIM中的卫星DCB信息也作统计分析(注:由于这些IGS站的观测数据参与了各中心的GIM解算,因此我们采用这些站作为基准,评估的GIM精度为内符合精度)。

|
图 1 所选测站及相应测站IPP的分布 Fig. 1 Distribution of stations and IPP of being selected |
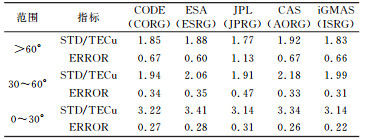
各机构的最终GIM、快速GIM以及预报GIM的统计情况见表 1~3。此外,为了反映不同GIM在观测时段内的变化特性,本文分别选取YELL、BJFS、ADIS 3个站作为高纬、中纬和低纬度带的代表,绘制了不同机构最终GIM的时间序列,见图 2~4。
|
|
表 1 各机构最终GIM产品的精度统计 Tab. 1 Accuracy statistics of final GIM products of different agencies |
|
|
表 2 部分机构快速GIM的精度统计 Tab. 2 Accuracy statistics of rapid GIM products of different agencies |
|
|
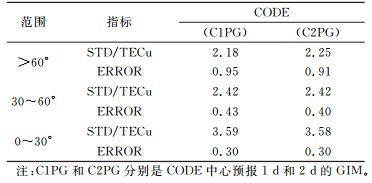
表 3 CODE预报GIM的精度统计 Tab. 3 Accuracy statistics of forecasting GIM products of CODE |
|
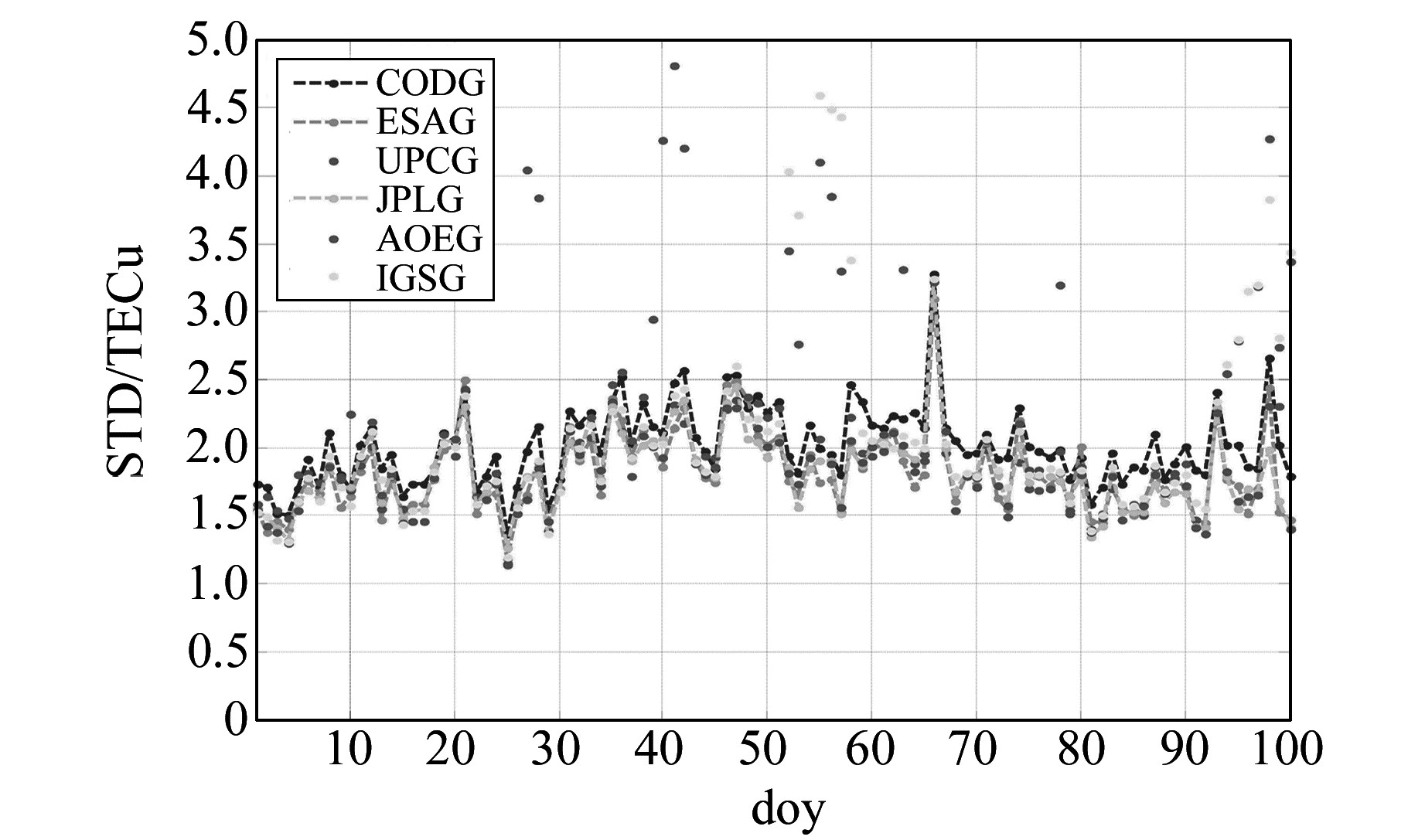
图 2 各机构2016年第1~100 d最终GIM在YELL站的STD Fig. 2 STD of final GIM products from doy 1 to 100 of 2016 at YELL of different agencies |
|
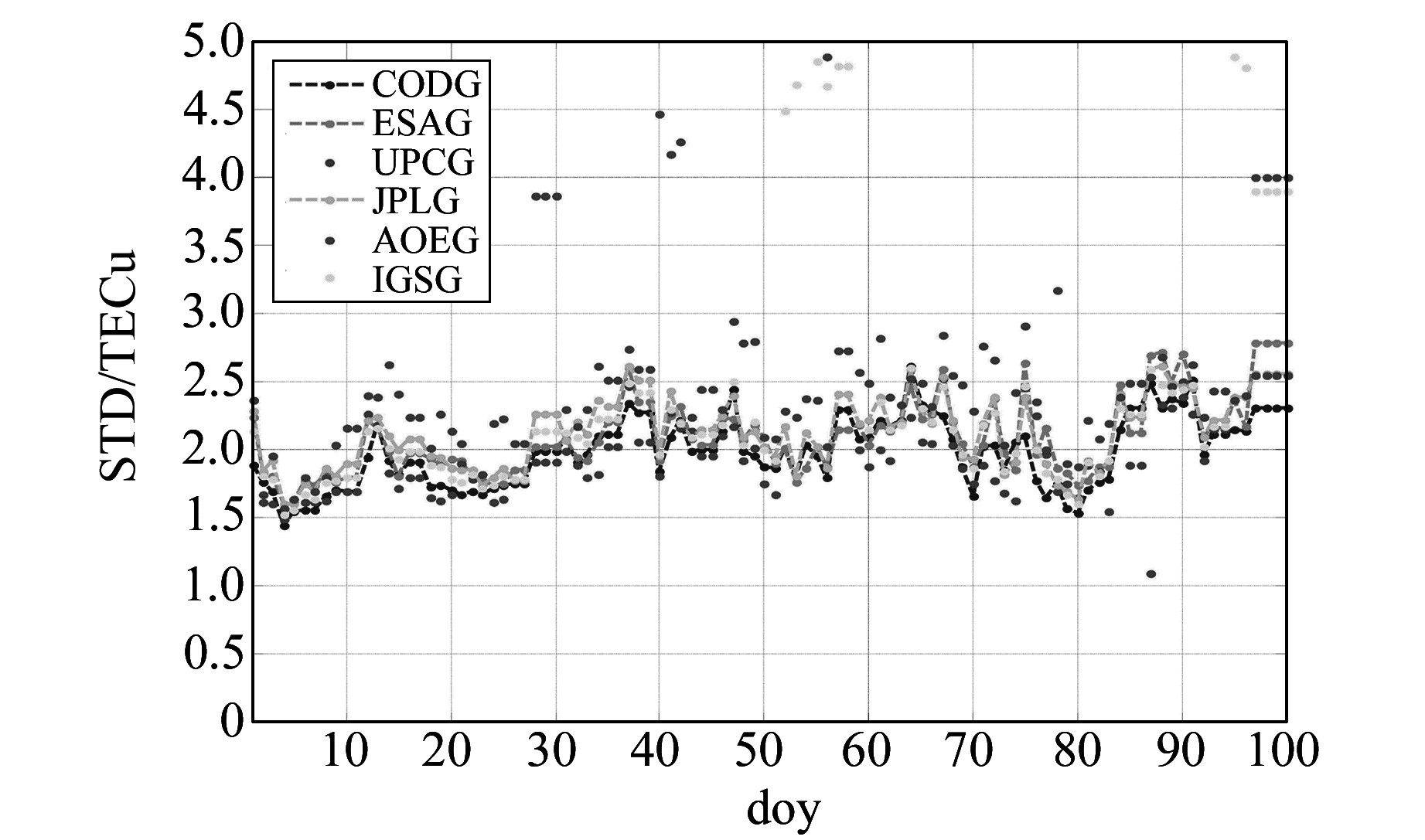
图 3 各机构2016年第1~100 d最终GIM在BJFS站的STD Fig. 3 STD of final GIM products from doy 1 to 100 in 2016 at BJFS of different agencies |
|
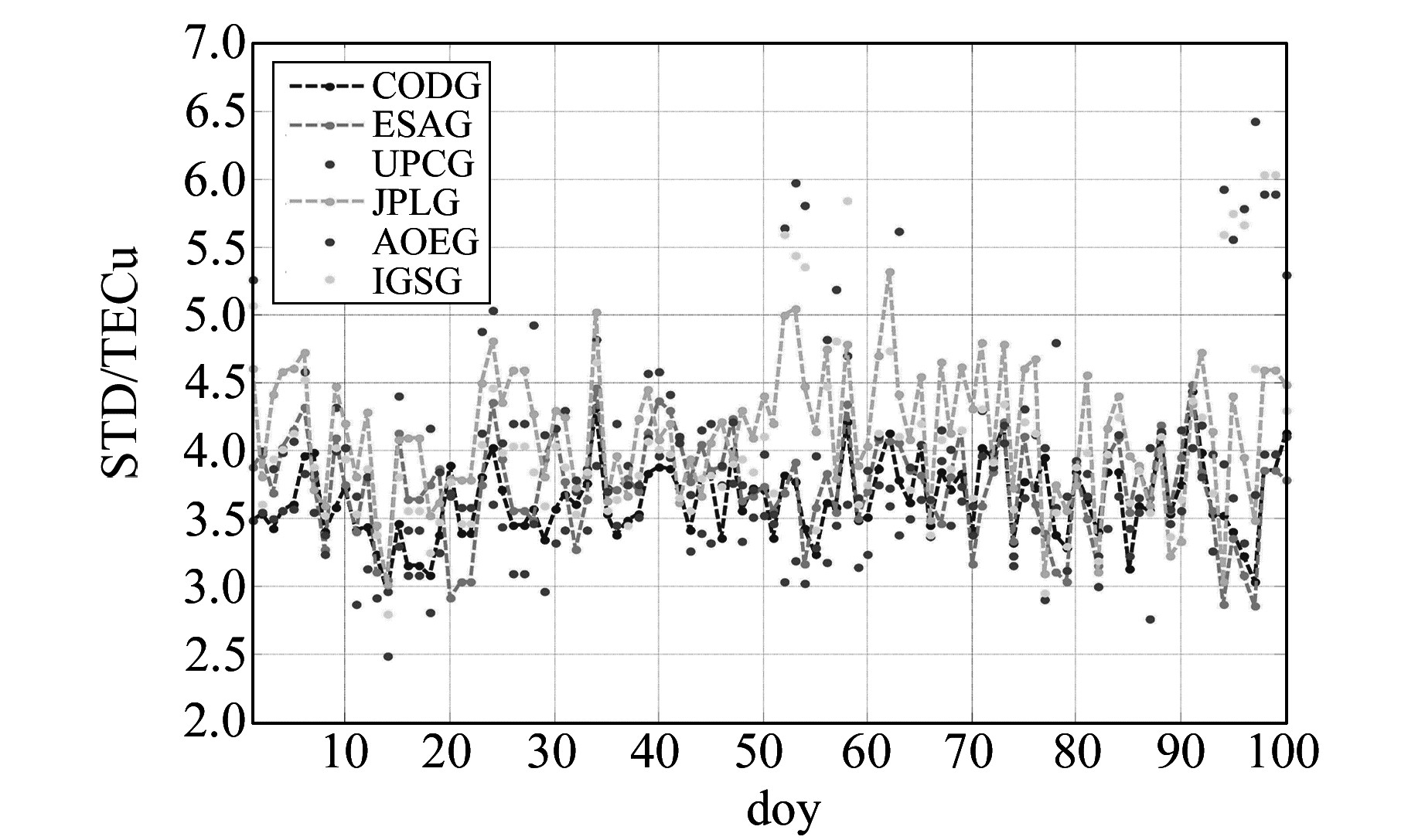
图 4 各机构2016年第1~100 d最终GIM在ADIS站的STD Fig. 4 STD of final GIM products from doy 1 to 100 of 2016 at ADIS of different agencies |
从式(10)和(11)可以看出,STD和ERROR越小,则格网精度越好。但是,文献[1]指出,ERROR可能存在与式(11)不一致的情况,因为在VTECIPP比较小的情况下,比如在夜晚或者电离层不活跃的区域,即使比较小的|VTECIPP-VTECGIM|,也会引起ERROR偏大。
从表 1以及图 2~4可以看出,各机构的最终GIM有以下特点:
1) 在表 2中,就STD而言,随着纬度的降低,各机构的最终GIM精度整体来看是依次降低的,从图 2~4中也可以得出类似结论。这与文献[3]给出的结论是一致的。
2) 就STD而言,无论是高纬、中纬还是低纬地区,CODE、ESA和JPL的GIM精度都比较好。在高纬地区,JPL的精度最好,其STD为1.76 TECu;各机构的STD最大偏差为0.25 TECu。在中纬地区,CODE的精度最好,其STD为1.78 TECu;各机构的STD最大偏差为0.45 TECu。在低纬地区,也是CODE的精度最好,其STD为2.84 TECu;各机构的STD最大偏差为0.58 TECu。
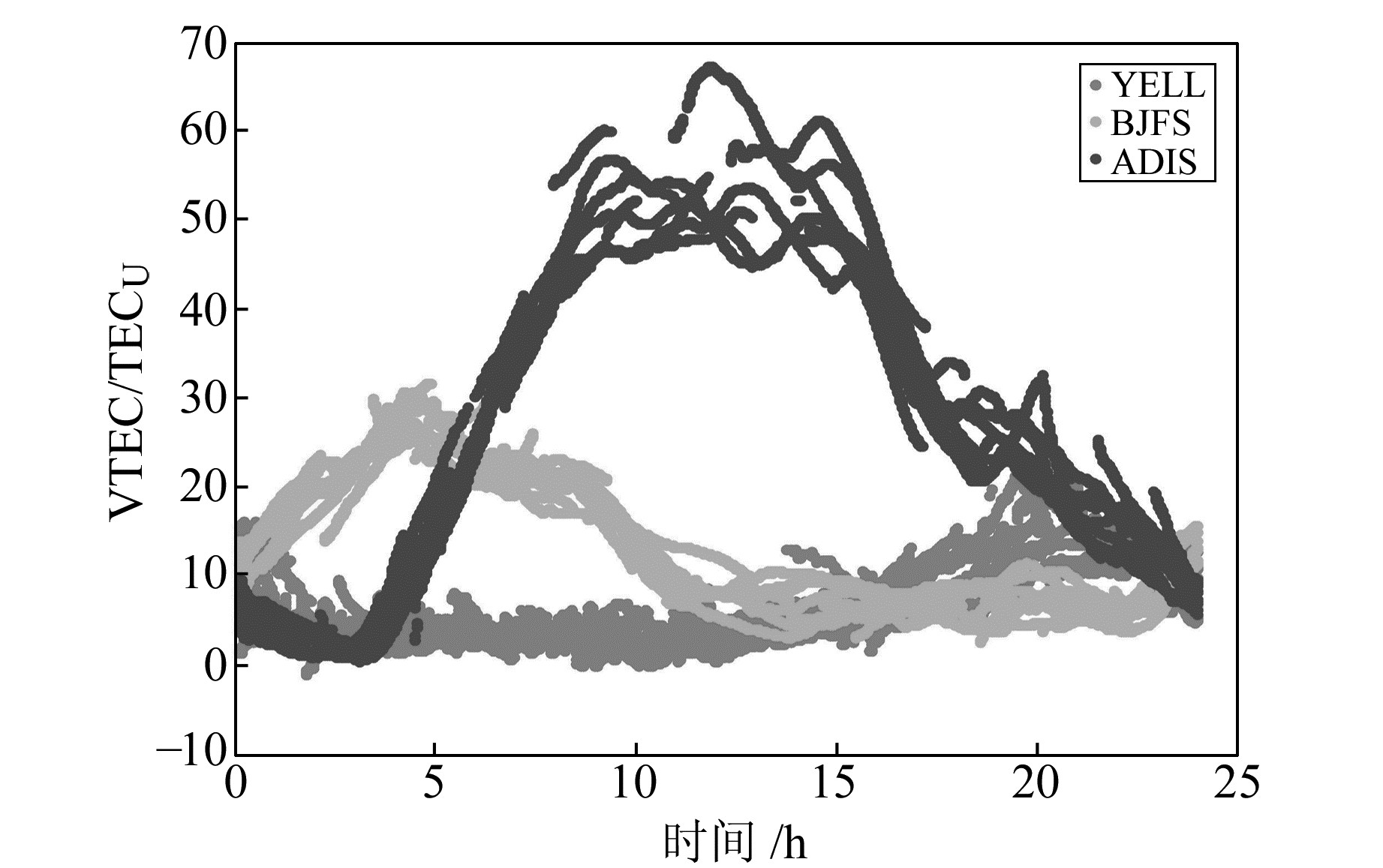
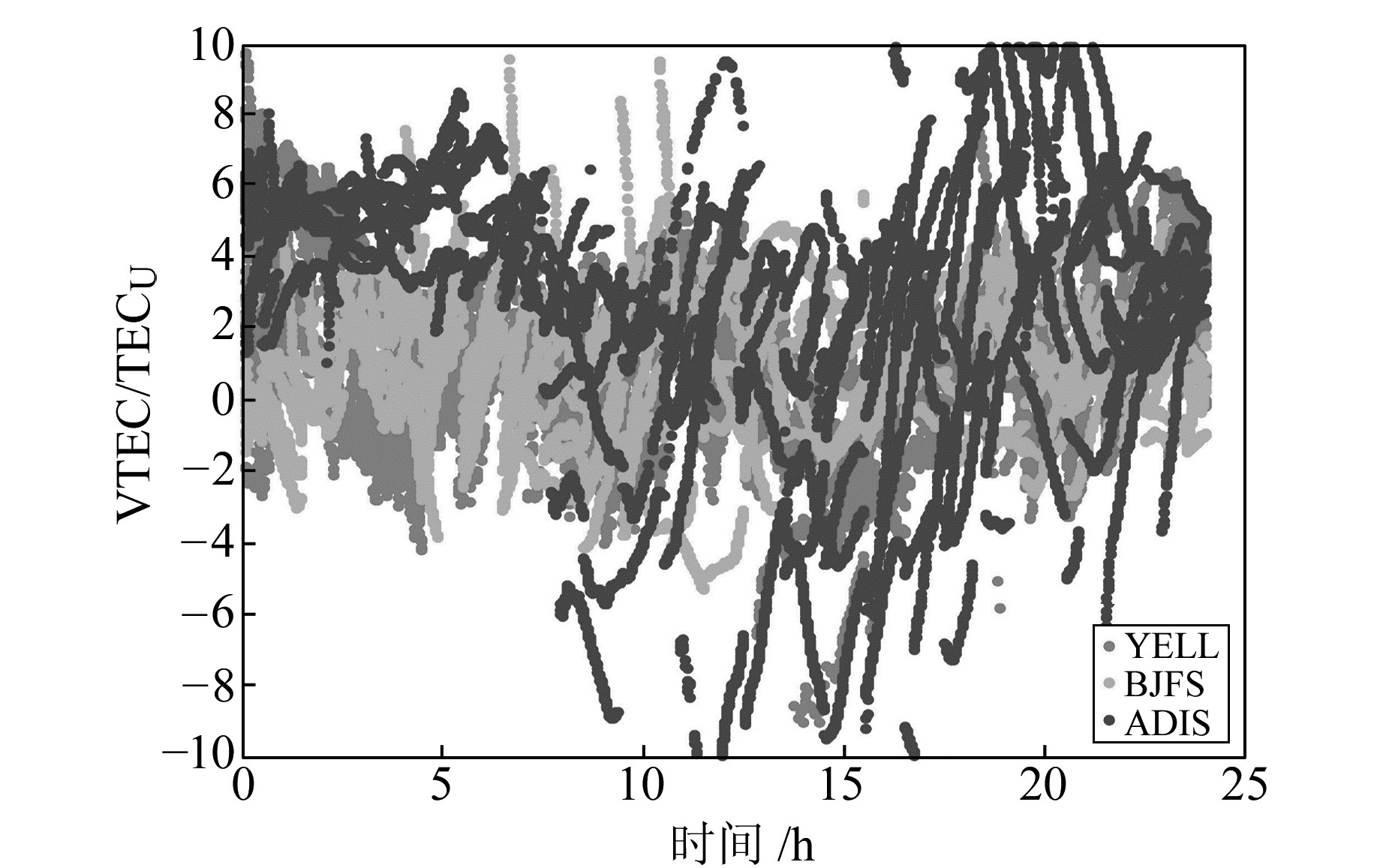
3) 就ERROR而言,在高纬、中纬和低纬地区,各机构的最大ERROR互差越来越小,分别为0.54、0.21和0.08。此外,随着纬度的降低,各机构的ERROR也越来越小。这两种现象并不能说明随着纬度的降低,各机构的GIM精度越来越好。图 6为在高、中、低纬度带3个测站的CODE的最终GIM与基准VTEC的偏差序列,即式(11)中的分子。图 5是各纬度带3个测站的基准VTEC序列,即式(11)中分母。可以看出,分母的增量远远大于分子的增量,这就可以解释前面提到的ERROR的两种情况。此外,图 5也反映出,随着纬度的降低,电离层越来越活跃。
|
图 5 2016年第50 d 3个高、中、低纬度测站的基准VTEC序列 Fig. 5 The VTEC series of datum of the three stations at different latitudes of doy 50 in 2016 |
|
图 6 2016年第50 d 3个高、中、低纬度测站的CODE最终GIM与基准VTEC的偏差序列 Fig. 6 The VTEC bias series of the three stations at different latitudes of doy 50 in 2016 |
4) 从图 2~4可以看出,就单测站而言,在YELL站,CAS、UPC和IGS的最终GIM在个别天数都有STD异常现象;在BJFS站,CAS和IGS也存在STD异常现象;在ADIS站,IGS和UPC存在STD异常现象。
从表 2可以看出,各机构快速GIM有如下特点:
1) 从STD看出,随着纬度的降低,各机构的快速GIM精度也依次降低。
2) 从STD看出,无论在高纬、中纬和低纬地区,CODE、JPL和iGMAS的快速GIM的精度都较好。在高纬地区,JPL的快速GIM精度最好,其STD为1.77 TECu,各机构的STD最大偏差为0.15 TECu;在中纬地区,JPL的快速GIM精度最好,其STD为1.91 TECu, 各机构的STD最大偏差为0.27 TECu;在低纬地区,JPL和iGMAS的精度最好,其STD均为3.14 TECu, 各机构的STD最大偏差为0.27 TECu。
|
|
表 4 CAS机构异常情况精度统计 Tab. 4 Accuracy statistics of abnormal situations for CAS |
从表 3可看出, CODE预报GIM有如下特点:
1) 从STD看出,随着纬度的降低,CODE的预报GIM精度降低。
2) 从STD看出,在高纬度地区,预报1 d的GIM要比预报2 d的GIM精度要好些;在中纬和低纬度地区,两种预报GIM的精度相当。
1) 从STD整体看来,各机构的最终GIM精度要高于快速GIM精度,预报GIM精度在3类产品中精度最差。
2) 从STD可看出,CAS机构的快速GIM比最终GIM精度要好。
2.2 卫星DCB统计分析各机构GIM中,除了包含格网VTEC信息外,还有另一种重要的信息——卫星DCB。统计了不同机构2016年第32~60 d最终和快速GIM中所有GPS和GLONASS卫星的平均DCB信息。考虑到CODE发布DCB产品是每颗卫星每月给出一个值,在这里我们也是每颗卫星每月给一个值。统计情况见图 7~10。
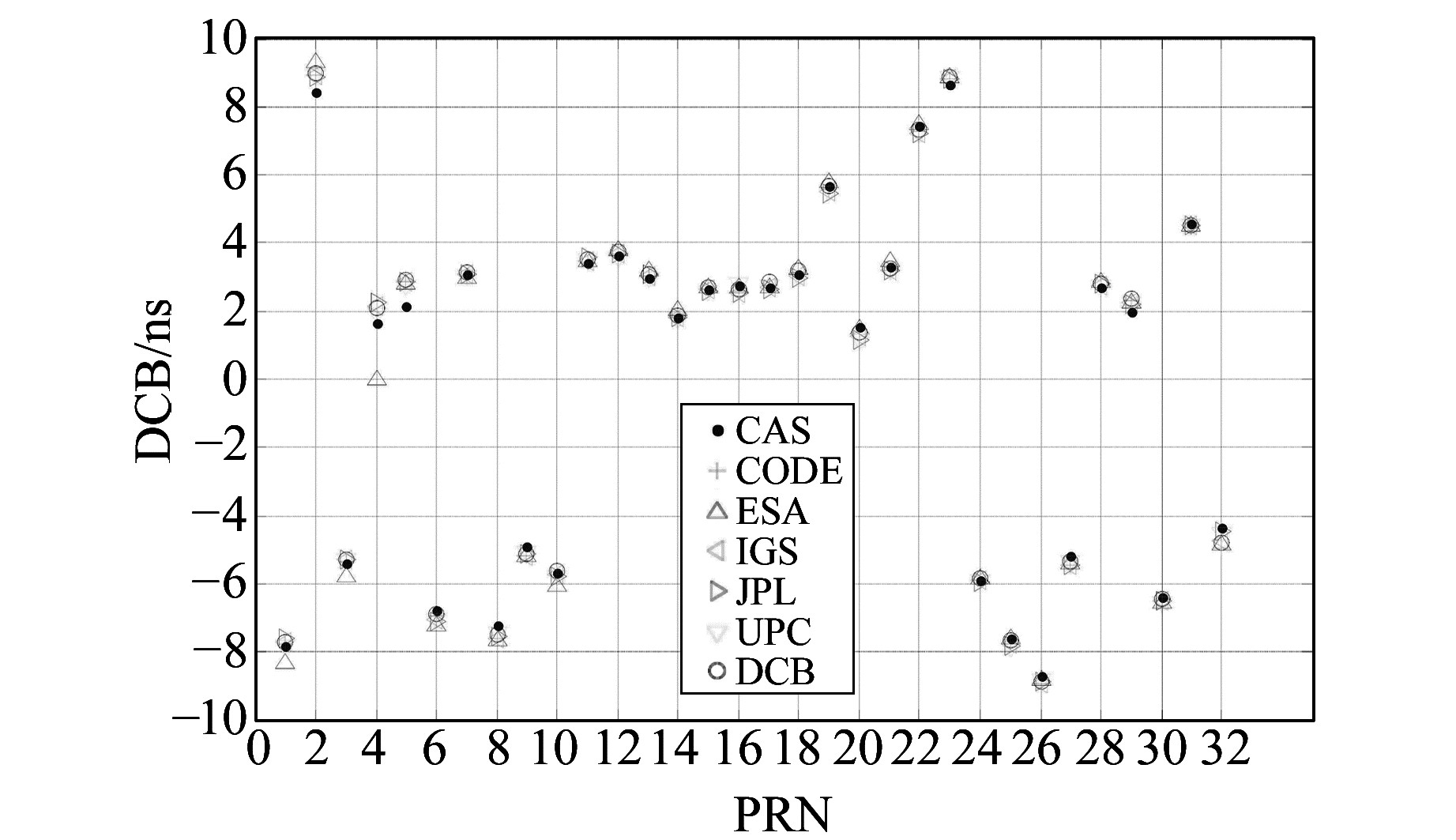
|
图 7 各机构最终GIM在2016年第32~60 d GPS卫星平均DCB Fig. 7 The average GPS satelites DCB of final GIM products from doy 32 to 60 in 2016 of different agencies |
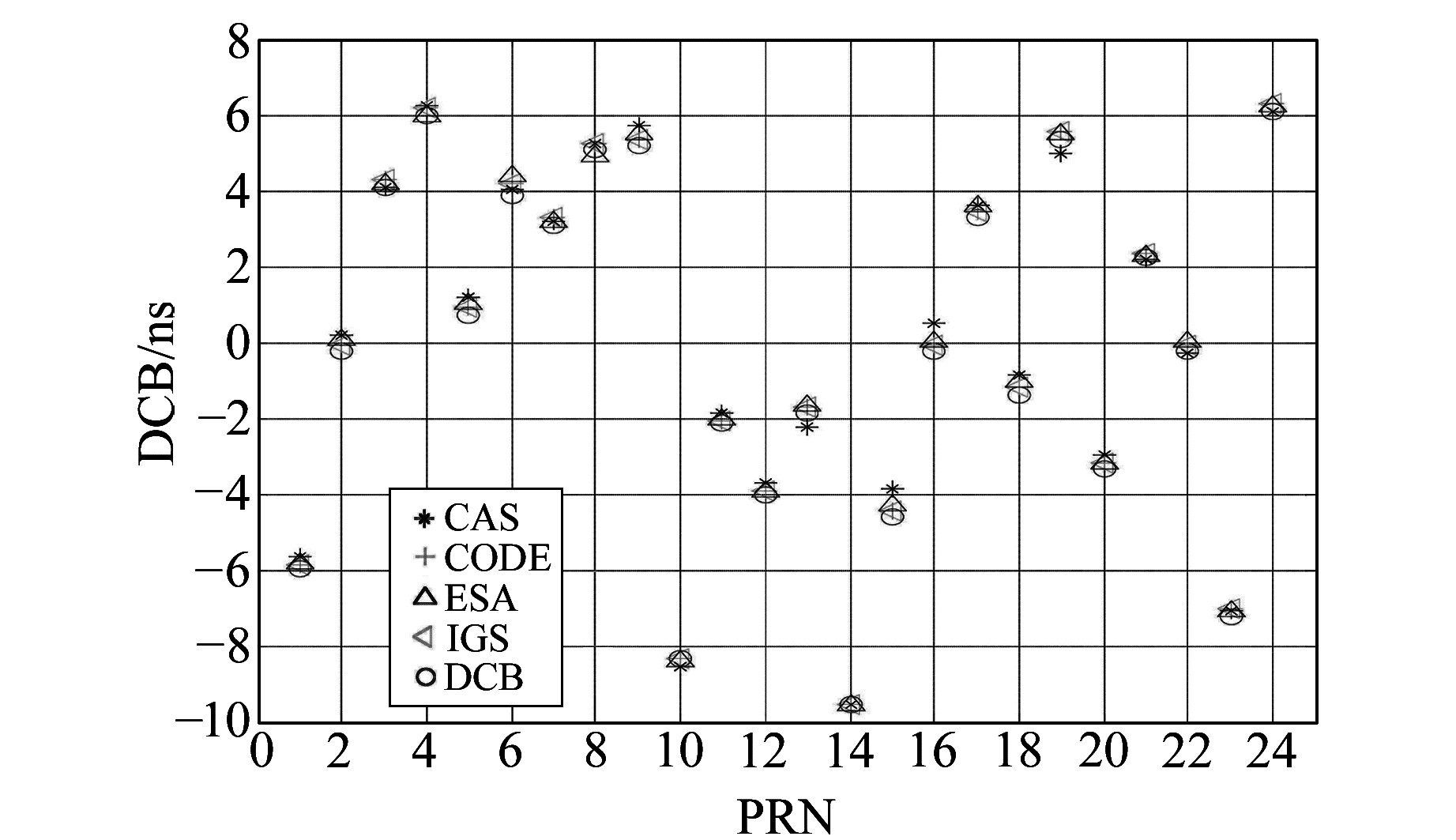
|
图 8 各机构最终GIM在2016年第32~60 d GLONASS卫星平均DCB Fig. 8 The average GLONASS satelites DCB of final GIM products from doy 32 to 60 in 2016 of different agencies |
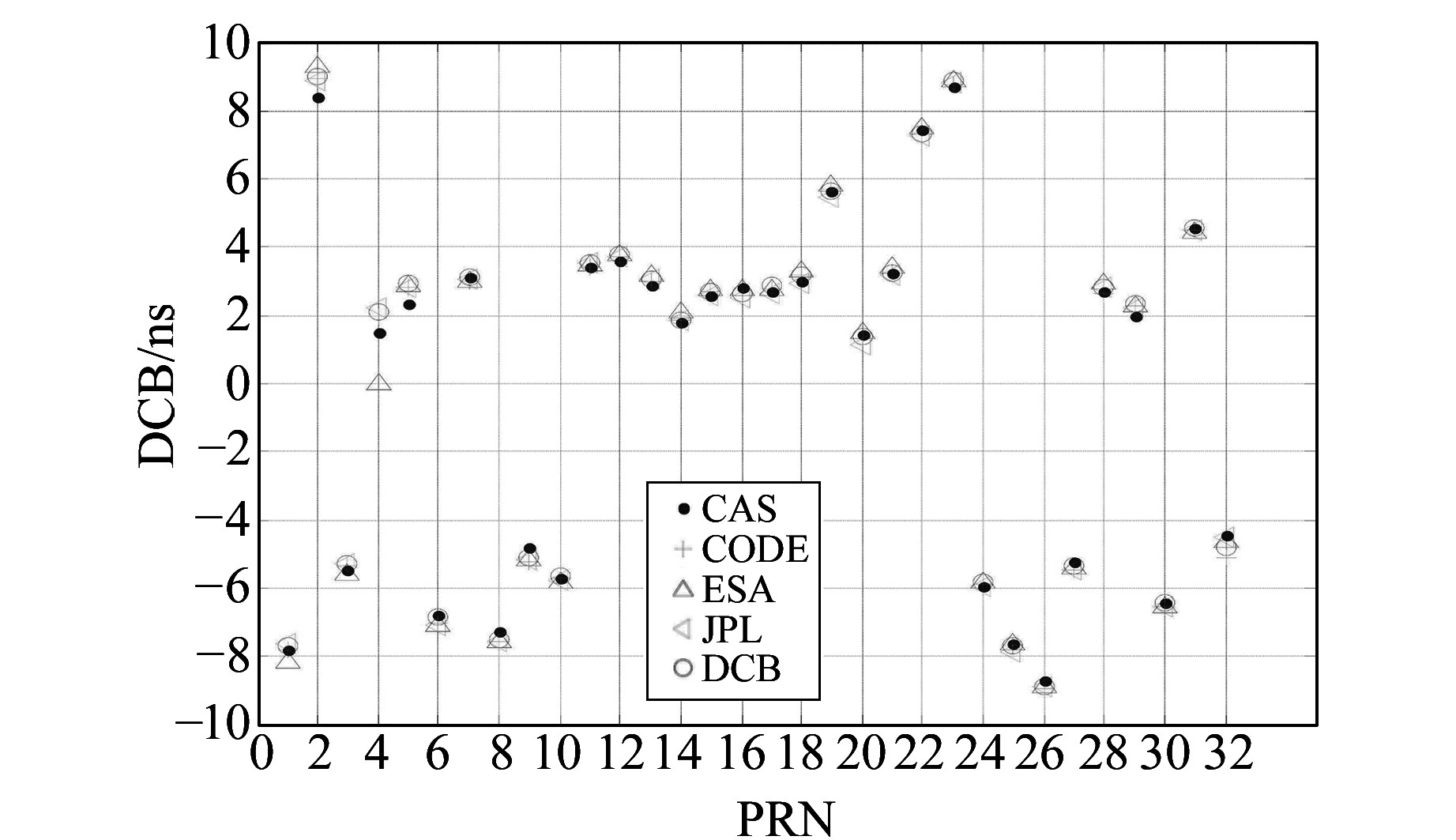
|
图 9 各机构快速GIM在2016年第32~60 d GPS卫星平均DCB Fig. 9 The average GPS satelites DCB of rapid GIM products from doy 32 to 60 in 2016 of different agencies |
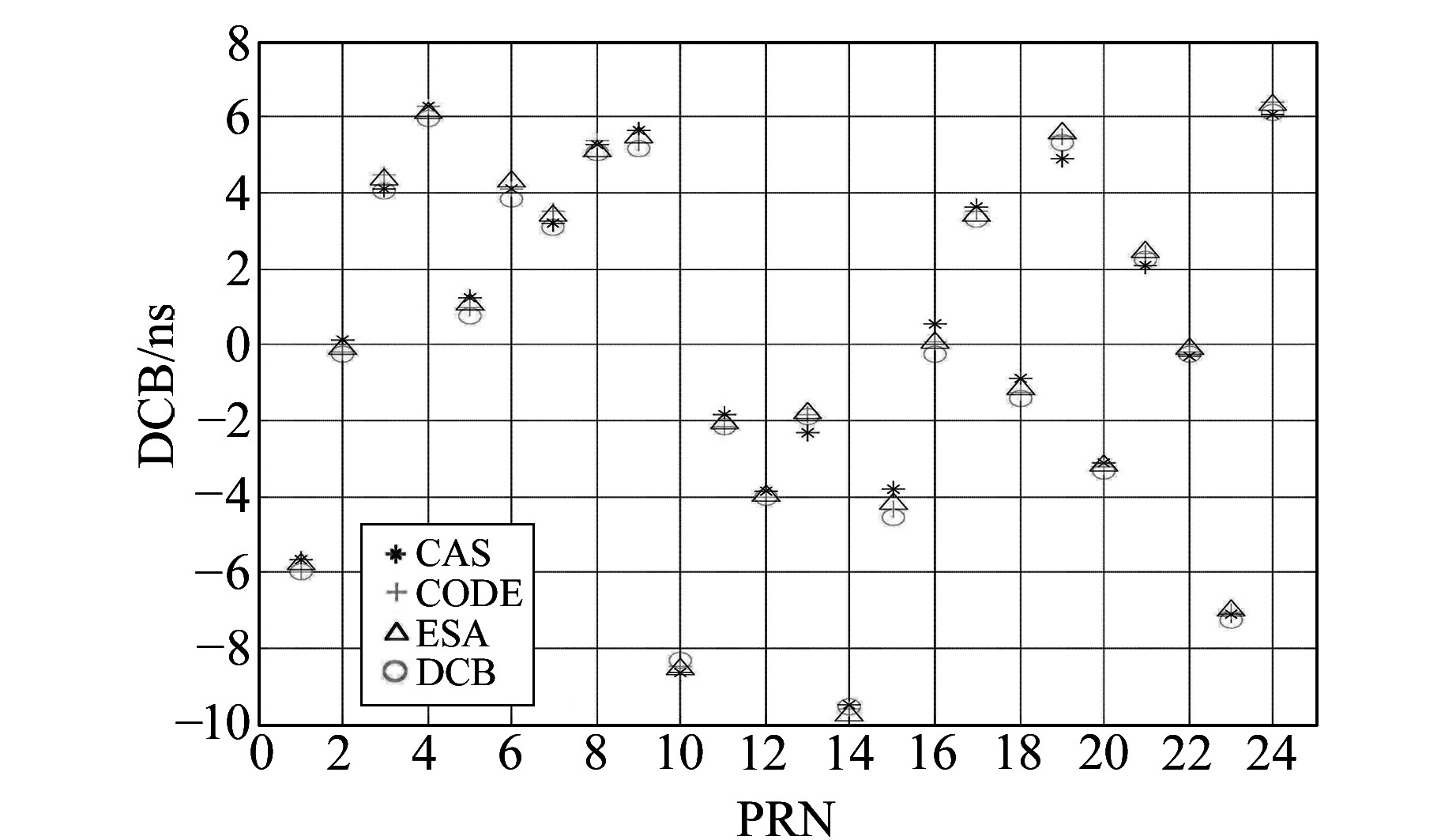
|
图 10 各机构快速GIM在2016年第32~60 d GLONASS卫星平均DCB Fig. 10 The average GLONASS satelites DCB of rapid GIM products from doy 32 to 60 in 2016 of different agencies |
1) 无论是最终GIM,还是快速GIM,各机构的大部分GPS卫星的一致性比较好,并且各机构的最终GIM和快速GIM之间的一致性也比较好。
2) CAS机构在最终和快速GIM中2、4、5号GPS卫星的DCB均与其他机构有一定差异;同样,ESA机构在最终和快速GIM中1、3、4号GPS卫星的DCB与其他机构也有一定差异,其中4号GPS卫星DCB为0,这是因为ESA在解算时,将4号GPS卫星剔除的缘故。
为进一步分析差异的原因,单独绘制CAS机构2、4、5号GPS卫星DCB在最终和快速GIM中的时间序列,如图 11、12所示,以及ESA机构1、3号GPS卫星DCB在最终和快速GIM中的时间序列,如图 13、14所示。
|
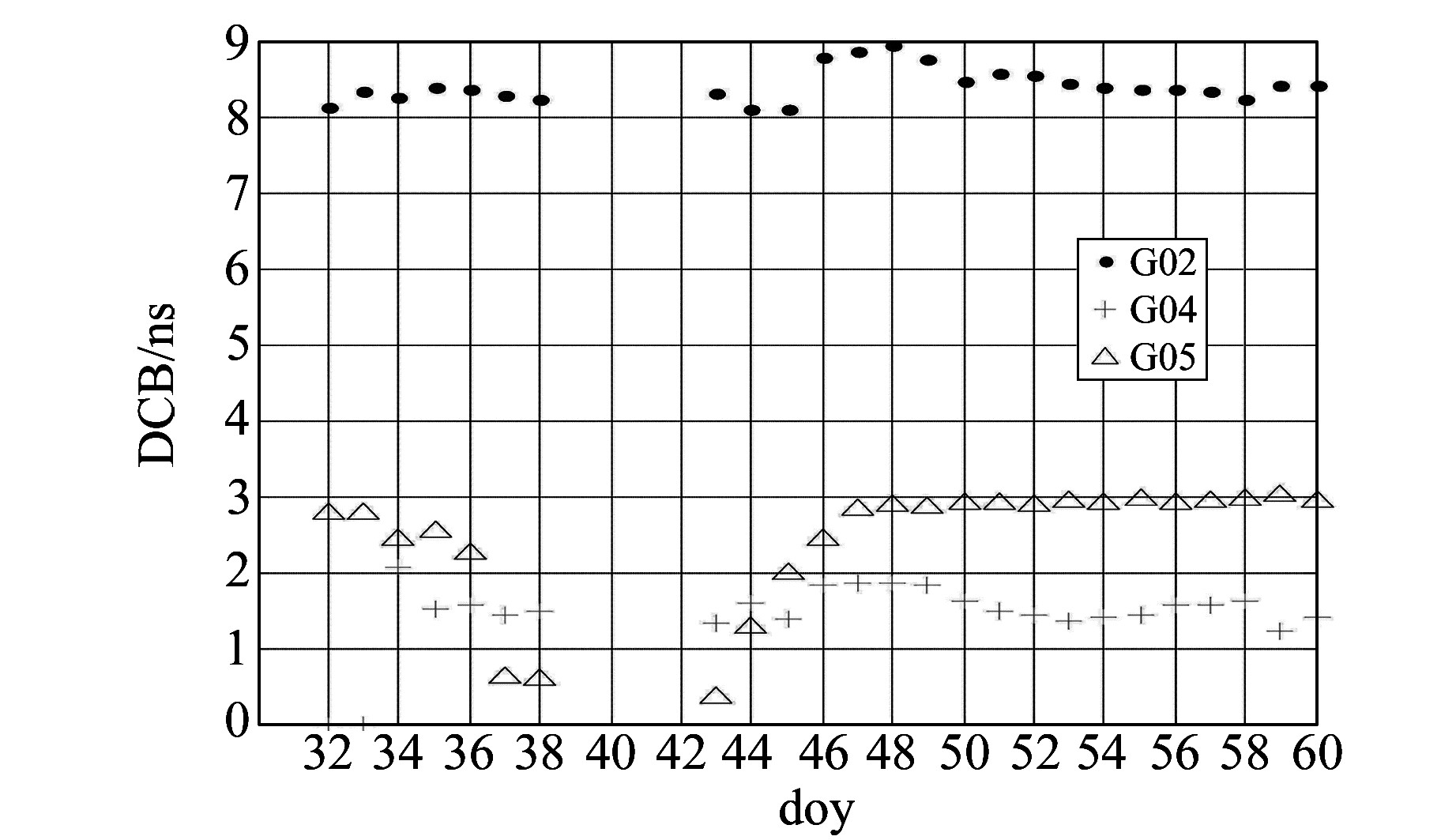
图 11 CAS最终GIM中2、4、5号GPS卫星在2016年第32~60 d的DCB序列 Fig. 11 The GPS satelites(PRN2, 4, 5) DCB series of final GIM products from doy 32 to 60 in 2016 of CAS |
|
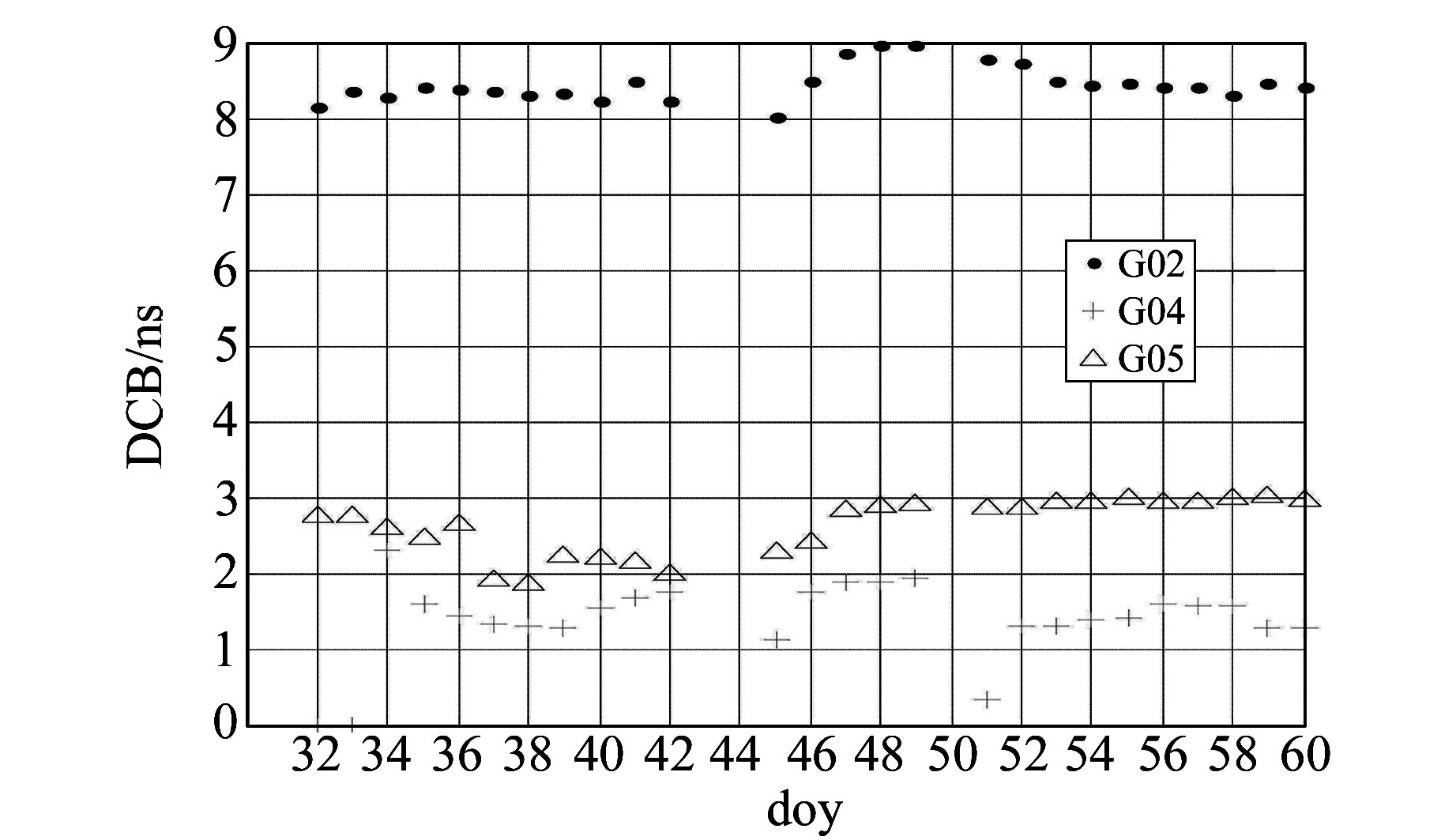
图 12 CAS快速GIM中2、4、5号GPS卫星在2016年第32~60 d的DCB序列 Fig. 12 The GPS satelites(PRN2, 4, 5) DCB series of rapid GIM products from doy 32 to 60 in 2016 of CAS |
|
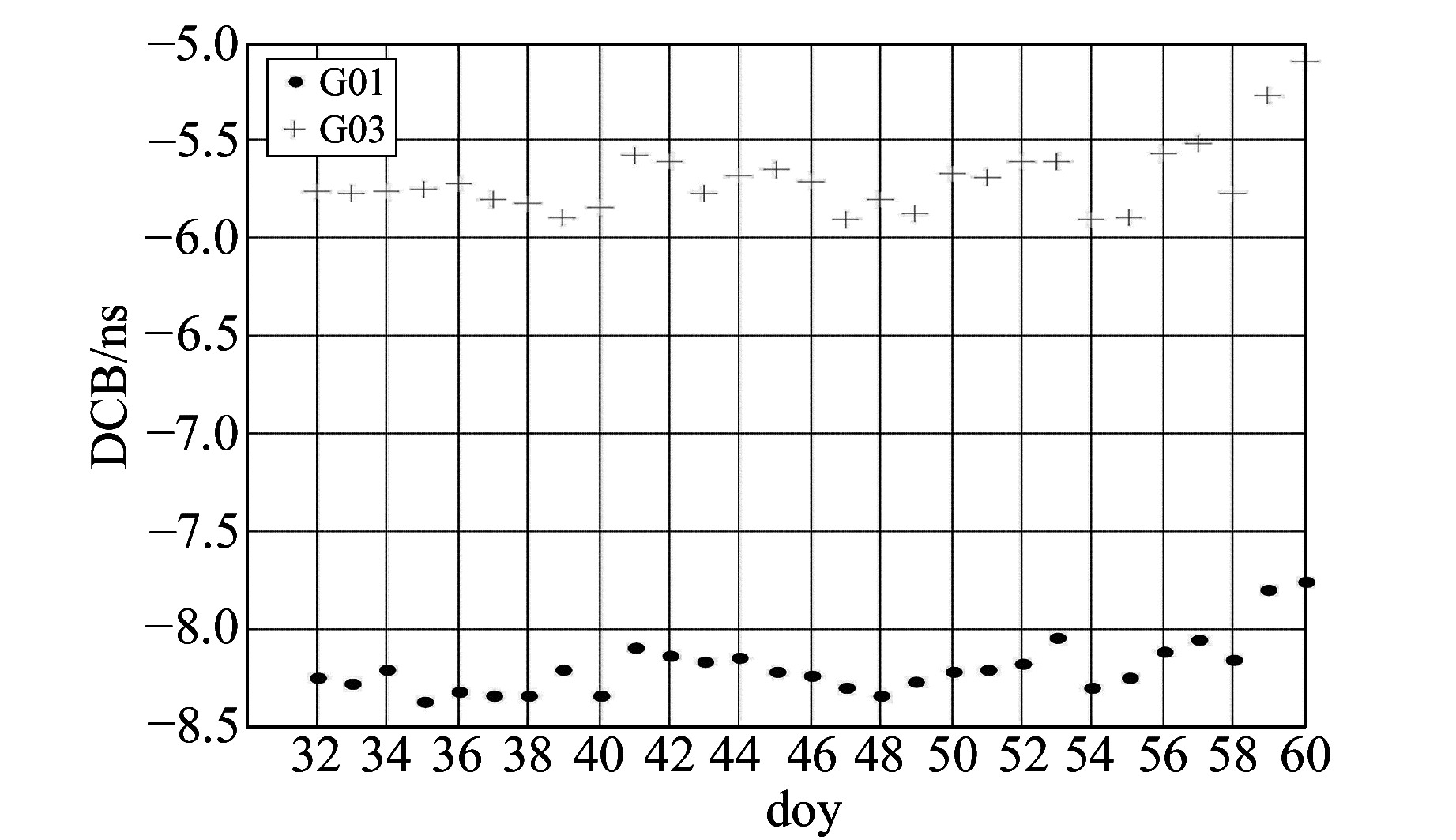
图 13 ESA最终GIM中1/3号GPS卫星在2016年第32~60 d的DCB序列 Fig. 13 The GPS satelites(PRN1、3) DCB series of final GIM products from doy 32 to 60 in 2016 of ESA |
|
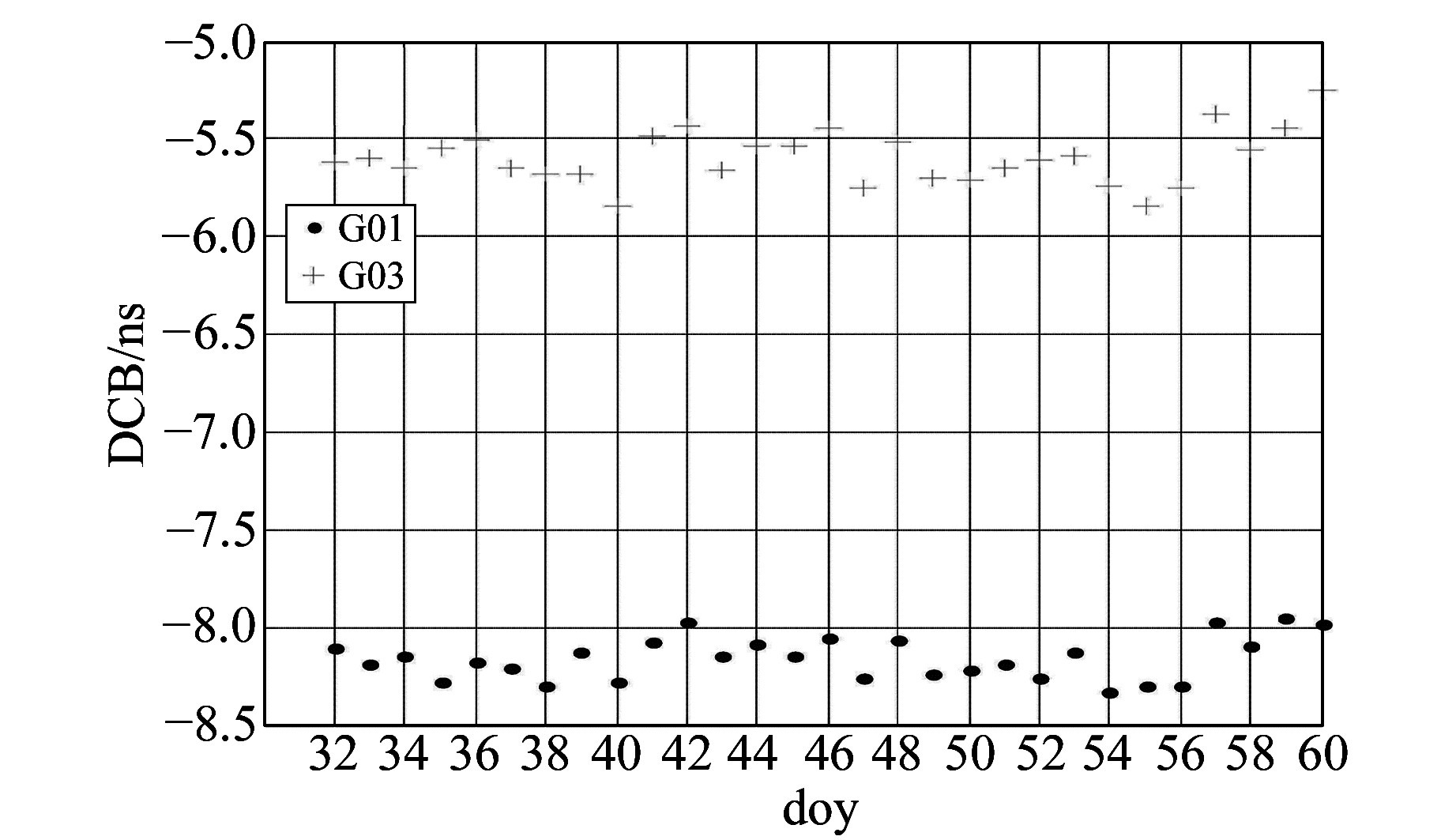
图 14 ESA快速GIM中1、3号GPS卫星在2016年第32~60 d的DCB序列 Fig. 14 The GPS satelites(PRN1, 3) DCB series of rapid GIM products from doy 32 to 60 in 2016 of ESA |
从图 11可以看出,CAS最终GIM中,2号和4号GPS卫星DCB虽有一定幅度的变化,但均稳定在1 ns内,其中在32、33 d 4号GPS卫星DCB为0,是因为该卫星在解算时被剔除了;而5号GPS卫星DCB在第37、38、43、44 d的解算值明显有问题。从图 12可看出,CAS快速GIM中,2号GPS卫星DCB均稳定在1 ns; 4号GPS卫星DCB在第51 d明显有问题;5号GPS卫星DCB在第37 d和38 d存在问题。CAS机构解算的2、4、5号GPS卫星DCB与其他机构的差异除了解算原因外,不排除是因为约束条件不同而引起的。
从图 13和14可以看出,ESA机构解算的最终和快速GIM中1/3号GPS卫星DCB除个别天外,变化幅度均稳定在0.5 ns内。由此看来,该机构与其他机构的1/3号GPS卫星DCB的微小差异,不是因为解算错误引起,而可能与自身的解算策略有关。
1) 无论是最终GIM,还是快速GIM,各机构的大部分GLONASS卫星的一致性比较好,并且各机构的最终GIM和快速GIM之间的一致性也比较好。
2) CAS机构在最终和快速GIM中13、15、16、19号GLONASS卫星的DCB与其他机构有一定差异。为了进一步分析,绘制了该机构在最终和快速GIM中这4颗GLONASS卫星的DCB时间序列,如图 15、16所示。
|
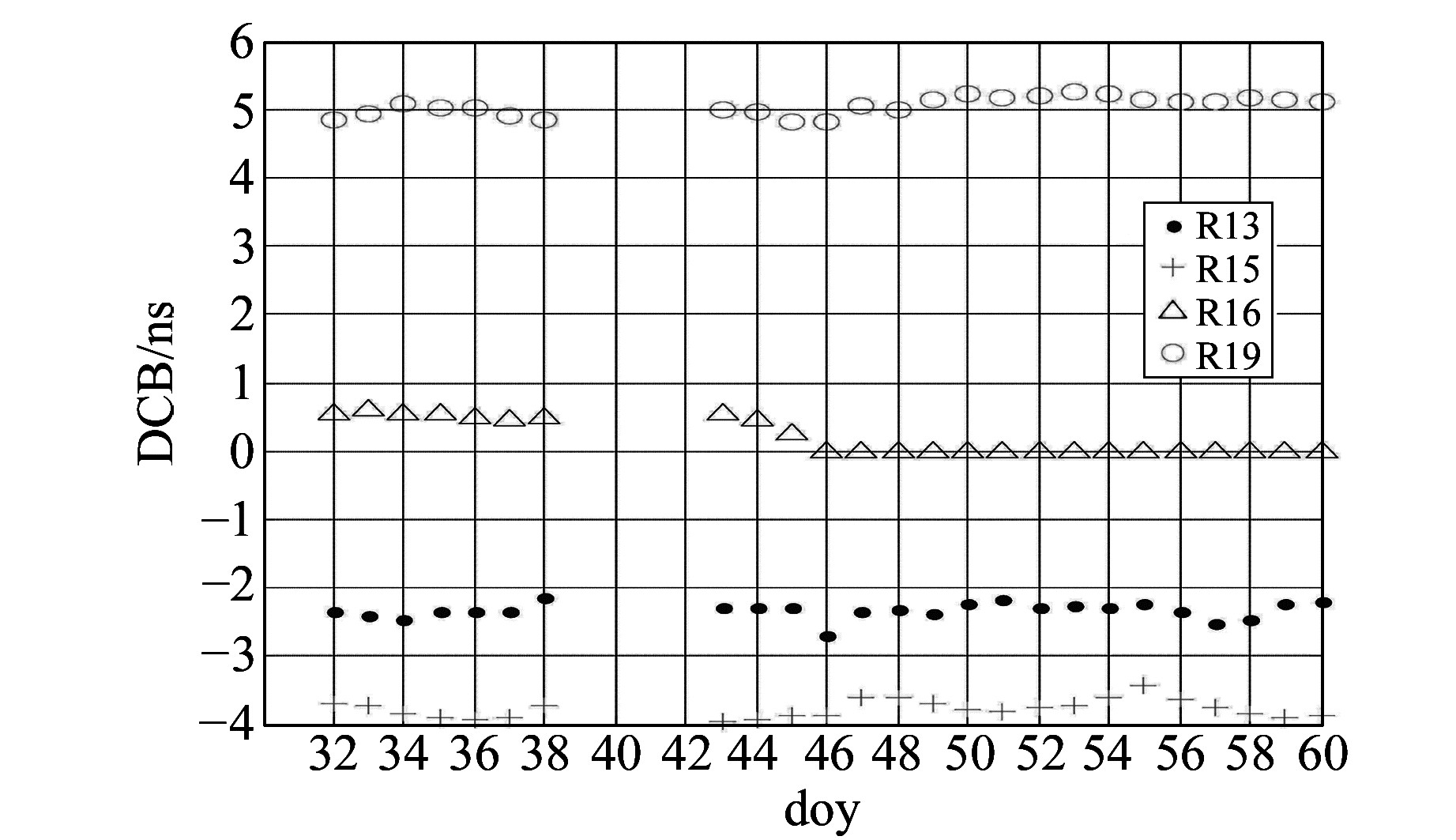
图 15 CAS最终GIM中13、15、16、19号GLONASS卫星在2016年第32~60 d的DCB序列 Fig. 15 The GLONASS satelites(PRN13, 15, 16, 19) DCB series of final GIM products from doy 32 to 60 in 2016 of CAS |
|
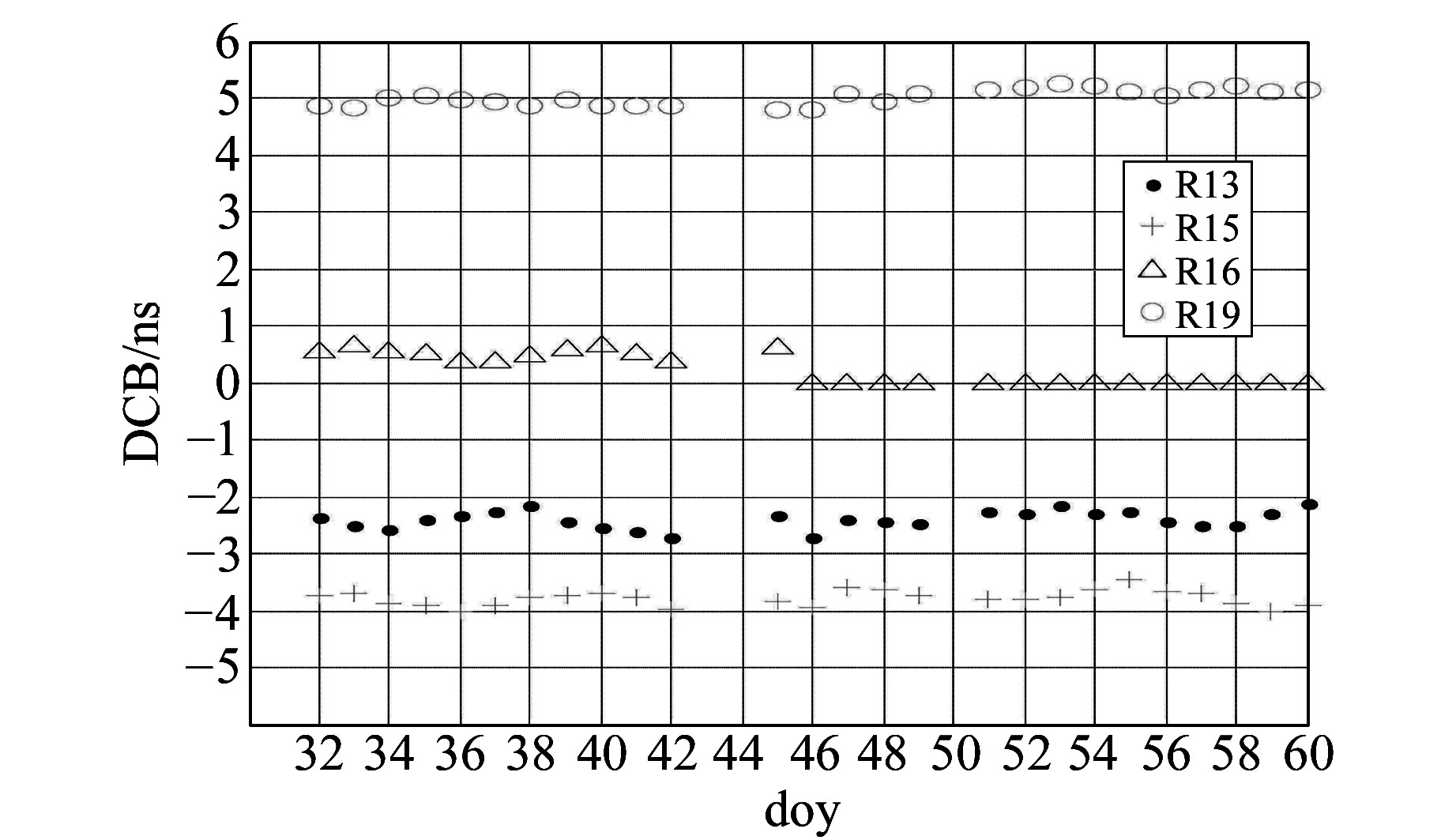
图 16 CAS快速GIM中13、15、16、19号GLONASS卫星在2016年第32~60 d的DCB序列 Fig. 16 The GLONASS satelites(PRN13, 15, 16, 19) DCB series of rapid GIM products from doy 32 to 60 in 2016 of CAS |
|
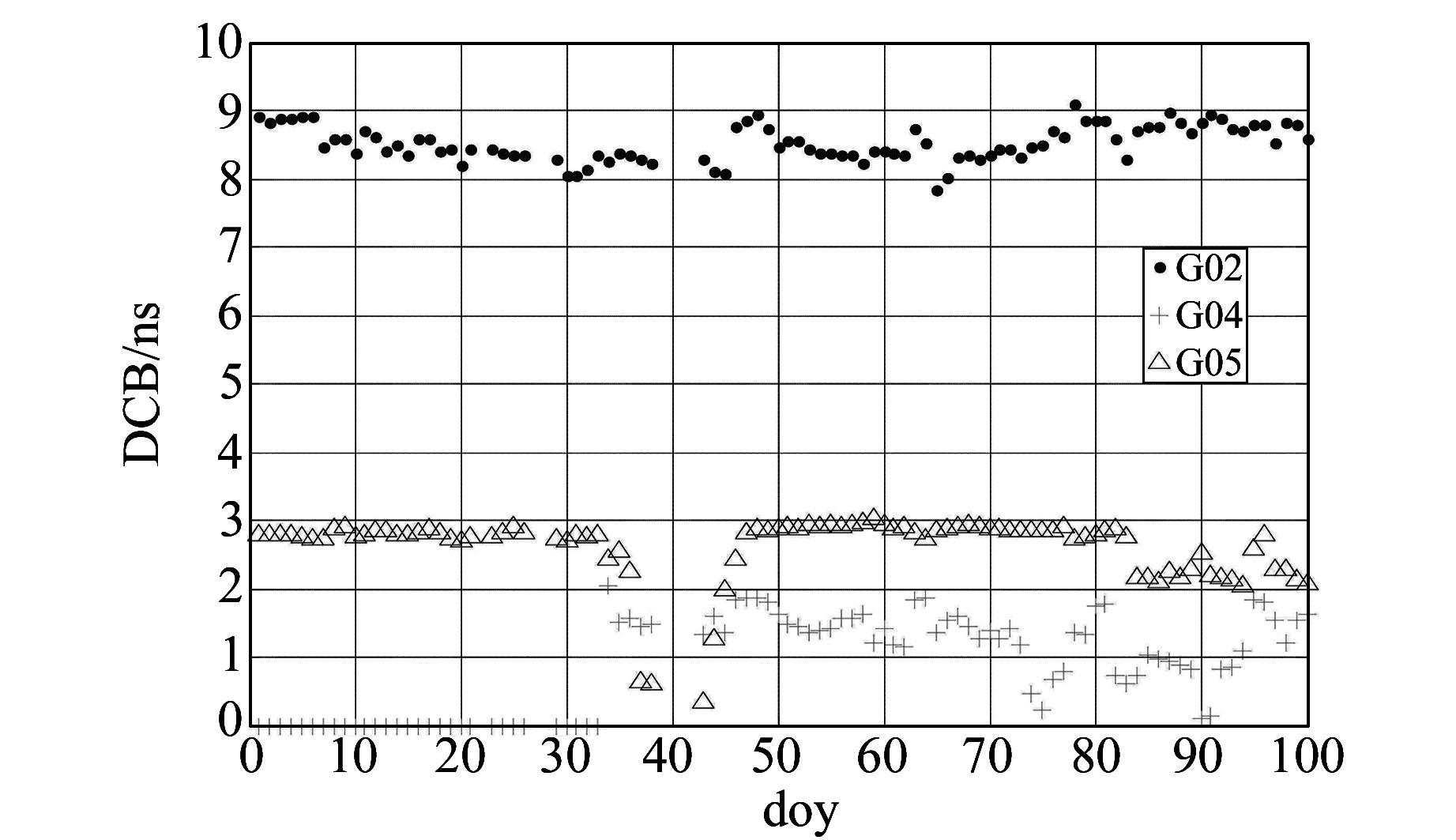
图 17 CAS最终GIM中2、4、5号GPS卫星在2016年第1~100 d的DCB Fig. 17 The GPS satelites(PRN2, 4, 5) DCB series of final GIM products from doy 1 to 100 in 2016 of CAS |
从图 15和16中可看出,CAS机构解算的最终和快速GIM中13、15、16、19号GLONASS卫星DCB变化幅度基本稳定在0.5 ns内。由此看出,CAS机构与其他机构在这几颗GLONASS卫星DCB的差异,不是因为解算错误所引起,而可能与约束条件有关。
3 结语本文分析了各机构GIM的VTEC内符合精度,同时对GIM中卫星DCB信息也作了统计分析。得到以下结论:
1) 对于最终GIM,在高纬度地区,JPL的GIM比较好,STD为1.76 TECu;在中纬度地区,CODE的GIM比较好,STD为1.78 TECu;在低纬度地区,CODE的GIM比较好,STD为2.84 TECu。
2) 对于快速GIM,在高纬度地区,JPL的GIM较好,STD为1.77 TECu;在中纬度地区,也是JPL的GIM比较好,STD为1.91 TECu;在低纬度地区,JPL和iGMAS的GIM比较好,STD均为3.14 TECu。
3) 对于CODE的预报GIM,在高纬度地区,预报1 d的GIM要优于预报2 d的GIM;在中纬和低纬度地区,两种预报GIM精度相当。
4) 无论是最终、快速还是预报GIM,随着纬度的降低,各机构的GIM精度也降低,并且各机构的GIM在低纬度地区的精度要比高纬和中纬度地区的精度低很多, 一般STD差值都在1 TECu以上,而高纬和中纬度地区的STD差值一般都在0.5 TECu以内。
5) 大部分机构的最终GIM要比快速GIM精度好一些,并且预报的GIM明显要比最终和快速GIM精度低一些。
6) 在部分纬度带,CAS机构存在快速GIM精度要比最终GIM精度要好的异常现象;同时,CAS机构在部分天,解算的4、5号GPS卫星的DCB明显存在错误。
7) CAS机构解算的2号GPS卫星DCB,变化幅度达1 ns,精度偏差;GAS机构解算的13、15、16、19号GLONASS卫星的DCB,也与其他机构的解存在一定的偏差;ESA机构解算的1、3号GPS卫星DCB也存在一定偏差。
在解算基准VTEC时,采用CODE机构的DCB产品进行相应的DCB改正,可能会导致评估的CODE的GIM精度偏好,下一步将考虑采用单独的DCB产品减小这种相关性。
致谢: 感谢iGMAS、CAS以及IGS中心提供数据及技术支持。
| [1] |
Schaer S, Gurtner W, Feltens J, IONEX: The Ionospheric Map Exchange Format Verion 1[C]. IGS AC Workshop, Darmstadt, Germany, 1998
(  0) 0) |
| [2] |
陈鹏, 陈家君. 全球电离层格网模型精度影响因素分析[J]. 大地测量与地球动力学, 2014, 34(2): 105-110 (Chen Peng, Chen Jiajun. Analysis on Factors Affecting Accuracy of Global Lonospheric Grid Model[J]. Journal of Geodesy and Geodynamics, 2014, 34(2): 105-110)
(  0) 0) |
| [3] |
Xiang Y, Yuan Y, Li Z, et al. Analysis and Validation of Different Global Ionospheric Maps (GIMs) over China[J]. Advances in Space Research, 2015, 55(1): 199-210 DOI:10.1016/j.asr.2014.09.008
(  0) 0) |
| [4] |
Luo W, Liu Z, Li M. A Preliminary Evaluation of the Performance of Multiple Ionospheric Models in Low- and Mid-latitude Regions of China in 2010-2011[J]. GPS Solutions, 2014, 18(2): 297-308 DOI:10.1007/s10291-013-0330-z
(  0) 0) |
| [5] |
李征航, 张小红. 卫星导航定位新技术及高精度数据处理方法[M]. 武汉: 武汉大学出版社, 2009 (Li Zhenghang, Zhang Xiaohong. New Techniques and Precise Data Processing Methods of Satellite Navigation and Positioning[M]. Wuhan: Wuhan University Press, 2009)
(  0) 0) |
| [6] |
Li Z, Yuan Y, Wang N, et al. SHPTS: Towards a New Method For Generating Precise Global Ionospheric TEC Map Based on Spherical Harmonic and Generalized Trigonometric Series Functions[J]. Journal of Geodesy, 2015, 89(4): 331-345 DOI:10.1007/s00190-014-0778-9
(  0) 0) |
2. Xi'an Research Institute of Surveying and Mapping, 1 Mid-Yanta Road, Xi'an 710054, China;
3. Shanghai Astronmical Observatory, CAS, 80 Nandan Road, Shanghai 200030, China
 2017, Vol. 37
2017, Vol. 37