对流层延迟由对流层中干空气成分和水汽造成,是影响精密单点定位精度的主要因素之一,也是GPS气象学中重要的研究对象[1]。通常将天顶对流层延迟(zenith total delay, ZTD)分为天顶静力学延迟(zenith hydro-static delay, ZHD)与天顶湿延迟(zenith wet delay,ZWD)。于胜杰等[2]通过对GPS大气可降水量的反演研究指出,GPS测站上的ZHD估计精度在很大程度上依赖于气压参数的精度,在实际工作中必须获取高精度的气压数据。其中,利用精密气象仪器获得的实时气象数据是最佳的数据源,也可以使用NWM(numerical weather model)数据[3]。当上述两种气象数据都不能获得时,可以使用经验模型进行估算,目前国内外公认且广泛使用的经验模型主要有GPT(global pressure and temperature model)、GPT2(global pressure and temperature model 2)以及两种最新的GPT2w模型——GPT2w_5和GPT2w_1。王君刚等[4]利用全球29个IGS站以及IGS产品分析了NMF、VMF1以及GPT2模型的精度情况,得到GPT2模型相比GPT模型在全球的精度提高25%的结论,但是作者在中国境内仅使用WUHN测站进行检验,使得其结论在中国地区的符合情况受到限制;姚宜斌等[5-6]利用水平分辨率为2.5°×2.5°的ECMWF(european centre for medium-range weather forecasts)气象数据产品在全球范围内检验GPT2模型气压和气温结果的精度,指出GPT2模型具有较强的季节特性。
无线电探空技术是目前气象业务中采集气象数据最常用的工具,时间分辨率一般为12 h,每天0:00及12:00释放探空气球采集数据,能够测定气压、气温、湿度、风向和风速等气象要素[7]。一般情况下探空测量的温度可精确到0.5 K,气压可精确到1 hPa[8], 能够满足实验研究的精度要求。本文使用探空数据检验了GPT、GPT2w_5与GPT2w_1模型在中国地区的精度,并分析模型季节变化和纬度变化特征。为了更好地显示各模型计算结果的统计学特征,本文结合箱形图对数据结果进行分析。
1 GPT/GPT2w模型GPT模型是Bohm等[9]建立的气象数据估计模型。该模型使用自1999-09~2002-08 ECMWF的40 a再分析数据(ERA40),采用基于大地水准面的9阶9次球谐函数建立。其基本原理是利用年平均值和年周期振幅,以余弦函数的形式求出测站大地水准面处的气压和气温[9]:
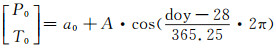
|
(1) |
式中,P0和T0分别为大地水准面处的气压和气温;doy为年积日;a0为年平均值;A为年周期振幅。分别对大气水准面处的气压和气温结果进行指数或线性高程改正,得到测站处气压和气温。GPT模型使用9阶9次球谐函数展开,分别计算气压和气温的年平均值、年周期振幅以及测站大地水准面差距等参数:
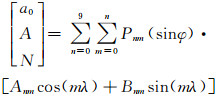
|
(2) |
式中,N为大地水准面差距;Pnm为拉格朗日多项式系数;Anm和Bnm为球谐函数系数;λ和φ分别代表测站经纬度。
GPT模型考虑了气压、气温的年周期变化,使用者仅需输入时间及坐标数据即可得到地球表面任意点处的气压、气温数据。但由于GPT模型采用9阶9次球谐函数建模,导致模型水平分辨率仅为20°×20°;仅考虑年平均值和年周期振幅参数,导致时间精度较低;另外模型采用固定的气压和气温递减率,与实际情况相比具有一定的误差[6]。针对上述问题,2013年Lagler等[10]利用2001~2010年精度更高的月均气象数据(ERA-Interim 37)重新建立了GPT2模型。该模型加入了半年周期的变化,不再基于平均海平面上的球谐函数计算参数,而是改为以5°格网的ETOPO5平均高程为基准进行计算,获得了全球水平分辨率为5°×5°的气象数据, 并将气温递减率的计算调整为每个格网处气温递减率的平均值,而且增加了干湿映射函数系数等参数的计算,模型计算公式如下:
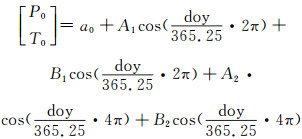
|
(3) |
式中,A1、B1为年周期参数;A2、B2为半年周期参数。
为了进一步增强模型对ZWD的估计精度,2015年Bohm在GPT2模型的基础上建立了GPT2w模型2015年Bohm在GPT2模型的基础上建立了GPT2w模型[11]。GPT2w模型以1°格网的ETOPO5平均高程为基准进行参数计算,建模数据与GPT2模型相同,但提供了5°×5°和1°×1°格网数据,并且较GPT2模型增加了大气加权平均温度和水汽压递减率的参数计算。模型将测站处大气加权平均温度和水汽压递减率结果代入Askne & Nordius公式[12]中计算ZWD。本文将GPT2w的5°×5°格网模型与1°×1°格网模型分别简称为GPT2w_5模型和GPT2w_1模型。
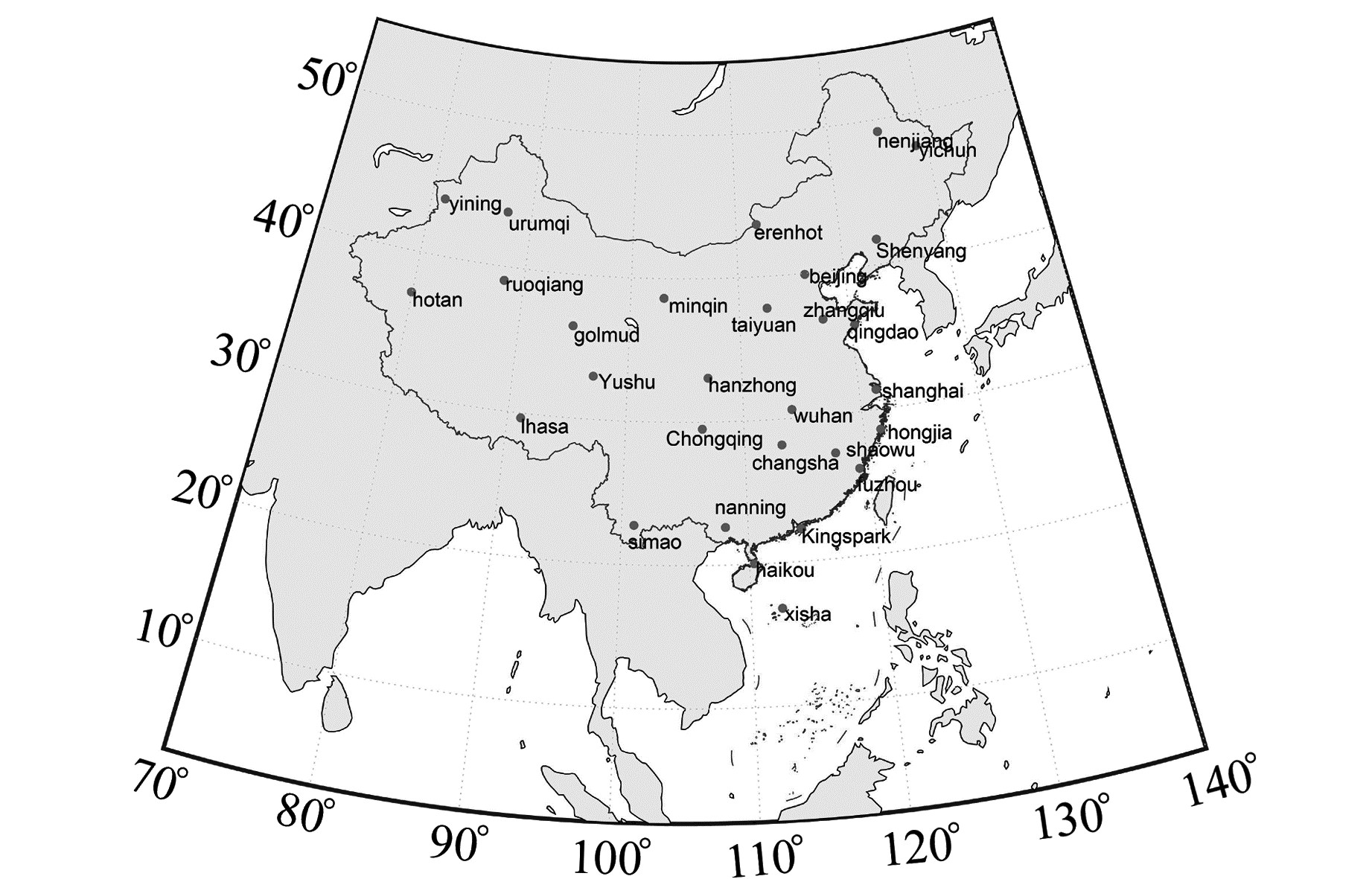
2 研究区域和数据源本文选取中国区域内29个探空气象站作为实验站点,从美国Wyoming大学气象中心下载了各站2015-03-01~2016-02-29每天12:00采集到的地面气压、气温数据作为基准数据进行实验,探空站的分布见图 1。
|
图 1 实验探空气象站分布 Fig. 1 Distribution of the radio sounding sites for experiment |
根据各测站的位置和时间信息,使用GPT、GPT2w_5和GPT2w_1模型计算得到图 1中探空站处1 a的气压、气温数据时间序列。采用均方根误差(RMS)作为精度评定标准,求出GPT模型得到的数据与相应探空数据的偏差,并计算得到每个探空站的偏差均方根误差;将29个探空站的偏差均方根误差升序排列,使用序列的中位数,上、下四分位数(序列75%及25%处)以及最小值和最大值绘制箱形图。GPT2w_5和GPT2w_1模型的数据处理过程与GPT模型相同。通过分析数据的中心、离散程度以及异常值等信息,检验3种气象模型的总体精度,讨论模型的季节性和纬度特性。
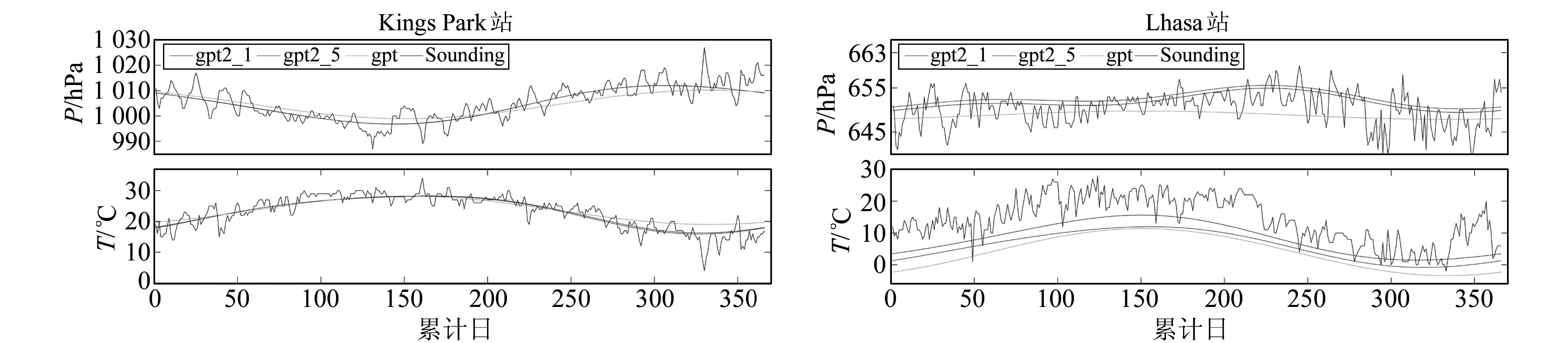
3 模型精度比较 3.1 气压、气温数据比较使用GPT、GPT2w_5和GPT2w_1模型得到了各探空站1 a的气压、气温时间序列,获得了与模型数据相对应的探空数据时间序列,并将3种模型得到的数据与探空数据进行对比。限于篇幅,这里仅给出拉萨地区的Lhasa探空站与香港地区的Kings Park探空站的对比结果,见图 2。
|
图 2 3种气象模型的气压和气温结果 Fig. 2 Results of the pressure and temperature of the three meteorological models |
由图 2可以看出,3种气象模型与探空数据的趋势具有较好的一致性,并且各模型气象参数呈现出一定的季节性。在Lhasa探空站处,3种气象模型的结果较探空数据偏差较大,但GPT2w_1和GPT2w_5模型精度较GPT模型仍有提高。其他各站情况与Kings Park站类似,3种气象模型的结果与探空数据的差异并不明显。分别计算各探空站3种模型结果与探空数据偏差的均方根误差,得到如图 3所示的箱形图。

|
图 3 3种气象模型的气压、气温偏差均方根误差 Fig. 3 RMS of the pressure and temperature of the three meteorological models |
从图 3可知,GPT2w_5与GPT2w_1模型的气压、气温偏差均方根误差整体小于GPT模型,两模型精度有明显提高。气压方面,GPT2w_5与GPT2w_1模型的偏差均方根误差中位数减小了1 hPa左右,且最小偏差均方根误差小于3 hPa;GPT2w_5与GPT2w_1模型精度相近,但是GPT2w_1模型上四分位数较GPT2w_5模型稍大。气温方面,GPT2w_5与GPT2w_1模型均方根误差的上、下四分位数差距更小,表明模型稳定性较GPT模型更高;3种模型均出现了异常值,但GPT2w_1模型的异常值与GPT模型相比较小。
3.2 随季节的变化特征根据我国季节变化特点,将研究时段分为春夏秋冬4个季节,分别对应3~5月、6~8月、9~11月以及12~次年2月。计算3种气象模型在29个探空站不同季节中气压、气温的偏差,并得到偏差均方根误差箱形图,见图 4。

|
图 4 3种气象模型的气压、气温在不同季节的偏差均方根误差 Fig. 4 RMS of pressure and temperature in different seasons of three meteorological models |
从图 4可以看出,不同季节中3种模型的偏差均方根误差有明显差异,均具有明显的季节性。气压方面,GPT2w_5及GPT2w_1模型偏差均方根误差的上、下四分位数及中位数都明显减小,精度较GPT模型明显提高;在春季GPT2w_5及GPT2w_1模型的最小偏差均方误差较GPT模型变大,且出现异常值;3种模型在夏季的精度最高。气温方面,春季GPT模型的偏差均方根误差整体偏大,最大处与最小处相差10 ℃左右,精度最差;GPT2w_5及GPT2w_1模型偏差均方根误差在各个季节均小于GPT模型。同时可以看出,3种模型均出现较多的异常值,尤其出现在冬季,但GPT2w_1模型的异常值较GPT及GPT2w_5模型更小,表现出更好的鲁棒性。
3.3 随纬度的变化特征根据我国大陆地区的纬度范围,将研究区域划分为20°~30°N、30°~40°N、40°~50°N三部分,并分别计算各模型气压、气温的偏差均方根误差,得到如图 5所示的箱形图。

|
图 5 3种气象模型气压、气温在不同纬度带的偏差均方根误差 Fig. 5 RMS of pressure and temperature in different latitude zone of three meteorological models |
由图 5可知,随着纬度的增加,3种模型的偏差均方根误差逐渐增大,模型精度逐渐降低, 表明模型受纬度影响较为显著。气压方面,在各纬度带内,GPT2w_5和GPT2w_1模型中位数以及上四分位数较GPT模型明显减小,说明模型在各纬度带内的精度均有明显的提高。气温方面,精度变化情况与气压变化基本一致,在不同纬度带内气温精度的差距较小;在20°~30°N纬度带内,3种模型中出现的一处严重异常值为Lhasa探空站,可能的原因是该站海拔较高,对模型的估计精度产生了一定影响,但GPT2w_1模型的异常值与GPT和GPT2w_5模型相比显著降低,表明GPT2w_1模型具有更好的鲁棒性。
4 结语1) 3种模型均具有季节特性,总体精度夏秋季较高,冬春季较低。
2) 3种模型对纬度的变化较为敏感,低纬度地区的估计精度最高,随着纬度的增加,精度逐渐降低。
3) 在中国地区内,GPT2w_5与GPT2w_1模型精度相当,二者的气压和气温精度较GPT模型均有明显提高,但对于个别异常值,GPT2w_1模型较GPT2w_5模型表现出更好的鲁棒性。
| [1] |
包海. GPS精密单点定位中对流层延迟改正模型的研究与分析[D]. 长沙: 中南大学, 2008 (Bao Hai. Research on the Model of Troposphere Delay Correction in GPS Precision Point Positioning[D]. Changsha: Central South University, 2008) http://cdmd.cnki.com.cn/Article/CDMD-10533-2008167746.htm
(  0) 0) |
| [2] |
于胜杰, 万蓉, 付志康. 气压对GPS大气可降水量解算的影响分析[J]. 大地测量与地球动力学, 2013, 33(2): 87-90 (Yu Shengjie, Wan Rong, Fu Zhikang. Impact Analysis of Pressure Parameter on Inversion of GPS Precipitable Water Vapor[J]. Journal of Geodesy and Geodynamics, 2013, 33(2): 87-90)
(  0) 0) |
| [3] |
Bevis M, Businger S, Herring T A. GPS Meteorology: Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System[J]. Journal of Geophysical Research:Atmospheres, 1992, 97(D14): 15 787-15 801 DOI:10.1029/92JD01517
(  0) 0) |
| [4] |
王君刚, 陈俊平, 王解先. GNSS对流层延迟映射模型分析[J]. 天文学进展, 2014, 32(3): 383-394 (Wang Jungang, Chen Junping, Wang Jiexian. Analysis of Tropospheric Propagation Delay Mapping Function Models in GNSS[J]. Progress in Astronomy, 2014, 32(3): 383-394 DOI:10.3969/j.issn.1000-8349.2014.03.07)
(  0) 0) |
| [5] |
姚宜斌, 曹娜, 许超钤, 等. GPT2模型的精度检验与分析[J]. 测绘学报, 2015, 44(7): 726-733 (Yao Yibin, Cao Na, Xu Chaoqian, et al. Accuracy Assessment and Analysis for GPT2[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(7): 726-733)
(  0) 0) |
| [6] |
姚宜斌, 张豹, 严凤, 等. 两种精化的对流层延迟改正模型[J]. 地球物理学报, 2015, 58(5): 1 492-1 501 (Yao Yibin, Zhang Bao, Yan Feng, et al. Two New Sophisticated Models for Tropospheric Delay Corrections[J]. Chinese Journal of Geophysics, 2015, 58(5): 1 492-1 501)
(  0) 0) |
| [7] |
周毓荃, 欧建军. 利用探空数据分析云垂直结构的方法及其应用研究[J]. 气象, 2010, 36(11): 50-58 (Zhou Yuquan, Ou Jianjun. The Method of Cloud Vertical Structure Analysis Using Rawinsonde Observation and Its Applied Research[J]. Meteorological Monthly, 2010, 36(11): 50-58 DOI:10.7519/j.issn.1000-0526.2010.11.008)
(  0) 0) |
| [8] |
李伟, 邢毅, 马舒庆. 国产GTS1探空仪与VAISALA公司RS92探空仪对比分析[J]. 气象, 2009, 32(10): 97-102 (Li Wei, Xing Yi, Ma Shuqing. The Analysis and Comparison between GTS1 Radiosonde Made in China and RS92 Radiosonde of Vaisala Company[J]. Meteorological Monthly, 2009, 32(10): 97-102 DOI:10.7519/j.issn.1000-0526.2009.10.012)
(  0) 0) |
| [9] |
Boehm J, Heinkelmann R, Schuh H. Short Note: A Global Model of Pressure and Temperature for Geodetic Applications[J]. Journal of Geodesy, 2007, 81(10): 679-683 DOI:10.1007/s00190-007-0135-3
(  0) 0) |
| [10] |
Lagler K, Schindelegger M, Bohm J. GPT2: Empirical Slant Delay Model for Radio Space Geodetic Technique[J]. Geophysical Research Letters, 2013, 40(6): 1 069-1 073 DOI:10.1002/grl.50288
(  0) 0) |
| [11] |
Böhm J, Möller G, Schinddegger M, et al. Development of an Improved Empirical Model for Slant Delays[J]. GPS Solutions, 2015, 19(3): 433-441 DOI:10.1007/s10291-014-0403-7
(  0) 0) |
| [12] |
Askne J, Nordius H. Estimation of Tropospheric Delay for Microwaves from Surface Weather Data[J]. Radio Science, 2016, 22(3): 379-386
(  0) 0) |
 2017, Vol. 37
2017, Vol. 37

