2. 山东科技大学测绘科学与工程学院,青岛市前湾港路579号,266510
水汽是影响降水的关键要素之一,水汽探测常用的手段有水汽辐射计、无线探空气球和卫星遥感等。地基GNSS水汽探测具有全天候连续观测、时间和空间分辨率高、成本低、精度高且不受天气条件影响的优势[1]。目前的GNSS连续观测站以大地测量为目的,因此许多测站没有配备气压和温度观测仪器,有的气象仪器长时间未使用导致记录不准确或者损坏,限制了这些观测站数据在气象领域的应用[2]。在缺少气压和温度等气象数据时,如何利用对流层延迟直接推算可降水量,许多学者对可降水量和对流层延迟、气压、温度的相关性[3-4]和模型建立[5-9]作了很多研究。但这些关于转换模型的研究仅针对短期数据建立模型,或者是对全年的数据只建立一个单一的模型(其精度比较低),而缺少对不同季节对流层延迟和可降水量的相关性分析、季节模型建立。由于不同季节可降水量的差异较大,有必要构建不同季节的GNSS对流层延迟与可降水量的转换模型。
本文对2014年桃园各季节的对流层延迟(ZTD)和可降水量(PWV)开展相关性分析,建立线性回归模型,并用2013年的数据进行验证。
1 数据获取和处理过程由于实际降水前后可降水量一般会出现骤增和骤降的过程,变化速率较大[10],所以通过查询历史天气网,把2013年的检验数据分为降水数据和无降水数据。通过NASA网站(ftp://cddis.gsfc.nasa.gov/pub/gps/)得到2014年台湾桃园(TWTF)站全年的对流层延迟、气压、温度以及三维坐标(2014年数据有缺失),2013年每个季节选取10 d降水和10 d无降水的对流层延迟、气压和温度,共80 d的检验数据,最后得到共342 d的完整数据。NASA分别提供采样率为30 s的气压值和300 s的对流层延迟值,为避免数据冗余带来计算量增加和数据过少造成计算不准确,每小时提取1个气压值和1个对流层值,计算可降水量。
GNSS可降水量的计算过程如下:1)GNSS对流层延迟直接从下载的数据中提取出来;2)根据获得的TWTF站的纬度、大地高和大气压数据,使用Saastamoinen模型计算得到静力学延迟;3)利用对流层延迟和静力学延迟的差值得出湿延迟,再乘以转换系数得到可降水量。本文采用纬度和年积日(doy)来计算转换系数[1]。
2 对流层延迟与可降水量相关性分析根据2014年的对流层延迟数据和可降水量数据作出两者之间的比较(图 1),用SPSS软件求得两者之间的相关系数、sig值(表 1)。

|
图 1 对流层延迟和可降水量比较 Fig. 1 Comparison between zenith tropospheric delay and precipitable water vapor |
|
|
表 1 4个季节和全年的对流层延迟和可降水量相关系数和sig值 Tab. 1 Correlation coefficient and sig value of zenith tropospheric delay and precipitable water vapor in the four seasons and the whole year |
图 1(d)冬季相关性图上横轴12月份(335~365 d)用-30~0 d代替。可以看出,对流层延迟和可降水量在数值上相差很大,但两者的变化趋势几乎相同。通过表 1看出,四季和全年对流层延迟和可降水量的相关系数都大于0.97,sig值都为0,显著性检验说明相关性很强,其中春季的相关系数为0.995,相关性最强;夏季的相关系数为0.973,与其他季节和全年的相关性相比,相关性最弱。
3 对流层与可降水量的线性回归模型构建与检验 3.1 模型建立由于对流层延迟与可降水量之间具有良好的相关性,因而可以对二者进行线性回归分析。设对流层延迟(ZTD)为自变量,可降水量(PWV)为因变量,线性回归方程为:

|
(1) |
式中,a、b为未知参数,ε为随机变量[11]。
回归分析的主要任务是通过多组样本观测值(ZTD,PWV)对a、b进行参数估计。一般用â和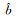

|
(2) |
为PWV关于ZTD的一元线性经验回归方程[12]。通过最小二乘的方法,得到估计值â和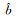
通过2014年TWTF站的对流层延迟(ZTD)和可降水量(PWV),得出全年和季节线性回归方程,其表达式分别为:
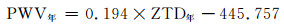
|
(3) |
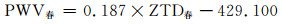
|
(4) |

|
(5) |
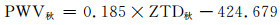
|
(6) |

|
(7) |
把2013年4个季节的降水数据和无降水数据分别代入各个季节相应的线性回归方程,把全年中所有降水和无降水数据代入全年的线性回归方程,得到的线性回归可降水量与GNSS可降水量作比较,结果见图 2,其RMS值见表 2。

|
图 2 线性回归PWV与GNSS PWV对比 Fig. 2 Comparison between linear regression PWV and GNSS PWV |
|
|
表 2 4个季节和全年降水、无降水的线性回归PWV与GNSS PWV的RMS值 Tab. 2 RMS of linear regression PWV and GNSS PWV of precipitation and nonprecipitation in the four seasons and the whole year |
从表 2可以看出,4个季节GNSS可降水量与线性回归可降水量的降水RMS值、无降水RMS值都小于1.6 mm,全年降水RMS值、无降水RMS值都小于2.1 mm。由于春季、夏季、冬季降水的天数较多,秋季无降水的天数较多,所以春季、夏季、冬季降水RMS值小于无降水RMS值,秋季降水RMS值大于无降水RMS值,表明除秋季外,春季、夏季和冬季线性回归得到的无降水结果都比降水结果好。
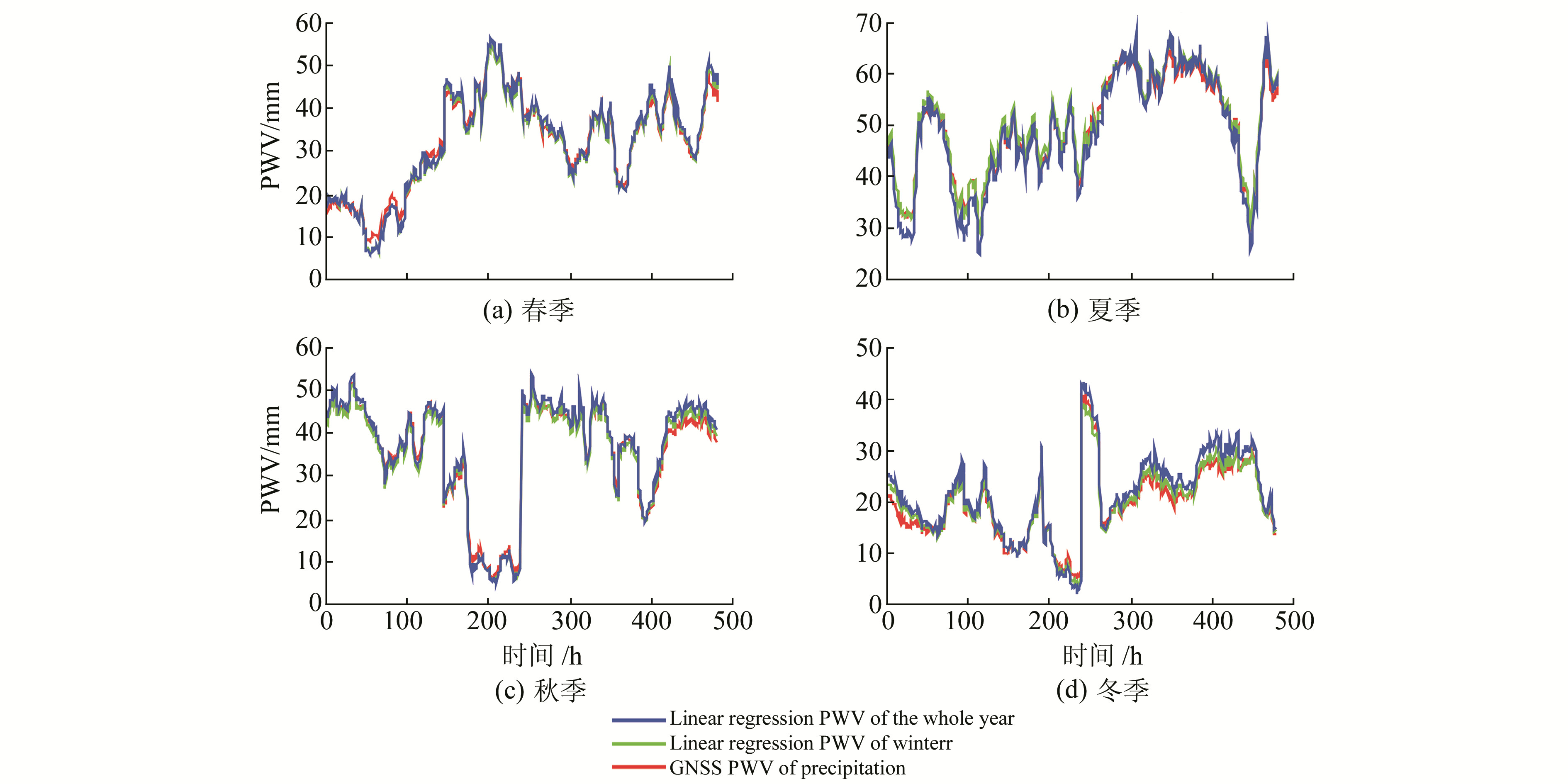
把2013年各个季节的检验数据分别代入季节和全年线性回归方程,得出的结果和GNSS可降水量作比较,如图 3和表 3所示。
|
图 3 四季、全年线性回归PWV与GNSS PWV的比较 Fig. 3 Comparison between linear regression PWV and GNSS PWV in four seasons and the whole year |
|
|
表 3 四季、全年线性回归PWV与GNSS PWV的RMS、绝对值均值、绝对值最大误差 Tab. 3 RMS, mean absolute value, absolute maximum error of linear regression PWV and GNSS PWV in four seasons and the whole year |
从图 3可以看出,季节线性回归的结果要比全年的回归结果更接近GNSS可降水量。从表 3可以看出,各季节线性回归得到的GNSS可降水量与线性回归可降水量的RMS值、绝对值均值和绝对值最大误差都比全年线性回归得到的小,各季节的RMS值都小于1.5 mm、绝对值均值都小于1.1 mm、绝对值最大误差都小于3.3 mm。全年的RMS值最大值为2.3 mm,最大的绝对值最大误差为5 mm,是季节绝对值最大误差的1.5倍左右。总体来看,各季节线性回归的效果比全年的好。
根据2013年4个季节的检验数据得到误差和绝对误差,如图 4所示。从图 4(a)可以看出,绝对误差在整体上满足正态分布;从图 4(b)可以看出,误差主要分布在0~3 mm,约占总数(1 920个)的99.53%,3~4 mm的绝对误差只有9个,占总数的0.47%。这说明模型精度较高、系统误差小、稳定性好,4个季节线性回归方程可以用于推算可降水量。

|
图 4 2013年4个季节的检验数据误差和绝对误差 Fig. 4 The histogram of the data error and the absolute error pie chart for four seasons in 2013 |
通过对TWTF站的GNSS对流层延迟和可降水量的相关性分析,建立4个季节的线性回归模型,通过检验得到如下结论:
1) 4个季节和全年对流层延迟与可降水量的相关系数分别为0.995、0.973、0.987、0.986、0.993,sig值都为0,说明两者有很好的相关性。
2) 季节线性回归的可降水量与GNSS可降水量的RMS都小于1.5 mm。
如果某些测站或某段时间缺少气象数据,可以通过各季节线性回归方程直接用对流层延迟推算可降水量,为短时间天气预报服务。
| [1] |
王勇, 刘严萍. 地基GPS气象学原理与应用研究[M]. 北京: 测绘出版社, 2012 (Wang Yong, Liu Yanping. Theory and Application of Ground-Based GPS Meteorology[M]. Beijing: Surveying and Mapping Press, 2012)
(  0) 0) |
| [2] |
江鹏. 地基GNSS探测2D/3D大气水汽分布技术研究[D]. 武汉: 武汉大学, 2014 (Jiang Peng. The Study of Retrieving 2D/3D Water Vapor Distribution Using Ground-Based GNSS Meteorology[D]. Wuhan: Wuhan University, 2014) http://cdmd.cnki.com.cn/Article/CDMD-10486-1015528773.htm
(  0) 0) |
| [3] |
余晓磊, 巫兆聪, 江万寿, 等. 武汉地区地基GPS遥感水汽与气象因子的相关性分析[J]. 地理与地理信息科学, 2012, 28(1): 55-58 (Yu Xiaolei, Wu Zhaocong, Jiang Wanshou. Regression Analysis between GPS PWV and Meteorological Factors in Wuhan[J]. Geography and Geo-Information Science, 2012, 28(1): 55-58)
(  0) 0) |
| [4] |
朱文明. 基于MODIS大气水汽的时间变化及其与气象因子的相关分析[D]. 南京: 南京师范大学, 2007 (Zhu Wenming. Temporal Variation of Atmospheric Water Vapor Based on MODIS and Its Correlation with Meteorological Factors[D]. Nanjing: Nanjing Normal University, 2007) http://cdmd.cnki.com.cn/Article/CDMD-10319-2007108231.htm
(  0) 0) |
| [5] |
王勇, 刘严萍, 柳林涛, 等. 无气象要素的GPS对流层延迟推算可降水量的研究[J]. 测绘科学, 2007, 32(3): 122-124 (Wang Yong, Liu Yanping, Liu Lintao, et al. The Study of GPS Zenith Tropospheric Delay Estimation of Non Meteorological Elements[J]. Science of Surveying and Mapping, 2007, 32(3): 122-124 DOI:10.3771/j.issn.1009-2307.2007.03.048)
(  0) 0) |
| [6] |
王勇, 刘严萍, 柳林涛, 等. 区域GPS网对流层延迟直接推算可降水量研究[J]. 热带气象学报, 2007, 23(5): 510-514 (Wang Yong, Liu Yanping, Liu Lintao, et al. The Study of Directly Calculation Precipitable Water Vapor with Zenith Tropospheric Delay of GPS Network[J]. Journal of Tropical Meteorology, 2007, 23(5): 510-514 DOI:10.3969/j.issn.1004-4965.2007.05.013)
(  0) 0) |
| [7] |
王勇, 柳林涛, 郝晓光, 等. 武汉地区GPS气象网应用研究[J]. 测绘学报, 2007, 36(2): 141-145 (Wang Yong, Liu Lintao, Hao Xiaoguang, et al. The Application Study of the GPS Meteorology Network in Wuhan Region[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(2): 141-145 DOI:10.3321/j.issn:1001-1595.2007.02.005)
(  0) 0) |
| [8] |
于胜杰, 柳林涛. 无地面温压数据的可降水量研究[J]. 大地测量与地球动力学, 2008, 28(5): 34-38 (Yu Shengjie, Liu Lintao. Study on Precipitable Water Vapor without Meteorological Data[J]. Journal of Geodesy and Geodynamics, 2008, 28(5): 34-38)
(  0) 0) |
| [9] |
曲建光, 刘基余, 韩中元. 利用天顶对流层延迟数据直接推算水汽含量的研究[J]. 武汉大学学报:信息科学版, 2005, 30(7): 625-628 (Qu Jianguang, Liu Jiyu, Han Zhongyuan. Research on the Calculating Directly Water Vapor Value Using Zenith Tropospheric Delay Data[J]. Geomatics and Information Science of Wuhan University, 2005, 30(7): 625-628)
(  0) 0) |
| [10] |
陈于, 赵遐龄, 王开通, 等. GPS天顶对流层延迟与可降水量的相关性[J]. 测绘科学, 2016(8): 1-6 (Chen Yu, Zhao Xialing, Wang Kaitong, et al. Correlation Analysis of GPS Zenith Tropospheric Delay and Precipitable Water Vapor[J]. Science of Surveying and Mapping, 2016(8): 1-6)
(  0) 0) |
| [11] |
王颉. 试验设计与SPSS应用[M]. 北京: 化学工业出版社, 2006 (Wang Jie. Experimental Design and SPSS Application[M]. Beijing: Chemical Industry Press, 2006)
(  0) 0) |
| [12] |
汪冬华. 多元统计分析与SPSS应用[M]. 上海: 华东理工大学出版社, 2010 (Wang Donghua. Multivariate Statistical Analysis and SPSS Application[M]. Shanghai: East China University of Science and Technology Press, 2010)
(  0) 0) |
2. College of Surveying Science and Engineering, Shandong University of Science and Technology, 579 Qianwangang Road, Qingdao 266510, China
 2017, Vol. 37
2017, Vol. 37





