2. 地理信息工程国家重点实验室,西安市雁塔中路1号,710054;
3. 中国天绘卫星中心,北京市,102102;
4. 信息工程大学地理空间信息学院,郑州市科学大道62号,450001
随着我国北斗系统全球卫星组网步伐的不断加快,基于三频观测的高精度快速导航定位需求越来越高。该技术的关键是模糊度的快速固定。目前研究最多的是基于三频观测的短基线模型快速固定[1]。TCAR方法是实现短基线模糊度快速解算的算法之一[2],但随着基线增长,模糊度固定成功率逐渐降低[3-4]。为此,文献[5]提出基于几何模型的改进TCAR算法,而文献[6]则将LAMBDA搜索算法引入到TCAR算法中以提高模糊度固定的成功率。而针对中长基线三频模糊度固定受电离层延迟影响较大的问题,文献[7]采用电离层延迟加权算法予以解决,文献[8]则通过构造三频载波无几何无电离层组合的方法消除电离层延迟影响。本文提出一种基于三频无几何无电离层组合快速解算中长基线模糊度的新方法,并利用北斗观测数据进行验证分析。
1 TCAR原理及分析首先,利用伪距直接固定超宽巷模糊度;利用超宽巷组合完成站星距离精化后,用超宽巷组合固定宽巷模糊度;最后运用宽巷组合实现原始频点模糊度的固定。TCAR算法的三频观测方程为:
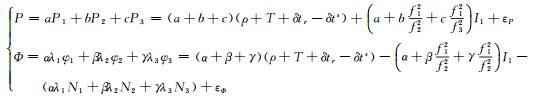
|
(1) |
式中,P为伪距,Φ为载波,a、b、c为伪距组合系数,α、β、γ为载波组合系数,ρ为站星距离,T为对流层延迟,δtr和δts分别为接收机和卫星钟差,I1为第一频点电离层延迟误差,N为模糊度,εP和εΦ分别为伪距和载波组合噪声。
三频伪距组合观测P与载波超宽巷组合φEWL差分,得到超宽巷模糊度NEWL:
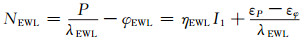
|
(2) |
若式(2)中观测误差小于λEWL/2,可直接对超宽巷模糊度取整固定。利用超宽组合替代式(2)中的伪距组合观测P,精化站星距离;通过对超宽巷组合与宽巷组合φWL差分,得到宽巷模糊度NWL表达式:
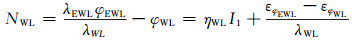
|
(3) |
式中,λWL为宽巷波长,ηWL为宽巷电离层延迟放大系数。
同样,上式观测误差小于λWL/2,即可取整固定宽巷模糊度。完成宽巷模糊度固定后,即可实现窄巷模糊度NNL的固定:
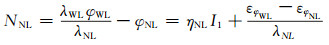
|
(4) |
式中,λNL和φNL分别为窄巷波长和观测值。
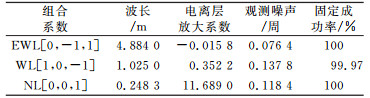
由上述步骤可知,模糊度固定主要受双差电离层残差以及伪距、载波观测噪声影响。在短基线条件下,忽略双差电离层延迟影响,仅考虑观测噪声对超宽巷、宽巷以及窄巷模糊度造成的影响。根据式(2)~(4),以模糊度固定成功率为评价标准,分析TCAR模糊度固定效果。采用文献[9]对BDS观测噪声的假设(伪距观测噪声为0.3 m,载波观测噪声为0.01周),对模糊度误差及成功率进行分析,如表 1所示。
|
|
表 1 BDS TCAR算法模糊度固定效果 Tab. 1 The ambiguity solution effect of BDS TCAR algorithm |
表 1中,超宽巷组合EWL对应的伪距观测值取值为3个频点的伪距平均值。可知,超宽巷模糊度电离层放大系数和观测噪声均相对较小,固定成功率可达100%,这主要是由于观测噪声远小于超宽巷组合波长,故影响不大。而宽巷组合受到的电离层延迟放大系数和宽巷模糊度误差影响均相对较大,固定成功率难以达到100%。短基线在忽略电离层延迟时,虽然窄巷模糊度固定成功率较高,但窄巷组合电离层延迟放大系数较大,故在较长基线或电离层活动剧烈时,电离层延迟残差将会影响窄巷模糊度固定效果。由式(2)~(4)可知,双差载波组合观测主要受大气传播延迟残差和观测噪声影响,随着基线增长,基线两端卫星轨道残差也需要考虑。下面分析随着基线增长影响模糊度固定的主要因素。设定100 km以内、100~200 km、大于200 km基线电离层延迟残差δI1分别为0.1 m、0.2 m和1 m,对流层电离层延迟残差δtro分别为0.05 m、0.10 m和0.15 m,卫星轨道误差δort分别为0.01 m、0.02 m和0.08 m(表 2),分析表 1中不同载波组合在不同长度基线条件下的模糊度固定效果。为分析观测噪声较大时的模糊度固定效果,特设置载波观测噪声δφ为0.03周。
|
|
表 2 载波虚拟观测值误差分析 Tab. 2 Error analysis of carrier virtual observation |
由表 2可知,即使在大于200 km基线电离层延迟、对流层延迟和轨道误差达到最大情况下,超宽巷模糊度误差也相对较小,仍可实现快速固定。在保证观测噪声不变的情况下,宽巷组合观测误差均由原来的0.13周(<100 km基线条件下)放大至1.212周(大于200 km基线条件下),由此说明随着基线增长,电离层延迟误差对模糊度固定的影响越来越大。进一步分析可知,当基线长度小于200 km时,宽巷模糊度误差仍相对较小,可以实现宽巷模糊度的快速固定。窄巷组合误差在100 km以内时,模糊度误差约0.7周,但随着基线增长,其模糊度误差迅速扩大到6.7周左右,其误差是其他宽巷组合的4倍多,这也进一步说明了电离层延迟误差对中长基线模糊度固定的影响较大。因此,当进行中长基线模糊度解算时,应尽量选取具备较小电离层延迟误差的宽巷组合进行模糊度解算。
2 中长基线模糊度固定中长基线超宽巷模糊度可直接进行模糊度固定,但其仍受电离层延迟误差影响。为消除该影响,本文基于三频伪距/载波无几何无电离层组合进行超宽巷模糊度固定,公式为[9]:
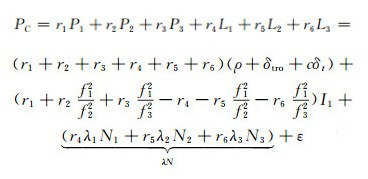
|
(5) |
式中,r1、r2和r3为对应频点伪距组合系数,r4、r5和r6为载波组合系数,λ、N分别为组合后波长和模糊度,ε表示组合后观测噪声。
为保证满足无几何无电离层组合条件,式(5)中组合系数需满足:
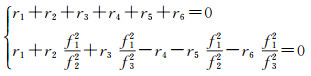
|
(6) |
假定各频点伪距观测精度相同,载波观测以周为单位的观测噪声精度亦相同,对上式模糊度误差进行分析得:
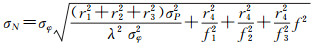
|
(7) |
式中,组合后超宽巷频率f=r4f1+r5f2+r6f3。
而对于给定的载波组合系数,要使式(7)最小,即min=r12+r22+r32。下面分析σP=0.3 m、σφ=0.01周观测条件下较优的三频伪距/载波无几何无电离层组合以及要实现大于99.9%成功率时所需要的平滑历元数n。为考虑多路径影响,计算模糊度固定成功率时,将三频伪距/载波无几何无电离层组合误差的2倍作为包括多路径效应的最终观测误差,结果如表 3所示。
|
|
表 3 BDS三频伪距/载波无几何无电离层组合 Tab. 3 BDS triple frequency pseudorange/carrier geometry free ionosphere free combination |
由表 3可知,北斗三频伪距/载波无几何无电离层组合[0, -1, 1]特性最优,其在观测条件良好时可以实现单历元的模糊度固定;而超宽巷、宽巷组合在良好观测条件下仍然能够通过数10历元平滑实现模糊度快速固定。三频伪距/载波无几何无电离层组合最多只能两个线性相关,还需找到另外一个组合,才能构成线性无关的三频模糊度组合,实现模糊度的快速解算。下面给出双差三频载波无几何无电离层组合表达式(为表达简便忽略双差符号):
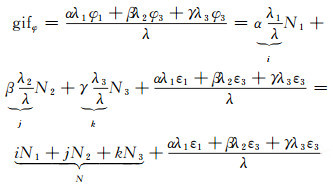
|
(8) |
式中,组合系数满足:
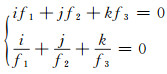
|
(9) |
式中,三频无几何无电离层组合模糊度N的误差为:

|
(10) |
根据文献[8],三频载波无几何无电离层组合可以由两个超宽巷组合观测和一个窄巷组合观测通过线性组合得到,即
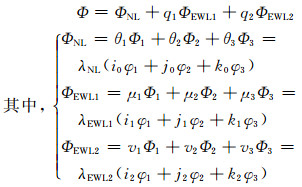
|
(11) |
式中,(i0, j0, k0)、(i1, j1, k1)和(i2, j2, k2)分别为组合中对应的载波组合系数。
根据式(8)、(9)可以得到q1和q2表达式:
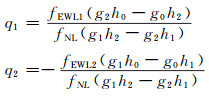
|
(12) |
式中,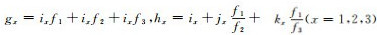
由表 2可知,超宽巷、宽巷组合系数的和为零,将该条件与式(12)代入式(11),计算窄巷模糊度方差值:
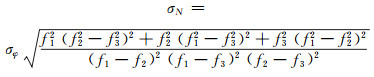
|
(13) |
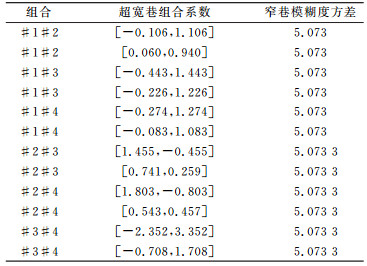
由上式可知,三频载波无几何无电离层组合中以周为单位的窄巷模糊度误差相同。假设原始载波观测噪声为0.01周,以表 3中超宽巷或宽巷组合与B2频点构造三频载波无几何无电离层组合,结果见表 4。
|
|
表 4 三频载波无几何无电离层组合 Tab. 4 Triple frequency carrier geometry free ionosphere free combination |
由表 4可知,双差窄巷模糊度误差均为5.073周,这与对式(13)的分析一致。在准确求得三频载波无几何无电离层组合值, 以及两个超宽巷组合的前提下,利用式(11)解算窄巷模糊度,利用窄巷和两个超宽巷组合构造3个频点模糊度的3个线性方程组,然后取整固定可实现模糊度的快速解算。但由表 4可知,窄巷模糊度误差较大,需要进行多历元数据平滑,才能实现整周模糊度的准确固定。
3 实验分析利用司南接收机得到的181 km基线BDS观测数据进行单历元模糊度固定。采样间隔为1 s,卫星高度角均设置为10°,分别采用TCAR算法和本文新算法进行模糊度解算。限于篇幅,实验仅对C01-C03卫星对的双差模糊度进行分析。
利用TCAR算法进行模糊度固定,实验结果如图 1所示,图中由上到下分别为超宽巷[0,-1,1]、宽巷[1,0,-1]和B2频点模糊度浮点解及其与模糊度整数真值的偏差。

|
图 1 181 km基线TCAR单历元模糊度解算 Fig. 1 Single epoch ambiguity resolution based on TCAR method of 181 km baseline |
由图 1可知,181 km基线中超宽巷双差模糊度浮点解波动范围非常小,可以实现单历元固定。双差宽巷模糊度浮点解仍能以单历元或者通过少数历元平滑实现模糊度固定,这与对表 3的分析一致。而窄巷模糊度浮点解变化范围较大,多达数周。由此可见,中长基线条件下直接对窄巷模糊度取整固定难以保证模糊度解算的准确性。对以上实测数据分析可知,长基线条件下三频宽巷、窄巷模糊度固定受电离层延迟等残差影响较大,难以实现单历元模糊度解算。而消除中长基线条件下电离层延迟等残差对宽巷、窄巷模糊度固定的影响,是实现模糊度快速固定的关键。为验证本文算法对固定中长基线模糊度的效果,同样选用上述181 km基线观测数据进行验证分析。
图 2为超宽巷组合[0,-1,1]和[1,3,-4]模糊度固定情况,其中折线为利用伪距与超宽巷载波组合差分得到的模糊度浮点解,带三角号的折线为基于三频伪距/载波无几何无电离层组合得到的模糊度浮点解。可见,两种算法得到的超宽巷组合[0,-1,1]均可实现模糊度的单历元固定,且浮点解相差不大,但基于以上两种组合得到的超宽巷组合[1,3,-4]模糊度浮点解相差数周,这是因为伪距与超宽巷组合差分得到的模糊度(图中上半部分折线所示)含有电离层延迟等残差,而伪距/载波无几何无电离层组合能够更好地消除电离层延迟,从而造成基于两种方法得到的模糊度估值出现偏差。基于三频伪距/载波无几何无电离层组合的模糊度波动范围比伪距与超宽巷载波组合的模糊度波动范围大,主要是因为在构造三频伪距/载波无几何无电离层组合时会引起伪距噪声放大。三频伪距/载波无几何无电离层组合模糊度浮点波动大,可通过历元平滑消除伪距噪声对模糊度固定的影响,但三频伪距/载波无几何无电离层组合模糊度中含有电离层延迟等系统偏差,可能会引起定位结果产生系统性偏差。由此可知,本文算法可靠性较高。

|
图 2 超宽巷模糊度固定差异 Fig. 2 Ultra wide lane ambiguity fixed |
图 3(a)为基于超宽巷组合[0,-1,1]、[1,3,-4]和窄巷[0,1,-0]构造的三频载波无几何无电离层组合观测各历元时间观测值,图 3(b)为利用式(11)解算得到的窄巷组合。可见,窄巷组合波动范围较大,波动范围接近30周,但模糊度仅受观测噪声影响,可对其进行多历元平滑以减弱观测噪声对窄巷模糊度固定的影响。

|
图 3 三频载波无几何无电离层组合解算 Fig. 3 Triple frequency carrier geometry-free ionosphere-free combination solution |
基于三频伪距/载波无几何无电离层组合得到的超宽巷模糊度更可靠,能够有效减弱中长基线电离层延迟对模糊度固定造成的影响。三频窄巷模糊度因受观测噪声影响,单历元模糊度浮点解变化较大,难以单历元固定;但其仅受观测噪声影响,可以通过一定的历元平滑实现窄巷模糊度的快速固定,进而提高中长基线模糊度解算效率。
| [1] |
Wu Z M, Bian S F, Ji B, et al. Short Baseline GPS Multi-Frequency Single-Epoch Precise Positioning: Utilizing a New Carrier Phase Combination Method[J]. GPS Solutions, 2016, 20(3): 373-384 DOI:10.1007/s10291-015-0447-3
(  0) 0) |
| [2] |
黄令勇. 三频GNSS精密定位理论与方法研究[D]. 郑州: 信息工程大学, 2015 (Huang Lingyong. Research on the Theory and Algorithm of Triple-Frequency GNSS Precise Positioning[D]. Zhengzhou: Information Engineering University, 2015) http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=chxb201512013
(  0) 0) |
| [3] |
Zhang X H, He X Y. Performance Analysis of Triple-Frequency Ambiguity Resolution with Beidou Observations[J]. GPS Solutions, 2016, 20(2): 269-281 DOI:10.1007/s10291-014-0434-0
(  0) 0) |
| [4] |
Tang W M, Deng C L, Shi C, et al. Triple-Frequency Carrier Ambiguity Resolution for Beidou Navigation Satellite System[J]. GPS Solutions, 2014, 18(3): 335-344 DOI:10.1007/s10291-013-0333-9
(  0) 0) |
| [5] |
Feng Y M. GNSS Three Carrier Ambiguity Resolution Using Ionosphere-Reduced Virtual Signals[J]. Journal of Geodesy, 2008, 82(12): 847-862 DOI:10.1007/s00190-008-0209-x
(  0) 0) |
| [6] |
刘炎炎, 叶世榕, 江鹏, 等. 基于北斗三频的短基线单历元模糊度固定[J]. 武汉大学学报:信息科学版, 2015, 40(2): 209-213 (Liu Yanyan, Ye Shirong, Jiang Peng, et al. Instantaneous Ambiguity Resolution of Short Baselines Using Beidou Triple Frequency Observations[J]. Geomatics and Information Science of Wuhan University, 2015, 40(2): 209-213)
(  0) 0) |
| [7] |
Li J, Yang Y, Xu J, et al. Ionosphere-Free Combinations for Triple-Frequency GNSS with Application in Rapid Ambiguity Resolution over Medium-Long Baselines[C]. 3th China Satellite Navigation Conference (CSNC), Guangzhou, 2012 https://link.springer.com/chapter/10.1007%2F978-3-642-29175-3_16
(  0) 0) |
| [8] |
Li B, Feng Y, Shen Y. Three Frequency Ambiguity Resolution: Distance-Independent Ambiguity Resolution Demonstrated with Semi-Generated Triple Frequency Signals[J]. GPS Solutions, 2009, 14(2): 177-184
(  0) 0) |
| [9] |
黄令勇, 翟国君, 欧阳永忠, 等. 三频GNSS电离层周跳处理研究[J]. 测绘学报, 2015, 44(7): 717-25 (Huang Lingyong, Zhai Guojun, Ouyang Yongzhong, et al. Ionospheric Cycle Slip Processing in Triple-Frequency GNSS[J]. Acta Geodaetica et Chartograpica Sinica, 2015, 44(7): 717-25)
(  0) 0) |
2. State Key Laboratory of Geo-Information Engineering, 1 Mid-Yanta Road, Xi'an 710054, China;
3. China Aerospace Surveying and Mapping Satellite Center, Beijing 102102, China;
4. School of Surveying and Mapping, Information Engineering University, 62 Kexue Road, Zhengzhou 450001, China
 2017, Vol. 37
2017, Vol. 37