2. 西部矿产资源与地质工程教育部重点实验室, 西安市雁塔路126号, 710054
PS-InSAR技术自Ferretti等[1-2]首次提出以来,在理论和应用方面均得到巨大发展,其中具有代表性的是SAR干涉点目标分析(interferometric point target analysis, IPTA)技术。该技术的改进主要体现在差分干涉及参数回归分析处理中,当SAR数据量较多时,还可以省略相位解缠步骤[3]。IPTA技术是通过对同一分区内任一PS点与给定的参考点作差分的方式建立差分相位模型,再采用二维回归分析模型进行形变和高程误差参数的求解。当研究区域较大时,为了减弱大气效应对参数估计的影响,一般先对研究区域进行分块(保证PS点与参考点之间的距离小于1 km),然后对每个PS点相位进行二维回归分析。虽然该处理能够在一定程度上减弱大气的影响,但是在PS点稀疏或者农田区域往往难以获取满意的监测结果。
由于大气延迟相位误差和外部DEM误差在空间上存在相关性[1],所以需要研究顾及相邻PS点的空间相关性,通过点间差分的方式来减弱大气与DEM误差的影响,并将参数求解的问题转化成非线性函数的最优化问题,使用该方法还可以减弱相位解缠带来的误差。
1 PS-InSAR数据预处理与差分相位模型在进行PS点建模及参数估计之前,需进行如下必要的预处理操作:1)设研究区内有N+1景SAR影像,选取其中的一景作为主影像,将其余的SAR影像配准到主影像坐标系,然后通过设置时空基线阈值进行干涉组合,可得到M幅干涉图。2)以配准后的所有SAR影像为基础,基于点目标的光谱特性和后向散射强度稳定性选取PS点。3)使用精密的轨道数据和外部DEM数据计算出对应的平地相位和地形相位,并从M幅原始的干涉图中减掉,得到对应的差分干涉相位。干涉图中每个PS点的差分干涉相位可表示成如下相位分量的总和:
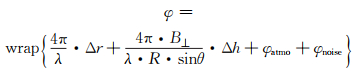
|
(1) |
式中,φ为缠绕的差分干涉相位;λ为雷达系统波长;B⊥为干涉对的垂直基线;R为PS点目标至传感器的距离;θ为雷达波入射角;Δr为两次成像期间地表在视线向发生的位移量,包括线性形变量和非线性形变量;Δh为DEM误差;φatmo为大气延迟相位;φnoise为噪声相位。
2 PS基线网络与参数估计 2.1 PS基线的识别在PS-InSAR数据处理中,通常基于经典的Delaunay剖分算法来建立PS基线网络。采用Matlab工具箱中的Delaunay函数对所有PS点进行构网时,生成的三角形记录表不仅记录了组成每个三角形的3个PS点目标的点号,同时它还隐含着PS基线边的信息,但是其中可能包含有重复边的信息。在PS-InSAR数据处理时,既要从生成的三角形记录表中识别出所有的PS基线,又得对重复基线边进行检测与剔除。本文采用邻接矩阵模型对PS基线边识别与重复边检测[4-5],以提高基线网络布设和信息存储的效率。
2.2 PS基线网络的建立与参数估计通过邻接矩阵模型识别出的PS基线边所对应的相位实际是基线边两端PS点间的差分相位的再次作差。结合式(1),假设第i个差分干涉图中某一基线边由PS点(xl, yl)和(xp, yp)构成,则其对应的差分干涉相位可表示如下:
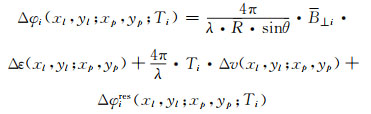
|
(2) |
对于任意PS基线边,基于M幅差分干涉图可以建立M个式(2)所示的观测方程。若式(2)左端所示的差分干涉相位Δφi的完整值已知,则采用经典的最小二乘法即可求解出各参数的估值,否则需要通过其他方法进行参数估计。
为了更好地估计线性形变速率增量和高程误差增量,定义如下目标函数:
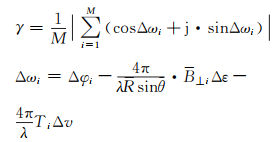
|
(3) |
式中,j为虚数单位;Δωi为观测值与模型拟合值之间的残差;γ为基线的模型相关系数,其模|γ|可以用来衡量观测值与模型的匹配程度。
基于式(2)与(3),即可求出所有PS基线边的线性形变速率增量、高程误差增量及对应的模型相关系数,然后以求解出的线性形变速率增量和高程误差增量为观测值,PS点的线性形变速率和高程误差为参数,对应的模型相关系数为权,采用加权最小二乘法得到每个PS点目标的线性形变速率和高程误差,至此就完成了研究区PS基线网络的构建与参数估计。
3 实验验证与结果分析 3.1 模拟实验为了验证本文算法的可靠性,选用太原地区2009-03~2010-03期间29景X波段TerraSAR数据的相关参数进行分析,共模拟了73个干涉对。线性形变速率采用Peaks函数模型进行模拟(其中正值表示朝向卫星方向,负值表示远离卫星方向),大气延迟相位和DEM误差都是由二维分形表面生成[6]。另外对每个干涉图施加均值为0、相位标准差为0.1 rad的高斯噪声,PS点位置采用随机模拟器产生,共模拟2 000个像素点作为PS点目标,并采用图 1(a)和1(b)所示的两种方式构建PS基线网络。

|
图 1 PS点构网示意图 Fig. 1 Network diagram of PS points |
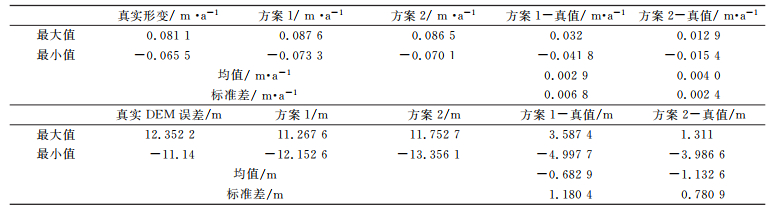
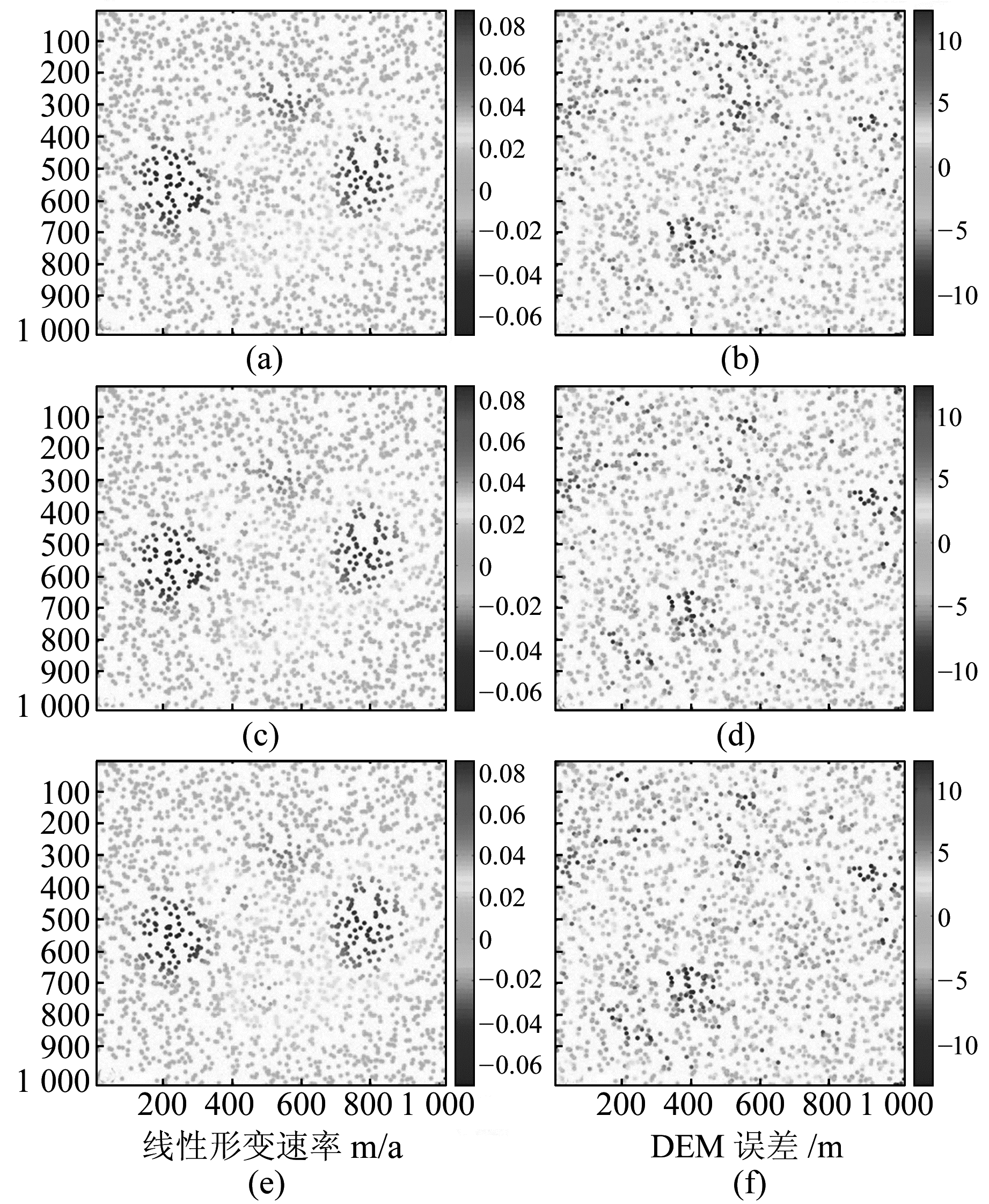
基于73个模拟的差分干涉图,使用2.2节所述的PS基线网络计算程序获取每个PS点上的线性形变速率和DEM误差改正,图 2分别为真实的及按图 1方案获取的线性形变速率和DEM误差。从图 2((a)和(b)为模拟的真值,(c)和(d)为GAMMA IPTA结果,(e)和(f)为本文算法结果)可以清楚地看出,两种方案得到的线性形变速率和DEM误差与模拟的真实形变场在空间分布上具有较好的一致性。为了评价上述两种方案获得的监测结果的精度,图 3((a)和(b)为GAMMA IPTA结果与真值的差异,(c)和(d)为本文算法结果与真值的差异)显示了两种方案获取的结果与真值之间的差值,并对差值进行分析,见表 1。从图 3可以看出,基于邻域差分的PS基线网络模型(方案2)相比常规的GAMMA IPTA技术(方案1)能够获得更好的解算结果,绝大多数PS点的估计值与真值之间的差异较小,尤其是在形变速率较小的位置。从表 1统计结果来看,方案1与方案2获取的线性形变速率与真值的差值的标准差分别为0.006 8 m/a和0.002 4 m/a,获取的DEM误差与真值的差值的标准差分别为1.180 4 m和0.780 9 m。图 3和表 1均表明,基于邻域差分的PS基线网络模型获取的形变速率及DEM误差与模拟的真值具有更高的一致性,从而证实了PS基线网络算法和计算程序的可靠性。
|
图 2 PS点的线性形变速率和DEM误差 Fig. 2 Linear deformation rate and DEM error of PS point |

|
图 3 PS点的线性形变速率和DEM误差与真值之间的差异 Fig. 3 Differences between the calculated results and true of linear deformation rate and DEM error |
|
|
表 1 两种方案获取结果与真值差异统计 Tab. 1 Statistics of the differences between the calculated results and true values |
大同-西安高速铁路穿过了太原盆地内的多条地裂缝区域,对其进行形变监测显得尤为重要。为此,本文采用覆盖太谷-祁县区域自2015-07~2016-02的8景X波段TerraSAR数据,选取长度为28.5 km的太谷-祁县段高铁沿线为研究对象,开展基于PS基线网络的高铁沿线形变监测实验。
首先以已配准的SLC影像为基础,基于点目标的光谱特性和后向散射强度稳定性共选取205 754个PS点目标,然后将8景SLC数据进行自由组合,并利用30 m分辨率的SRTM高程数据去除地形相位,最后共生成28个差分干涉对。图 4所示为基于Delaunay三角剖分算法构建的PS基线网络。可以看出,PS基线网络中存在较长的基线边,在后续处理中对长度大于200 m的基线边进行剔除。当基线边长大于200 m时,认为邻近PS点之间大气延迟相位的空间相关性将会减弱。最后利用PS基线网络计算程序获取所有PS点上的年平均沉降速率。同时,本文还采用GAMMA IPTA技术按照图 1(a)所示的构网方式对28个差分干涉相位进行二维回归分析,获取了相应的年平均沉降速率图。

|
图 4 高铁沿线PS点构成的基线网络 Fig. 4 PS network along the high speed railway |
图 5(a)和5(b)分别为GAMMA IPTA技术和本文算法获取的2015-07~2016-02太谷-祁县段高铁沿线的年平均沉降结果。对两种方案获取的结果进行对比分析:1)两种方案获取的视线向形变速率基本分布在-10~10 mm/a之间,说明在监测时段内研究区的地表形变速率较小。2)从图 5(b)可以看出,在东观变电站附近(黑色虚线框所示)存在-20 mm/a的视线向地表形变,投影到垂直方向约为-22 mm/a,与文献[7]中所述的地裂缝两侧的垂直位错约为3 cm/a,具有较好的一致性;而图 5(a)并未揭示出相似的形变特征,其原因可能是由于大气效应等影响使得PS点与给定参考点之间的相位差值超过了π,导致相位存在整周模糊度,利用二维回归分析求解时并没有恢复出真实的形变相位,而采用附加距离限制的Delaunay三角网进行PS基线网络的布设, 有效地减弱了大气相位等误差的影响,使得获取的结果更加真实。3)虽然本文方法获取的结果相对于IPTA结果存在着异常上升区域(图中蓝色区域),但是这些区域正好是IPTA解算中由于大气延迟效应等影响使得PS点的残差不满足给定的阈值条件而被舍弃的区域(如图 6所示)。初步分析异常上升的原因, 可能是差分干涉相位中存在着粗差。但对于整个高铁沿线的形变结果而言,本文算法获取的年平均沉降速率优于GAMMA IPTA技术获取的结果。

|
图 5 高铁沿线的年平均沉降 Fig. 5 Deformation rate along the high speed railway |

|
图 6 东观变电站区域的年平均形变速率 Fig. 6 Deformation rate in Dongguan substations (a)和(b)分别为图 5(a)和(b)虚线框区域的放大显示图, (c)和(d)为野外实地调查照片 |
为了更好地分析高铁沿线的地面沉降与地裂缝的空间对应关系,图 6(a)和(b)显示了两种方案对应的东观变电站区域放大显示后的年平均形变速率图,并叠加了对应的地裂缝分布信息。可以清楚地看出,GAMMA IPTA技术并未获取到地裂缝区域高铁沿线形变;而本文算法却获取了高铁沿线的形变信息,形变区主要位于路基有砟轨道上,高架无砟轨道沿线的形变相对较小。另外,在东观变电站地裂缝的两侧存在明显的差异性形变,形变主要发生在地裂缝的南侧,其位置与量级都与已有地裂缝调查资料[7]和野外实地考察资料(图 6(c)和(d))具有较好的一致性,证明本文算法用于高铁沿线形变监测的可行性与可靠性。
4 结语本文通过模拟数据和真实SAR数据对常规干涉点目标分析技术和基于邻域差分的PS基线网络获取的形变监测结果进行对比分析。相比常规的干涉点目标分析技术,基于邻域差分的PS基线网络可有效克服或减弱差分干涉相位中空间自相关的大气延迟效应等影响。本文采用该技术开展了太谷-祁县段高铁沿线的形变监测,提取了2015-07~2016-02的年平均沉降速率,发现东观变电站地裂缝与高铁相交的区域存在地面沉降现象。该结果与已有的地质资料和野外调查资料具有较高的一致性。
| [1] |
Ferretti A, Prati C, Rocca F. Permanent Scatterers in SAR Interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(1): 8-19 DOI:10.1109/36.898661
(  0) 0) |
| [2] |
Ferretti A, Prati C, Rocca F. Non-Linear Subsidence Rate Estimation Using Permanent Scatterers in Differential SAR Interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 38(5): 2202-2212
(  0) 0) |
| [3] |
Werner C, Wegmuller U, Strozzi T, et al. Interferometric Point Target Analysis for Deformation Mapping[C]. Geoscience and Remote Sensing Symposium, IEEE, Toulouse, 2003, 7: 4362-4364 https://www.researchgate.net/publication/4064847_Interferometric_Point_Target_Analysis_for_Deformation_Mapping
(  0) 0) |
| [4] |
刘国祥, 陈强, 丁晓利. 基于雷达干涉永久散射体网络探测地表形变的算法与实验结果[J]. 测绘学报, 2007, 36(1): 13-18 (Liu Guoxiang, Chen Qiang, Ding Xiaoli. Detecting Ground Deformation with Permanent-Scatter Network in Radar Interferometry: Algorithm and Testing Results[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(1): 13-18 DOI:10.3321/j.issn:1001-1595.2007.01.003)
(  0) 0) |
| [5] |
陈强, 丁晓利, 刘国祥, 等. 雷达干涉PS网络的基线识别与解算方法[J]. 地球物理学报, 2009, 52(9): 2229-2236 (Chen Qiang, Ding Xiaoli, Liu Guoxiang, et al. Baseline Recognition and Parameter Estimation of Persistent-Scatter Network in Radar Interferometry[J]. Chinese Journal of Geophysics, 2009, 52(9): 2229-2236 DOI:10.3969/j.issn.0001-5733.2009.09.006)
(  0) 0) |
| [6] |
Hanssen R F. Radar Interferometry: Data Interpretation and Analysis[M]. Dordrecht: Kluwer, 2001
(  0) 0) |
| [7] |
章卫卫.大西高铁太原盆地沿线地裂缝发育特征及其危险性评价研究[D].西安: 长安大学, 2010 (Zhang Weiwei. The Study on Development Characteristic and Its Hazard Evaluation of Ground Fissures among the Da-Xi Express Railway in Taiyuan Basin[D]. Xi'an: Chang'an University, 2010) http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1729833
(  0) 0) |
2. Key Laboratory of Western Mineral Resources and Geological Engineering, Ministry of Education, 126 Yanta Road, Xi'an 710054, China
 2017, Vol. 37
2017, Vol. 37