2. 中国科学院大学,北京市玉泉路甲19号,100049;
3. 中国地震台网中心,北京市三里河南横街5号,100045;
4. 中国地震局地震研究所(地震大地测量重点实验室),武汉市洪山侧路40号,430071
目前,单历元模糊度固定和实时数据处理成为GNSS应用于实时变形监测的前提条件。将GNSS应用于边坡监测,可提供重要的边坡变形数据[1]。我国自主研制的BDS正处于建设和发展阶段,由于星座构成和数据质量等方面的原因,BDS单系统定位效果不如GPS[2-3]。而在边坡监测中,目前BDS主要由GEO卫星和IGSO卫星组成,可以提供更稳定的观测量。因此,比较和分析单频BDS和GPS在边坡监测中的效果,具有重要应用价值和科学意义。
本文首先介绍单历元模糊度固定算法研究现状,并在GPS阻尼LAMBDA算法基础上进行扩展,详细论述了BDS/GPS双系统单频单历元阻尼LAMBDA算法原理。以该算法为基础,结合无线通信和计算机技术,实现一种实时远程GNSS变形监测系统。以四川理县某边坡监测工程为例,分析其应用效果。
1 BDS/GPS单历元定位算法对于短基线相对定位,卫星轨道误差、卫星钟差、接收机钟差、大气延迟等误差源能够通过双差很好地消除。伪距和载波相位观测方程为:
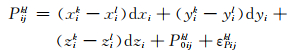
|
(1) |
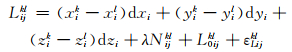
|
(2) |
式中,下标i、j为测站,上标k、l为观测卫星;P、L分别为伪距观测值和载波相位观测值;x、y、z为直角坐标系下的三维方向余弦,dx、dy、dz为相应的坐标改正数;λ、N为载波相位波长和整周模糊度;P0、L0为线性化所采用的近似值;εP、εL为伪距和载波相位观测噪声。
在相对定位中,根据观测数据类型,单历元模糊度固定算法可分为双频单历元算法和单频单历元算法。双频单历元算法有两种解算策略:1)使用双频伪距和相位观测值,计算得到模糊度浮点解,并根据LAMBDA算法或者其他搜索方法确定模糊度整数解[4];2)使用双频数据构造宽巷组合,先固定宽巷模糊度得到精度较高的坐标解,进一步固定双频整周模糊度[5]。另外,双频单历元算法可利用双频整周模糊度之间的线性关系缩小模糊度搜索范围,用于提高模糊度固定成功率[4-5]。单频单历元算法使用单频伪距和相位观测数据计算得到模糊度浮点解,由于伪距精度差且观测量少,计算得到的坐标误差通常大于1 m,导致模糊度搜索范围过大。传统的单频单历元模糊度固定所需计算时间较长,且成功率不高。
本文采用单频单历元阻尼LAMBDA算法[6],基于单频相位观测值和先验坐标约束进行单历元相对定位。在GPS阻尼LAMBDA算法基础上引入BDS系统观测量,BDS/GPS组合系统载波相位观测方程矩阵表达式为:
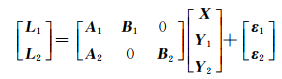
|
(3) |
式中,下标1、2分别代表BDS和GPS系统;A为坐标参数设计矩阵,与接收机和卫星的空间关系有关;B为模糊度参数设计矩阵,为单位阵;X为坐标参数向量; Y为模糊度参数向量; ε为相位观测噪声向量。
在BDS/GPS组合相对定位解算时,需考虑两个系统之间的时空基准不同和频率差异。BDS和GPS均采用周和周内秒形式的原子时,两者起算历元不同,相差1 356周又14 s[7]。对于空间基准,BDS采用的CGS2000椭球参数和GPS使用的WGS84椭球参数在mm级相对定位时可认为基本一致[8]。由于BDS的B1和GPS的L1载波相位频率不同,两个系统之间的相位观测值差分需要考虑频率差异以及模型化ISB参数[9]。本文采用标准双差算法,BDS与GPS各自设置不同的参考卫星[3]。零基线实验证明,两个系统的载波相位观测值精度相当,BDS和GPS观测量对应的权阵P1和P2(式(5))应设为不相关且等权[2]。对观测方程进行最小二乘运算,单历元BDS/GPS相对定位法方程为:
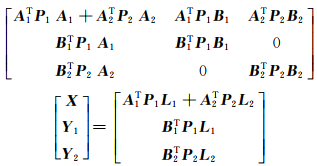
|
(4) |
由于观测方程中模糊度参数个数与双差观测值数目一致,3个坐标未知数使得模型中参数个数大于观测值个数,法方程系数阵秩亏,无法直接求逆。阻尼LAMBDA算法在法方程坐标参数X所对应的分块系数阵中加入阻尼因子阵PX(式(6)),使法方程系数矩阵满秩。使用最小二乘解算非线性问题时,需根据坐标近似值将其线性化。此时,阻尼因子阵PX代表近似坐标的先验权阵,该矩阵可由观测噪声和先验坐标精度定义。由单频相位观测方程和阻尼因子阵计算得到模糊度浮点解和协方差阵,然后通过LAMBDA算法提供的整周模糊度建立模糊度搜索空间,根据残差平方和最小原则确定整周模糊度参数,进而得到模糊度固定的单历元相对定位结果[6]。当先验坐标或者由伪距计算得到的坐标精度优于0.5 m且给出合理的坐标约束时,采用最小二乘和LAMBDA算法确定的模糊度和坐标参数是最优估值。
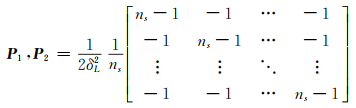
|
(5) |
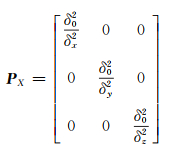
|
(6) |
式(5)、(6)中,δL2为载波相位观测值方差;ns为观测卫星数;δ02为单位权方差;δx2、δy2、δz2分别为x、y、z坐标先验方差。
2 BDS/GPS实时变形监测系统本文基于阻尼LAMBDA算法实现一种GNSS变形监测系统,其硬件部分主要包括BDS/GPS双系统单频接收机、用于无线网络数据传输的GPRS(general packet radio service,通用分组无线服务技术)DTU(data transfer unit,数据传输模块)、供电设备以及服务器和用户端等。系统软件部分主要包括搭载在服务器上的变形监测软件和WEB服务器程序。根据其工作原理,可分为数据采集部分、服务器部分和用户部分。
数据采集部分包括BDS/GPS接收机、GPRS DTU和供电设备。选择在具有代表性且观测环境相对较好的地段布设连续监测站。数据传输模块通过串口读取接收机数据,并将观测数据和卫星星历经过GPRS无线网络发送到远程的服务器。服务器部分包括服务器计算机以及运行在它上面的变形监测软件和WEB服务器程序。其中,变形监测软件是该系统的枢纽以及核心组成部分。该软件使用C/C++编写,基本功能模块包括网络数据接收与发送、RTCM解码、观测数据同化、单历元定位解算、多路径效应滤波、变形监测信息可视化以及数据库存储。WEB服务器程序主要由Tomcat和Java实现,基于WebSocket实现用户端与服务器端的全双工通信[10]。通过数据库API,WEB服务器与变形监测软件建立链接并将监测结果和变形预警信息发布给用户端。用户端为PC或者其他上网设备,经过授权后可以通过浏览器实时获取系统发布的监测结果和变形预警信息。
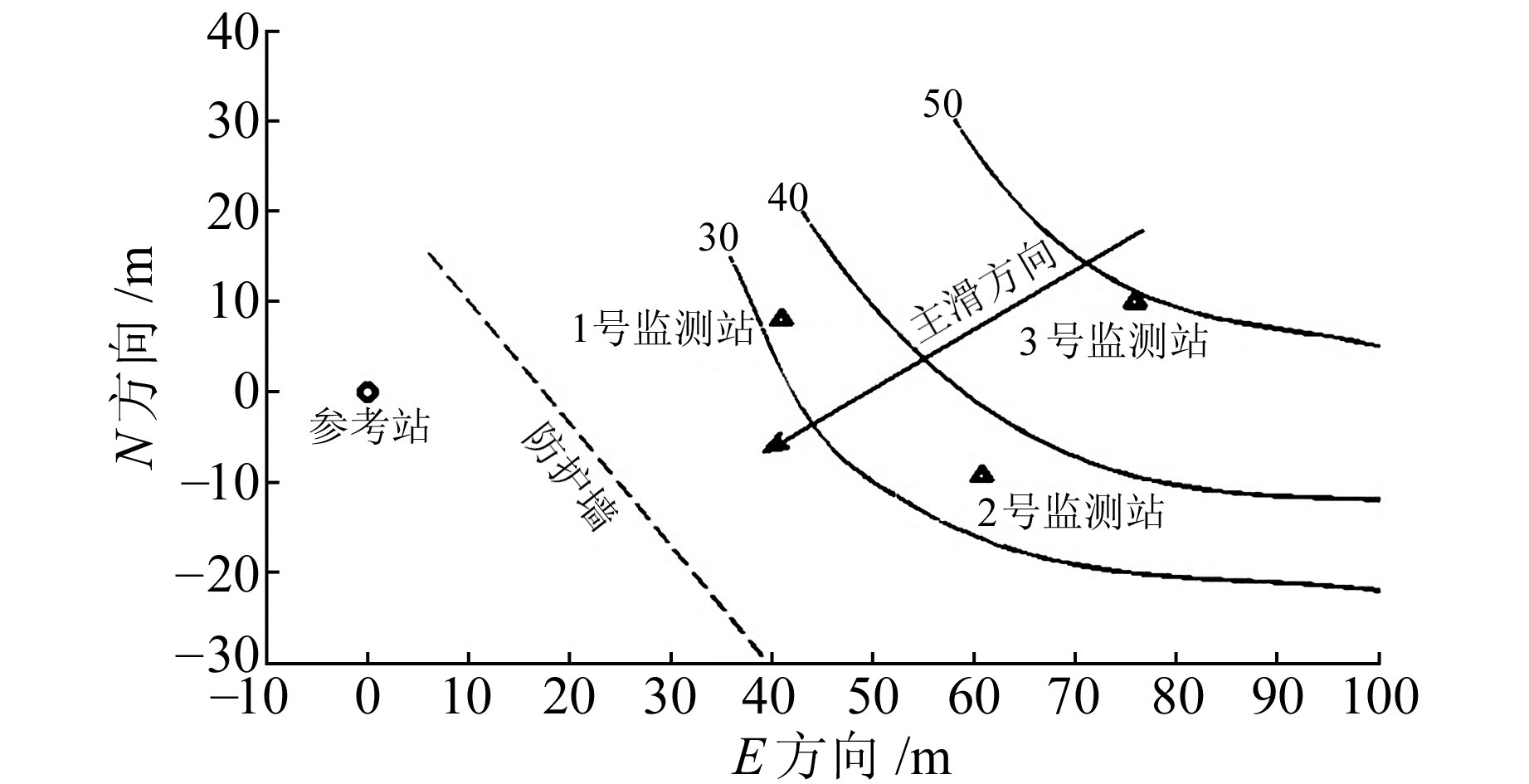
3 边坡监测效果分析 3.1 理县边坡概况四川理县某边坡位于31.50°N、103.27°E,山体面向西南方向,坡度约32°,主滑方向约245°,土方量约18万m3,属于土质边坡。由于边坡已发生明显滑动痕迹,威胁到附近居民生命财产安全,当地政府于2014年修建防护墙。本文介绍的变形监测系统也于同一时段开始对该边坡进行长期连续观测,在易滑坡山体选取3个具有代表性的地段布设监测站,并在山脚下小学教学楼顶布设参考站。以参考站为坐标原点建立局部坐标系,参考站高程设为20 m,易滑坡山体和观测站分布情况见图 1(曲线为等高线)。
|
图 1 理县边坡BDS/GPS连续观测站分布 Fig. 1 Continuous BDS/GPS observation stations in the Lixian slope |
变形监测系统使用司南导航生产的K500板卡接收机和AT330测量型天线。选取1号监测站和参考站构成的基线进行处理和分析。具体解算策略如下:监测站位于边坡,受周围植被影响,多路径效应严重,设置截止高度角为20°;监测站与基准站之间距离小于100 m,忽略电离层延迟影响;基线两端最大高差约30 m,使用Neil模型进行对流层延迟差异改正;由于天线类型一致,不考虑两个天线的相位偏差和天线相位变化差异;结合数据传输效率和实际需求,采样间隔设为5 s;模糊度固定ratio阈值为2.0。
由于边坡变形缓慢,监测站在短时间内可认为是静止,以该时间段内BDS/GPS组合系统静态定位结果为参考值,对所有历元的坐标偏差进行精度评定。统计2015年doy 282(1 865周,GPS时)04:00~06:00 BDS和GPS可见卫星数和PDOP值(图 2),BDS、GPS及其组合系统下的单历元阻尼LAMBDA算法定位坐标偏差及模糊度固定成功率(图 3、表 1)。

|
图 2 GPS、BDS以及BDS/GPS组合系统观测卫星数与PDOP值对比 Fig. 2 Comparison of observed satellite numbers and PDOP values of GPS, BDS and BDS/GPS |
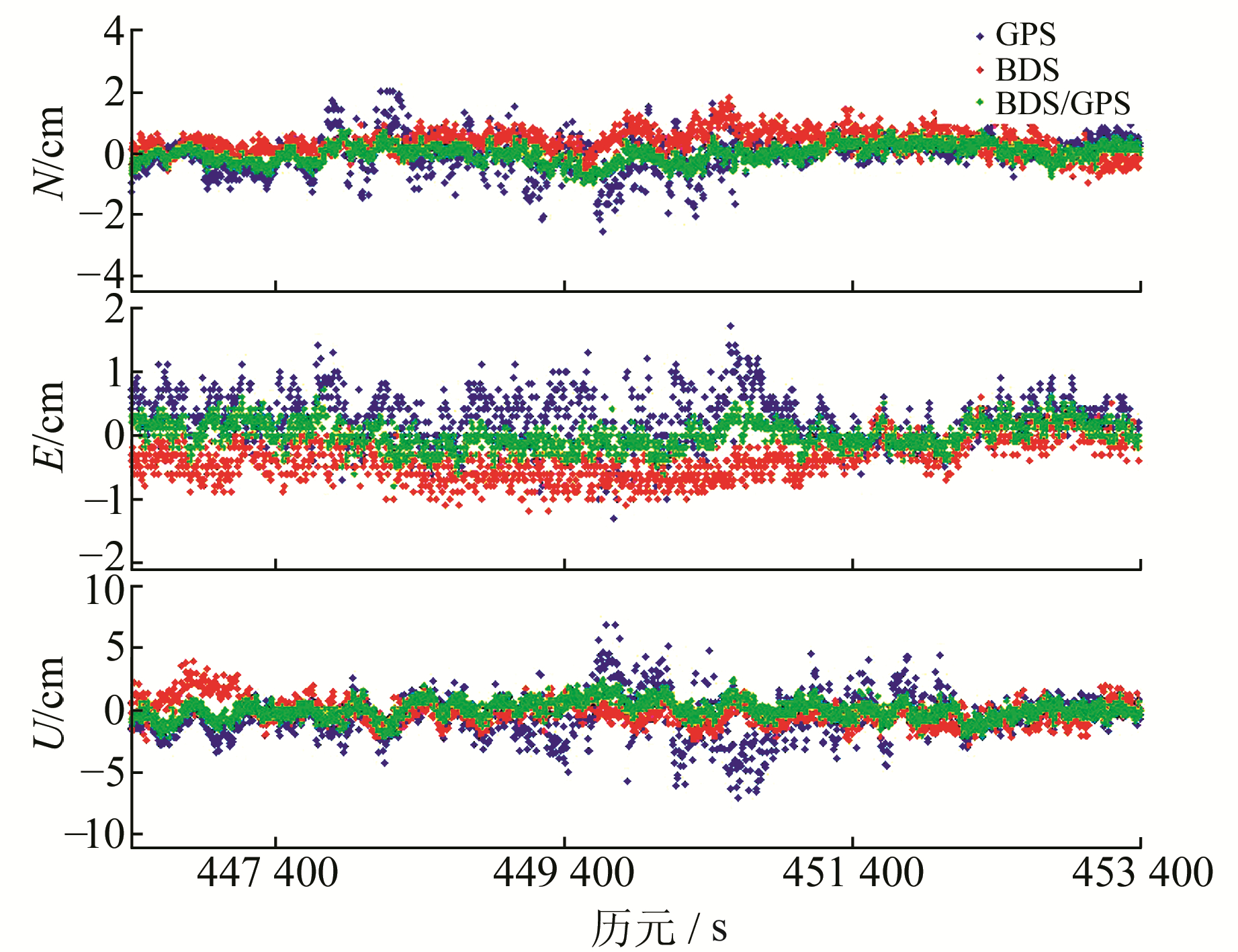
|
图 3 GPS、BDS以及BDS/GPS组合系统下单历元阻尼LAMBDA定位结果对比 Fig. 3 Comparison of positioning results of GPS, BDS and BDS/GPS using single epoch damped LAMBDA algorithm |
|
|
表 1 不同卫星系统下定位结果标准差 Tab. 1 Standard deviation of positioning results using different satellite systems |
从图 2可以看出,在整个观测时间段内,BDS平均观测卫星数为7~8,GPS平均观测卫星数为4~5,单系统解算时BDS比GPS观测卫星数更多。BDS与GPS平均PDOP值均为4.8。与GPS相比,BDS的PDOP值在大部分时间内更稳定。而组合系统在该时间段内一直保持卫星数大于11,PDOP值小于3.7,观测条件明显优于BDS和GPS单系统。图 3和表 1表明,在单系统定位效果方面,BDS在N、E、U方向上的标准差要明显优于GPS,尤其是U方向,优势更为显著。BDS单系统下的定位时间序列在整个时间段内比较稳定,而GPS解算的坐标时间序列在447 450 s~451 480 s之间波动较大。模糊度固定成功率方面,BDS也比GPS高8%左右。BDS/GPS组合系统定位效果优于BDS和GPS单系统,N、E、U方向标准差分别提高了48%、45%、56%以及20%、29%、23%,模糊度固定成功率与BDS单系统相当。
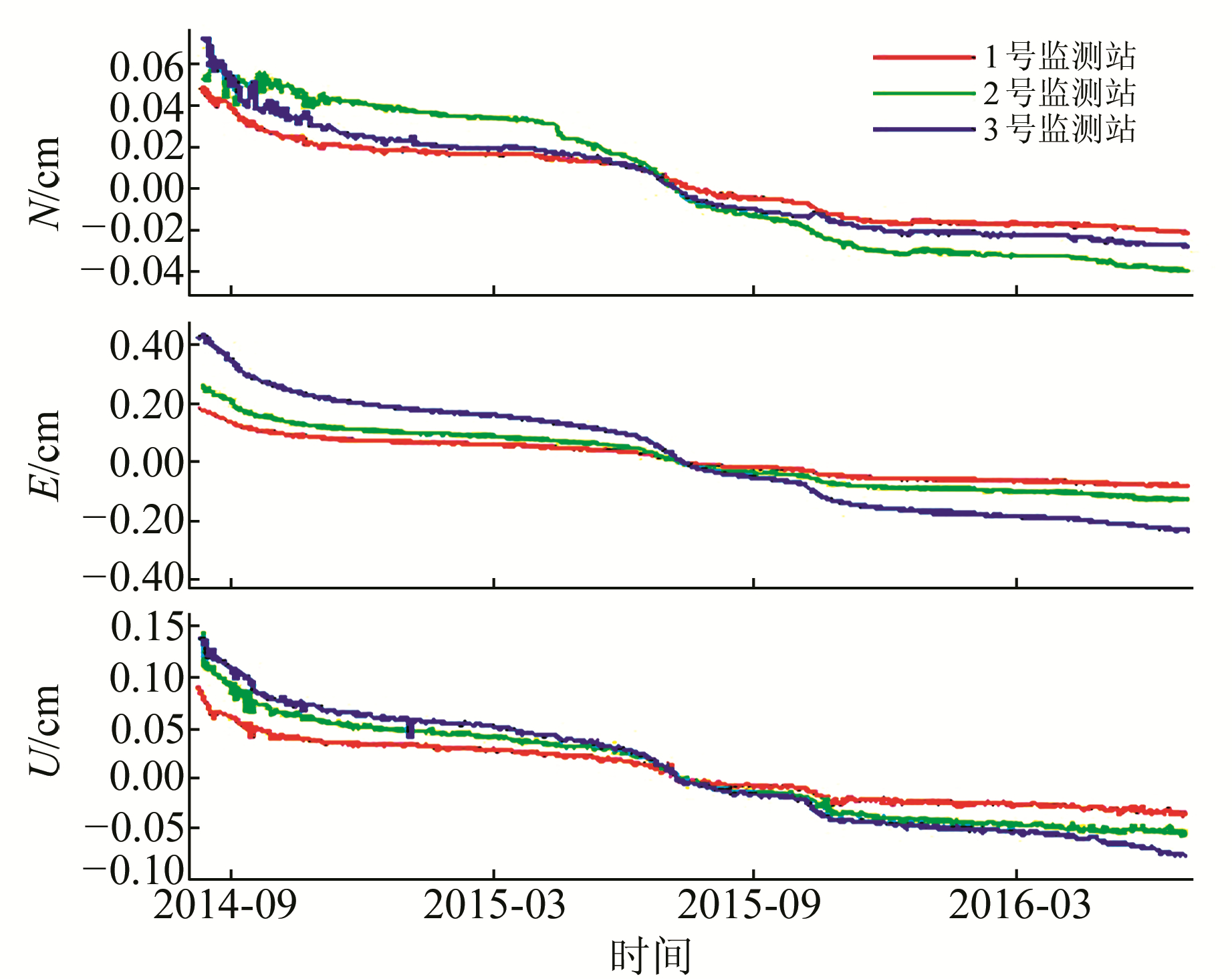
3.3 长期位移与降雨量相关性分析变形监测系统于2014-08-19开始在理县边坡运行,目前已得到3个测站长达23个月的位移序列。长期观测表明,在N、E、U三个方向上,1号监测站位移量为6.90 cm、26.30 cm、12.60 cm,2号监测站位移量为9.20 cm、39.20 cm、20.00 cm,3号监测站位移量为10.00 cm、65.40 cm、21.50 cm,平均位移量分别为8.70 cm、43.63 cm、18.03 cm,如图 4。3个监测站位移速率基本一致,且呈现出一定的季节性趋势,在雨季(每年的5月到10月)变化速率较快,在旱季(每年的11月到4月)变化较慢。
|
图 4 扣除均值后的理县边坡3个监测站的长期位移趋势 Fig. 4 Long-term displacements (deducted the average) of the three monitoring stations in the Lixian slope |
从中国气象数据网下载距理县边坡最近的马尔康、松潘和温江3个气象站2014-08-19~2015-06-30的历史降雨量,3个气象站分别距理县103 km、140 km、99 km,使用这3个气象站的日降雨数据,依据距离加权法内插出理县日降雨量。由变形监测系统得到的边坡位移序列计算累积位移量,并根据理县日降雨量积分得到累积降雨量。以累积降雨量达到223 mm处,对应时间为2015-02-22为界线,分段建立线性回归模型:
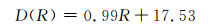
|
(7) |
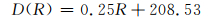
|
(8) |
式中,D为累积位移量,R为累积降雨量。
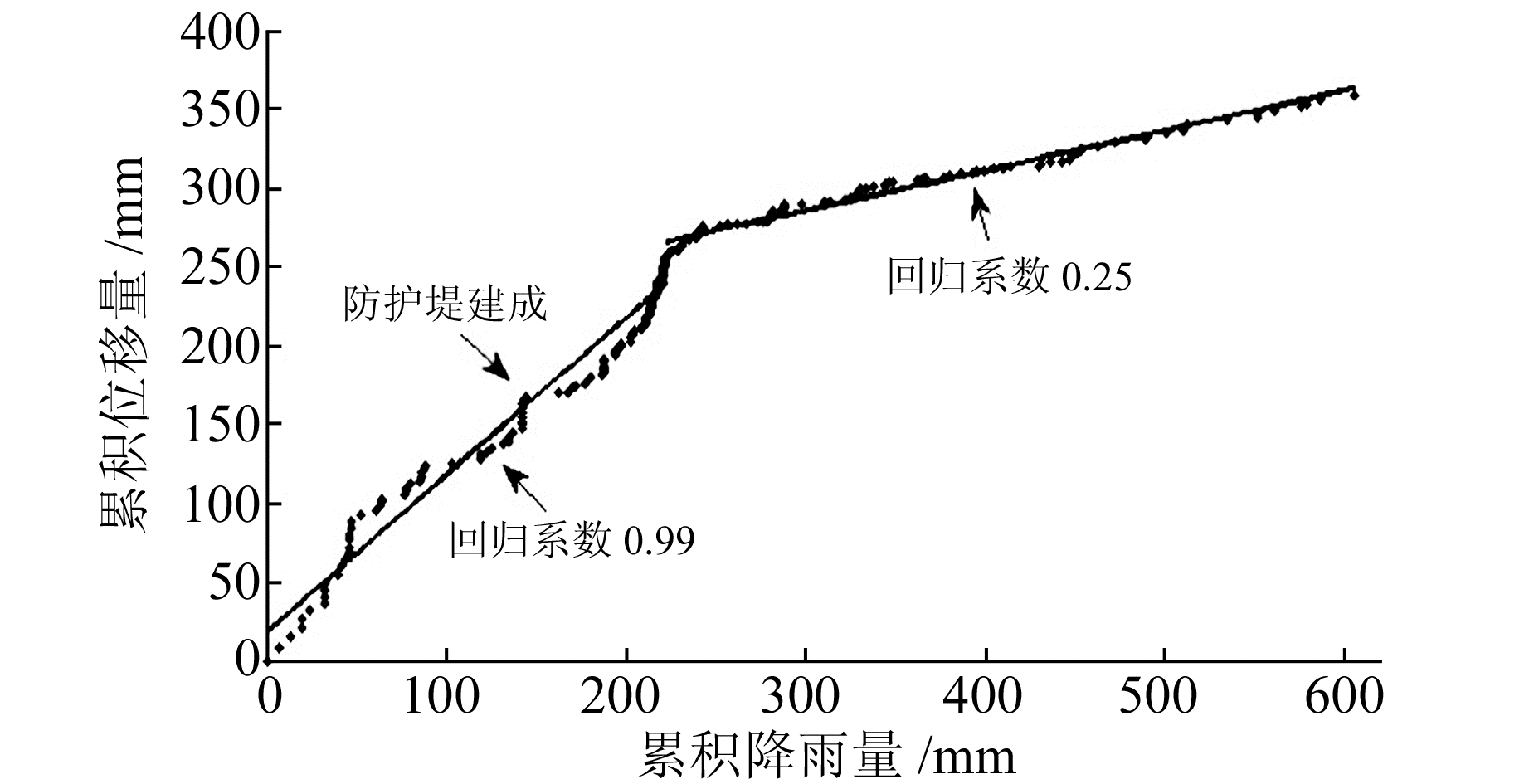
防护墙于2014-06上旬开始施工,同年10月中旬建成。由图 5可知,在防护墙建成约130 d后,易滑坡山体累积位移量与累积降雨量之间的比例关系发生改变,从每降雨1 mm即发生0.99 mm的位移量,降低到每降雨1 mm发生0.25 mm的位移量,推测防护墙对减慢山体位移速率起到一定的积极作用。两个时间段内累积位移量与累积降雨量的相关系数分别为0.984和0.987,这说明该易滑坡山体位移主要受降雨影响,为降雨型滑坡。在边坡监测工作中,可将实时的位移量和降雨量作为滑坡预警的重要依据。
|
图 5 累积降雨量与累积位移量分段线性关系 Fig. 5 Segmental linear relationship of cumulative rainfall and cumulative displacement |
以阻尼LAMBDA算法为基础,结合BDS/GPS单频接收机和GPRS DTU,编写变形监测软件并建立WEB服务器程序,实现一种多设备集成化、分布式、网络化的实时远程GNSS变形监测系统。
以四川理县边坡监测应用为例,对比了GPS、BDS及组合系统下单历元解算效果。BDS无论是在观测卫星数、PDOP值,还是解算效果方面均优于GPS。变形监测系统获取了该边坡长达23个月的位移趋势,该易滑坡山体属于土质边坡,山体位移主要受降雨影响。
| [1] |
唐亚明, 张茂省, 薛强, 等. 滑坡监测预警国内外研究现状及评述[J]. 地质评论, 2012, 58(3): 533-541 (Tang Yaming, Zhang Maosheng, Xue Qiang, et al. Landslide Monitoring and Early-Warning: An Overview[J]. Geological Review, 2012, 58(3): 533-541)
(  0) 0) |
| [2] |
汪亮, 李子申, 袁洪, 等. BDS/GPS/GLONASS组合的双频单历元相对定位性能对比分析[J]. 科学通报, 2015, 60(9): 857-868 (Wang Liang, Li Zishen, Yuan Hong, et al. Validation and Analysis of the Performance of Dual Frequency Single-Epoch BDS/GPS/GLONASS Relative Positioning[J]. Chinese Science Bulletin, 2015, 60(9): 857-868)
(  0) 0) |
| [3] |
Odolinski R, Teunissen P J G, Odijk D. Combined BDS, Galileo, QZSS and GPS Single-Frequency RTK[J]. GPS Solutions, 2015, 19(1): 151-163 DOI:10.1007/s10291-014-0376-6
(  0) 0) |
| [4] |
李征航, 刘万科, 楼益栋, 等. 基于双频GPS数据的单历元定向算法研究[J]. 武汉大学学报:信息科学版, 2007, 32(9): 753-756 (Li Zhenghang, Liu Wanke, Lou Yidong, et al. Heading Determination Algorithm with Single Epoch Dual-Frequency GPS Data[J]. Geomatics and Information Science of Wuhan University, 2007, 32(9): 753-756)
(  0) 0) |
| [5] |
唐卫明, 邓辰龙, 高丽峰. 北斗单历元基线解算算法研究及初步结果[J]. 武汉大学学报:信息科学版, 2013, 38(8): 897-901 (Tang Weiming, Deng Chenlong, Gao Lifeng. Preliminary Results of Single Epoch Baseline Solution Based on Beidou Navigation Satellite System[J]. Geomatics and Information Science of Wuhan University, 2013, 38(8): 897-901)
(  0) 0) |
| [6] |
刘根友, 朱耀仲, 韩保民. GPS单历元定位的阻尼LAMBDA算法[J]. 武汉大学学报:信息科学版, 2004, 29(3): 195-197 (Liu Genyou, Zhu Yaozhong, Han Baomin. Damped LAMBDA Algorithm for Single Epoch GPS Positioning[J]. Geomatics and Information Science of Wuhan University, 2004, 29(3): 195-197)
(  0) 0) |
| [7] |
李鹤峰, 党亚民, 秘金钟, 等. BDS与GPS、GLONASS多模融合导航定位时空统一[J]. 大地测量与地球动力学, 2013, 33(4): 73-78 (Li Hefeng, Dang Yamin, Bei Jinzhong, et al. Research on Spatio Tempora Unification of BDS/GPS/GLONASS Multi-Mode Fusion Navigation and Positioning[J]. Journal of Geodesy and Geodynamics, 2013, 33(4): 73-78)
(  0) 0) |
| [8] |
程鹏飞, 文汉江, 成英燕, 等. 2000国家大地坐标系椭球参数与GRS 80和WGS 84的比较[J]. 测绘学报, 2009, 38(3): 189-194 (Cheng Pengfei, Wen Hanjiang, Cheng Yingyan, et al. Parameter of the CGCS 2000 Ellipsoid and Comparisons with GRS 80 and WGS 84[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(3): 189-194 DOI:10.3321/j.issn:1001-1595.2009.03.001)
(  0) 0) |
| [9] |
楼益栋, 龚晓鹏, 辜声峰, 等. GPS/BDS混合差分RTK定位方法及结构分析[J]. 大地测量与地球动力学, 2016, 36(1): 1-5 (Lou Yidong, Gong Xiaopeng, Gu Shengfeng, et al. An Algorithm and Results Analysis for GPS+BDS Inter-System Mix Double-Difference RTK[J]. Journal of Geodesy and Geodynamics, 2016, 36(1): 1-5)
(  0) 0) |
| [10] |
湛雷冲, 邹彤. 基于WebSocket的地震记录仪远程监控系统[J]. 大地测量与地球动力学, 2016, 36(3): 101-105 (Zhan Leichong, Zou Tong. Remote Monitoring System for Seismic Records Based on WebSocket[J]. Journal of Geodesy and Geodynamics, 2016, 36(3): 101-105)
(  0) 0) |
2. University of Chinese Academy of Sciences, A19 Yuquan Road, Beijing 100049, China;
3. China Earthquake Networks Center, 5 Nanheng Street, Sanlihe, Beijing 100045, China;
4. Key Laboratory of Earthquake Geodesy, Institute of Seismology, CEA, 40 Hongshance Road, Wuhan 430071, China
 2017, Vol. 37
2017, Vol. 37



