自弹性回跳理论提出以来,大量震例表明地震的孕育和发生与断层运动存在密切关系,随后位错理论的出现为断层运动研究提供了理论基础,包括描述同震形变的位错理论、描述震间形变的负位错理论、震后形变理论。有关断层运动的深入研究对于提高强震孕育过程的认识水平意义重大,对提高断层强震危险性评价的科学性具有指导意义。近30 a来,随着空间大地测量技术的飞速发展,人类逐渐能够获取全天候、高精度、连续覆盖的三维地表形变信息,而以GPS和InSAR技术为代表的空间观测手段越来越多地应用于地震形变研究[1],尤其是地震大地测量学概念的提出[2],逐渐累积了大量关于地壳运动和断层运动的实例,为进一步认识地震孕育、发生机理提供了丰富的资料基础。因此,在地震形变资料极为丰富的今天,梳理基于地震大地测量观测技术研究断层运动的发展历史和研究现状,对于正确认识地震孕育、发生机理,研究大陆构造的现今变形过程都具有重要的意义。
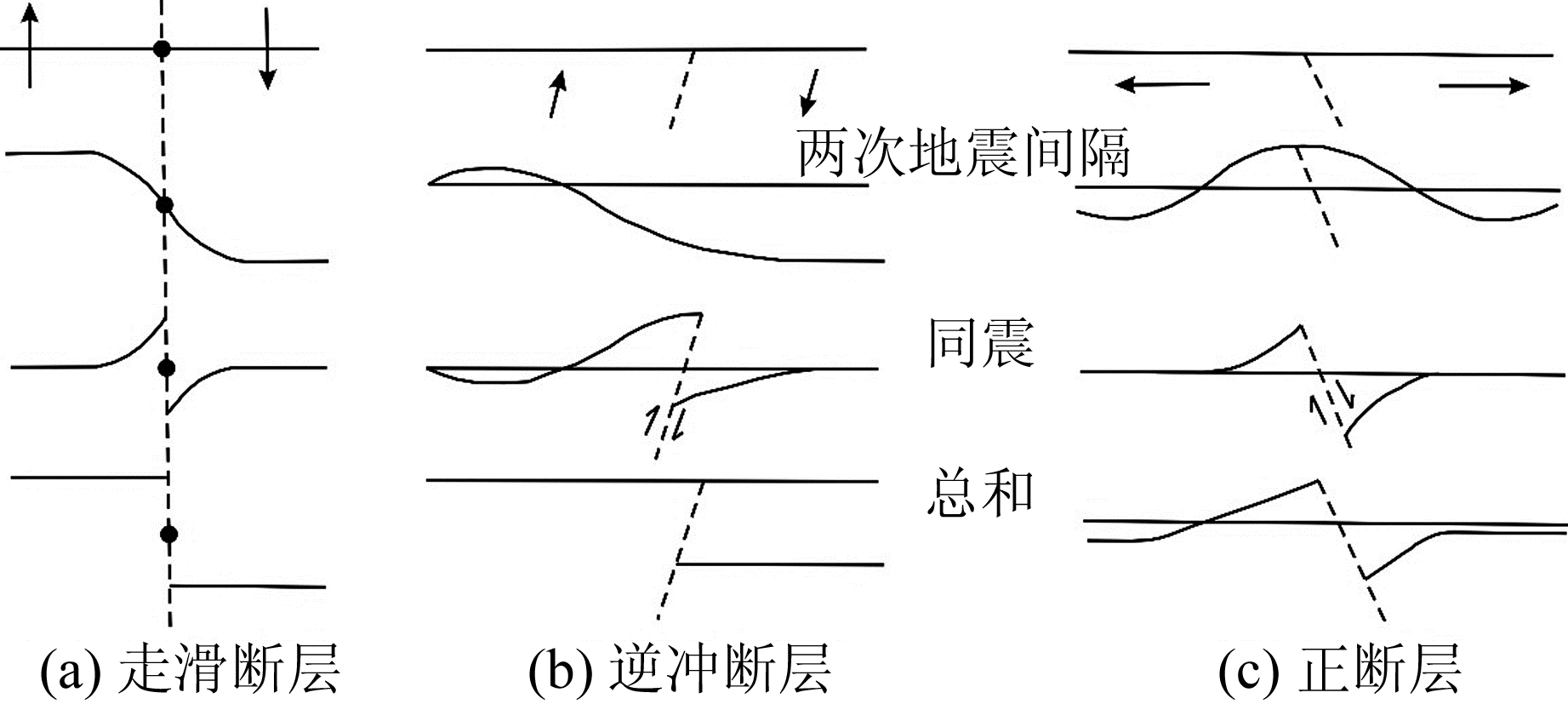
1 断层位错模型的发展 1.1 弹性回跳理论1906年美国加州旧金山发生8.2级地震,震后4 a,Reid[3]根据震前和同震大地测量观测资料,提出弹性回跳理论用以解释浅源地震的力学机制。该理论是世界上最早试图解释地震孕育、发生过程的理论,也是迄今为止应用最广的地震成因假说,其直观地描述了孕震区发震断层附近的地壳形变过程:地震发生前断层两侧块体存在相对运动,使得断层附近产生弹性应变能积累,当应变积累到断层所能承受的强度后断层即发生错动,引发地震。弹性回跳理论指出了地震孕育过程、断层运动与地壳形变之间的密切联系,其要点包含3个方面[4]:1)地震是由断层运动引起的;2)断层运动导致其两侧岩石发生变形并积累能量,岩石破裂时能量随之释放;3)断层带各处能量积累不同步。其中,第一个方面使后续的大量地震研究集中于地震断层;而第二和第三方面阐明了地震的能量来源及震前、震后和同震的地壳形变状态,为利用形变数据确定发震地点提供了理论支撑。断层分为走滑断层、正断层和逆断层,对于走滑断层,Reid[3]给出了较为详细的描述;对于逆冲断层,Fitch等[5]以日本西南地震为例分析了俯冲带上逆冲地震的弹性回跳模型;对于正断层,Koseluk和Rundle等[6-7]讨论了加拿大两处正断层地震震前、震后的弹性回跳模型,并用粘弹性数值模拟技术模拟了形变场的空间分布,总结了3类地震断层在地震周期各个阶段(震间、同震、震后)的形变场特征(图 1)。震间期断层两侧存在差异运动,近场小、远场大;同震时,近断层处反向运动,即回跳,其中走滑断层展示了平面方向的运动,逆冲断层和正断层展示了剖面方向的运动。
|
图 1 走滑断层、逆冲断层和正断层的弹性回跳模型 Fig. 1 Schematic map of elastic rebound model for strike-slip fault, reverse fault, and normal fault (a)为走滑断层俯视图,箭头表示沿断层迹线(虚线)长期相对 运动,震间与同震变形的总和是一个地震周期产生的总变形; (b)为逆冲断层剖面图,箭头表示断层(虚线)附近的震间位移, 而同震变形产生的运动与应变累积阶段的运动相反,总和表示 同震与震间的总变形;(c)为正断层剖面图,箭头表示震间运动, 震间运动在断层(虚线)附近产生了弯隆,同震位移使断层下盘 上升,上盘下降,总和表示断层相对于原始水平面的总变形 |
弹性回跳理论属于地震断层成因假说,曾经一段时间面临着各种挑战。1966年,Brace等[8]提出粘滑摩擦理论,发展了弹性回跳理论,对于研究慢地震、地震复发周期、解释观测数据都有非常显著的效果。但由于断层摩擦参数的复杂性,使得地震发生规律依然无法精确预测。因此,如何确定摩擦参数,利用摩擦理论来研究地震发生过程,依然还有很长的路要走。
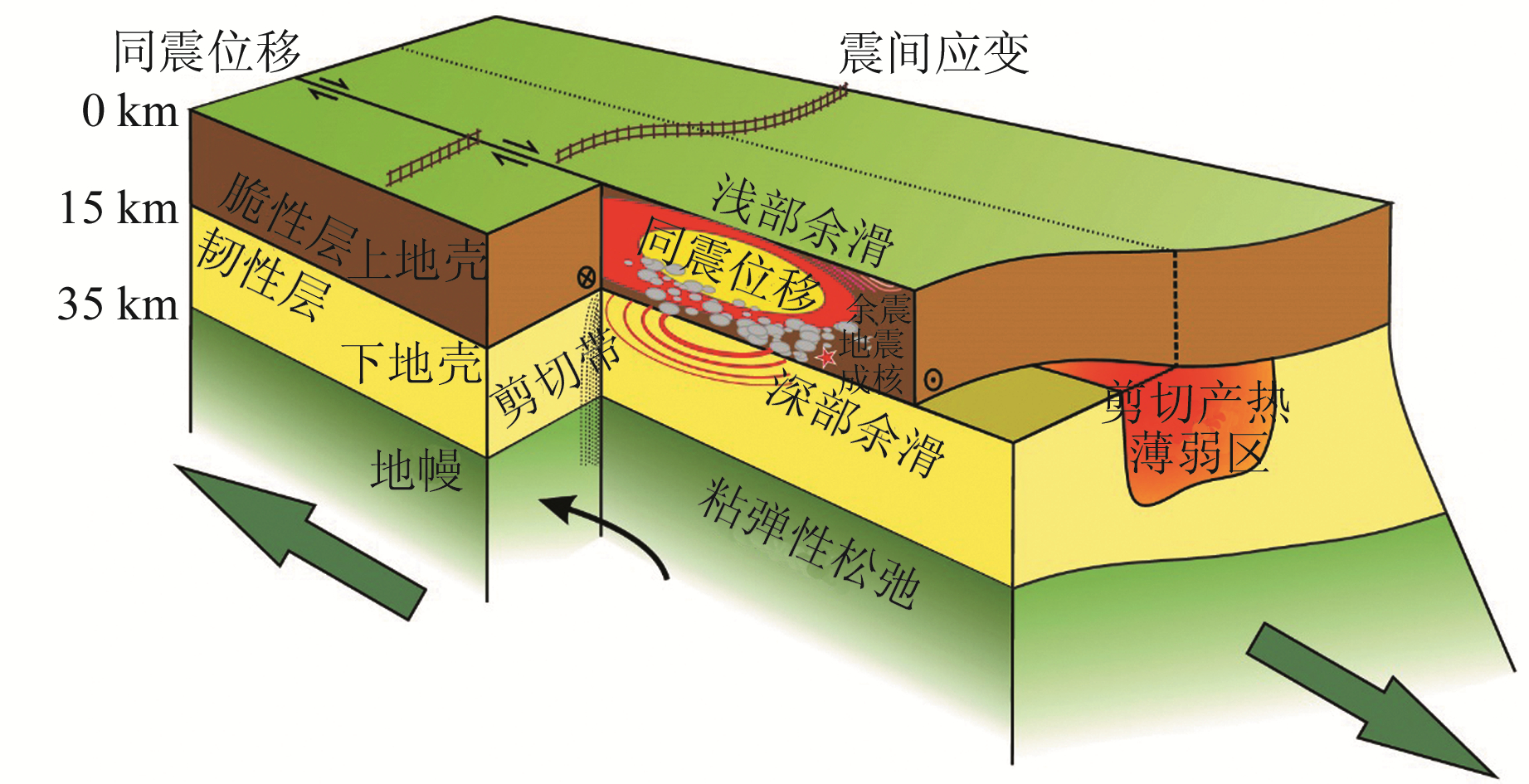
1.2 位错理论地震周期包括震间(地震孕育)、同震(地震发生)和震后(震后效应)3个阶段[9]。目前,基于地震大地测量观测资料可以观测到断层在整个地震周期3个阶段的不同变形(图 2),即两次大地震之间断层两侧应变积累引起的地表变形(震间形变)、孕震时上地壳的同震错动在地表产生的变形(同震形变)、地震发生后发震断层的余滑以及塑性的下地壳和上地幔引起的粘弹性松弛产生的地表变形(震后形变)。
|
图 2 地震周期不同阶段变形过程的概念模型[10] Fig. 2 Schematic model of deformation process for different earthquake cycle phases[10] |
1) 同震形变描述
为了建立地表形变和地震断层之间的数学模型,Steketee[11]把位错理论引入地震学,首先建立均匀介质模型,假设断层面发生错动,即发生不连续位移,进一步导出走滑断层的位移格林函数。之后,国内外诸多学者对弹性半无限空间的同震变形问题开展了大量研究,直到1985年,日本学者Okada[12]整理并总结了前人的工作,给出了一套实用的同震变形计算公式——半无限空间介质内部的同震形变计算方法,该方法可以计算断层运动引起的位移、应变和倾斜变形。目前,Okada的计算公式[12-13]已经成为半无限空间均匀弹性介质地球模型位错理论的经典表达式。
位错理论的进一步发展,是建立远场形变与位错源之间的关系,主要是关于球形地球模型的研究。20世纪60年代后期,Ben-Menahem等[14-15]推导了均质无自重球形地球模型的位移和应变解析解,结果表明对于浅源地震,地球的曲率影响较小,但地球分层以及横向不均匀性可能存在影响。关于球形地球模型位错理论的系统研究,孙文科[16-17]多年来开展了开创性研究,推导了球形对称弹性地球模型位错产生的引力位和重力变化,在世界上首次解决了球形地球模型的同震重力变化问题,之后把该理论推广到了位移和应变的研究。考虑地壳深部韧性介质的影响,Pollitz[18]早期研究了不考虑重力作用下粘弹性地球模型中位错引起的位移和应变,进一步研究了层状地球模型的同震形变和应变,讨论了地球曲率和分层作用的影响,发现地幔的粘滞性对远场震后变形影响较大。
可见,同震位错模型研究已越来越精细,在研究弹性回跳的同震位移方面经历了从二维到三维、从近场到远场、从弹性到粘弹性,从不考虑自重到考虑自重,从均匀半空间到分层半空间的发展过程,目前已经能够非常精确地表述同震位移,然而由于地质构造的复杂性,地球介质属性在横向上也存在极大的差异,需要进一步完善。同时,传统位错理论只考虑了发震断层3个方向的平动,其转动和扭动会产生什么样的位移场,是今后需要进一步研究的问题。
2) 震间形变描述
位错理论描述了弹性回跳过程中同震位移的数学表示,但在孕育地震的长期构造运动中,断层两侧是如何运动的,如何用数学公式进行定量描述?随着位错理论的发展,关于震间断层运动的数学描述也逐渐发展起来。Savage等[19]基于形变观测资料建立了走滑断层的一维震间位错模型,即反正切位错模型(也称螺旋位错模型),该模型假设断层面从地表向地下无限深处延伸,同时将断层面以某一深度分为上下两部分,下部分自由滑动,浅部(脆性上地壳)不能自由滑动,深部断层面自由滑动对浅部断层面产生加载作用,从而产生应变积累,即浅部断层面闭锁。深度分界定义为闭锁深度,与区域孕震层的厚度有关。
反正切位错模型定义了走滑断层滑动速率与闭锁深度之间的关系式,因其简单、实用,虽然已经提出40多年,至今仍然使用广泛,例如应用其对土耳其安纳托利亚断层、我国的阿尔金断裂带和鲜水河断裂带开展的研究,为利用大地测量观测资料估计走滑断层的滑动速率和闭锁深度提供了理论基础。
随后,国内外多名学者对上述经典反正切位错模型进行了改进。Savage等[20]指出弹性块体的螺旋位错模型求得的断层闭锁深度与根据地震观测和断层强度的实验室分析结果不一致,因此建立了下层粘弹性耦合的位错模型来反演断层的闭锁深度,并将该模型用于美国南加州Big Bend地区。Meade等[21]采用经典的上层弹性下层麦克斯维尔粘弹性的三维地壳结构,根据GPS数据反演了南加州地区的应变积累率和地壳的粘滞系数。Savage等认为采用单一伯格矢量描述的位错模型并不能够真实模拟震间的形变机制,提出采用多位错源叠加的模型来确定断层相对真实的闭锁深度和滑动速率,尽管增加了反演的参数和不确定性,但是作为更接近真实的模型,对于位错模型的发展具有重要意义。Jolivet等[22]认为常用的弹性半空间震间形变模型会导致滑动速率和断层闭锁深度的估计偏差,为了克服该问题采用球面薄板剪切模型来确定断层的滑动速率和闭锁深度,与常规位错方法相比,更有利于得到与实际一致的滑动速率。Pollitz等在考虑震间形变时,充分考虑了背景运动、震后松弛、浅层蠕滑、深层蠕滑、重力崩塌、地幔对流的拖曳力对地表位移的影响,利用这种复杂而接近现实的模型来分析美国西部的震间形变。Burgette等采用三维数值方法模拟了Cascadia俯冲区域垂直形变数据,分析了闭锁深度与高程变化率之间的关系。Loveless等根据日本高空间分辨率GPS数据,分析了球面线性板块模型对地表位错量的贡献。Kanda将运动学的弹性位错模型发展为弹性俯冲板块模型,用于对美国西部俯冲边界的研究[17]。
Martsu’ura等[23]提出一种新的基于Okada的刚性块体负位错模型用于分析震间形变,该模型将震间期块体边界深部塑性区的相对运动等价为浅部脆性区断层闭锁部分与刚性块体运动部分的叠加,断层破裂时产生的同震位错量即是负位错量。采用该位错模型,考虑间接先验信息的贝叶斯估计方法重新估算了日本断层的滑动速率和闭锁深度。Fukahata等[24]将螺旋位错模型发展为动力学模型,用于日本西南Shikoku水准数据的反演,并计算了该地区的地震复发周期。Fukahata等[25]将刚性负位错模型发展为弹性/粘弹性位错模型,Martsu’ura等[26]采用考虑直接和间接先验信息的贝叶斯估计负位错模型来反演断层的几何参数和运动速率。McCaffrey等[27]开发了一套负位错反演程序包(TDEFNODE),可以基于大地测量观测资料(GPS、水准、InSAR)反演块体的欧拉极和块体边界断层二维断层面上的滑动亏损和闭锁程度,在全球较大俯冲带地区得到了广泛应用。国内利用负位错模型开展的断层震间形变研究主要集中在应用层面,应用区域包括中国西部主要块体边界断裂、滇西地区主要断裂、海原断裂带、龙门山断裂带等。
3) 震后形变描述
弹性回跳理论中,强震发生之后,断层附近会产生较大的位移,距断层较远的区域运动相对滞后,这种现象有三种可能的物理机制[28],分别是余滑(afterslip)、粘弹性松弛(viscoelastic relaxation)和孔隙弹性松弛(poroelastic relaxation)。余滑机制是指在震后较短时间内,断层由于惯性继续向同震错动方向滑动,可以用位错模型来描述,其作用时间在震后较短的时间内。孔隙弹性松弛模型也称为孔隙弹性回弹(poroelastic rebound)模型,主要指地震产生孔隙水压梯度,震后孔隙水重新分布平衡,从而引起地壳收缩或者扩张。震后粘弹性松弛机制指的是断层同震库仑应力变化引起下地壳和上地幔韧性层的应力发生变化,引起震后地表变形。国际上针对震后粘弹性松弛机制的相关研究较多,其中最具代表性的有:Pollitz开发的VISCO3D软件,用于计算球面上震后粘弹性松弛产生的形变场,该软件对于计算远场地震的影响效果最好;汪荣江开发的PSGRN/PSCMP软件,用于计算分层半空间内地震引起的震后粘弹性松弛效应,该软件由于其高效的计算效率和简洁的使用方式,在国内外应用非常广泛。
一般来说,没有哪一种机制能够解释所有的地震震后形变机理,且大多情况下对于某个地震而言,上述三种机制会同时发生。余滑往往引起局部的形变,而粘弹性松弛效应往往引起较大范围的地表形变。震后余滑和粘弹性松弛主要发生在15~30 km深的下地壳,而孔隙弹性松弛则一般发生在0~15 km深的上地壳。
关于震后形变的应用,目前主要用于分析大地震对后续发生的地震的粘弹性应力触发,但需要建立复杂的地球模型和断层模型,因此,数值模拟技术用于复杂介质模型的震后应力触发也是一种值得考虑的方法。
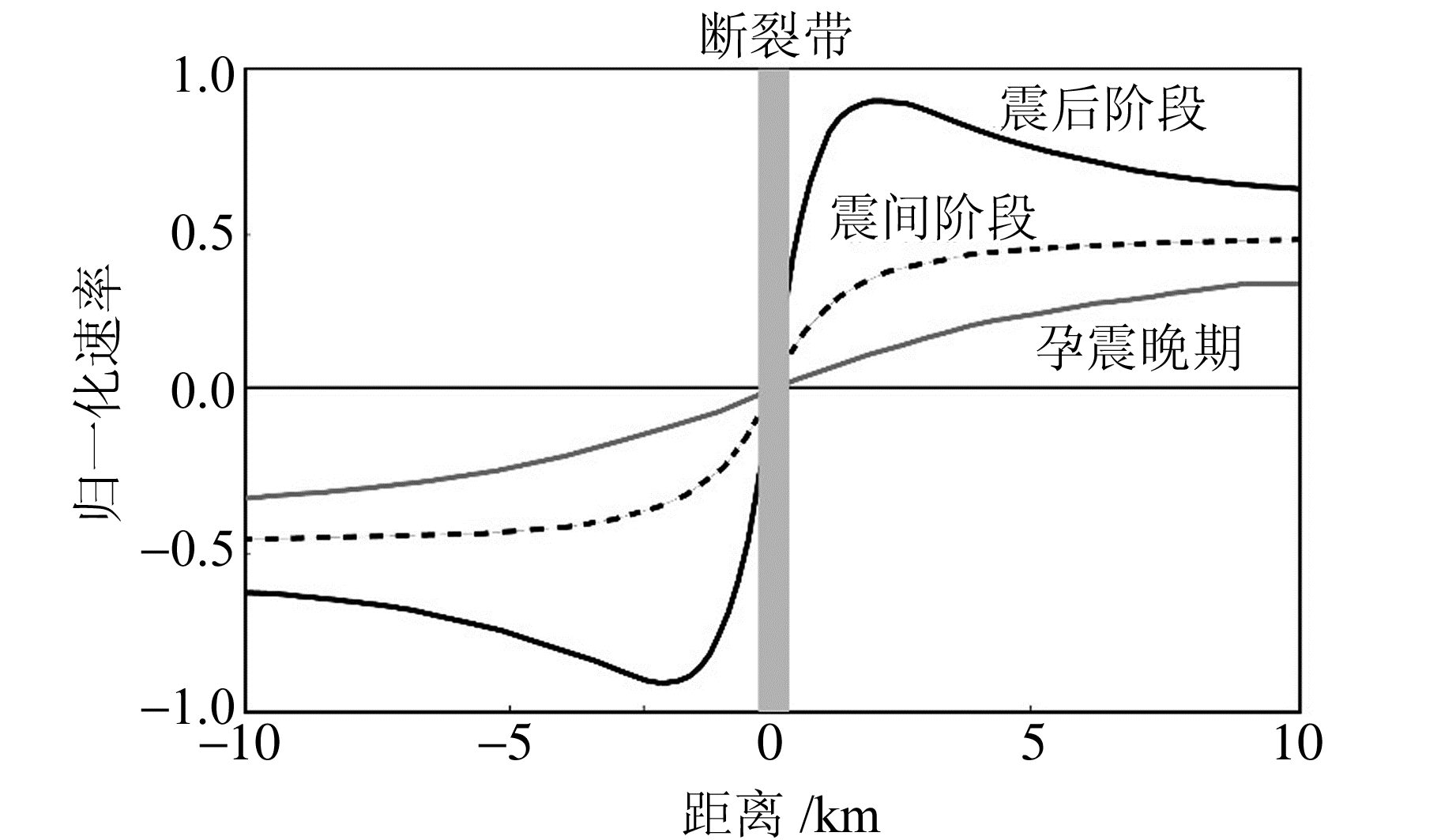
2 基于地震大地测量观测判定断层不同孕震阶段强震震例研究表明,大地测量观测资料在地震不同阶段的分析过程中都是最为重要的约束资料之一,因此研究断层现今孕震状态的一种直接且有效的方式是研究其现今的地壳形变状态[1]。从力学机理角度分析,断层活动与地壳形变以及强震孕育过程之间存在着密切关系,即与断层活动有关的地壳形变状态在强震轮回的不同阶段具有不同的表现形式[21, 29](图 3)。同时,震间不同孕震阶段断层两侧的水平地壳变形态势也存在一定差异,即最近一次地震的离逝时间越长,断层两侧形变观测的曲线形态越平缓,此时断层的滑动速率越小、闭锁深度越深,发生地震的概率也就越高[30]。因此通过分析研究断层两侧的水平变形态势,以及反演获得的滑动速率和闭锁深度,可以判断断层所处的孕震阶段。近些年来,与强震孕育阶段(震间)断层活动引起的地壳形变特征及其机理分析有关的研究在逐年增多,如有学者基于反正切位错理论、Okada位错模型、负位错理论模型和Smith-3D体力模型等在天山构造带、鲜水河断裂带、海原断裂带、阿尔金断裂带、东昆仑断裂带、土耳其安纳托利亚断裂等很多大型断裂构造上开展断层闭锁深度和滑动速率的反演,并结合相关断层地质滑动速率和强震活动时序特征给出断层位移亏损,进而判断断层可能处于的孕震阶段。
|
图 3 走滑断层不同孕震阶段变形特征的理论模式 Fig. 3 Theoretical model of different earthquake cycle phases for strike slip fault |
随着GPS观测站密度的增加和InSAR数据的应用,结合断层面凹凸体理论和速率-状态摩擦本构定律,学者们逐渐认识到震间阶段的断层在不同深度的滑动亏损程度和闭锁程度存在差异。Shirzaei等[31]利用InSAR和蠕变仪形变观测资料共同约束,反演获取了美国加州Hayward断层的震间滑动分布,并结合背景地震分布信息圈定断层面上的无震滑移部位和潜在的孕震凹凸体部位,估计未来可能发生强震的断层段落;Jolivet等[32]以GPS和InSAR观测资料得到的区域长期平均地壳形变速率为约束,反演获得美国加州圣安德烈斯断层中段的震间断层面滑动分布,并结合历史地震破裂分布结果,给出断层面可能处于强烈闭锁状态的段落,为地震危险性评估提供重要依据。Jiang等[33]基于GPS和InSAR结果,反演了鲜水河-安宁河-则木河断裂带断层面上的闭锁程度,圈定了断层面潜在的孕震凹凸体,给出了分段地震危险性。赵静等[34]采用TDEFNODE负位错模拟软件计算了中国西部主要块体边界断裂的闭锁状态和滑动速率,给出断层不同段落的现今地震危险程度。可见,具有高空间分辨率的GPS和InSAR地壳形变场的出现,使得利用地震大地测量观测资料判定强震孕育阶段(震间)断层不同段落的活动状态成为可能。
3 结语从地震预测的角度分析,断层运动的研究对于地震危险性分析及强震危险地点的判定具有重要意义。地壳形变是断层运动的直接表现形式之一,因此应用地震大地测量观测资料研究断层运动进行地震预测预报,是最直接、最有效的手段之一。弹性回跳理论作为从大地测量技术发展而来的研究地震发生机理最早的理论,回顾其100余年的发展历史可以发现,随着新技术、新理论的涌现,弹性回跳理论也在逐渐完善。位错理论的出现最初是描述弹性回跳过程中同震位移的数学表示,随着地震大地测量技术的进步,尤其是高时空分辨率的空间大地测量技术(例如GPS、InSAR)的发展,使得利用位错模型描述断层在不同地震周期阶段(同震、震间、震后)的运动方式和变形模式方面取得了重要进展,对于进一步探究地震发生机理具有重要的指导意义。在地震预测应用方面,随着地震大地测量观测资料时空分辨率的日益提高以及位错模型的日臻完善,基于地震大地测量观测资料和位错理论研究判定断层可能处于的孕震阶段,是需要重点关注的领域之一。
随着地震台网空间分辨率的逐渐提高,通过数字地震学方法能够精确识别断层面上分布的潜在孕震凹凸体,为判定强震可能发生的断层段落提供了重要的依据。目前,随着高时空分辨率地表形变场的获取、大地测量反演技术的发展,以及地震大地测量观测技术的日新月异,使得利用大地测量观测资料约束获取断层面孕震凹凸体的分布逐渐成为可能。未来,针对潜在重点地震危险区,联合数字地震学和大地测量学观测结果,识别和圈定断层面可能存在的孕震凹凸体分布,是地震大地测量学的一个重要发展方向。
| [1] |
张培震, 邓起东, 张国民, 等. 中国大陆的强震活动与活动地块[J]. 中国科学:地球科学, 2003, 33(增1): 12-20 (Zhang Peizhen, Deng Qidong, Zhang Guomin, et al. Active Tectonic Blocks and Strong Earthquakes in the Continent of China[J]. Science China Earth Sciences, 2003, 33(S1): 12-20)
(  0) 0) |
| [2] |
周硕愚, 吴云, 姚运生, 等. 地震大地测量学研究[J]. 大地测量与地球动力学, 2008, 28(6): 77-82 (Zhou Shuoyu, Wu Yun, Yao Yunsheng, et al. Research of Earthquake Geodesy[J]. Journal of Geodesy and Geodynamics, 2008, 28(6): 77-82)
(  0) 0) |
| [3] |
Reid H F. The Mechanics of the Earthquake, the California Earthquake of April 18, 1906[R]. The State Earthquake Investigation Commission, Washington D C, 1910
(  0) 0) |
| [4] |
刘力强. 弹性回跳模型:从经典走向未来[J]. 地震地质, 2014, 36(3): 825-832 (Liu Liqiang. Elastic Rebound Model: From the Classic to the Future[J]. Seismology and Geology, 2014, 36(3): 825-832 DOI:10.3969/j.issn.0253-4967.2014.03.021)
(  0) 0) |
| [5] |
Fitch T J, Scholz C H. Mechanism of Underthrusting in Southwest Japan: A Model of Convergent Plate Interactions[J]. Journal of Geophysical Research:Solid Earth, 1971, 76(29): 7260-7292 DOI:10.1029/JB076i029p07260
(  0) 0) |
| [6] |
Koseluk R A, Bischke R E. An Elastic Rebound Model for Normal Fault Earthquakes[J]. Journal of Geophysical Research, 1981, 86(B2): 1081-1090 DOI:10.1029/JB086iB02p01081
(  0) 0) |
| [7] |
Rundle J B. Models of Crustal Deformation[J]. Review of Geophysics, 1983, 21(6): 1454-1458 DOI:10.1029/RG021i006p01454
(  0) 0) |
| [8] |
Brace W F, Byerlee J D. Stick-Slip as a Mechanism for Earthquakes[J]. Science, 1966, 153(3739): 990-992 DOI:10.1126/science.153.3739.990
(  0) 0) |
| [9] |
Scholz C H. Earthquakes and Friction Laws[J]. Nature, 1998, 391(1): 37-42
(  0) 0) |
| [10] |
Elliott J R, Walters R J, Wright T J. The Role of Space-Based Observation in Understanding and Responding to Active Tectonics and Earthquakes[J]. Nature Communications, 2016, 7
(  0) 0) |
| [11] |
Steketee J A. On Volterra's Dislocations in a Semi-Infinite Elastic Medium[J]. Can J Phys, 1958, 36(2): 192-205 DOI:10.1139/p58-024
(  0) 0) |
| [12] |
Okada Y. Internal Deformation Due to Shear and Tensile Faults in a Half-Space[J]. Bull Seismol Soc Am, 1992, 82(2): 1018-1040
(  0) 0) |
| [13] |
Okada Y. Surface Deformation Due to Shear and Tensile Faults in a Half-Space[J]. Bull Seism Soc Am, 1985, 75(4): 1135-1154
(  0) 0) |
| [14] |
Ben-Menahem A, Singh S J. Eigenvector Expansions of Green's Dyads with Applications to Geophysical Theory[J]. Geophys J Int, 1968, 16(4): 417-452 DOI:10.1111/gji.1968.16.issue-4
(  0) 0) |
| [15] |
Ben-Menahem A, Israel M. Effects of Major Seismic Events on the Rotation of the Earth[J]. Geophys J Int, 1970, 19(4): 367-393 DOI:10.1111/gji.1970.19.issue-4
(  0) 0) |
| [16] |
孙文科. 地震火山活动产生重力变化的理论与观测研究的进展及现状[J]. 大地测量与地球动力学, 2008, 28(4): 44-53 (Sun Wenke. Progress and Current Situation of Research on Theory and Observation of Gravity Change Caused by Seismicity and Volcanism[J]. Journal of Geodesy and Geodynamics, 2008, 28(4): 44-53)
(  0) 0) |
| [17] |
孙文科. 地震位错理论[M]. 北京: 科学出版社, 2012 (Sun Wenke. Earthquake Dislocation Theory[M]. Beijing: Science Press, 2012)
(  0) 0) |
| [18] |
Pollitz F F. Postseismic Relaxation Theory on the Spherical Earth[J]. Bull Seismol Soc Am, 1992, 82(1): 422-453
(  0) 0) |
| [19] |
Savage J C, Burford R O. Geodetic Determination of Relative Plate Motion in Central California[J]. Journal of Geophysical Research, 1973, 78(5): 832-845 DOI:10.1029/JB078i005p00832
(  0) 0) |
| [20] |
Savage J C, Lisowski M. Viscoelastic Coupling Model of the San Andreas Fault along the Big Bend, Southern California[J]. Journal of Geophysical Research:Solid Earth, 1998, 103(B4): 7281-7292 DOI:10.1029/98JB00148
(  0) 0) |
| [21] |
Meade B J, Hager B H. Block Models of Crustal Motion in Southern California Constrained by GPS Measurements[J]. Journal of Geophysical Research:Solid Earth, 2005, 110(B3): 353-353
(  0) 0) |
| [22] |
Jolivet R, Cattin R, Chamot-Rooke N, et al. Thin-Plate Modeling of Interseismic Deformation and Asymmetry across the Altyn Tagh Fault Zone[J]. Geophysical Research Letters, 2008, 35(2): 423-432
(  0) 0) |
| [23] |
Matsu'ura M, Jackson D D, Cheng A. Dislocation Model for Aseismic Crustal Deformation at Hollister, California[J]. Journal of Geophysical Research:Solid Earth, 1986, 91(B12): 12661-12674 DOI:10.1029/JB091iB12p12661
(  0) 0) |
| [24] |
Fukahata Y, Nishitani A, Matsu'ura M. Geodetic Data Inversion Using ABIC to Estimate Slip History during One Earthquake Cycle with Viscoelastic Slip-Response Functions[J]. Geophysical Journal International, 2004, 156(1): 140-153 DOI:10.1111/gji.2004.156.issue-1
(  0) 0) |
| [25] |
Fukahata Y, Matsu'ura M. General Expressions for Internal Deformation Fields Due to a Dislocation Source in a Multilayered Elastic Half-Space[J]. Geophysical Journal International, 2005, 161(2): 507-521 DOI:10.1111/gji.2005.161.issue-2
(  0) 0) |
| [26] |
Matsu'ura M, Noda A, Fukahata Y. Geodetic Data Inversion Based on Bayesian Formulation with Direct and Indirect Prior Information[J]. Geophysical Journal International, 2007, 171(3): 1342-1351 DOI:10.1111/j.1365-246X.2007.03578.x
(  0) 0) |
| [27] |
Mccaffrey R, Qamar A I, King R W, et al. Fault Locking, Block Rotation and Crustal Deformation in the Pacific Northwest[J]. Geophysical Journal International, 2007, 169(3): 1315-1340 DOI:10.1111/gji.2007.169.issue-3
(  0) 0) |
| [28] |
谭凯, 王琪, 王晓强, 等. 震后形变的解析模型和时空分布特征[J]. 大地测量与地球动力学, 2005, 25(4): 23-26 (Tan Kai, Wang Qi, Wang Xiaoqiang, et al. Analytic Models and Space Time Distribution of Postseismic Deformation[J]. Journal of Geodesy and Geodynamics, 2005, 25(4): 23-26)
(  0) 0) |
| [29] |
Savage J C, Prescott W H. Asthenosphere Readjustment and the Earthquake Cycle[J]. Journal of Geophysical Research, 1978, 83(B7): 3369-3376 DOI:10.1029/JB083iB07p03369
(  0) 0) |
| [30] |
Segall P. Earthquake and Volcano Deformation[M]. Princeton: Princeton University Press, 2010
(  0) 0) |
| [31] |
Shirzaei M, Bürgmann R, Taira T. Implications of Recent Asperity Failures and Aseismic Creep for Time-Dependent Earthquake Hazard on the Hayward Fault[J]. Earth and Planetary Science Letters, 2013, 371-372: 59-66 DOI:10.1016/j.epsl.2013.04.024
(  0) 0) |
| [32] |
Jolivet R, Simons M, Agram P S, et al. Aseismic Slip and Seismogenic Coupling along the Central San Andreas Fault[J]. Geophysical Research Letter, 2015, 42(2): 297-306 DOI:10.1002/2014GL062222
(  0) 0) |
| [33] |
Jiang G Y, Xu X W, Chen G H, et al. Geodetic Imaging of Potential Seismogenic Asperities on the Xianshuihe-Anninghe-Zemuhe Fault System, Southwest China, with a New 3-D Viscoelastic Interseismic Coupling Model[J]. J Geophys Res:Solid Earth, 120(3): 1855-1873 DOI:10.1002/2014JB011492
(  0) 0) |
| [34] |
赵静, 江在森, 牛安福, 等. 川滇菱形块体东边界断层闭锁程度与滑动亏损动态特征研究[J]. 地球物理学报, 2015, 58(3): 872-885 (Zhao Jing, Jiang Zaisen, Niu Anfu, et al. Study on Dynamic Characteristics of Locking and Fault Slip Deficit in the Eastern Boundary of the Sichuan-Yunnan Rhombic Block[J]. Chinese J Geophys, 2015, 58(3): 872-885)
(  0) 0) |
 2017, Vol. 37
2017, Vol. 37

