2. 中国空气动力研究与发展中心高速所,绵阳市二环路南段6号,621000;
3. 65185部队,铁岭市,112611
在磁力勘探中,磁测资料处理解释(如磁异常化极、正演和反演等)过程需要已知磁性体的磁化方向。然而,在实际测量中,磁性体除受到感应磁化作用外,还受到剩余磁化的影响。因此,在剩余磁化和感应磁化的影响下,磁性体总磁化方向会产生明显改变,从而影响磁测数据的解释精度[1]。
国内外学者提出了很多估计磁性体磁化方向的方法。Medeiros等[2]提出等效源磁矩反演法估计异常源磁化方向;甘西[3]通过磁场的垂直分量确定水平地形、均匀磁化条件下的磁性体磁化方向;Phillips[4]通过Helbig积分法的直接和间接算法对磁性体磁化方向进行计算;Dannemiller等[5]在2D互相关方法基础上,通过求解化极异常与总梯度模量异常互相关系数确定磁化方向;Gerovska等[6]提出基于磁总场模量异常和磁异常化极数据互相关估计方法;石磊等[7]利用偶极源互相关方法对磁异常的磁化方向进行估计。上述方法对估计磁异常的磁化方向提供了较好的思路,但也存在一些问题,如磁总场模量异常虽然弱敏感于磁化方向,但仍会受到斜磁化的影响产生偏移,抗噪声或抗干扰能力较弱等。
针对上述问题,本文基于三维相关成像的相关理论[8-10],提出基于归一化磁源强度数据与磁总场异常化极数据的磁化方向相关估计方法。首先,以等间隔步长选择一系列的磁化方向数值;然后,对实测磁总场异常数据在不同的磁化方向下进行化极处理;最后,求出磁总场化极数据与实测归一化磁源强度数据的互相关系数,将最大值对应的磁化方向作为最终结果。仿真和实验证明了本文方法的有效性。
1 方法原理 1.1 归一化磁源强度数据磁梯度张量可以由一个二阶矩阵表示为:
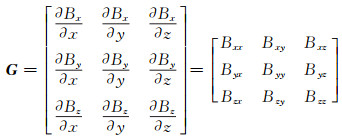
|
(1) |
式中,G为磁梯度张量;Bi(i=x, y, z)为磁场三分量;Bαβ(α, β=x, y, z)为磁梯度张量的9个分量。
归一化磁源强度是由磁偶极子磁梯度张量矩阵推导得到的旋转不变量,其分布位于场源中心。假定磁偶极子在观测面(x, y, z)上引起的磁梯度张量矩阵的特征值按单调递减顺序为λ1≥λ2≥λ3,则归一化磁源强度u (x, y, z)可以表示为[11]:
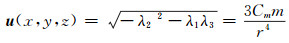
|
(2) |
式中,Cm=10-7 H/m;m为磁偶极子磁矩;r为异常源到观测点的距离。由式(2)可以看出,归一化磁源强度与距离的4次方成反比,与磁矩成正比。
定义一个强剩磁条件下的长方体模型。长方体尺寸为0.6 m×0.6 m×0.2m,定义磁化强度为20 A/m,地磁场倾角为90°,地磁场偏角为0°,实际磁化倾角为50°,磁化偏角为-40°,具体位置如图 1所示,其中白色实线为长方体理论位置。从图 1(a)可以看出,当存在剩余磁化时,磁异常形态复杂,与异常源位置无明显的对应关系;从图 1(b)可以看出,磁总场模量异常极大值位置大致与场源的水平位置相一致,沿异常源的东南方向有一定的偏移;从图 1(c)可以看出,归一化磁源强度正极值与异常源的实际位置具有良好的对应关系,从理论上证明了归一化磁源强度相比磁总场模量更加弱敏感于磁性体磁化方向。

|
图 1 强剩磁条件下的理论磁总场异常、磁总场模量异常和归一化磁源强度异常 Fig. 1 The theoretical total magnetic field anomaly by remanent magnetization, total magnitude data, the normalized source strength data |
利用磁异常化极消除斜磁化对磁异常的影响,将磁总场异常转换为垂直磁化条件下的磁异常。当铁磁物质存在剩余磁化时,磁测异常化极转换需要已知当地背景磁化方向(I0, D0)和铁磁物质的实际磁化方向(I, D)。磁异常化极在频率域内的转换因子为[12]:
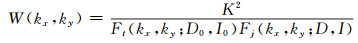
|
(3) |
式中,
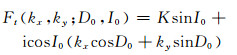
|
(4) |

|
(5) |
式中,kx、ky分别为沿x和y方向的圆频率,K=(kx2+ky2)1/2。
基于这种性质,在磁化方向未知的情况下,将铁磁性体的磁化倾角和磁化偏角等间隔选取一系列的数据点,然后组成磁化方向暂定值。利用这一系列的磁化方向下的化极异常值与归一化磁源强度进行试错,得到不同的互相关系数值。
定义实测区域内的磁异常的化极结果△Trtp与归一化磁源强度数值Tnss的互相关系数C为:
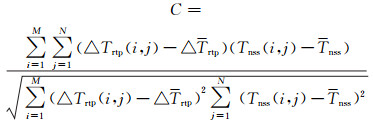
|
(6) |
式中,(M, N)为沿x、y轴的网格划分点数;△Trtp为磁异常化极数据的平均值;Tnss为归一化磁源强度数据的平均值。
根据式(6)计算不同磁化方向下的磁异常化极与归一化磁源强度的互相关系数。获得的C值越大,说明所选的磁化方向越接近真实值。把互相关系数最大值对应的磁化方向作为最终的估计结果。
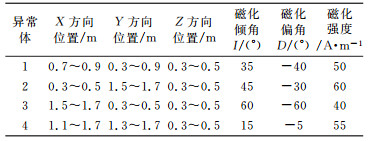
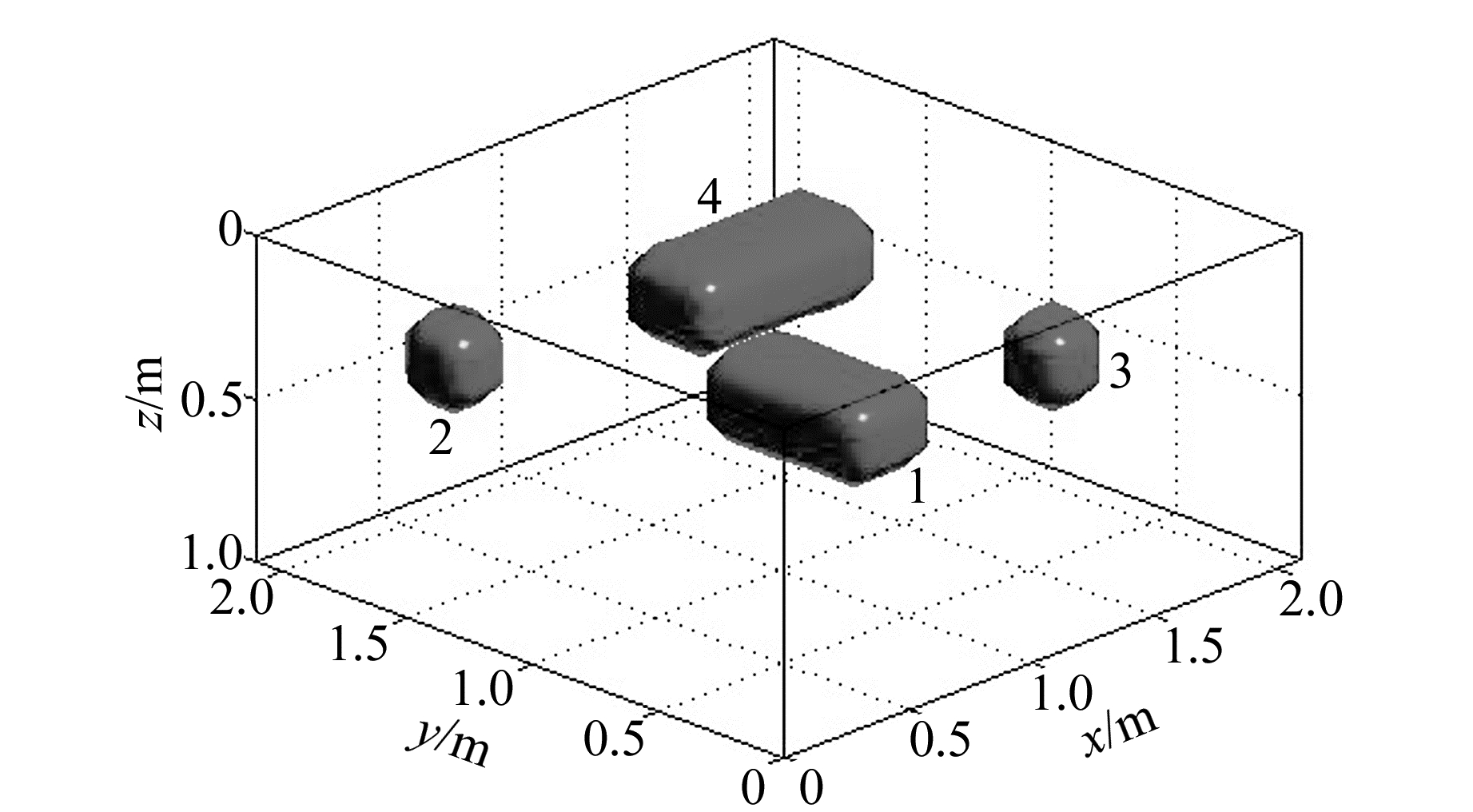
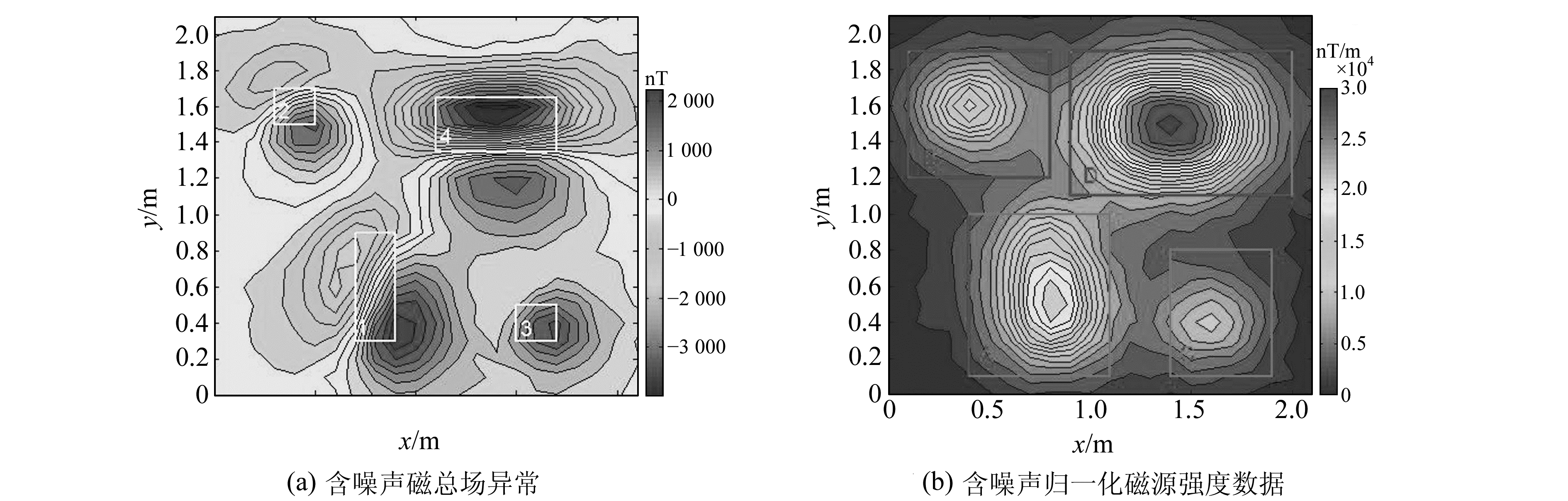
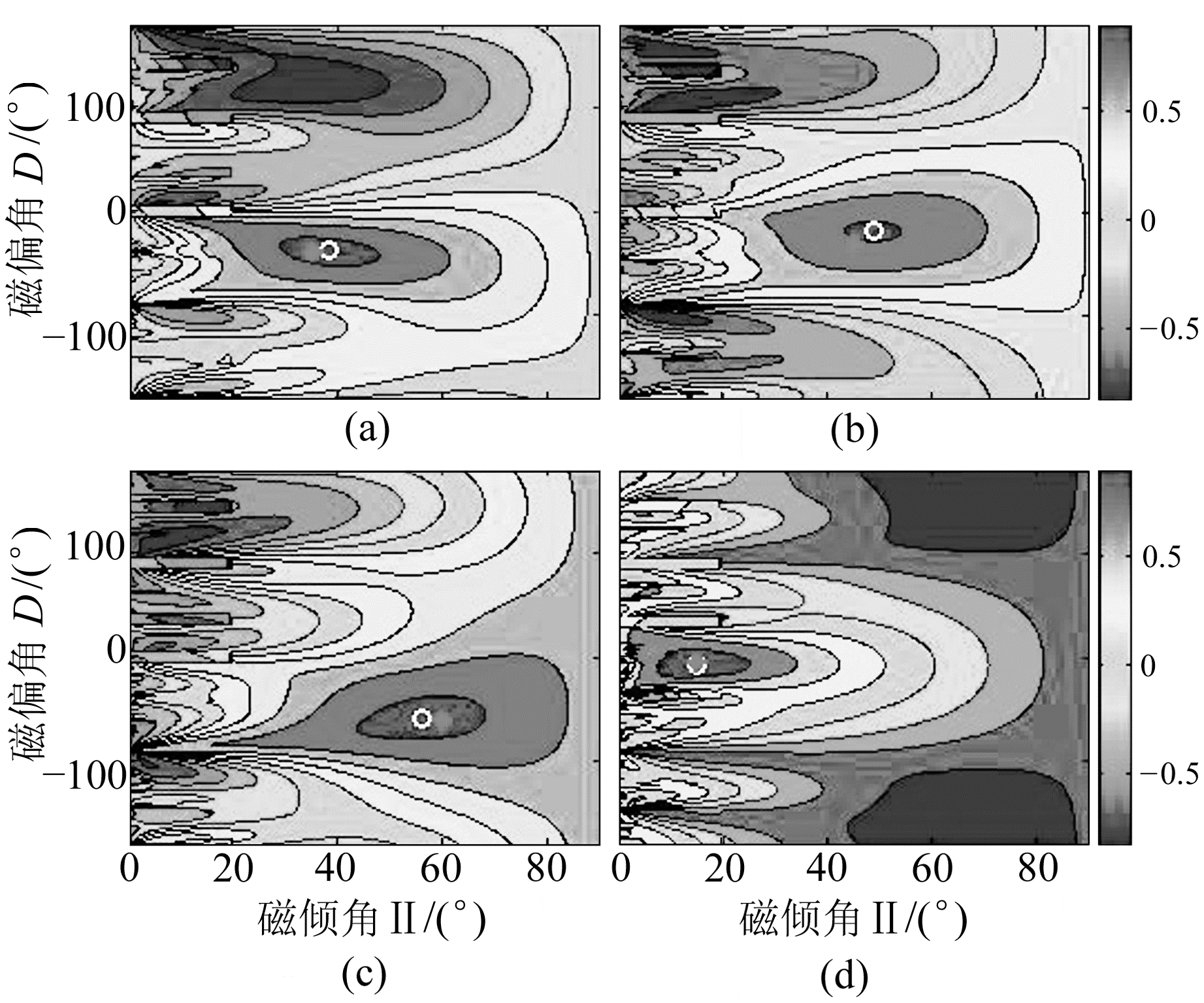
2 仿真分析为验证本文方法的有效性,设计包含4个长方体的组合模型进行测试。将地面的观测点划分为22×22=484个测点网格,每个测点间距为0.1 m,地磁场倾角为60°,地磁场偏角为-20°。测试模型为如图 2所示的组合模型,红色部分表示待测异常体。各部分参数如表 1所示,数字1、2、3和4分别对应不同的异常体模型。对该模型在高度为0的水平观测面上的理论归一化磁源强度数据和磁总场异常数据进行正演计算,并引入基准值5%的高斯随机噪声,获得的磁总场异常及归一化磁源强度数值如图 3所示。其中图 3(a)的白色方框1、2、3、4为各个长方体的实际水平分布,图 3(b)的红色方框为分块区域, 每一个分块区域包含一个孤立的磁异常。取倾角I的范围为0°~90°,步长为1°;偏角D的范围为-180°~180°,步长为1°。将A、B、C、D这4个分块区域内的磁总场异常数据和归一化磁源强度数据作为观测数据,利用式(6)分别计算在不同磁化方向下的磁总场异常化极数据与归一化磁源强度数据的互相关系数。图 4为不同测区的互相关系数云图。每个分块区域内互相关系数最大值对应的磁化方向为最终估计结果。为了进一步对比本方法的有效性,本文利用Gerovska互相关法对上述理论模型进行磁化方向估计实验,得到的总磁化方向结果如表 2所示。本文方法的磁化倾角的估计结果与理论结果相差4°以内,磁化偏角相差12°以内。而Gerovska互相关法估计得到的磁化倾角与理论值最大相差19°,磁化偏角最大相差24°。从表 2结果可以看出,利用归一化磁源强度对磁源进行磁化方向估计所得的结果比Gerovska互相关法所得到的估计结果更加准确。在分块A、B、D中,对比Gerovska互相关法,本文方法估算的结果更加接近实际的磁化方向。由于分块B和A、D的异常叠加较多,导致分块B估计出的磁化方向误差较其他3个分块的误差大,其中磁化偏角与真实值相差12°,而Gerovska互相关法估计的磁化方向值与真实值偏差更大,对于叠加异常的敏感性更高。由此可见,本文方法能够显著提高对近等轴状异常源磁化方向的估计精度,在剩磁条件下能很好地估计异常源的磁化方向。
|
图 2 长方体组合模型 Fig. 2 Prism composition model |
|
|
表 1 理论模型各长方体几何参数和磁化方向 Tab. 1 The geometric parameters and magnetization direction of each prism in synthetic model |
|
图 3 理论模型的含噪声磁总场异常和含噪声归一化磁源强度数据 Fig. 3 The noisy magnetic total field anomalies of synthetic model and normalized magnetic source data |
|
图 4 不同测区的互相关系数 Fig. 4 Cross-correlation coefficient map of different survey areas |
|
|
表 2 利用归一化磁源与化极互相关法和Gerovska互相关法估算总磁化方向 Tab. 2 The estimated magnetization directions by the method by using normalized source strength and Gerovska's method |
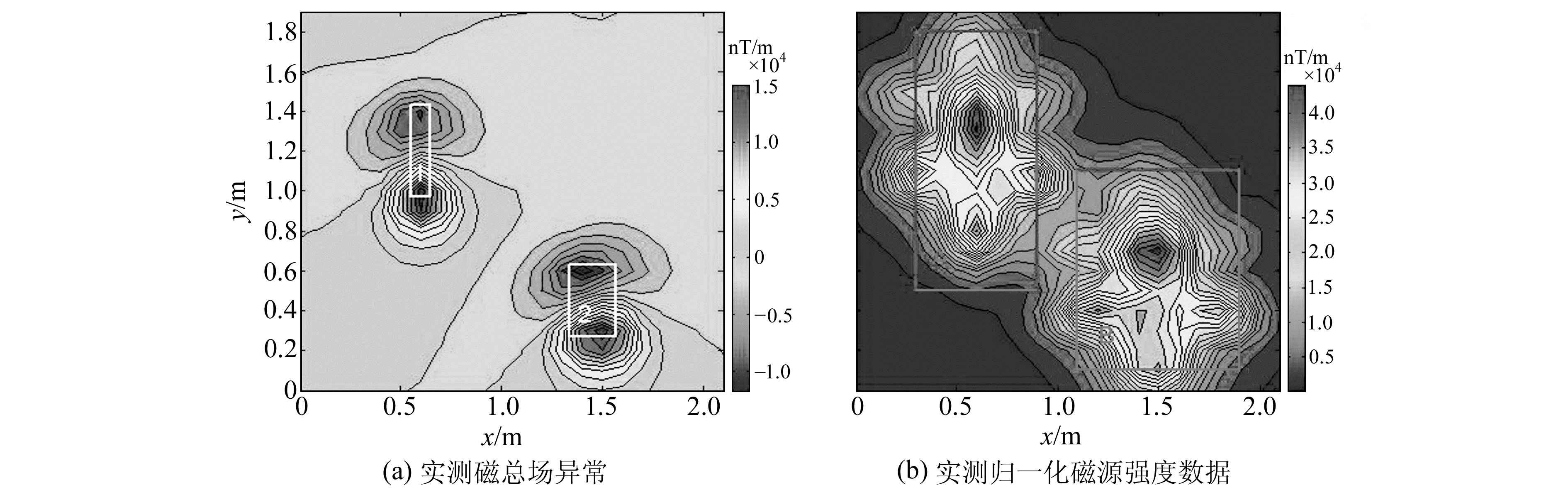
测区位于石家庄某地,在测区内分别放置铁磁性长方体和圆筒。由于这些铁磁性材料在制造过程中经过大量的锻造、轧制等工序,使得材料本身具有较强的剩余磁性。在地理坐标系下长方体1位于测区东南方向,中心坐标为(1.45, 0.45, 0.3),尺寸为0.23 m×0.36 m×0.2 m; 圆筒2位于测区西北方向,中心坐标为(0.6, 1.2, 0.3),圆筒直径为0.1 m,长为0.46 m。图 5展示了测量传感器阵列图,实验所用探头为利用Bartington公司生产的三轴磁通门传感器搭建的十字形磁梯度张量探头。该传感器的分辨率为0.1 nT,实测的仪器包括:十字形探头,数字采集模块以及软件操作终端。在实验过程中,将探头固定在无磁实验台架上,在台架的横向和纵向滑道上均标注了刻度值,利用扫描的方法对实测区域的每一点的磁梯度张量值进行测量。将地面的观测点划分为22×20=440个测点网格,每个测点间距为0.1 m。图 6(a)为磁总场异常实际测量数据,其中白色方框1、2为磁异常的实际水平分布;图 6(b)为归一化磁源强度异常实际测量数据,其中红色方框A、B为分块区域。实测区域的背景磁场的磁倾角为55.85°,磁偏角为-16.53°。取倾角I的范围为0°~90°、步长为1°,偏角D的范围为-90°~90°、步长为1°,计算A、B这2个分块场异常数据和归一化磁区域内的实测磁总源强度数据的互相关系数。经计算,得到A分块区域的磁倾角I为20°,D为-2°;B分块区域的磁倾角I为29°,D为-10°。由实验结果可知,A、B测区磁化方向估计值均与背景磁场磁化方向有较大差异,这是由于剩磁的存在导致背景磁化方向与总磁化方向不同。

|
图 5 实测区域及传感器阵列 Fig. 5 The actual measurement area and sensor array |
|
图 6 实测磁总场异常和归一化磁源强度数据 Fig. 6 The measured magnetic total field anomalies and measured normalized source strength data |
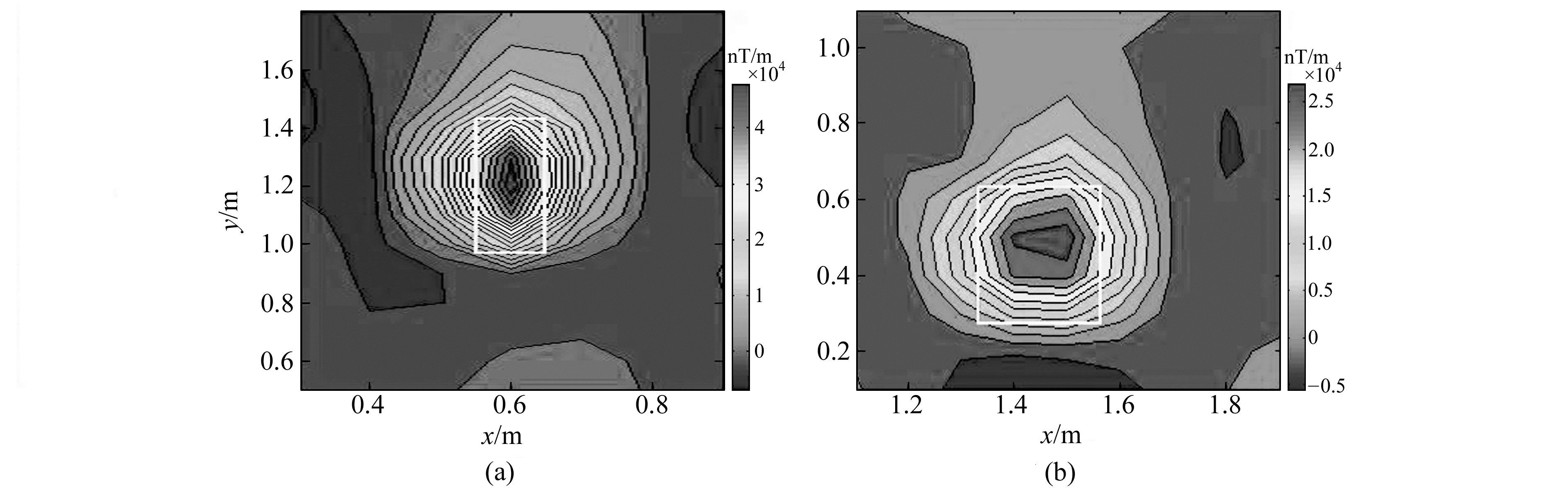
利用磁化方向估计结果对A、B测区进行化极处理,如图 7所示,其中白色部分为磁性异常体的理论位置。根据化极结果可以看出,异常体极大值位置与场源位置具有良好的对应关系,证明其估计结果与近等轴状异常源的总磁化方向相一致,进一步证明了本文方法的有效性。
|
图 7 利用估计的磁化方向对孤立磁源进行化极的数值 Fig. 7 Reduced-to-the-pole field for the individual anomalies, calculated for direction of magnetization equal to the estimated by the new method |
1) 提出了剩磁影响下磁性体磁化方向相关估计方法,即利用实测归一化磁源强度数据与实测磁总场化极数据进行互相关计算。仅需要对磁总场异常进行一次化极处理,无需对数据作其他的变换,计算过程稳定易行。
2) 归一化磁源强度数据是与磁化方向无关的量,其中心位置与垂直磁化条件下的磁总场异常具有较高的一致性,在含有强剩余磁化的条件下,能够准确地估计出异常源的磁化方向。
3) 通过仿真和实验证明,归一化磁源强度和磁总场模量互相关方法能准确地估计出近等轴状磁性体中总磁化方向。
| [1] |
刘双, 冯杰, 高文利, 等. 强剩磁强退磁条件下的二维井中磁测反演[J]. 地球物理学报, 2013, 56(12): 4297-4309 (Liu Shuang, Feng Jie, Gao Wenli, et al. 2D Inversion for Borehole Magnetic Data in the Presence of Significant Remanence and Demagnetization[J]. Chinese Journal Geophysics, 2013, 56(12): 4297-4309 DOI:10.6038/cjg20131232)
(  0) 0) |
| [2] |
Medeiros W E, Silva J B C. Simultaneous Estimation of Total Magnetization Direction and 3-D Spatial Orientation[J]. Geophysics, 60(5): 1365-1377 DOI:10.1190/1.1443872
(  0) 0) |
| [3] |
甘西. 利用微机确定磁性体磁化方向的行性探讨[J]. 湖北地矿, 2001, 15(1): 33-38 (Gan Xi. Feasibility of the Application of Microcomputer Method to the Magnetic Direction Determination of the Magnetic Body[J]. Hubei Geology & Mineral Resources, 2001, 15(1): 33-38 DOI:10.3969/j.issn.1671-1211.2001.01.006)
(  0) 0) |
| [4] |
Phillips J D. Can We Estimate Total Magnetization Directions from Aeromagnetic Data Using Helbig's Integrals[J]. Geophysics, 2005, 60(5): 1365-1377
(  0) 0) |
| [5] |
Dannemiller N, Li Y G. A New Method for Determination of Magnetization Direction[J]. Geophysics, 2006, 71(6): 69-73 DOI:10.1190/1.2356116
(  0) 0) |
| [6] |
Gerovska D, Arauzo-BravoM J, Stavrev P. Estimating the Magnetization Direction of Sources from Southeast Bulgaria Through Correlation between Reduced-to-the-Pole and Total Magnitude Anomalies[J]. Geophysical Prospecting, 2009, 57(4): 491-505 DOI:10.1111/gpr.2009.57.issue-4
(  0) 0) |
| [7] |
石磊, 孟小红, 郭良辉, 等. 剩磁影响下磁性体磁化方向估计的一种简单算法[J]. 地球物理学进展, 2014, 29(4): 1748-1751 (Shi Lei, Meng Xiaohong, Guo Lianghui, et al. A Simple Algorithm for Estimating the Magnetization Direction of Magnetic Bodies under the Influence of Remanent Magnetization[J]. Progress in Geophysics, 2014, 29(4): 1748-1751)
(  0) 0) |
| [8] |
郭良辉, 孟小红, 石磊, 等. 重力和重力梯度数据三维相关成像[J]. 地球物理学报, 2009, 52(4): 1098-1106 (Guo Lianghui, Meng Xiaohong, Shi Lei, et al. 3-D Correlation Imaging for Gravity and Gravity Gradiometry Data[J]. Chinese Journal of Geophysics, 2009, 52(4): 1098-1106 DOI:10.3969/j.issn.0001-5733.2009.04.027)
(  0) 0) |
| [9] |
郭良辉, 孟小红, 石磊. 磁异常△T三维相关成像[J]. 地球物理学报, 2010, 53(2): 435-441 (Guo Lianghui, Meng Xiaohong, Shi Lei. 3D Correlation for Magnetic Anomaly △T Data[J]. Chinese Journal Ofgeophysics, 2010, 53(2): 435-441 DOI:10.3969/j.issn.0001-5733.2010.02.022)
(  0) 0) |
| [10] |
孟小红, 刘国峰, 石磊, 等. 基于剩余异常相关成像的重磁物性反演方法[J]. 地球物理学报, 2012, 35(1): 304-309 (Meng Xiaohong, Liu Guofeng, Shi Lei, et al. 3-D Gravity and Magnetic Inversion for Physical Properties Based on Residual Anomaly Correlation[J]. Chinese Journal of Geophysics, 2012, 35(1): 304-309 DOI:10.6038/j.issn.0001-5733.2012.01.030)
(  0) 0) |
| [11] |
Beiki M, Clark D A, Austin J R, et al. Estimating Source Location Using Normalized Magnetic Source Strength Calculated from Magnetic Gradient Tensor Data[J]. Geophysics, 2012, 77(6): J23-J37 DOI:10.1190/geo2011-0437.1
(  0) 0) |
| [12] |
Blakely R J. Potential Theory in Gravity and Magnetic Applications[M]. Cambridge: Cambridge University Press, 1995
(  0) 0) |
2. High Speed Institute, Aerodynamic Research and Development Center, 6 South-Erhuan Road, Mianyang 621000, China;
3. PLA 65185 Troops, Tieling 112611, China
 2017, Vol. 37
2017, Vol. 37