2. 流域生态与地理环境监测国家测绘地理信息局重点实验室,南昌市广兰大道418号,330013;
3. 江西省数字国土重点实验室,南昌市广兰大道418号,330013
总体最小二乘[1]是顾及了系数矩阵误差的一种平差方法,是最小二乘的自然扩展。作为变量误差[2-5](errors-in-variables,EIV)模型的严密估计方法,总体最小二乘被广泛地应用。针对EIV模型,文献[6]基于高斯-牛顿法推导了加权总体最小二乘法,文献[7]推导了相关观测时的加权总体最小二乘法,文献[8]推导了附有约束条件的加权总体最小二乘法并将其应用到大地测量转换中,文献[9]和文献[10]推导了加权总体最小二乘算法,并对公式进行转换得到标准化最小二乘形式的参数表达式。顾及EIV模型系数矩阵中存在非随机元素及重复的随机元素,文献[11]对EIV模型系数矩阵进行分析,提出了将系数矩阵中重复的随机元素提取进行平差的partial errors-in-variables模型(Partial EIV模型);文献[12]对Partial EIV模型进行移项变化,使用两步间接平差的形式对模型进行解算,简化了参数的表达式且提高了计算效率;文献[13]针对相关情况推导了以随机误差平方和最小为准则的解法;文献[14]根据模型特点引入两个权比因子进行方差分量估计。然而,以上模型的算法均是在模型中系数矩阵是线性的前提下推导的。非线性问题是测量平差中常见的问题,非线性EIV模型的系数矩阵中的元素不再是独立的自变量,而是关于某一自变量的函数。多项式拟合模型是典型的非线性EIV模型,常见的多项式拟合模型有二次曲线回归模型[15]和三次回归模型[16]等。GPS高程拟合[17-20]模型也可用到多项式拟合,文献[18]在计算GPS高程拟合时是使用文献[21]构造系数矩阵权阵的方法进行平差,然而此时并不能反映出各元素的协因数;文献[15]针对非线性EIV模型推导了非线性总体最小二乘平差迭代算法,通过对模型线性化进行解算,然而在推导过程中是将函数模型整体作为非线性函数进行线性化,在形式上较为复杂。
基于上述分析,本文在Partial EIV模型构造思想的基础上,从构造随机向量的权阵角度出发,将多项式拟合模型系数矩阵中的自变量的函数作为随机元素提取,对自变量的函数进行二阶泰勒展开,根据协方差传播律得到自变量函数的协因数,结合Partial EIV模型的参数解算方法进行解算。这可以避免对整个平差模型线性化,只需要对系数矩阵中高次项元素进行泰勒展开,再根据协方差传播律获取随机元素的协因数就可进行平差解算,整体表达式更简洁,在一定程度上简化了计算程序。通过算例实验,使用Partial EIV模型进行解算得到的参数结果与文献[15]得到的参数结果相近,验证了方法的可行性。
1 多项式拟合模型的Partial EIV模型形式 1.1 多项式拟合模型多项式拟合模型的形式为:
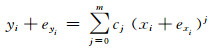
|
(1) |
式中,坐标xi、yi是通过观测手段获取的含有误差的观测值,exi、eyi分别表示其误差。因此,考虑一系列观测值,其对于m次拟合模型可以表达为:

|
(2) |
式中,当m=1时,模型为直线拟合模型,针对直线拟合模型已有较多的研究;当m=2时,模型为二次曲线回归模型,依此类推;m≥2时,模型为非线性EIV模型。
将式(2)写成向量形式有:
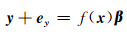
|
(3) |
式中,y为n×1观测量;ey为观测量误差;系数矩阵用函数f表示,且为自变量x的函数,x =[x1, x2, …, xn]T;β为待估参数。
1.2 Partial EIV模型Partial EIV模型是将系数矩阵中的随机元素提取,其数学模型如下:
1) 函数模型
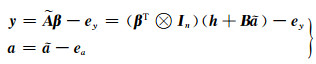
|
(4) |
2) 随机模型
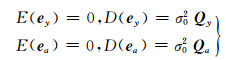
|
(5) |
式中,y为n×1观测量;ey为观测量误差;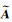
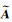
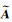
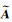
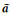
文献[15]将式(3)整体进行线性化,推导了非线性总体最小二乘平差迭代法。对多项式拟合模型进行分析可发现,其系数矩阵高次项都是自变量x的函数,根据Partial EIV模型的构造思想,将式(2)中高次项也作为独立的随机元素,可得到Partial EIV模型中向量a的形式为:

|
(6) |
式中,vec为矩阵拉直变换。继而可以得到矩阵B和列向量h的形式。将自变量的函数作为新的随机元素,并将随机元素提取就可得到与式(4)一样的函数模型。由文献[13]可知,对式(4)进行变形,并令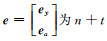
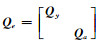
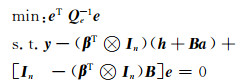
|
(7) |
构造拉格朗日函数并进行求偏导计算,并令C = 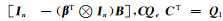
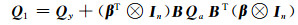
|
(8) |
经过公式推导计算[13],为将参数的表达式写成对称正定的矩阵形式,对其进行变化[12],最终得到参数估值的表达式为:
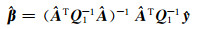
|
(9) |
式中,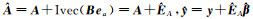
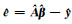
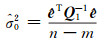
|
(10) |
在平差中关键是需要求解出向量a的协因数阵。对高次项进行二阶泰勒展开,再根据协方差传播律即可求得协方差。以xi2为例,在xi0处展开得:
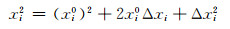
|
(11) |
因此可得到xi2的协方差为:
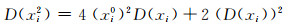
|
(12) |
由式(11)和式(12)可知,与以往只考虑一阶不同,增加二阶项的信息可以得到相对较精确的方差信息。在先验单位权方差σ02已知的情况下,即可得到xi2的协因数。
2 算例与分析 2.1 算例1GPS高程拟合模型[17-20]是多项式拟合模型,高程异常值与平面坐标的函数关系式可以表示为:
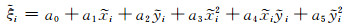
|
(13) |
式中,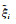
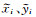
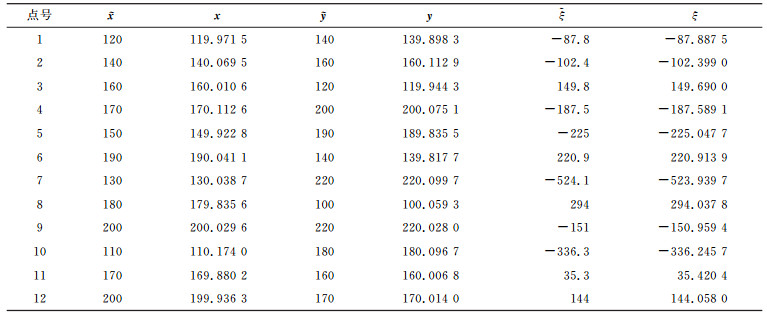
由式(13)可知,构造系数矩阵时,除去常数项,其余元素为向量x =[x1, x2, …, xi]T、y =[y1, y2, …, yi]T的函数。数据在文献[20]的基础上进行改化,给坐标真值和高程异常真值加入均值为0、中误差为0.1的随机误差,由MATLAB函数normrnd生成。坐标真值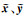
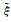
|
|
表 1 坐标观测值及高程异常 Tab. 1 The observation of coordinate and height anomaly |
文献[18]在计算高程拟合时使用的是文献[21]构造系数矩阵的总体最小二乘法,其系数矩阵的协因数阵构造形式为:
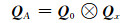
|
(14) |
式中,Q0=diag([0, 1, 1, 4x02, x02+y02, 4y02]T),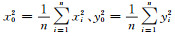
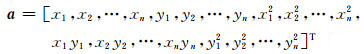
|
(15) |
计算向量a的协因数阵时,本文将系数矩阵中高次项作为独立的随机元素,忽略了元素之间的相关性,得到一种近似的解法。根据协方差传播律,其计算公式为:
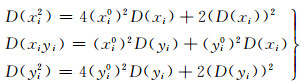
|
(16) |
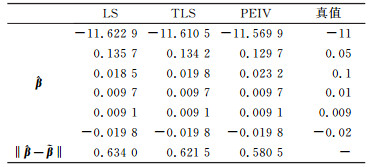
现分别用最小二乘(LS)、文献[10]的总体最小二乘法(TLS)及本文方法(PEIV)进行计算,得到参数估值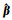
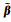
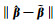
|
|
表 2 不同方法的解算结果 Tab. 2 Results from different methods |
从表 2可以看出,与以式(14)构造系数矩阵的协因数的总体最小二乘方法相比,将系数矩阵中的高次项作为随机元素提取进行Partial EIV模型的解算能得到更好的参数估值。这是因为,将高次项提取之后单独计算随机元素的协因数阵时可以更明显地体现出其权重信息,得到的差值范数分别为0.621 5和0.580 5。
2.2 算例2算例采用文献[15]的二次曲线回归模型:
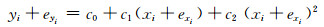
|
(17) |
其函数模型为:
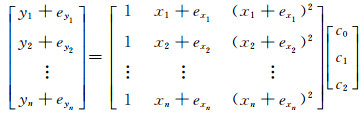
|
(18) |
坐标x和y的协因数阵为单位阵,参数的真值为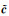
根据Partial EIV模型的解算思想,将系数矩阵中的随机元素提取作为一类观测值进行平差。因此,在二次曲线回归模型中,将xi、xi2作为随机元素,得到a的形式为:
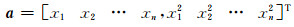
|
(19) |
式(19)中因为分别将高次项作为一类随机元素,因此可以简单地认为xi、xi2是相互独立的,其协因数阵的形式为对角阵;由式(12)可以求得xi2的协因数,继而得到协因数阵Qa、h、B的形式分别为:
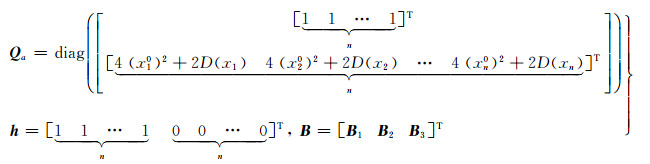
|
(20) |
其中,B1是n×2n的零矩阵,
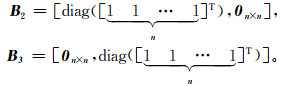
|
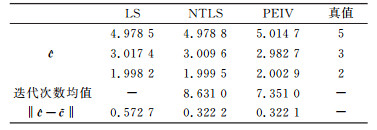
分别使用最小二乘(LS)、取均值构造系数矩阵并用文献[10]的总体最小二乘(TLS)、非线性总体最小二乘(NTLS)及本文方法(PEIV)进行参数解算,得到参数估值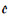
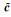
|
|
表 4 不同方法的解算结果 Tab. 4 The results from different methods |
从表 4可以看出,考虑了系数矩阵误差的总体最小二乘得到的差值范数要小于最小二乘,但由文献[21]构造系数矩阵使用总体最小二乘计算得到的参数结果并不理想。对于非线性总体最小二乘,将二次项xi2作为随机元素提取进行解算,可以得到与文献[15]进行线性化后相近的结果,参数估值与真值的差值范数分别为0.097 7和0.089 1。
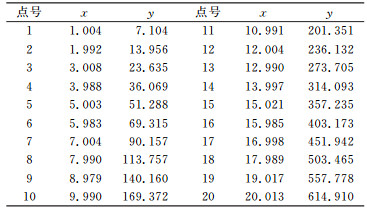
2.3 算例3为验证算法的可行性,模拟一个二次曲线回归模型同式(17),假设坐标x从0.5到10每隔0.5取一个点作为真值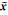
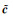
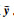
|
|
表 5 坐标真值 Tab. 5 The true value of coordinate |
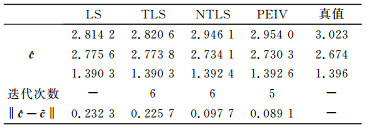
用MATLAB函数normrnd给坐标真值分别加上均值为0、中误差为0.05的随机误差,模拟计算1 000次,分别用最小二乘、NTLS和本文方法(PEIV)进行解算,得到1 000次结果的均值,见表 6。
|
|
表 6 不同方法的解算结果 Tab. 6 Results from different methods |
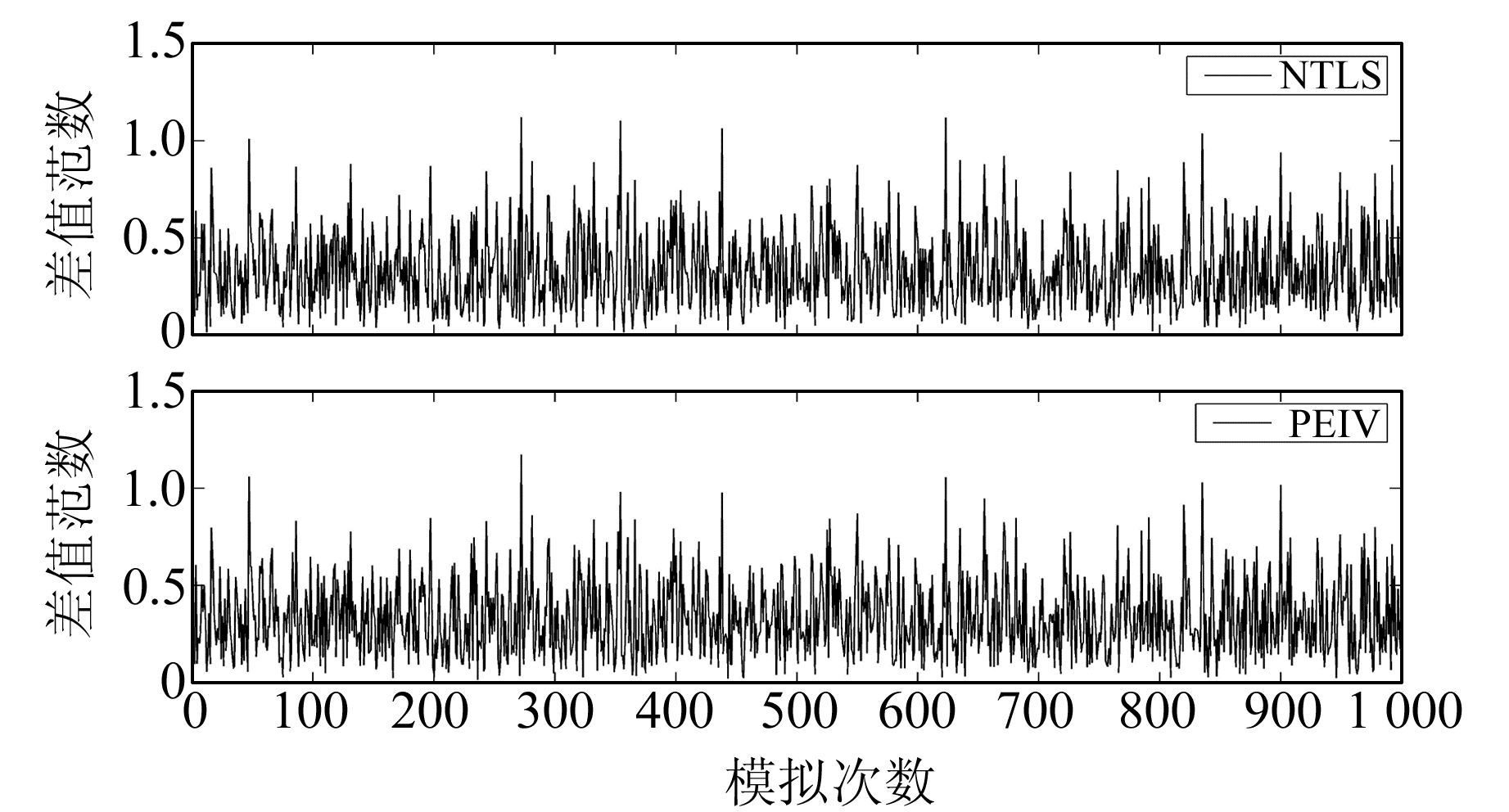
由表 6可以看出,本文方法(PEIV)计算得到的均值结果与NTLS方法计算得到的均值结果相近,最后得到的均值与真值的差值范数相差较小,且本文方法迭代次数的均值要少于NTLS方法。参数估值与真值的差值范数随模拟次数的变化见图 1。
|
图 1 参数估值与真值的差值范数 Fig. 1 The norm of difference with the estimated parameters and true value |
从图 1可以看出,两种方法计算得到的参数估值与真值的差值范数在模拟1 000次中每次都相近,计算得到的参数估值也相近。
3 结语本文通过分析多项式拟合模型系数矩阵的结构,根据Partial EIV模型提取系数矩阵随机元素的思想,将多项式拟合系数矩阵中自变量的函数也作为随机元素提取,采用Partial EIV模型的解法进行参数解算,新的随机元素的协因数阵可由已知的自变量协因数阵及协方差传播律获得,可以很好地反映出其信息。本文中以二次多项式为例,对二次项进行二阶泰勒展开,简化了计算过程。通过算例可以看出,本文方法计算结果与已有的非线性总体最小二乘的计算结果相近,说明将多项式拟合模型构造成Partial EIV模型形式求解是可行的。
| [1] |
Golub G H, Loan C F. An Analysis of the Total Least Squares Problem[J]. SIAM Journal on Numerical Analysis, 1980, 17(6): 883-893 DOI:10.1137/0717073
(  0) 0) |
| [2] |
王乐洋. 基于总体最小二乘的大地测量反演理论及应用研究[J]. 测绘学报, 2012, 41(4): 629 (Wang Leyang. Research on Theory and Application of Total Least Squares in Geodetic Inversion[J]. Acta Geodetica et Cartographica Sinica, 2012, 41(4): 629)
(  0) 0) |
| [3] |
王乐洋, 许才军. 总体最小二乘研究进展[J]. 武汉大学学报:信息科学版, 2013, 38(7): 850-856 (Wang Leyang, Xu Caijun. Progress in Total Least Squares[J]. Geomatics and Information Science of Wuhan University, 2013, 38(7): 850-856)
(  0) 0) |
| [4] |
刘经南, 曾文宪, 徐培亮. 整体最小二乘估计的研究进展[J]. 武汉大学学报:信息科学版, 2013, 38(5): 505-512 (Liu Jingnan, Zeng Wenxian, Xu Peiliang. Overview of Total Least Squares Methods[J]. Geomatics and Information Science of Wuhan University, 2013, 38(5): 505-512)
(  0) 0) |
| [5] |
Fang X, Wang J, Li B F, et al. On Total Least Squares for Quadratic Form Estimation[J]. Studia Geophysica et Geodaetica, 2015, 59(3): 366-379 DOI:10.1007/s11200-014-0267-x
(  0) 0) |
| [6] |
Shen Y Z, Li B F, Chen Y. An Iterative Solution of Weight Total Least-Squares Adjustment[J]. Journal of Geodesy, 2011, 85(4): 229-238 DOI:10.1007/s00190-010-0431-1
(  0) 0) |
| [7] |
Fang X. Weighted Total Least Squares Solutions for Applications in Geodesy[D]. Hannover: Leibniz Universität Hannover, 2011
(  0) 0) |
| [8] |
Fang X. Weight Total Least-Squares with Constraints: A Universal Formula for Geodetic Symmetrical Transformations[J]. Journal of Geodesy, 2015, 89(5): 459-469 DOI:10.1007/s00190-015-0790-8
(  0) 0) |
| [9] |
Jazaeri S, Amiri-Simkooei A R, Sharfi M A. Iterative Algorithm for Weight Total Least Squares Adjustment[J]. Survey Review, 2014, 46(334): 19-27 DOI:10.1179/1752270613Y.0000000052
(  0) 0) |
| [10] |
Amiri-Simkooei A R, Jazaeri S. Weighted Total Least Squares Formulated by Standard Least Squares Theory[J]. Jouranal of Geodetic Science, 2012, 2(2): 113-124
(  0) 0) |
| [11] |
Xu P L, Liu J N, Shi C. Total Least Squares Adjustment in Partial Errors-in-Variables Models: Algorithm and Statistical Analysis[J]. Journal of Geodesy, 2012, 86(8): 661-675 DOI:10.1007/s00190-012-0552-9
(  0) 0) |
| [12] |
王乐洋, 余航, 陈晓勇. Partial EIV模型的解法[J]. 测绘学报, 2016, 45(1): 22-29 (Wang Leyang, Yu Hang, Chen Xiaoyong. An Algorithm for Partial EIV Model[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(1): 22-29)
(  0) 0) |
| [13] |
许光煜. Partial EIV模型的总体最小二乘方法及应用研究[D].南昌: 东华理工大学, 2016 (Xu Guangyu. The Total Least Squares Method and Its Application of Partial Errors-in-Variables Model[D]. Nanchang: East China University of Technology, 2016) http://cdmd.cnki.com.cn/Article/CDMD-10405-1015990518.htm
(  0) 0) |
| [14] |
Wang L Y, Xu G Y. Variance Component Estimation for Partial Errors-in-Variables Models[J]. Studia Geophysica et Geodaetica, 2016, 60(1): 35-55 DOI:10.1007/s11200-014-0975-2
(  0) 0) |
| [15] |
胡川, 陈义. 非线性整体最小平差迭代算法[J]. 测绘学报, 2014, 43(7): 668-674 (Hu Chuan, Chen Yi. An Iterative Algorithm for Nonlinear Total Least Squares Adjustment[J]. Acta Geodetica et Cartographica Sinica, 2014, 43(7): 668-674)
(  0) 0) |
| [16] |
Mahboub V, Aradalan A A, Ebrahimzadeh S. Adjustment of Non-Typical Errors-in-Variables Models[J]. Acta Geodaetica et Geophysica, 2015, 50(2): 207-218 DOI:10.1007/s40328-015-0109-5
(  0) 0) |
| [17] |
赵辉, 张书毕, 张秋昭. 基于加权总体最小二乘法的GPS高程拟合[J]. 大地测量与地球动力学, 2011, 31(5): 88-96 (Zhao Hui, Zhang Shubi, Zhang Qiuzhao. GPS Height Fitting of Weighted Total Least-Squares Adjusting[J]. Journal of Geodesy and Geodynamics, 2011, 31(5): 88-96)
(  0) 0) |
| [18] |
袁豹, 岳东杰. 加权总体最小二乘法及其在GPS高程拟合中的应用[J]. 勘察科学技术, 2013(2): 43-45 (Yuan Bao, Yue Dongjie. Application of Weighted Total Least-Squares Method in GPS Elevation Fitting[J]. Site Investigation and Technology, 2013(2): 43-45 DOI:10.3969/j.issn.1001-3946.2013.02.011)
(  0) 0) |
| [19] |
丁海勇, 孙景领. GPS高程转换的总体最小二乘方法研究[J]. 大地测量与地球动力学, 2013, 33(3): 52-55 (Ding Haiyong, Sun Jingling. Research on Total Least-Squares Methods for Transformation of GPS Elevation[J]. Journal of Geodesy and Geodynamics, 2013, 33(3): 52-55)
(  0) 0) |
| [20] |
王乐洋, 吴飞, 吴良才. GPS高程转换的总体最小二乘拟合推估模型[J]. 武汉大学学报:信息科学版, 2016, 41(9): 1259-1264 (Wang Leyang, Wu Fei, Wu Liangcai. Total Least Squares Fitting Estimation Model for GPS Height Transformation[J]. Geomatics and Information Science of Wuhan University, 2016, 41(9): 1259-1264)
(  0) 0) |
| [21] |
Schaffrin B, Wieser A. On Weighted Total Least Squares Adjustment for Linear Regression[J]. Journal of Geodesy, 2008, 82(7): 415-421 DOI:10.1007/s00190-007-0190-9
(  0) 0) |
2. Key Laboratory of Watershed Ecology and Geographical Environment Monitoring, NASMG, 418 Guanglan Road, Nanchang 330013, China;
3. Key Lab for Digital Land of Jiangxi Province, 418 Guanglan Road, Nanchang 330013, China
 2017, Vol. 37
2017, Vol. 37