2. 北京卫星导航中心, 北京市, 100094;
3. 61876部队,三亚市, 572022
广播星历参数是卫星导航电文的主要内容之一,其选择和设计决定广播星历所能达到的精度以及用户算法的复杂程度[1]。GPS采用开普勒根数与其摄动变化量组成的广播星历参数,包括1个参考时刻、6个参考时刻的开普勒根数、6个短周期调和改正项振幅、3个长期项改正数共16个参数。考虑到半长径和偏心率在地球非球形引力项J22的影响下存在长周期变化,GPS后续发展的新型卫星的民用导航电文在原来16参数模型基础上,引入半长径长期变率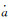
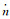
BDS采用物理意义明确、外推能力强、数据量小、用户计算量适中的类GPS开普勒根数广播星历[4],BDS的GEO卫星具有小倾角、小偏心率的特性。在小倾角条件下,轨道升交点赤经Ω和近地点角距ω无法严格区分,在小偏心条件下,平近点角M和近地点角ω无法严格区分,因此采用开普勒轨道根数模型进行星历拟合,存在小倾角和小偏心率奇异问题[5]。采用基于旋转坐标面的星历拟合的方法,可以消除GEO卫星轨道小倾角的奇异性问题[6]。北斗区域导航系统ICD采用此法,星历拟合前将三维位置误差绕X轴旋转5°,用户计算卫星位置时需反向旋转5°恢复GEO轨道的正确定向[7]。ICD文件中对绕坐标轴旋转角度的大小没有特别说明选择依据,实际系统组网运行中发现,在特定时段,GEO广播星历部分参数在编码导航电文时超过该参数的比特位限制[1]。在小偏心率条件下,当偏心率小于0.000 1时,星历拟合迭代次数剧增,并出现拟合失败情况。将18参数模型应用到北斗GEO卫星,虽然拟合精度更高,但参数相关性强,拟合不稳定的问题更加突出[5]。
第一类无奇点根数采用偏心率向量代替偏心率和近地点角距,克服小偏心率奇异问题,又能保证与开普勒轨道根数的精确转换,因此在导航卫星星历拟合中得到广泛应用[5, 8-9]。本文将第一类无奇点根数和坐标旋转方法综合运用到GEO卫星的18参数星历拟合,并对北斗在轨GEO卫星的星历拟合结果的拟合精度和稳定性进行长期分析评估,定量分析GEO卫星处于春分和秋分两个地影季时,星历拟合精度衰减程度。针对Δn参数超限的问题,比较绕X轴旋转5°和旋转55°时Δn参数的变化范围。
1 广播星历拟合模型 1.1 第一类无奇点根数拟合算法设原始开普勒轨道根数为σ0,其定义为:
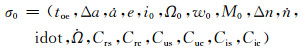
|
(1) |
无奇点根数定义为:
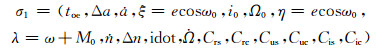
|
(2) |
采用无奇点根数模型拟合广播星历,可以消除小偏心率引起的奇点问题,同时该参数能精确转换成开普勒轨道根数,保证用户算法不变。拟合过程为:由参考历元的卫星三维位置速度计算开普勒根数并赋值给σ0,将σ0转换为无奇点根数σ1作为迭代初值,迭代过程中计算偏导数采用无奇点根数σ1消除奇异性,计算观测残差采用原始开普勒参数σ0,保证在标准用户算法下迭代收敛。偏导数及计算过程参见文献[5]。
将式(2)中17个参数(除toe)作为待求参数,对观测方程进行展开,舍去二阶及以上小量得线性化观测方程,其矢量形式表示如下:
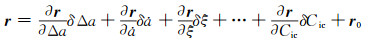
|
(3) |
式中,r为观测历元t时刻地固坐标系下的卫星位置向量;r0为计算的卫星位置向量近似值; δΔa、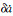
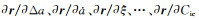
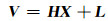
|
(4) |
式中,V为3 k维残差向量;H为3 k×17维系数矩阵;L为3 k维观测向量。当满足3 k≥17时,由最小二乘估计原理计算星历参数的修正值。
参数收敛条件设置为:
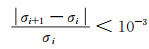
|
(5) |
式中,σi是第i次迭代的单位权中误差。
1.2 坐标系旋转方法小倾角奇异不是本质奇点,是所选惯性坐标系下轨道根数表达的奇异性,可以通过选择不同的参考面来解决。
1) 以星历参考时刻toe的地固系为准惯性系,将地固系中的卫星位置序列通过绕Z轴顺时针旋转θk转换到准惯性坐标系下:
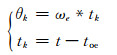
|
(6) |
式中,ωe为地球自转角速度,t为历元时刻。
2) 在准惯性坐标系下,绕X轴顺时针旋转n得到新惯性系下的卫星位置序列。
3) 在新惯性坐标系下拟合星历。
1.3 综合第一类无奇点根数与坐标旋转的星历拟合方法1) 计算初始轨道根数。以星历参考时刻toe的地固系为准惯性系,设R0和V0分别为地固系下的位置和速度向量,准惯性系下卫星位置向量R1为原始地固系位置向量R0,速度向量需顾及地球自转速度,见式(7)。将R1和V1绕X轴顺时针旋转n得到新惯性系下toe时刻的卫星位置和速度向量R′1和V′1:
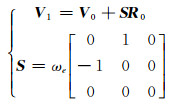
|
(7) |
2) 将卫星在地固系下的位置序列转换到新惯性坐标系下,方法见§1.2。
3) 在新惯性坐标系下进行第一类无奇点根数星历拟合。
2 结果与讨论利用国内区域监测网2013年全年的伪距相位数据进行多星多站联合精密定轨,同时解算所有卫星轨道参数(初轨、光压及经验加速度)、接收机模糊度参数、大气天顶延迟和各历元卫星与接收机钟差参数。定轨弧长为3 d,预报弧长为8 d(数值轨道弧长为11 d),每10 d进行一次精密定轨,共计进行36次精密定轨,数值轨道覆盖2013年全年。为分析拟合精度与弧长的关系,采用1 h滑动窗口、2~6 h弧长的拟合弧长对在轨13颗卫星进行全年星历参数拟合。
2.1 拟合精度星历拟合精度通常利用拟合URE评估,URE是利用导航卫星广播的卫星星历和钟差计算的卫星位置误差和钟差误差在用户和卫星视线方向的投影,URE来源主要是外推轨道和钟差误差,还包括星历参数拟合和钟参数拟合的拟合误差。仅分析星历拟合URE为:

|
(8) |
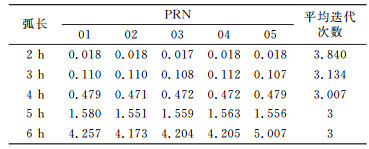
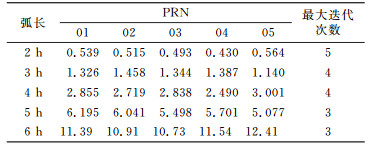
从全年拟合结果看,该方法能成功对GEO卫星进行星历拟合,全年无拟合失败的情况,避免倾角小于0.01°或偏心率小于0.000 1时常规拟合方法拟合失败的问题。表 1和表 2给出所有在轨GEO卫星拟合URE全年平均值和最大值,可以看出,随着拟合弧长的增加,拟合精度降低,2~4 h拟合弧段最大RMS为3 cm;在相同的拟合弧段内,各颗GEO的星历拟合URE的RMS平均值和最大值具有相同量级,且数值差异较小。5颗在轨GEO卫星全年拟合无迭代发散情况,平均和最大迭代次数随着拟合弧长增加而减小。当拟合弧长为2 h时,最大迭代次数为5次,平均迭代次数为3.840次,表明综合无奇点根数和坐标旋转的星历拟合方法即使采用较短的2 h拟合弧长,拟合稳定性也较高。当拟合弧长为5 h和6 h时,所有卫星拟合迭代次数都为3次。
|
|
表 1 星历拟合URE的RMS 2013年全年平均值 Tab. 1 Average RMS of the fitting URE throughout 2013 |
|
|
表 2 星历拟合URE RMS 2013年全年最大值 Tab. 2 Max RMS of the fitting URE throughout 2013 |
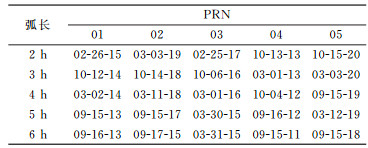
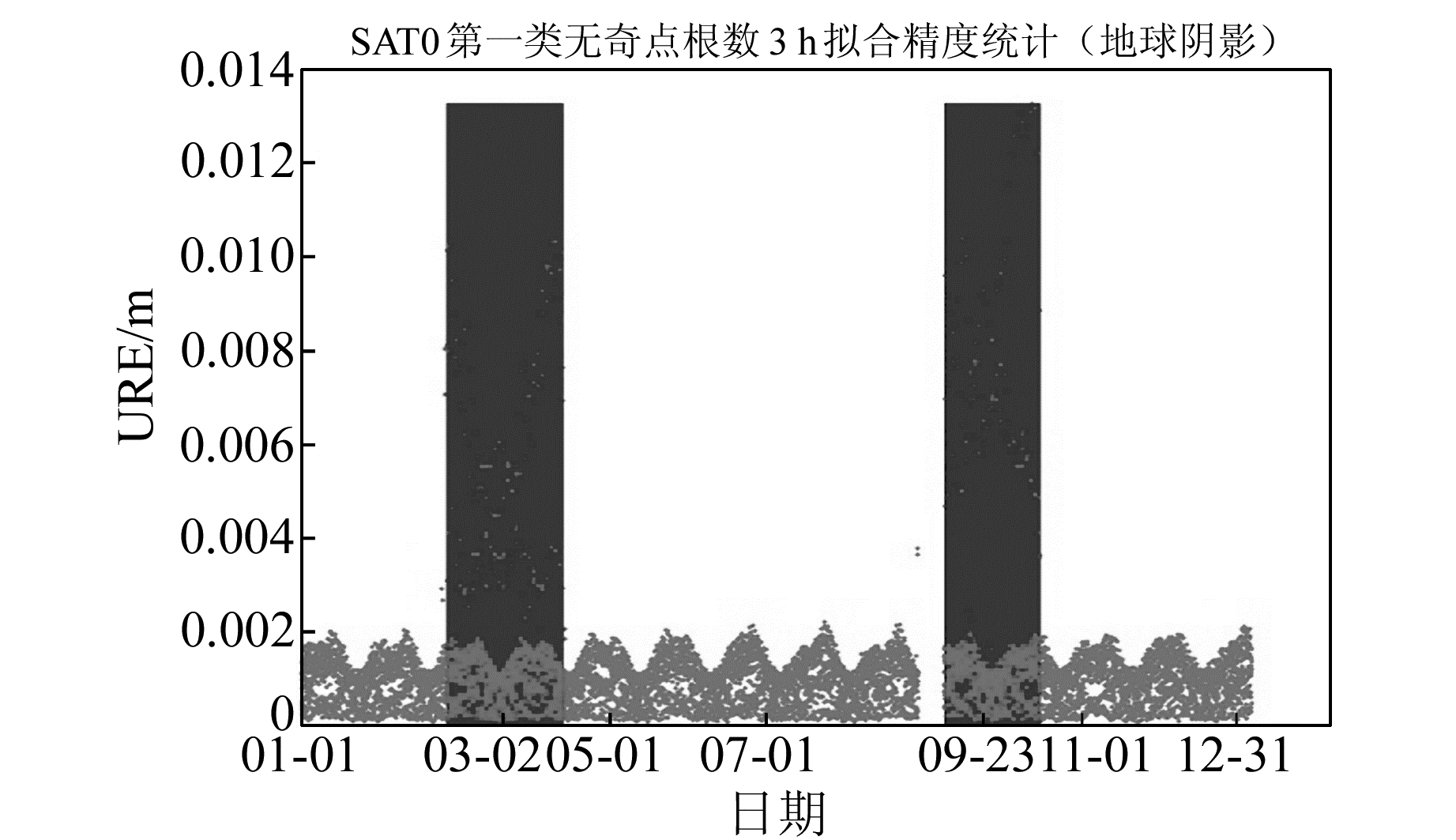
地影指太阳、地球和卫星运行至几乎同一平面时,受地球遮挡,卫星星体不能接受到太阳光线照射并感知太阳位置的现象。对于静止轨道卫星,当太阳赤纬绝对值小于8.424°时,将发生地影,发生地影的时间大约是从02-27~04-12和08-31~10-16,全年约92 d,且地影持续时间最长可达72 min[10]。图 1列出PRN01卫星全年星历拟合的URE序列,其中两个阴影区域分别为春分和秋分两个地影季,结果表明,即使在地影季,若拟合弧段不包含地影时段,卫星所受光压辐射连续无间断,故星历拟合精度不受影响。当拟合弧段包含地影时段时,光压间断性影响轨道数据平滑性,导致星历拟合精度降低。表 3给出各颗卫星最大拟合误差对应的toe时刻,表明最大拟合误差发生在春分或秋分地影季。
|
图 1 PRN01 3 h星历拟合URE序列 Fig. 1 URE RMS time series of 3 h fitting of PRN01 |
|
|
表 3 最大拟合误差对应toe时刻 Tab. 3 The toe epoch with respect to the max RMS of the fitting error |
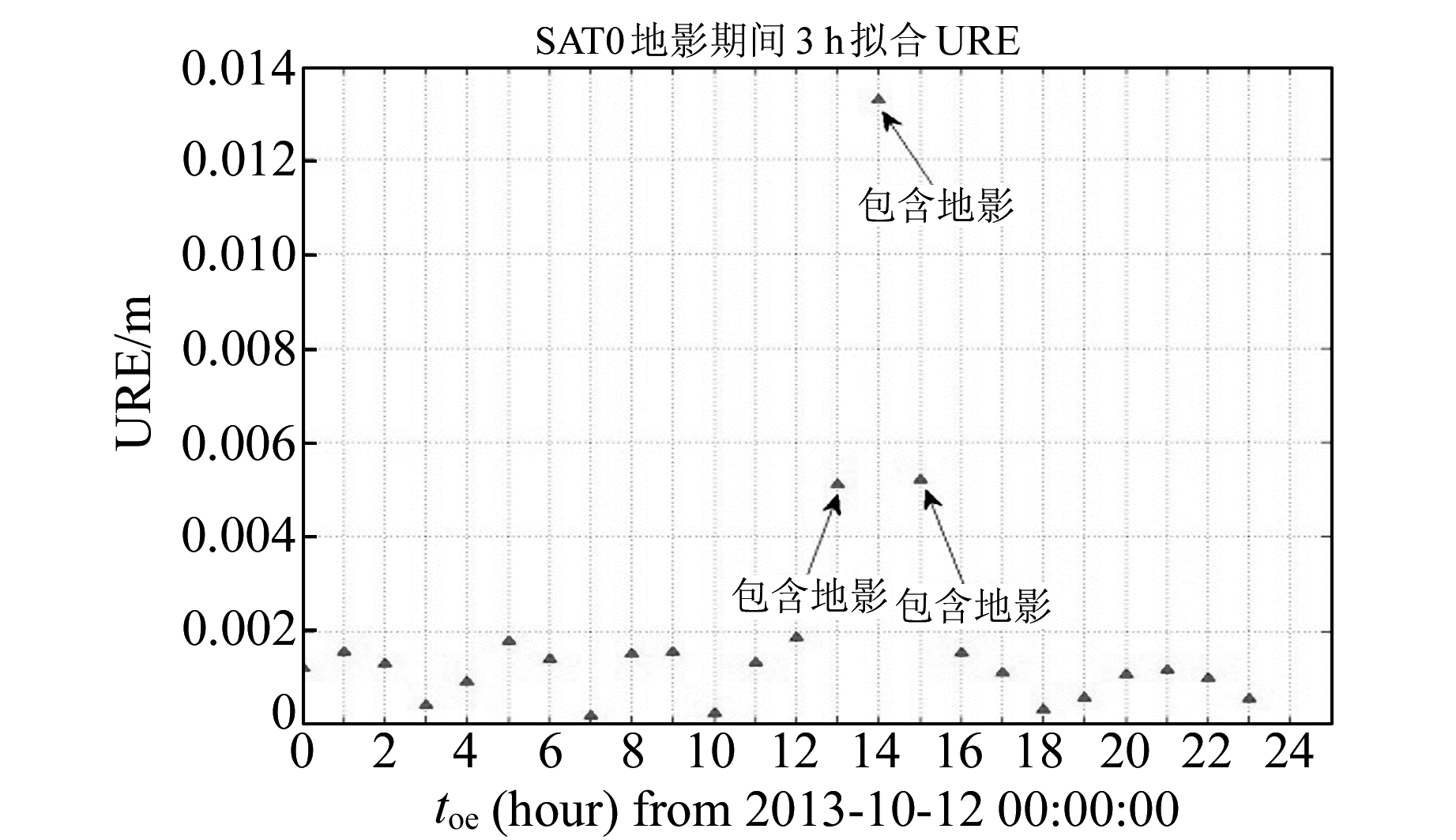
按照锥形地影模型[10]计算得到2013-10-12 PRN01卫星14:04~14:45时段处于地球阴影中,其余时段被太阳照射,当拟合弧段为3 h时,会有3 h的星历拟合精度受影响,如图 2所示。
|
图 2 PRN01 2013-10-12拟合URE Fig. 2 URE RMS of 3 h fitting of PRN01 |
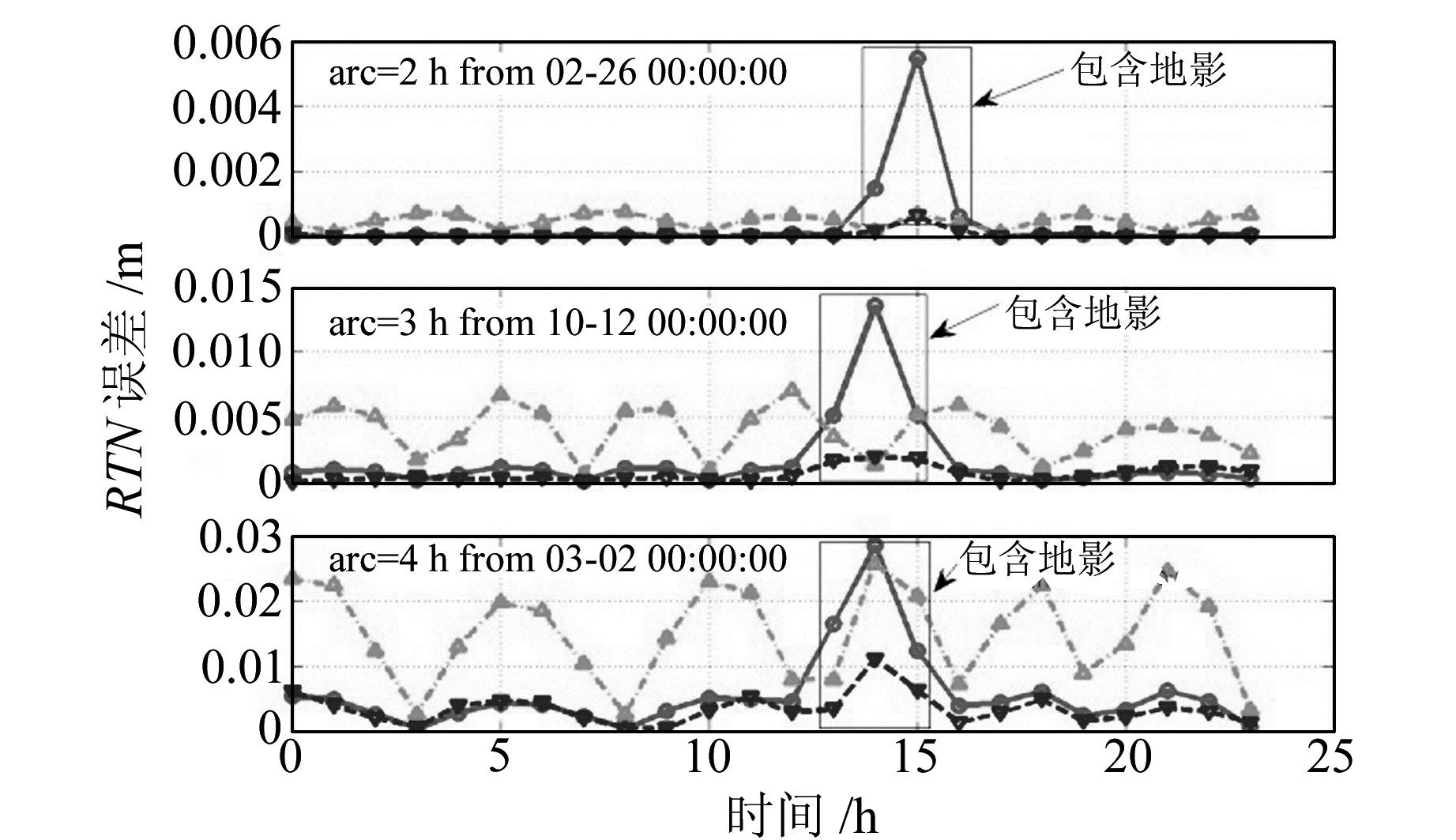
图 3和图 4分别给出PRN01和PRN04卫星全年最大拟合URE误差的全天拟合误差分量,图中实线代表R方向误差,虚线代表T方向误差,点线代表N方向误差,矩形区域代表拟合弧段包含进出地影的卫星轨道。
|
图 3 PRN01地影季全天拟合RTN误差 Fig. 3 URE RMS of PRN01 in an eclipse season day |

|
图 4 PRN04地影季全天拟合RTN误差 Fig. 4 URE RMS of PRN04 in an eclipse season day |
从图 3和图 4看出,当拟合弧段不包含地影数据时,T方向星历拟合误差最大,R和N方向误差较小;当拟合弧段包含地影时,R方向拟合误差显著增大,T和N方向拟合误差增大不显著,当弧长较短如3 h时,R方向拟合误差甚至远远超过T方向拟合误差,随着拟合弧长增加,拟合误差增大。由于地影占整个弧段比例变小,地影对星历拟合的影响变小。
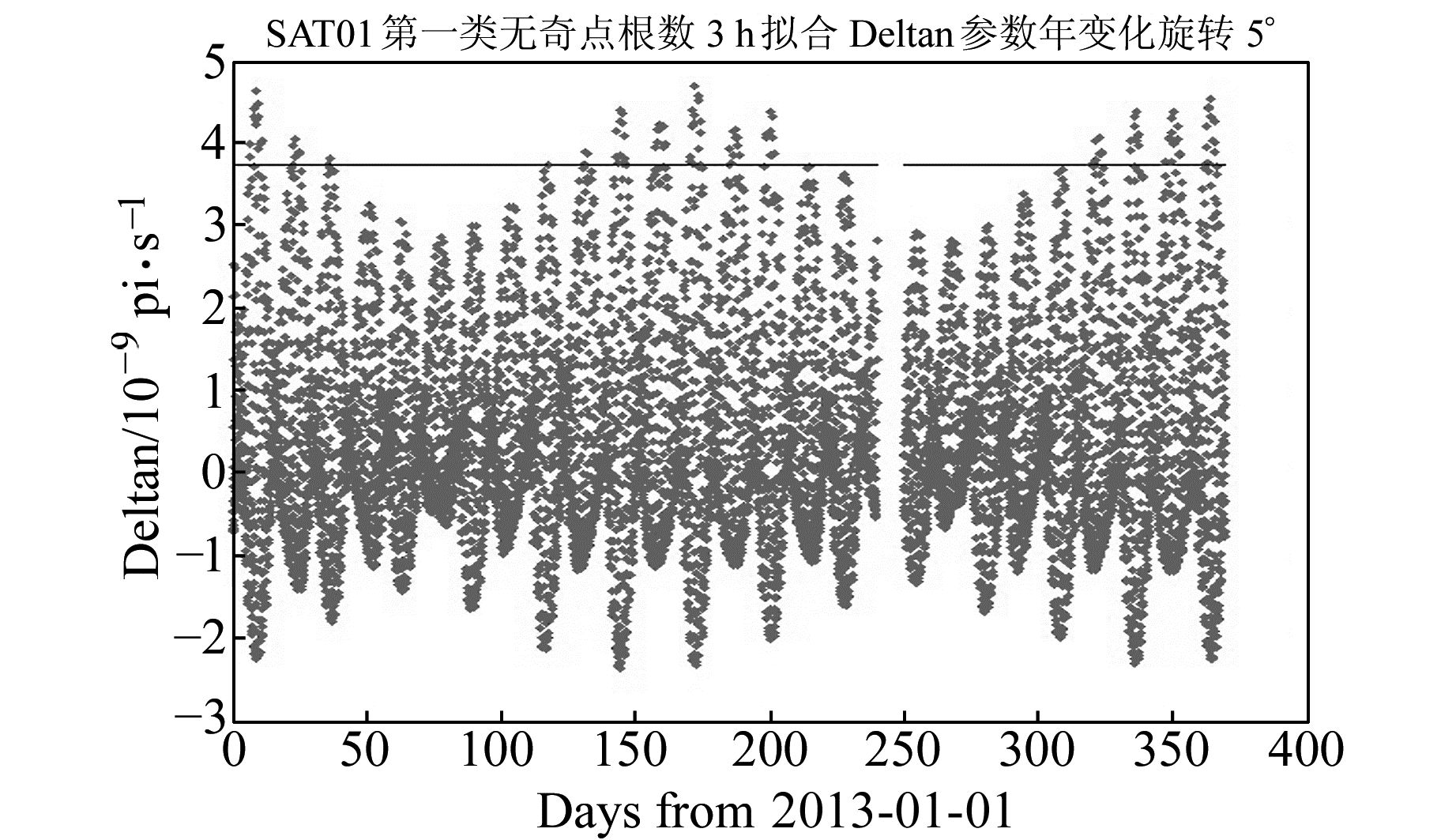
2.3 参数变化范围北斗ICD文件规定了Δn参数的表达范围为[-3.73×10-9π/s, 3.73×10-9π/s],针对GEO卫星星历拟合过程中Δn参数在特定时段存在超过接口表达范围的问题,文献[1]基于北斗现行16参数模型对GEO卫星进行为期1个月的星历拟合,通过对Δn参数的规律分析,月球摄动力和解算方程病态性的综合因素导致拟合参数超限。采用18参数的星历拟合模型,Δn参数是否还存在参数超限问题?若仍按照ICD规定的对GEO卫星绕X旋转5°方法进行拟合,Δn参数序列如图 5所示,部分时段存在参数超限现象。文献[6]通过理论推导和实验验证得到的GEO卫星星历参数Δn和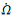
|
图 5 PRN01星历拟合Δn序列(旋转5°) Fig. 5 Deltan time series of PRN01 from 3 h fit (5° rotation) |

|
图 6 PRN01星历拟合Δn序列(旋转55°) Fig. 6 Deltan time series of PRN01 from 3 h fit (55° rotation) |
针对北斗GEO卫星同时具有小偏心率和小倾角的特点,将无奇点根数和坐标旋转方法综合运用到GEO卫星的18参数星历拟合,同时解决GEO卫星的小偏心率奇点和小倾角奇点问题。基于北斗5颗在轨GEO卫星1 a的实际轨道数据对该方法进行分析与论证,得出以下结论:
1) 该方法能成功对GEO卫星进行星历拟合,全年无拟合失败的情况;从2~6 h弧长拟合实验来看,拟合弧长越长,迭代次数越少,当拟合弧长为2 h时,最大迭代次数为5次,平均迭代次数为3.840次,表明该方法即使采用较短拟合弧长,拟合稳定性也较高。
2) 精度拟合弧长越长拟合精度越低,2~4 h拟合弧长时5颗GEO卫星的星历拟合精度最大仅为3 cm。
3) 当拟合弧段包含进出地影轨道时,拟合精度降低,所有在轨GEO卫星的全年拟合最大误差发生在地影期间。
4) 不同旋转角度将影响拟合参数变化范围,旋转55°比旋转5°的Δn参数变化范围减少一个数量级,Δn参数全年无超限现象。
| [1] |
何峰, 王刚, 刘利, 等. 地球静止轨道卫星广播星历参数拟合与试验分析[J]. 测绘学报, 2011, 40(增1): 52-58 (He Feng, Wang Gang, Liu Li, et al. Ephemeris Fitting and Experiments Analysis of GEO Satellite[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(S1): 52-58)
(  0) 0) |
| [2] |
黄华, 刘林, 周建华, 等. 18参数广播星历分析研究[J]. 飞行器测控学报, 2012, 31(3): 80-84 (Huang Hua, Liu Lin, Zhou Jianhua, et al. Research on 18 Elements Broadcast Ephemeris Model[J]. Journal of Spacecraft TT & C Technology, 2012, 31(3): 80-84)
(  0) 0) |
| [3] |
Du L, Zhang Z K, Zhang J, et al. An 18-Element GEO Broadcast Ephemeris Based on Non-Singular Elements[J]. GPS Solutions, 2015, 19(1): 49-59 DOI:10.1007/s10291-014-0364-x
(  0) 0) |
| [4] |
阮仁桂, 贾小林, 吴显兵, 等. 关于坐标旋转法进行地球静止轨道导航卫星广播星历拟合的探讨[J]. 测绘学报, 2011, 40(5): 145-150 (Ruan Rengui, Jia Xiaolin, Wu Xianbing, et al. Broadcast Ephemeris Parameters Fitting for GEO Satellites Based on Coordinate Transformation[J]. Acta Geodaetica et Cartogrphica Sinica, 2011, 40(5): 145-150)
(  0) 0) |
| [5] |
黄华.导航卫星广播星历参数模型及拟合算法研究[D].南京: 南京大学, 2012 (Huang Hua. Research on the Broadcast Ephemeris Parameters Model and Its Fitting Algorithm[D]. Nanjing: Nanjing University, 2012) http://cdmd.cnki.com.cn/article/cdmd-10284-1012376108.htm
(  0) 0) |
| [6] |
黄勇, 胡小工, 王小亚, 等. 中高轨卫星广播星历精度分析[J]. 天文学进展, 2006, 24(1): 81-87 (Huang Yong, Hu Xiaogong, Wang Xiaoya, et al. Precision Analysis of Broadcast Ephemeris for Medium and High Orbit Satellite[J]. Process in Astronomy, 2006, 24(1): 81-87 DOI:10.3969/j.issn.1000-8349.2006.01.008)
(  0) 0) |
| [7] |
张中凯, 杜兰, 刘利, 等. GEO广播星历参数设计的无奇点根数法[J]. 测绘学报, 2014, 43(5): 452-457 (Zhang Zhongkai, Du Lan, Liu Li, et al. Parameter Design of GEO Broadcast Ephemeris Based on the Nonsingular Orbital Elements[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(5): 452-457)
(  0) 0) |
| [8] |
文援兰, 刘光明, 张志. 基于无奇异变换的卫星广播星历拟合算法[J]. 宇航学报, 2011, 32(12): 2478-2483 (Wen Yuanlan, Liu Guangming, Zhang Zhi. Research on the Fitting Algorithm of Broadcast Ephemeris Parameters Based on Non-singular Transformation[J]. Journal of Astronautics, 2011, 32(12): 2478-2483 DOI:10.3873/j.issn.1000-1328.2011.12.002)
(  0) 0) |
| [9] |
韩星远, 向开恒, 王海红. 第一类无奇点变量的广播星历参数拟合算法[J]. 航天器工程, 2011, 20(4): 54-59 (Han Xingyuan, Xiang Kaiheng, Wang Haihong. Research on Broadcast Ephemeris Parameters Fitting Algorithm Based on the First Class of No Singularity Variables[J]. Spacecraft Engineering, 2011, 20(4): 54-59 DOI:10.3969/j.issn.1673-8748.2011.04.009)
(  0) 0) |
| [10] |
毛悦, 宋小勇, 贾小林, 等. 北斗导航卫星地影状态分析[J]. 测绘学报, 2014, 43(4): 353-359 (Mao Yue, Song Xiaoyong, Jia Xiaolin, et al. Earth Eclipse Status Analysis of Beidou Navigation Satellite[J]. Acta Geodaetica et Cartographica Sinnica, 2014, 43(4): 353-359)
(  0) 0) |
2. Beijing Satellite Navigation Center, Beijing 100094, China;
3. PLA 61876 Troops, Sanya 572022, China
 2017, Vol. 37
2017, Vol. 37