2. 中国科学院上海天文台,上海市南丹路80号,200030
监测地球物理现象(如地震、火山喷发、地面沉降等)所引发的地表形变场,对于准确认识地球物理现象的发生机制、运动过程和发展趋势具有重要的数据支撑作用[1]。目前,常用的大范围地表形变监测方法主要有全球卫星定位系统(GPS)和合成孔径雷达干涉测量技术(InSAR)[2-3]。利用GPS观测数据可以获得测站高精度的东(E)、北(N)、垂直(U)方向的位移。但是,GPS数据空间分辨率低,难以满足大区域变形分析的要求,而且监测系统成本高。InSAR技术具有空间分辨率高、覆盖范围广等优点,可以获取大范围同震形变场,弥补GPS测量空间分辨率低的不足,但只能获取视线向的一维变形。基于InSAR与GPS数据融合的地表位移监测方法,可以最大化结合两者优点,适用于地震、滑坡等区域的高时空分辨率、高精度的地表位移监测[4]。
2011-03-11日本本州东海岸附近海域发生MW9.0大地震,震中位于(38.322°N,142.369°E),此次地震由太平洋板块向日本海沟下方俯冲并向西侵入欧亚板块造成[5]。为了更好地研究震源机制及其震后响应,详细的空间同震位移场分布极其重要。InSAR形变结果的精度受到很多因素的影响,主要包含干涉失相干、DEM误差、轨道误差以及大气延迟等。本文针对轨道误差,研究其对同震位移的影响及其去除方法。利用震区地面的GPS观测位移数据与InSAR获取的LOS向位移比对,拟合轨道误差改正模型参数,并讨论雷达入射角对轨道误差改正的影响,从而去除InSAR形变数据中的卫星轨道误差,得到该地震高精度的InSAR同震形变场。
1 轨道误差校正模型对于Tohoku地震,DEM误差与大气延迟误差对LOS向形变量影响相对较小(< 5 cm),可忽略不计[6]。但是,其中轨道误差对地表形变精度的影响不可忽视。
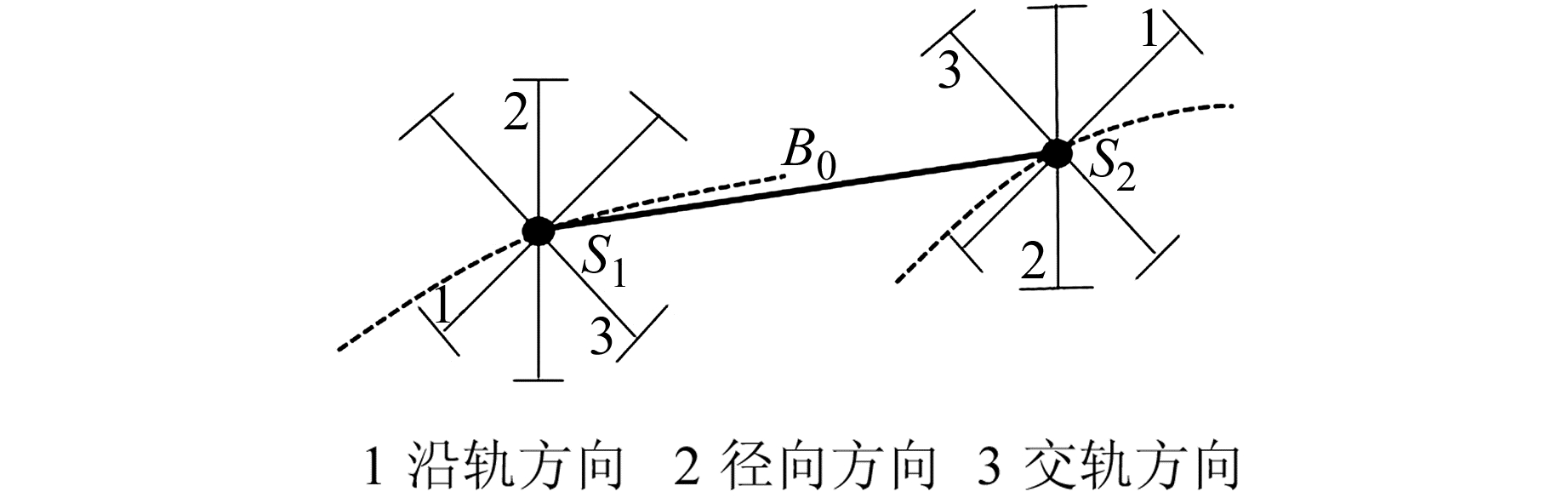
轨道误差向量通常包含沿轨、径向和交轨方向误差(图 1),其中,沿轨方向误差一般在影像配准阶段得到校正,而交轨方向和径向误差作为系统误差在干涉处理过程中传递到干涉相位中[7]。
|
图 1 轨道误差方向 Fig. 1 Direction of orbit error |
轨道误差对LOS向形变值的影响表现为基线误差对参考相位和高程相位的影响两部分,可以通过下式表示:
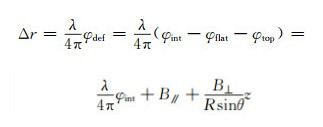
|
(1) |
式中,λ为雷达波长;φdef为形变相位;φint为干涉相位;φflat为地平相位;φtop为地形相位;R为地球半径;z为地形高度;B//为干涉基线在雷达视线方向的投影;B⊥为干涉基线在垂直雷达视线方向的投影;θ表示雷达侧视角。
图 2中,B0为真实基线,采用一个噪声向量n表示轨道误差,将其在平行与垂直基线方向上分解为n//与n⊥,在水平与竖直方向上分解为nh与nv;B为包含轨道误差的观测基线。由图 2所示几何关系可得:
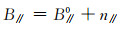
|
(2) |
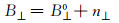
|
(3) |
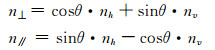
|
(4) |
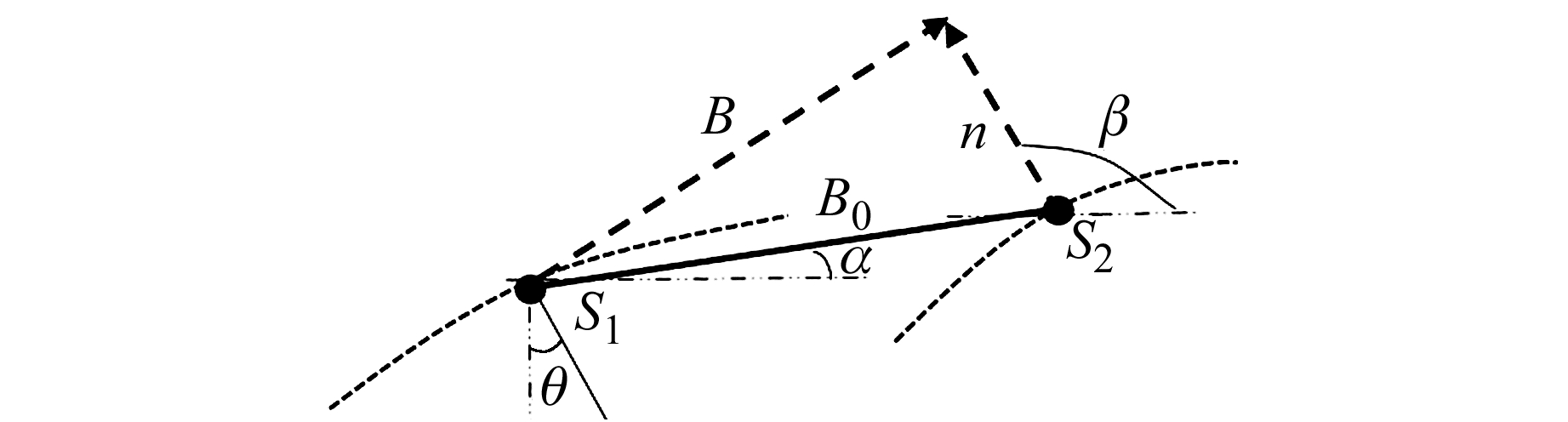
|
图 2 基线误差 Fig. 2 The baseline error |
由式(1)可将轨道误差对形变值的影响表示为:
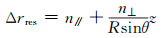
|
(5) |
假定轨道1和2的轨道误差是不相关且相等的,σacrosstrack与σradial分别为交轨和径向方向的标准差,则:

|
(6) |
由以上各式可得轨道误差对形变值影响的方差为:
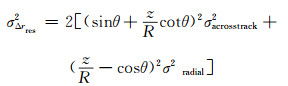
|
(7) |
上式即表达了交轨方向和径向误差与LOS向形变值方差的关系。但是,在实际应用中要完全去除轨道误差引起的相位,需要精密的定轨数据,即要求轨道绝对精度高于1 mm,目前的定轨精度还难以满足要求[8]。
2 联合GPS数据去除轨道误差由于InSAR获得的形变量是地表真实形变在卫星视线向的投影,为了估计干涉结果中轨道误差的影响,首先将GPS在N、E、U方向的三维位移转换到LOS方向上。转换公式如下:
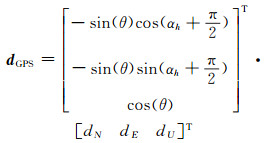
|
(8) |
式中,dGPS为GPS三维位移投影在LOS方向的位移量; dn、de、du分别为GPS三维位移矢量在南北、东西、垂直向的位移分量; αh为雷达的飞行方向; θ为雷达的侧视角。
将GPS三维位移转至LOS向时,θ一般取影像中心像元处的雷达侧视角,但实际上雷达影像上的侧视角是由近地点到远地点逐像元变化的,尤其是影像跨度大的时候,侧视角变化幅度也会很大。如本文采用的ALOS PALSAR标准数据,各条带内侧视角变化幅度约为5°。因此本文会考虑每个像元处雷达侧视角不同这一因素。
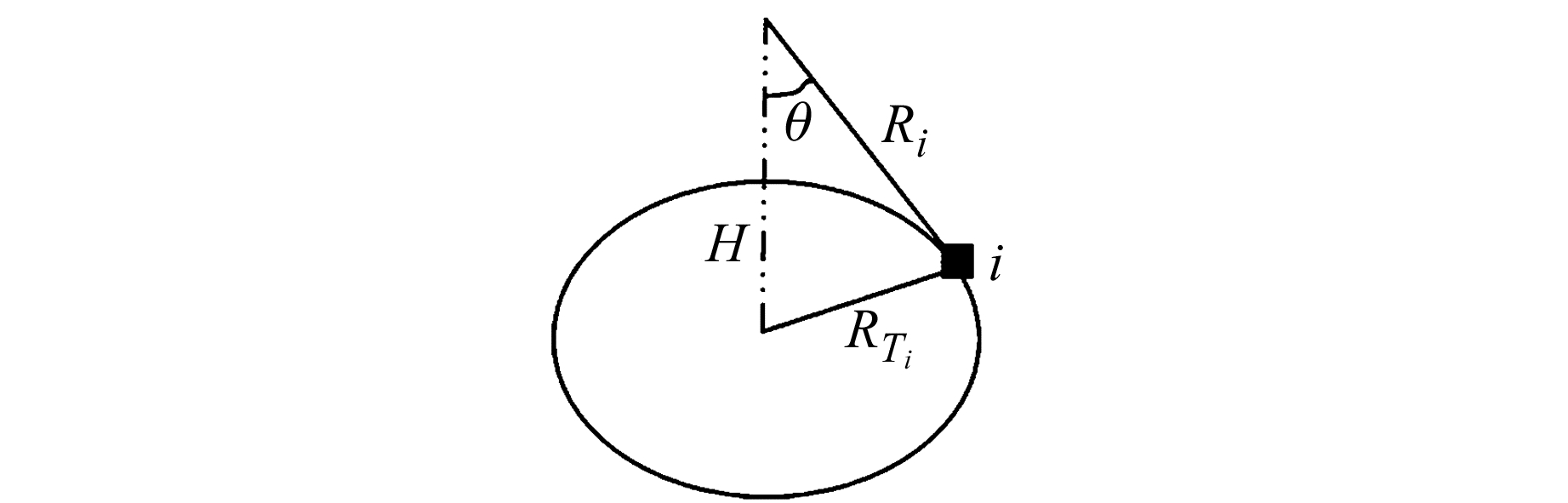
如图 3所示,对于距离向坐标为i的某像素,Ri表示该像素对应的雷达波入射斜距;RTi表示该位置处的地球曲率半径,其计算公式如下:
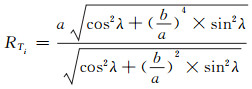
|
(9) |

|
(10) |
|
图 3 像元雷达侧视角 Fig. 3 The incident angle of any pixel |
式中,a、b分别为参考椭球的长、短半轴; λ取该像素的地理纬度; Δ为距离向的像素间距。通过余弦定理便可得到雷达侧视角的表达式:
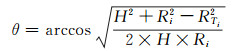
|
(11) |
式中,H为卫星到地心的距离。
假设共n个GPS测站,首先通过坐标转换得到每个点在干涉图中对应的像元位置, 然后利用InSAR观测值与GPS观测值拟合轨道误差dorbit,则像素i的轨道误差观测值表示为:
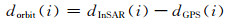
|
(12) |
利用一个二次曲面模型拟合轨道误差,拟合模型如下:
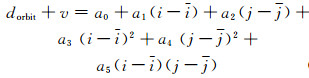
|
(13) |
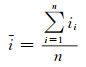
|
(14) |
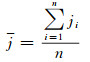
|
(15) |
式中,v为改正数,包括大气延迟误差、地形误差、余震形变等; (i,j)表示干涉图中像素坐标; a0、a1、a2、a3、a4和a5为拟合模型参数。矩阵形式为:
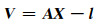
|
(16) |
式中,

|
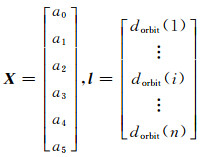
|
各像元的相干值γ介于0到1之间,相干值越大,权重也越大。若单位权中误差为σ0,则σi= 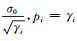

|
(17) |
模型参数的最小二乘解为:
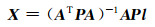
|
(18) |
单位权中误差估计值为:
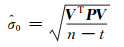
|
(19) |
取3倍中误差作为容许误差,将超出容许误差以及相干系数低于0.35的GPS点剔除,迭代求解模型参数。求得轨道误差拟合模型后,即可由像素坐标得到形变场内每个像元的轨道误差。对解缠后的干涉结果进行轨道误差改正,得到改正后的InSAR观测结果dcorrection:
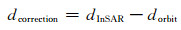
|
(20) |
通过改正后的结果与GPS在LOS向的形变值作差,得到改正后的干涉残差值,据此来评定轨道误差改正的精度。
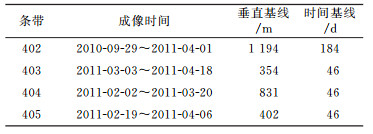
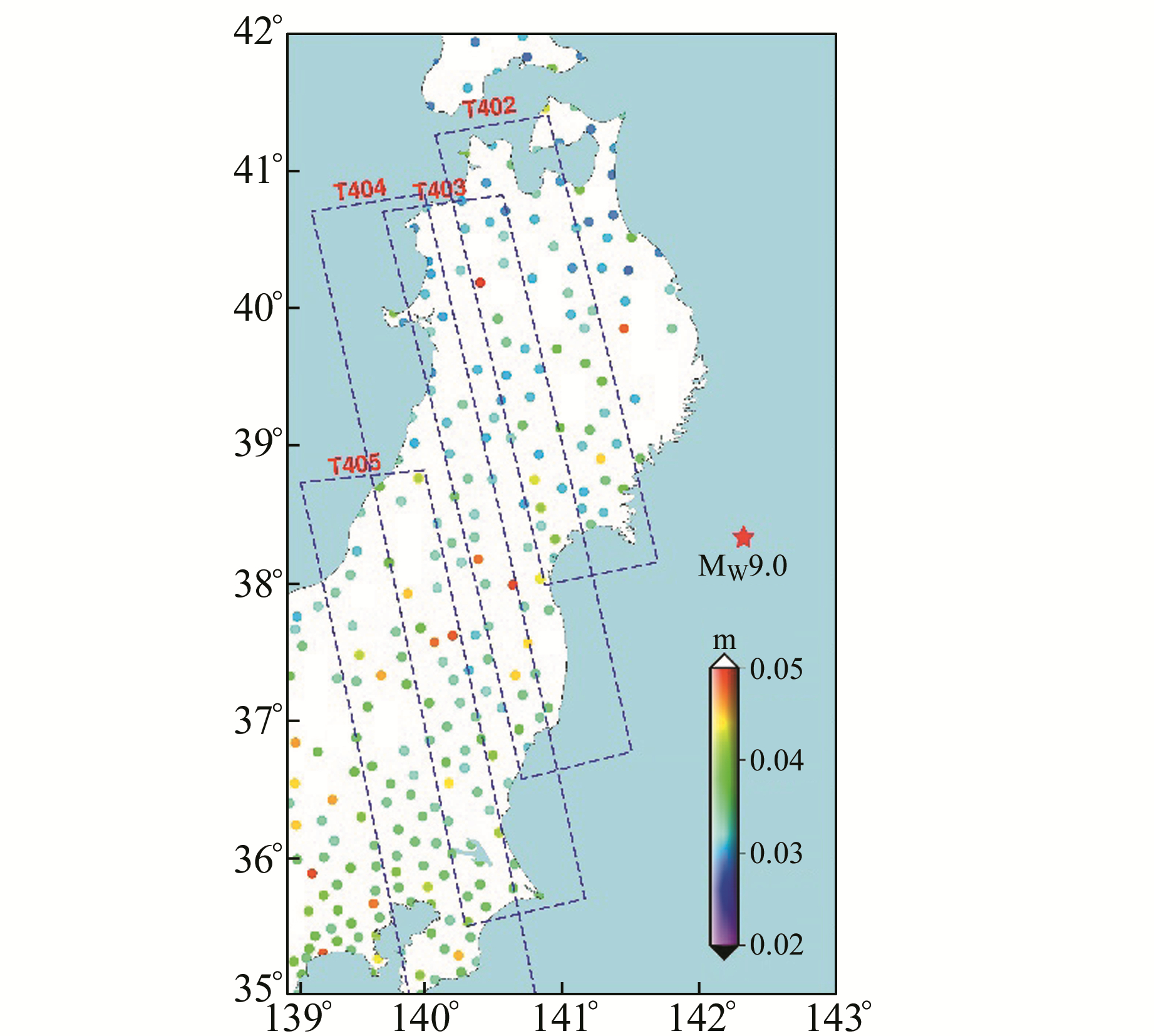
3 算例分析本研究采用ALOS卫星获取的Tohoku地震前后L波段的PALSAR升轨数据,数据格式是1.0的标准产品。共4个条带,编号分别为T402~T405,详细信息见表 1。采用的GPS数据是ARIA团队提供的共1 223个测站的同震位移解算结果[9],数据时间为2011-03-11 05:55~14:00(UTC)[9]。GPS测站分布及其点位中误差见图 4。其中,76%的GPS测站点位精度高于4 cm。数据处理中所采用的DEM是NASA提供的30 m分辨率的DEM数据。
|
|
表 1 雷达干涉像对 Tab. 1 Interferometric pairs used in this study |
|
图 4 GPS测站分布及其精度 Fig. 4 The distribution of GPS data and its precision 红色五角星表示震中,虚线框表示PALSAR升轨数据覆盖范围(T402~T405),圆点表示GPS测站,颜色表示点位中误差 |
InSAR数据处理平台为GAMMA软件。首先利用MSP模块进行成像处理,得到SLC。T402与T404条带的震后影像数据是FBD模式,而其余数据是FBS模式,因此成像后应先将T402与T404的SLC辅影像在距离向上进行降采样,使各条带主辅影像分辨率保持一致[10]。然后逐条带进行干涉数据处理和轨道误差的去除。步骤如下:
1) 进行差分干涉处理。本文采用二通法得到LOS向的InSAR同震形变场。为了获取较高的信噪比,在干涉处理过程中对PALSAR数据在距离向和方位向上分别进行多视处理。T403和T405条带的多视比取9:24,多视后强度图分辨率为67.47 m×75.50 m;T402与T404条带的多视比为9:48,强度图分辨率为133.81 m×151.13 m。干涉处理后得到差分干涉图见图 5(a),每个条纹代表着LOS向上11.8 cm的形变值。LOS向上形变相位误差主要由地形相位误差、电离层扰动、大气延迟等引起。由文献[6]可知,对于本次地震,地形相位误差与大气延迟误差均小于5 cm,与形变量级相比可以忽略不计;SAR数据中的电离层误差的影响经由文献[11]的方法检验后也可忽略不计,即轨道误差的影响占主要成分。因此可以得到结论:图 5(a)中条带间拼接处明显的不连续主要由轨道误差引起[6]。

|
图 5 同震形变干涉结果 Fig. 5 Coseismic deformation 红色方框表示余震 |
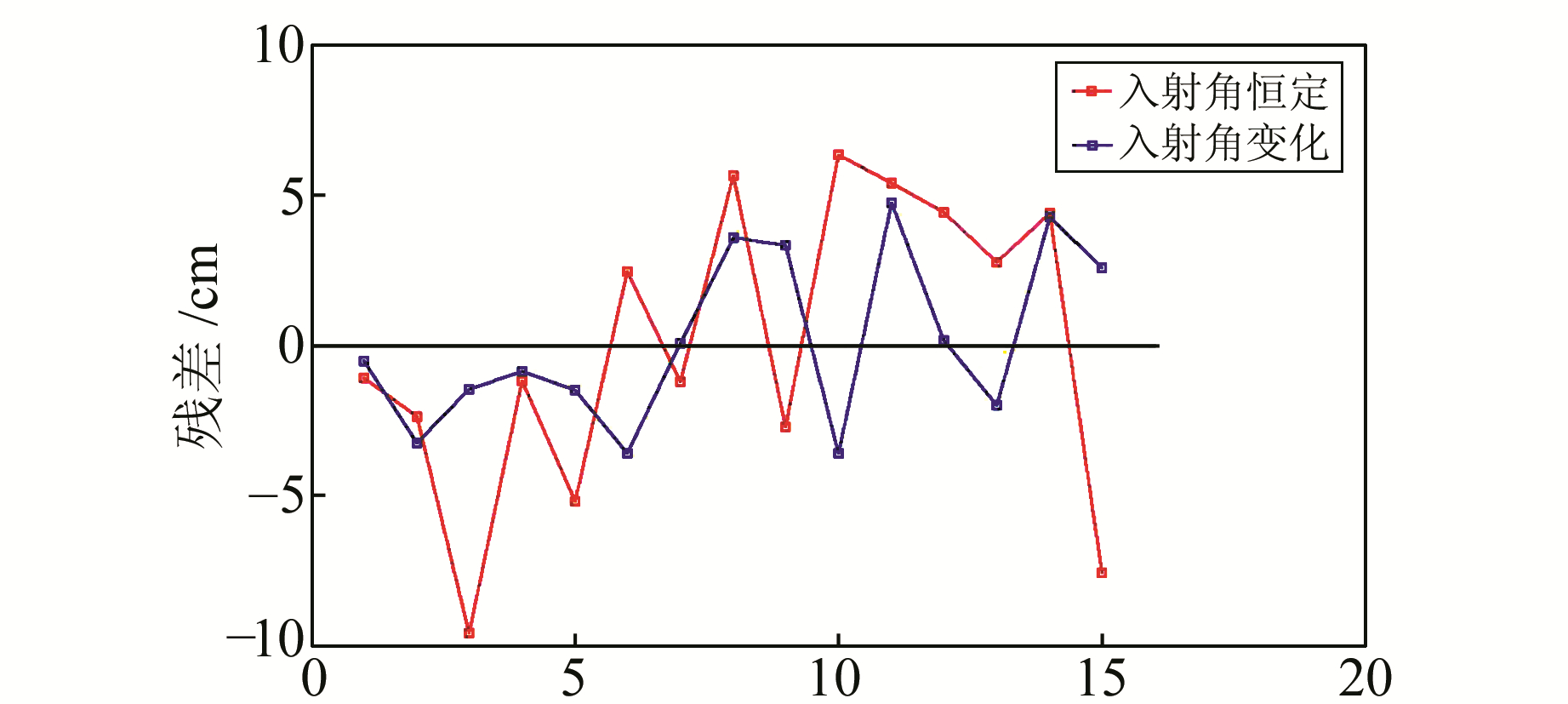
2) 将GPS测站的三维形变转至LOS向,并利用式(13)拟合一个二次曲面,即轨道误差拟合模型。其中,剔除相干系数值(图 5)低于0.35或者拟合残差超出3倍中误差的GPS测站。如图 6所示,最终筛选出的GPS测站共102个,点位精度均高于4 cm。选出15个均匀分布的测站来检核轨道误差改正后的精度,并且不参与轨道误差模型参数的求解。

|
图 6 相干系数和筛选后的GPS测站分布 Fig. 6 The coherence coefficient and the filtered GPS stations 参与模型解算的GPS测站由蓝色圆点表示,黑色三角形表示检核模型精度的GPS测站 |
利用其余87个测站进行轨道误差模型参数解算。各个条带进行二次曲面拟合时,线性部分的系数和二次项的系数比值均大于10-6,同时证明轨道误差有较强的二次曲面趋势[7]。将步骤1)中得到的InSAR同震形变场减去拟合出的轨道误差值即得到去除轨道误差后的LOS向的同震形变场。其中,GPS三维形变转换至LOS向时,若统一取中心像元处入射角38.7°进行计算,则LOS向方向矢量为(-0.1, -0.62,0.78)(分别对应N、E、U方向)。GPS三维方向至LOS向转换时仅取影像中心像元处的入射角,即视入射角恒定时得到的最终干涉结果为图 5(b);取GPS点所在像元处的入射角,即顾及入射角变化时得到的结果为图 5(c)。由图 6可见,轨道误差校正后,条带间拼接处条纹连续性明显提高,尤其是顾及GPS点对应像元处的入射角变化时,得到的条纹连续性更好。
图 7中同震位移呈现出以震中为中心的圆弧状,表明本次地震同震形变在LOS向的变化随着离震中距离由近到远,形变量由大到小,与实际情况基本一致。此外,由于SAR成像时间与GPS观测时间差别较大以及GPS观测值在垂直向的精度较低和InSAR结果中大气延迟误差等的影响,InSAR形变场结果与GPS观测结果相比,包含一定的震前构造形变、震后构造运动、非构造运动及震后蠕变等,特别是在近震区的影响会更大。所以这会造成两类观测值之间在除去轨道误差之后仍存在一定的差异。地势平坦地区相干性较高,冰雪和植被覆盖、地形误差或者垂直基线太长等均会导致相干性较低,从而也会影响解缠结果。由图 7可知,403与404条带拼接处的南部有一小块形变值较大的区域(图 7红框内),对应图 4中红框内的条纹密集区域,结合实际地震情况可知,这主要是由于当地发生了7.9级的余震所致。

|
图 7 LOS向同震位移场 Fig. 7 Coseismic deformation in the direction of LOS |
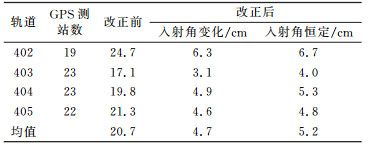
为了定量评价轨道误差改正后的InSAR同震形变场精度,由各个条带内参与轨道误差模型解算的GPS测站(共87个)在LOS向的形变与轨道误差改正前、后的InSAR形变值作差,得到每个条带改正前、后的残差RMS值(表 2)。改正前的残差RMS均值为20.7 cm,轨道误差改正后为4.7 cm(视入射角变化时),可见改正后的形变值与GPS形变值的偏差明显变小。顾及入射角变化时,各条带RMS值分别为6.3 cm、3.1 cm、4.9 cm、4.6 cm,与入射角恒定时的RMS值6.7 cm、4.0 cm、5.3 cm、4.8 cm相比,结果改善更为明显。其中402和404条带的RMS值较大,可能与其垂直基线较长有关。同时,在每一个条带内选取一部分没有参与轨道误差模型解算的GPS点(共15个)作精度检验,利用改正后的InSAR形变值与LOS向的GPS形变作差得到残差值(图 8)。考虑入射角变化比入射角恒定时的改正后残差值更为稳定,变化曲线更为平缓,变化范围均在-10~10 cm内。因此,在利用GPS观测结果作轨道误差改正时,考虑像元入射角变化得到的同震形变结果更为准确。由校正后的同震位移场可知,LOS向的形变值在402条带的南部区域(即靠近震中区域)达到最大,这与GPS形变场一致。
|
|
表 2 各条带轨道误差改正前后的RMS值 Tab. 2 RMS of InSAR results before and after orbital ramps correction |
|
图 8 15个GPS测站校正后的残差对比 Fig. 8 The residuals of fifteen GPS stations |
对于长条带大范围的InSAR数据,轨道误差对同震干涉形变有着重要的影响。本文利用2011年日本Tohoku MW9.0大地震的61景PALSAR数据获取了该地震4个条带的同震形变干涉结果,并通过GPS的三维位移场校正InSAR干涉结果中的轨道误差,校正后结果得到明显改善,验证了考虑雷达影像入射角变化时校正结果的稳定性更高。同时,分析改正后的差分形变干涉图可以发现,InSAR技术能够监测到GPS网难以监测到的余震变形。联合GPS和InSAR的形变监测,为深入研究该次地震的动力学机制提供了高精度、高空间分辨率的观测数据。
| [1] |
陈强, 刘国祥, 胡植庆, 等. GPS与PS-InSAR联网监测的台湾屏东地区三维地表形变场[J]. 地球物理学报, 2012, 55(10): 3248-3258 (Chen Qiang, Liu Guoxiang, Hu Zhiqing, et al. Mapping Ground 3-D Displacement with GPS and PS-InSAR Networking in the Pingtung Area, Southwestern Taiwan, China[J]. Chinese Journal of Geophysics, 2012, 55(10): 3248-3258 DOI:10.6038/j.issn.0001-5733.2012.10.007)
(  0) 0) |
| [2] |
杨少敏, 聂兆生, 贾志革, 等. GPS解算的日本MW9.0地震的远场同震地表位移[J]. 武汉大学学报:信息科学版, 2011, 36(11): 1336-1339 (Yang Shaomin, Nie Zhaosheng, Jia Zhige, et al. Far-field Coseismic Surface Displacement Caused by the MW9.0 Tohoku Earthquake[J]. Geomatics and Information Science of Wuhan University, 2011, 36(11): 1336-1339)
(  0) 0) |
| [3] |
荆燕, 王建军, 张景发, 等. D-InSAR技术在地震同震形变研究中的应用[J]. 测绘科学, 2004, 29(2): 64-69 (Jing Yan, Wang Jianjun, Zhang Jingfa, et al. The Co-Seismic Deformation Research Using D-InSAR Observation[J]. Science of Surveying and Mapping, 2004, 29(2): 64-69 DOI:10.3771/j.issn.1009-2307.2004.02.021)
(  0) 0) |
| [4] |
徐克科, 牛元甫, 伍吉仓, 等. 联合GPS、InSAR建立同震地表三维位移[J]. 大地测量与地球动力学, 2014, 34(1): 15-18 (Xu Keke, Niu Yuanfu, Wu Jicang, et al. Establishment of 3D Coseismic Terrain Displacement Field with GPS and InSAR[J]. Journal of Geodesy and Geodynamics, 2014, 34(1): 15-18)
(  0) 0) |
| [5] |
许才军, 何平, 温扬茂, 等. 日本Tohoku-Oki MW9.0地震的同震形变及其滑动分布反演:GPS和InSAR约束[J]. 武汉大学学报:信息科学版, 2012, 37(12): 1387-1391 (Xu Caijun, He Ping, Wen Yangmao, et al. Coseismic Deformation and Slip Distribution for 2011 Tohoku-Oki MW 9.0 Earthquake: Constrained by GPS and InSAR[J]. Geomatics and Information Science of Wuhan University, 2012, 37(12): 1387-1391)
(  0) 0) |
| [6] |
Feng G C, Ding X L, Li Z W, et al. Calibration of an InSAR-Derived Coseimic Deformation Map Associated With the 2011 MW9.0 Tohoku-Oki Earthquake[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(2): 302-306 DOI:10.1109/LGRS.2011.2168191
(  0) 0) |
| [7] |
杨红磊, 彭军还, 张丁轩, 等. 轨道误差对InSAR数据处理的影响[J]. 测绘科学学报, 2012, 29(2): 118-126 (Yang Honglei, Peng Junhuan, Zhang Dingxuan, et al. Influence of Orbital Errors on InSAR Data Processing[J]. Journal of Geomatics Science and Technology, 2012, 29(2): 118-126)
(  0) 0) |
| [8] |
龙四春, 李陶. D-InSAR中参考DEM误差与轨道误差对相位贡献的灵敏度研究[J]. 遥感信息, 2009(2): 3-6 (Long Sichun, Li Tao. Phase Sensitivity Study on D-InSAR for Reference DEM and Orbit Error[J]. Remote Sensing Information, 2009(2): 3-6 DOI:10.3969/j.issn.1000-3177.2009.02.001)
(  0) 0) |
| [9] |
ARIA. ARIA GPS Displacement Data Provided by JPL and Caltech [EB/OL]. ftp://sideshow.jpl.nasa.gov/pub/usrs/ARIA/,2011
(  0) 0) |
| [10] |
许才军, 林敦灵, 温扬茂. 利用InSAR数据的汶川地震形变场提取及分析[J]. 武汉大学学报:信息科学版, 2010, 35(10): 1138-1142 (Xu Caijun, Lin Dunling, Wen Yangmao. Extract and Analysis Surface Deformation Caused by Wenchuan MW7.9 Earthquake from InSAR Data[J]. Geomatics and Information Science of Wuhan University, 2010, 35(10): 1138-1142)
(  0) 0) |
| [11] |
Wegmuller U, Werner C L, Srozzi T, et al. Ionospheric Electron Concentration Effects on SAR and InSAR[C]. IGARSS, Denver, 2006
(  0) 0) |
2. Shanghai Astronomical Observatory, CAS, 80 Nandan Road, Shanghai 200030, China
 2017, Vol. 37
2017, Vol. 37