2. 流域生态与地理环境监测国家测绘地理信息局重点实验室, 南昌市广兰大道418号, 330013;
3. 江西省水利规划设计院, 南昌市北京东路1038号, 330029
传统GM(1, 1)模型固有的系统误差会给预测工作造成一定的负面影响,针对传统GM(1, 1)模型的背景值取紧邻均值的不足,周世健等[1]、李大军等[2]提出了加权的PGM(1, 1)模型;牛东晓等[3]针对不同变化趋势的背景值取相同的参数值不能充分降低模型的预测误差,引入不同的参数pi(i=1, 2, …, n-1)来改进GM(1, 1)模型背景值序列的计算公式,在不同的时刻对应不同的pi(i=1, 2, …, n-1);王忠桃[4]、王宝强等[5]将这种背景值构造方法和灰元N引入GM(1, 1)的预测模型建立了灰色非线性模型,弱化了累加序列须成某一指数变化规律,提高了拟合精度。但以上研究都只顾及了背景值而忽略初始值对预测模型精度的影响。本文通过分析GM(1, 1)和PGM(1, 1)的不足,在对初始值进行改正的同时引入王忠桃、王宝强等人提出的背景值构造方法和灰元N建立综合优化的灰色非线性模型,顾及引入的未知参数较多,用传统方法难以求解,而粒子群算法适用多目标优化且具有收敛速度快、结构简单的特点,故采用粒子群算法求解最优参数,从而建立基于粒子群算法和加权灰色组合的PSO-GM模型。通过两个实例对比分析,验证了优化模型的可靠性和实用性。
1 GM(1, 1)缺陷分析和PGM(1, 1)的建模机理 1.1 GM(1, 1)缺陷分析由灰色模型的建模过程可知,传统GM(1, 1)模型背景值构造公式如下:
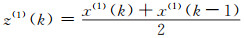
|
(1) |
其中x(1)(k)=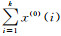
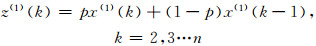
|
(2) |
由公式推导可得p和a存在如下关系:
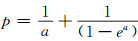
|
(3) |
可证明,当|a|趋向0时,p趋向于0.5;当|a|较小时,p非常接近0.5;当|a|较大时,p与0.5偏离较大。因此,简单地取p等于0.5是导致传统GM(1, 1)模型|a|较大时预测失效的原因。
1.2 PGM(1,1)模型的建立针对上述问题,利用式(2)的背景值取值方法建立PGM(1, 1)模型。具体算法为:p的确定是先取p=0.5作为近似值,以原始序列和模拟序列的平均相对误差最小为约束条件,按传统GM(1,1)模型建立方法,得到灰参数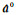
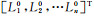
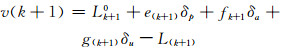
|
(4) |
组成矩阵形式为:
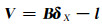
|
(5) |
其中,V=[v(2), v(3), …, v(n)]T; δX=[δp, δa, δu]; l=[l(2), l(3), …, l(n)]; l(k+1)=L(k+1)-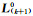
文献[3]针对不同变化趋势的背景值取相同的参数值不能充分降低模型的预测误差,引入不同的参数pi(i=1, 2, …, n-1)来改进GM(1, 1)模型背景值序列的计算公式,在不同时刻对应不同pi(i=1, 2, …, n-1)。文献[4]将这种背景值构造方法和灰元N同时引入GM(1, 1)的预测模型,建立了灰色非线性模型。本文在这些基础上通过引入初始值改正和上面提到的背景值构造方法及灰元N,建立优化的灰色非线性模型,命名为GM(1, 1, N, p, ξ)模型。其中ξ(任意值)为x(0)(1)=x(0)(1)+ξ的修正值,并以此作为四阶龙格-库塔法求解累加序列的初始值。
2.1 PSO-GM(1, 1, N, p, ξ)建模机理设有非负序列X0=(x0(1), x0(2), …, x0(n)),对该序列进行一次累加X(1)=(x(1)(1), x(1)(2), …, x(1)(n)),其中x(1)(k)=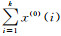
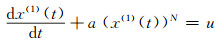
|
(6) |
上式也可以表示为:
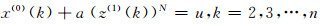
|
(7) |
灰参数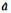
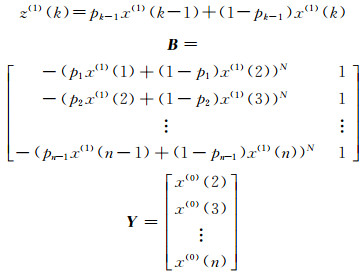
|
求出灰参数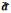
由于引入的参数较多,一般的方法难以求解,而粒子群算法对求解非线性、不可微的复杂优化问题收敛速度快、解质量高,并且粒子群算法程序实现简单,适合多目标优化问题求解。具体算法可描述为:设搜索区域为D维空间,种群中共有M个粒子,粒子i在第t次迭代的位置为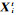
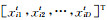
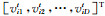

|
(8) |
为使得粒子的速度在更新时不至过大,设置v∈(-2, 2)。公式的第一部分为粒子先前的速度;第二部分表示粒子自身的经验和记忆;第三部分表示粒子间信息共享与相互合作。式中,t为当前迭代次数;c1为粒子更新自身最优值的学习因子,c2为粒子更新全部粒子最优值的学习因子,c1、c2一般取值为2;r1和r2为[0, 1]区间的随机数;ω为惯性权重,它是保持原来速度大小的因子。ω较大时有利于跳出局部最优解,进行全局搜索;ω较小时有利于局部寻优,加快算法收敛。文中采用随迭代次数线性递减的ω值:
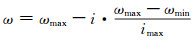
|
(9) |
式中,ωmax=0.95, ωmin=0.4,i为当前迭代次数,imax为最大迭代次数。
适应度函数为:
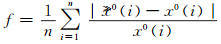
|
(10) |
具体算法流程:
1) 初始化粒子群,包括种群规模m=30,粒子维数为n,最大迭代次数imax=1 000,粒子位置yi=[λi1, λi2…λin-1, Ni, ξi]和速度Vi=[vi, 1, vi, 2, …, vi, n, vi, n+1],其中0.1≤λi≤1, N∈(0, 2)。根据适应度函数计算每个粒子的适应度[3]。
2) 根据全部粒子适应度大小初始化个体极值Pi和计算全局极值Pg。
3) 迭代寻优,由式(9)更新惯性权重,由式(8)更新每个粒子的速度和位置,并限制其速度满足v∈(-2, 2),计算每个粒子的适应度fi,并和个体极值比较。若fi < f(Pi),则将fi替换为当前粒子的最佳值,f(Pi)=fi,同时更新当前粒子的最优位置Pi=yi。
4) 将每个粒子的当前最优值和全局最优值比较,若f(Pi) < f(Pg),则将f(Pi)替换为当前全局最优值,即f(Pg)=f(Pi),同时更新全局最优位置。
5) 判断迭代次数是否达到最大迭代值,若是则输出全局极值和全局最优位置,以及计算出对应的模拟和预测序列。否则转入第2步,直至满足迭代条件。
2.2 优化模型的精度检验优化模型的精度评定主要从3个方面着手:1)计算均方差比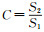
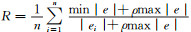
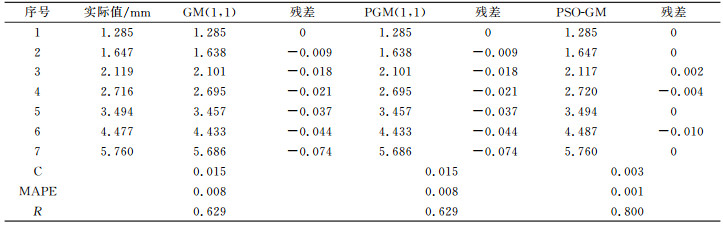
以某大坝边坡变形监测线上的一观测点设为A点的位移值(数据取自文献[10]),取前7期分别用GM(1, 1)、PGM(1, 1)、PSO-GM(1, 1, N, p, ξ)建立模型,PSD-GM得到的最优参数y=[0.363, 0.100, 1.000, 0.168, 0.100, 0.823, 0.997, 0.210],具体数据对比分析见表 1、表 2。
|
|
表 1 实测值与模拟值对比分析(实例1) Tab. 1 Comparative analysis of measured and simulated values(example 1) |
|
|
表 2 实测值与预测值对比分析(实例1) Tab. 2 Comparison of measured and predicted values(example 1) |
表 1、表 2中各模型拟合和预测结果表明,PGM(1, 1)模型和GM(1, 1)模型模拟与预测精度一致,说明当序列呈一定单调性变化时,使得PGM(1, 1)最优的p刚好为0.5,PGM(1, 1)便还原为GM(1, 1),而PSD-GM通过粒子群算法优化参数,使得模型的模拟和预测精度在3种模型中最高。PSD-GM得到的灰色关联度R=0.8,而GM(1, 1)和PGM(1, 1)的灰色关联度R=0.629,R越大说明拟合值序列越好地保持了原始序列的内在变化规律,模型的模拟和预测效果越好。对比3种模型的精度评定结果表明,本文模型的均方差比仅为0.003,相对误差均值为0.000 67,而GM(1, 1)、PGM(1, 1)的均方差比和相对误差均值分别为0.015和0.008,相比减少了一个数量级。究其原因,是本文模型对初始值和背景值都进行了改进,相对传统模型和PGM(1, 1)模型精度都得到较大提高。
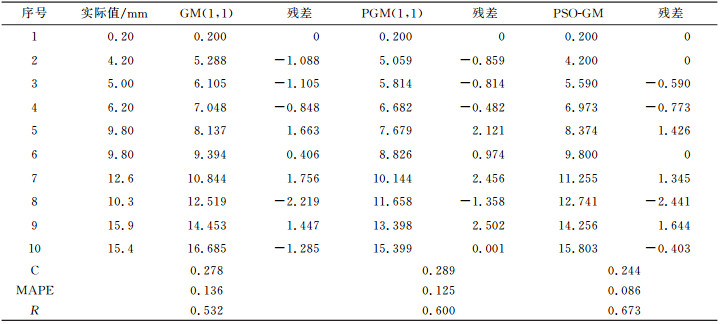
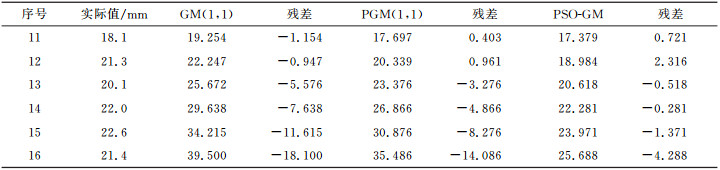
为了进一步说明模型的可靠性和适用性,引用文献[1]中实例,即湖北秭归县链子崖危岩体某监测点1978~1993年的监测资料。首先以1978~1987年实测值为原始数据序列,分别建立10维的GM(1, 1)、PGM(1, 1)和PSO-GM(1, 1, N, p, ξ),本文模型寻得的最优参数y=[0.100, 0.100, 0.100, 0.100, 0.100, 0.100, 1.000, 0.100, 0.100, 0.580, 2.520]。同时用这3种模型来预测1988~1993年变形值并与实测值比较,具体数据见表 3、表 4、图 1。
|
|
表 3 实测值与模拟值对比分析(实例2) Tab. 3 Comparative analysis of measured and simulated values(example 2) |
|
|
表 4 实测值与预测值对比分析(实例2) Tab. 4 Comparison of measured and predicted values(example 2) |
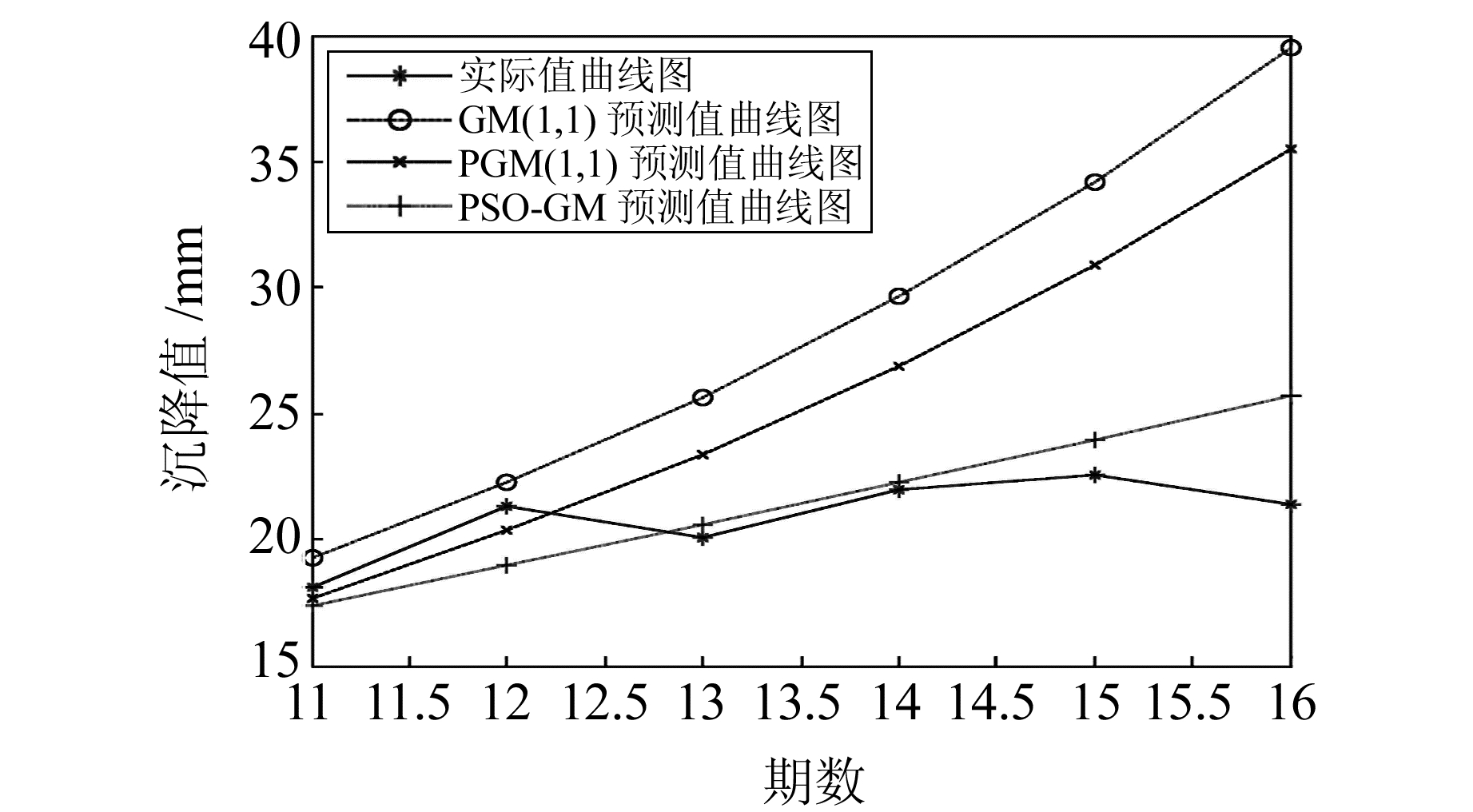
|
图 1 各模型预测值和实测值曲线(实例2) Fig. 1 The curves of predicted and practical data(example 2) |
表 3、表 4、图 1的结果显示,GM(1, 1)模型得到的均方差比为0.278,相对误差均值为0.136,灰色关联度为0.532;PGM(1, 1)模型得到的均方差比为0.289,相对误差均值为0.125,灰色关联度为0.6;PSD-GM的均方差比为0.244,相对误差均值为0.086,灰色关联度为0.673。说明PGM(1, 1)模型的预测精度总体略优于传统GM(1, 1)模型,验证了优化背景值能提高模型的模拟和预测精度。而PSD-GM模型得到的3种精度指标均优于PGM(1, 1)和GM(1, 1)模型,说明针对初始值和背景值同时改进的PSD-GM模型,既能更好地保存原始序列的内在变化规律,又进一步提高了模型的模拟和预测精度。从3种模型的预测结果对比分析看,随着预测时间的增长,3种模型的预测误差都大致呈递增趋势。通过3种模型的残差对比分析,随着预测区间的增大,除了前两期预测误差略大于PGM(1, 1)和GM(1, 1),其余残差均优于PGM(1, 1)和GM(1, 1)模型,个别甚至提高了一个数量级。两次实验结果表明,基于初始值和背景值改进的PSO-GM(1, 1, N, p, ξ)模型兼具有GM(1, 1)和PGM(1, 1)的特性,同时也克服了两种模型存在的缺陷,明显提高了前两种模型的预测精度。
4 结语本文基于初始值和背景值同时改进的灰色模型,通过引入不同背景权重p和灰指数N,并用改进的初始值由龙格-库塔法求解累加序列的模拟值和预测值,通过粒子群算法求解最优参数。优化模型克服了传统GM(1, 1)和PGM(1, 1)的不足,同时又兼具两种模型的特性,即当N=1, p1=p2=…=pn, ξ=0时即为PGM(1, 1)模型;当N=1,pi=0.5,ξ=0时即为GM(1, 1)模型。通过两个工程实例证明,优化模型的拟合精度高,预测效果好,预测周期长,能够很好地反映形变发生的内在规律,相比其他两种模型有更高的实用价值。
| [1] |
周世健, 赖志坤, 臧德彦, 等. 加权灰色预测模型及其计算实现[J]. 武汉大学学报:信息科学版, 2002, 27(5): 451-455 (Zhou Shijian, Lai Zhikun, Zang Deyan, et al. Weighted Grey Prediction Model and Implement of Its Compution[J]. Geomatics and Imformation Science of Wuhan University, 2002, 27(5): 451-455)
(  0) 0) |
| [2] |
李大军, 孙旭红, 汤拥军. PGM(1, 1)灰色预测模型及其应用[J]. 华东地质学院学报, 2002, 25(1): 40-43 (Li Dajun, Sun Xuhong, Tang Yongjun. PGM(1, 1) Grey Prediction Model and Its Application[J]. Journal of East China Geological Institute, 2002, 25(1): 40-43 DOI:10.3969/j.issn.1674-3504.2002.01.009)
(  0) 0) |
| [3] |
牛东晓, 赵磊, 张博, 等. 粒子群优化灰色模型在负荷预测中的应用[J]. 中国管理科学, 2007, 15(1): 69-73 (Niu Dongxiao, Zhao Lei, Zhang Bo, et al. The Application of Particle Swarm Optimization Based Grey Model to Power Load Forecasting[J]. Chinese Journal of Managenment Science, 2007, 15(1): 69-73 DOI:10.3321/j.issn:1003-207X.2007.01.013)
(  0) 0) |
| [4] |
王忠桃.灰色预测模型相关技术研究[D].成都: 西南交通大学, 2008 (Wang Zhongtao.Research on Technique of Grey Prediction Model[D].Chengdu: Southeast Jiaotong University, 2008) http://cdmd.cnki.com.cn/Article/CDMD-10613-2008177977.htm
(  0) 0) |
| [5] |
王宝强, 崔伟杰, 温毓繁, 等. PSO-GM模型在拱坝变形预报中的应用[J]. 三峡大学学报:自然科学版, 2014, 36(5): 23-27 (Wang Baoqiang, Cui Weijie, Wen Yufan, et al. Applic-ation of PSO-GM Model to Prediction of Arch Dam Deformation[J]. Journal of China Three Gorge University: Nature Science, 2014, 36(5): 23-27)
(  0) 0) |
| [6] |
李克昭, 李志伟, 孟福军, 等. 基于综合优化GM(1, 1)的形变预测模型[J]. 大地测量与地球动力学, 2016, 36(2): 120-123 (Li Kezhao, Li Zhiwei, Meng Fujun, et al. Deformation Forecasting Model Based on Synthetic and Optimized GM(1, 1)[J]. Journal of Geodesy and Geodynamics, 2016, 36(2): 120-123)
(  0) 0) |
| [7] |
王奉伟, 周世健, 周清, 等. 三重加权变形监测预测模型及应用[J]. 测绘科学, 2016, 41(4): 10-14 (Wang Fengwei, Zhou Shijian, Zhou Qing, et al. Application of Development Weighted Treble in TPGM(1, 1) Model[J]. Science of Surveying and Mapping, 2016, 41(4): 10-14)
(  0) 0) |
| [8] |
郭文杰.基于灰色系统理论的深基坑边坡稳定性研究[D].武汉: 华中科技大学, 2006 (Guo Wenjie.Study on Slope Stability of Deep Foundation Excavation Based on the Gray System Theory[D].Wuhan: Huazhong University of Science and Thchnology, 2006) http://cdmd.cnki.com.cn/Article/CDMD-10487-2008024317.htm
(  0) 0) |
| [9] |
王大鹏, 汪秉文. 基于变权缓冲灰色模型的中长期负荷预测[J]. 电网技术, 2013, 37(1): 167-171 (Wang Dapeng, Wang Bingwen. Medium and Long-Term Load Forecasting Based on Variable Weights Buffer Grey Model[J]. Power System Technology, 2013, 37(1): 167-171)
(  0) 0) |
| [10] |
赖志坤, 王新洲, 朱欣焰. PGM(1, 1)预测模型及其参数估计[J]. 测绘通报, 2003(11): 14-16 (Lai Zhikun, Wang Xinzhou, Zhu Xinyan. PGM(1, 1) Forecasting Model and Its Parameter Estimate[J]. Bulletin of Surveying and Mapping, 2003(11): 14-16 DOI:10.3969/j.issn.0494-0911.2003.11.006)
(  0) 0) |
| [11] |
李夏云, 陈传淼. 用龙格-库塔法求解非线性方程组[J]. 数学理论与应用, 2008(2): 62-65 (Li Xiayun, Chen Chuanmiao. Solving Nonliner Equations by Using Runge-Kutta Method[J]. Mathematical Theory and Applications, 2008(2): 62-65)
(  0) 0) |
2. Key Laboratory of Watershed Ecology and Geographical Environment Monitoring, NASMG, 418 Guanglan Road, Nanchang 310013, China;
3. Water Conservancy Planning and Designing Institute of Jiangxi Province, 1038 East-Beijing Road, Nanchang 330029, China
 2017, Vol. 37
2017, Vol. 37