GM(1, 1)模型自提出以来便一直受其固有缺陷的困扰,即不具备白指数率预测无偏性。后经各种各样的改进和拓展,GM(1, 1)模型的预测精度和应用范围得到了提高和扩展,在变形监测领域也得到了广泛的应用[1-4]。但在实际工程中,受各种因素的影响,变形监测数据往往具有非等时间间隔的性质,这种情况下GM(1, 1)模型便不能直接应用。为了拓展GM(1, 1)模型的应用范围,一些学者提出了非等距GM(1, 1)模型,可用于非等距数据序列的建模分析。加权非等距GM(1, 1)模型最先提出[5-6],后在其基础上提出了灰线性加权非等距GM(1, 1)模型[7]。笔者也提出了一种用于建筑物沉降分析预测的非等距GM(1, 1)模型[8]。3种非等距GM(1, 1)模型的建模原理不尽相同,其应用效果自然也不相同。为了选择合理有效的非等距GM(1, 1)模型,本文结合理论和实例分析,对上述3种非等距GM(1, 1)模型在沉降预测中的应用效果进行探讨。
1 加权与线性加权非等距GM(1, 1)模型分析 1.1 加权非等距GM(1, 1)模型分析加权非等距GM(1, 1)模型是以时间间隔作为权重对非等距数据进行加权累加,再按照GM(1, 1)模型的建模步骤求解模型参数。模型预测式如下[5-6]:
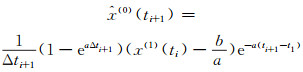
|
(1) |
式中,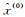
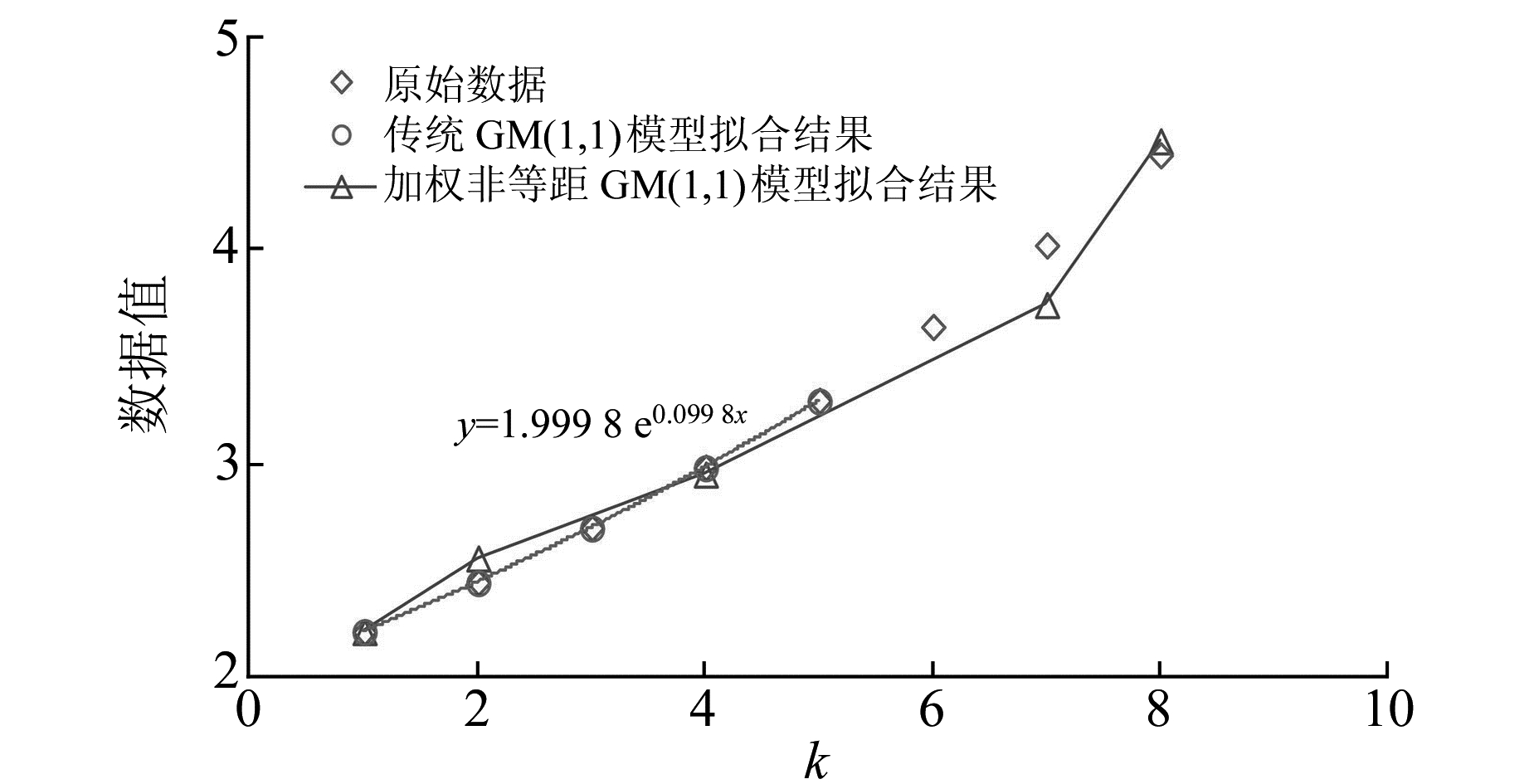
从式(1)可以看出,受时间间隔非等距的影响,加权非等距GM(1, 1)模型拟合结果不再是指数序列,而是不规则序列[8]。这样就产生了矛盾,比如对于指数序列2e0.1k,取k=1,2,3,4,5是一组等距数据,取k=1,2,4,7,8是一组非等距数据。分别建立传统GM(1, 1)模型和加权非等距GM(1, 1)模型,拟合结果见图 1。从图 1可以看出,传统GM(1, 1)模型拟合效果很好,拟合函数为1.999 8 e0.099 8 k,微小误差是由GM(1, 1)模型的固有缺陷导致的。而加权非等距GM(1, 1)模型的拟合结果与原始数据存在较大误差,并且不再是指数序列,这与GM(1, 1)模型相违背。对于具有近似指数趋势的沉降数据,并不适用于加权非等距GM(1, 1)模型。
|
图 1 传统GM(1, 1)模型和加权非等距GM(1, 1)模型拟合结果对比 Fig. 1 Comparison of the fitting results between existing GM(1, 1) model and weighted non-equidistance GM(1, 1) model |
文献[7]在加权非等距GM(1, 1)模型的基础上建立了灰线性加权非等距GM(1, 1)模型,但详细分析其建模过程可以看出,其并非真正的非等距模型。参考文献[7],灰线性加权非等距GM(1, 1)模型的建模过程可以概述如下。
1) 对原始非等时距数据序列X(0)进行加权累加,建立加权非等距GM(1, 1)模型,并获得拟合值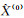
2) 将加权非等距GM(1, 1)模型所得拟合值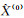
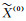
在不讨论加权非等距GM(1, 1)模型是否合理的情况下,从上述建模过程可以发现存在如下问题:
1) 既然要采用灰色线性回归组合模型,为何不用原始数据序列X(0),而用其拟合值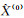
2) 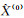
上述分析指出了灰线性加权非等距GM(1, 1)模型存在的问题,但是该模型在文献[7]中的实例计算中获得了较高的拟合和预测精度,这其实是一种巧合。下面对此进行分析。
文献[7]中选择文献[9]中居民楼1栋CJ1沉降点的沉降累计观测数据为例,利用前8期沉降数据构建灰线性加权非等距GM(1, 1)模型,预测第9~13期的沉降数据,具体数据和结果参见文献[7]。
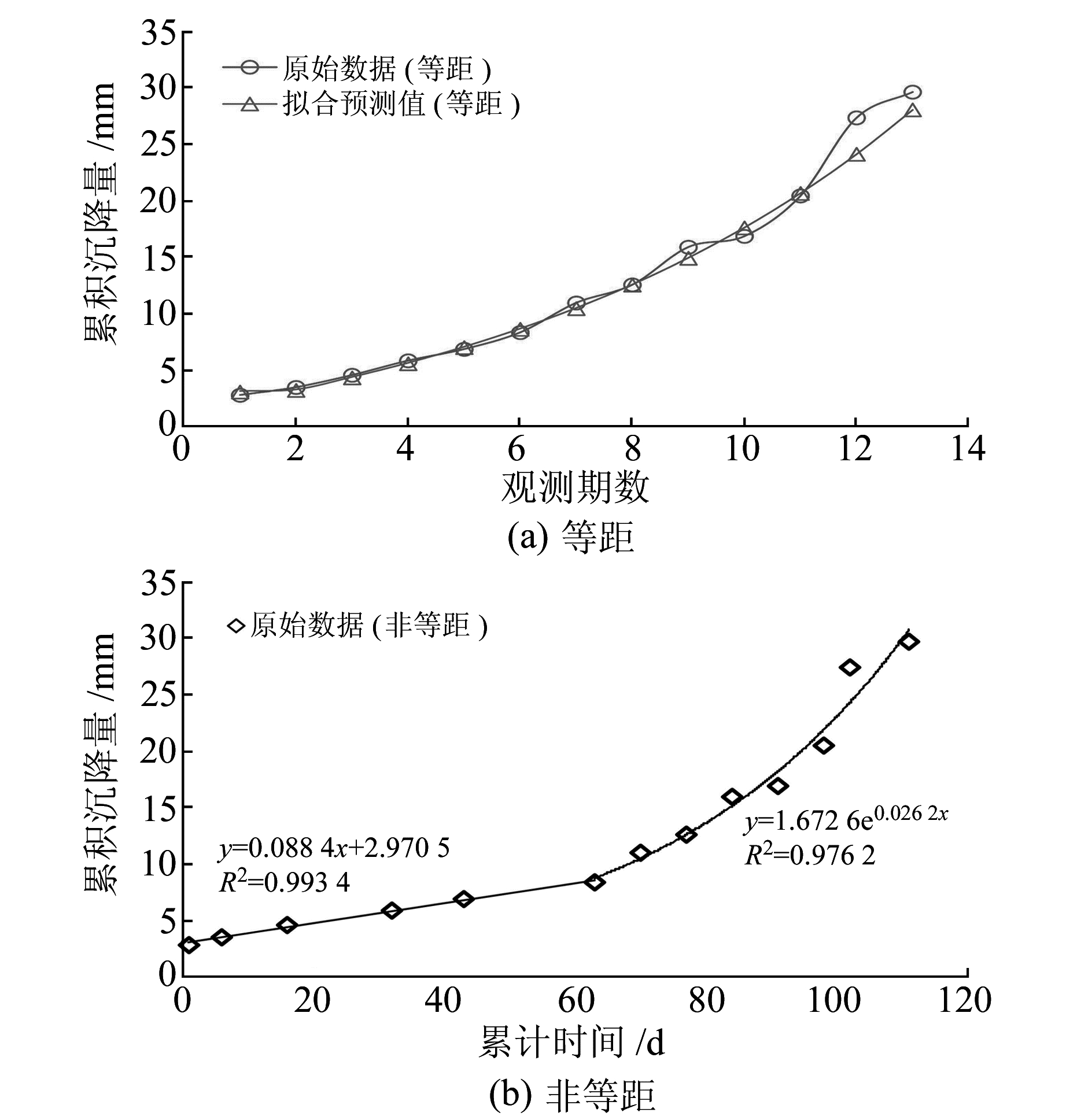
从文献[7]的结果可以看出,灰线性加权非等距GM(1, 1)模型的拟合和预测效果都比较好,这是忽略非等时间间隔而导致的巧合结果。图 2给出了考虑非等时间间隔的真实沉降发展趋势。从图 2(b)可以看出,初始阶段的沉降具有线性发展趋势,随后增长速度加快,具有指数发展趋势。对于这种沉降变化趋势,可在其进入快速增长阶段时,利用指数模型进行分析预测。如果不考虑时间间隔,视为等距数据序列,则从图 2(a)可以看出,此时沉降发展趋势发生变化,整体上更接近于指数发展趋势,此时灰线性加权非等距GM(1, 1)模型正好可用于此种数据,所以得到了较好的拟合和预测效果。对于随后的第14期数据,灰线性加权非等距GM(1, 1)模型可以得到一个预测值,但是该预测值对应的时间点是什么,时间间隔如何选择,该模型未给出解释,并且也无法解决这个问题。
|
图 2 等距与非等距沉降变化趋势 Fig. 2 The observation accumulative subsidence of non-equidistance interval and equidistance interval |
除上述两种非等距GM(1, 1)模型以外,笔者也提出了一种非等距GM(1, 1)模型,可用于沉降的分析预测[8]。该模型与加权非等距GM(1, 1)模型最大的区别在于其拟合函数为指数函数。考虑到沉降数据本身具有累加性质,在建立非等距GM(1, 1)模型时,并未对沉降数据进行累加,而是将其视为非等距GM(1, 1)模型的一次累加数据。其建模原理如下[8]。
记原始变形监测序列为:
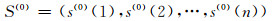
|
(2) |
对应的时间序列为:
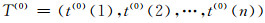
|
(3) |
上述序列的一次累减值为:
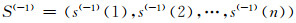
|
(4) |
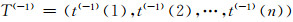
|
(5) |
按照灰色系统理论,白化方程为:
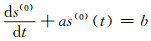
|
(6) |
其时间响应序列为:
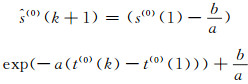
|
(7) |
按照灰色系统理论,可建立对应的灰微分方程:
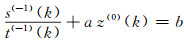
|
(8) |
式中,z(0)(k)为背景值,一般取z(0)(k)=0.5(s(0)(k)+s(0)(k-1))。
根据最小二乘法可估计参数a、b:

|
(9) |
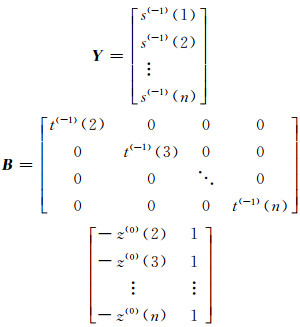
|
(10) |
从式(10)可以看出,非等时距GM(1, 1)模型相对于传统GM(1, 1)模型,在参数求解上仅多了时间序列参数矩阵。由于采用原始数据直接建模,所以利用式(7)即可进行预测。再看灰色线性回归组合模型的预测式[5]:
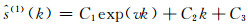
|
(11) |
对式(11)进行一次累减,可得原始数据的预测式:
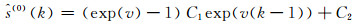
|
(12) |
对比式(7)和式(12)可以看出,两者都是指数函数,具有等效性,只是在参数的求解上存在不同。同时,式(7)不仅可以用于等时间间隔数据,也可以用于非等时间间隔数据。因此,该模型可代替灰色线性回归组合模型用于近似指数趋势的沉降数据的分析预测。
2.2 模型的改进背景值z(0)(k)一般可取紧邻均值形式,但会导致模型存在固有缺陷。笔者对此进行了改进,提出了加权背景值形式[8],文献[10]则给出了背景值及权重的具体表达式:
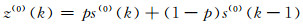
|
(13) |
式中,p=f(t(-1)(k), β)=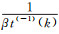
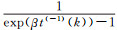
在该背景值下,非等距GM(1, 1)模型满足白指数率预测重合性,可用于近似非齐次指数序列的分析和预测。背景值的推导过程如下:
将式(7)连续化有s(0)(t)=Aexp(βt)+B,则:
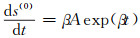
|
(14) |
对比式(6)和式(8),取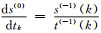
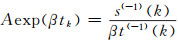
|
(15) |
由s(0)(k)=Aexp(β(t(0)(k)-t(0)(1)))+B和s(0)(k-1)=Aexp(β(t(0)(k-1)-t(0)(1)))+B,有:
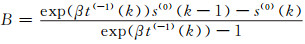
|
(16) |
将式(14)和式(16)代入s(0)(tk)=Aexp(βtk)+B,可得:

|
(17) |
整理式(17)可得式(13),在该背景值下,式(6)和式(8)具有一致性。
2.3 参数求解将背景值式(13)代替原参数求解式(8)中的背景值,即可确定非等距GM(1,1)模型的参数。但是新背景值式(13)与权重p有关,而权重p是t0(k)、β的函数,t0(k)已知,而β未知。由于t0(k)不是定值,所以背景值权重并非定权,而是β的函数。为此,需要求解参数β,以确定参数a、b。
显然,当原始数据序列为指数序列时,有β=-a。对于近似指数序列,可以首先取p=0.5,计算得到a1,再取β1=-a1,计算得到a2。比较a1与a2之间的差异,若差异很小,则认为此时计算的参数可以用于分析预测;若差异较大,继续按照β=-a计算,直到an和an-1非常接近。
3 实例分析GM(1, 1)模型的预测式是齐次指数函数,笔者所建立的非等距GM(1, 1)模型的预测式为非齐次指数函数,它们是否得到良好的拟合预测效果,完全取决于原始数据是否接近于齐次或非齐次指数序列,这是建模的前提。地基沉降数据一般为近似指数序列,常用Asaoka公式进行地基沉降的分析预测[10],其由基于一维固结问题的Mikasa固结方程推导而来[11],具有明确的物理意义。可以证明式(6)同Asaoka的一阶微分方程具有一致性[10],所以笔者所建立的非等距GM(1, 1)模型可代替Asaoka法用于地基沉降的分析预测。
在进行实例分析前,为了方便进行对比,做如下定义:笔者所建立的非等距GM(1, 1)模型为模型Ⅰ,加权非等距GM(1, 1)模型为模型Ⅱ,灰线性加权非等距GM(1, 1)模型为模型Ⅲ。
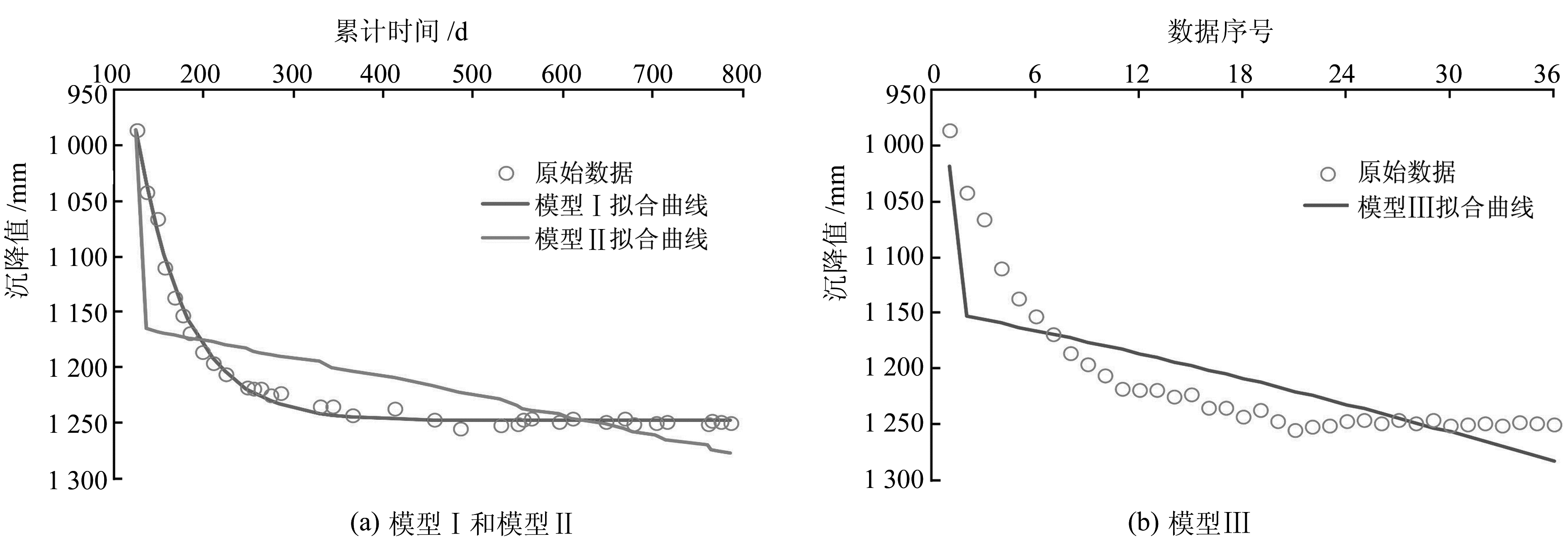
3.1 实例1以深圳机场软基处理试验堤B区S7沉降板的沉降观测记录为例[12],该沉降数据为非等距序列,具体数据见文献[12]。以该数据建立模型Ⅰ,并预测最终沉降量,即式(7)中的b/a。同时,为了进行对比分析,建立模型Ⅱ和模型Ⅲ。3种模型拟合结果如图 3所示。从图 3(a)可以看出,模型Ⅰ拟合效果良好,根据其拟合函数预测最终沉降为1 248.2 mm,Asaoka法预测最终沉降为1 253 mm,实测沉降稳定值为1 249 mm,三者相差不大,说明模型Ⅰ同Asaoka法一样可用于沉降的分析预测。而模型Ⅱ的拟合结果与实际结果相差较大,并且沉降发展不具备收敛趋势,不可预测最终沉降量。从图 3(b)可以看出,模型Ⅲ以模型Ⅱ的拟合序列作为原始序列,所以其拟合曲线与模型Ⅱ的拟合曲线在形态上类似,拟合效果同样不佳。同时,模型Ⅲ将沉降序列视为等间隔序列,模型预测式与时间无关,不可预测最终沉降量。
|
图 3 沉降观测原始数据与拟合曲线 Fig. 3 The observation subsidence and fitting curve |
以成绵乐铁路客运专线DK171 +600测点观测结果为例[13],该沉降数据为非等距序列,具体数据见文献[13]。以该数据建立模型Ⅰ、模型Ⅱ和模型Ⅲ,3种模型拟合结果如图 4所示。从图 4(a)中可以看出,模型Ⅰ拟合效果良好,拟合相关系数为0.995> 0.92,满足《客运专线铁路无砟轨道铺设条件评估技术指南》中关于曲线回归的相关系数不低于0. 92的要求。根据其拟合函数预测,最终沉降为3.66 mm,与最后一级沉降量对比有3.50/3.66 = 95.6% > 75%,满足《指南》中关于路基填筑完成或堆载预压完成后已产生的沉降占预测最终沉降的比例不小于75%的要求。而模型Ⅱ的拟合结果与实际结果相差较大,并且沉降发展不具备收敛趋势,不可预测最终沉降量。从图 4(b)可以看出,模型Ⅲ拟合效果同样不佳,模型预测式与时间无关,不可预测最终沉降量。

|
图 4 沉降观测原始数据与拟合曲线 Fig. 4 The observation subsidence and fitting curve |
1) 加权非等距GM(1, 1)模型的拟合结果并非指数序列,而GM(1, 1)模型的拟合结果为指数序列,两者之间具有矛盾性。对于具有近似指数趋势的沉降数据,不适用于加权非等距GM(1, 1)模型。
2) 文献[7]中所建立的灰线性加权非等距GM(1, 1)模型并非真正的非等距模型,模型预测式与时间无关,不能用于非等距沉降数据的分析预测。
3) 笔者所建立的非等距GM(1, 1)模型的预测式为指数函数,等效于灰色线性回归组合模型,可用于非等时距沉降数据的分析预测中。
| [1] |
文鸿雁, 周吕, 韩亚坤, 等. 基于卡尔曼滤波的GM(1, 1)模型在高铁隧道沉降变形分析中的应用[J]. 大地测量与地球动力学, 2014, 34(1): 88-91 (Wen Hongyan, Zhou Lü, Han Yakun, et al. Study on GM(1, 1) Modeling for Prediction of Deformation under Different Initial Conditions[J]. Journal of Geodesy and Geodynamics, 2014, 34(1): 88-91)
(  0) 0) |
| [2] |
陈威, 唐德燕, 张届. 利用三点法-灰色组合模型预测铁路路基沉降[J]. 测绘科学, 2015, 40(7): 37-40 (Chen Wei, Tang Deyan, Zhang Jie. Application of Three-Point-Method-Grey GM(1, 1) Combination Model in Settlement Prediction for a Railway Line[J]. Science of Surveying and Mapping, 2015, 40(7): 37-40)
(  0) 0) |
| [3] |
高彩云, 崔希民, 高宁. 顾及不同初始条件的GM(1, 1)变形建模研究[J]. 大地测量与地球动力学, 2014, 34(4): 157-160 (Gao Caiyun, Cui Ximin, Gao Ning. Study on GM(1, 1) Modeling for Prediction of Deformation under Different Initial Conditions[J]. Journal of Geodesy and Geodynamics, 2014, 34(4): 157-160)
(  0) 0) |
| [4] |
李克昭, 李志伟, 孟福军. 基于综合优化GM(1, 1)的形变预测模型[J]. 大地测量与地球动力学, 2016, 36(2): 120-123 (Li Kezhao, Li Zhiwei, Meng Fujun, et al. Deformation Forecasting Model Based on Synthetic and Optimized GM(1, 1)[J]. Journal of Geodesy and Geodynamics, 2016, 36(2): 120-123)
(  0) 0) |
| [5] |
王钟羡, 吴春笃, 史雪荣. 非等间距序列的灰色模型[J]. 数学的实践与认识, 2003, 33(10): 16-20 (Wang Zhongxian, Wu Chundu, Shi Xuerong. A Gray Model for Non-equidistant Sequence[J]. Mathematics in Practice and Theory, 2003, 33(10): 16-20 DOI:10.3969/j.issn.1000-0984.2003.10.004)
(  0) 0) |
| [6] |
李翠凤, 戴文战. 非等间距GM(1, 1)模型背景值构造方法及应用[J]. 清华大学学报:自然科学版, 2007, 47(增2): 1 729-1 732 (Li Cuifeng, Dai Wenzhan. Determinator of the Background Level in the Non-Equidistant GM(1, 1) Model[J]. Journal of Tsinghua University(Science & Technlogy), 2007, 47(S2): 1 729-1 732)
(  0) 0) |
| [7] |
李克昭, 李志伟, 丁安民, 等. 灰线性加权非等距GM(1, 1)形变预测模型[J]. 大地测量与地球动力学, 2016, 36(6): 513-516 (Li Kezhao, Li Zhiwei, Ding Anmin, et al. Deformation Prediction Model of Gray Line Weighted Non-Equidistance GM(1, 1)[J]. Journal of Geodesy and Geodynamics, 2016, 36(6): 513-516)
(  0) 0) |
| [8] |
陈鹏宇, 段新胜. 建筑物沉降的非等间隔GM(1, 1)模型的建立与改进[J]. 工程勘察, 2010(3): 77-80 (Chen Pengyu, Duan Xinsheng. Establishment and Improvement of Non-Equal Interval GM(1, 1) Model of Building Subsidence[J]. Geotechnical Investigation & Surveying, 2010(3): 77-80)
(  0) 0) |
| [9] |
张俊中, 雷伟伟, 王睿, 等. 灰线性回归模型在建筑物沉降分析中的应用[J]. 河南科学, 2015, 33(3): 416-420 (Zhang Junzhong, Lei Weiwei, Wang Rui, et al. Application of GM(1, 1) and Line Regression Model in the Deformation of Building[J]. Henan Science, 2015, 33(3): 416-420)
(  0) 0) |
| [10] |
潘翔. 地基沉降预测的两种灰色模型与Asaoka法[J]. 地下空间与工程学报, 2013, 9(6): 1 443-1 448 (Pan Xiang. Asaoka Method and Two Grey Models in the Forecast of Groundsill Settlement[J]. Chinese Journal of Underground Space and Engineering, 2013, 9(6): 1 443-1 448)
(  0) 0) |
| [11] |
Asaoka A. Observational Procedure of Settlement Prediction[J]. Soils and Foundations, 1978, 18(4): 87-101 DOI:10.3208/sandf1972.18.4_87
(  0) 0) |
| [12] |
李福民, 赵有明. 深圳软土地基处理中Asaoka法的应用[J]. 中国铁道科学, 2002, 23(4): 38-42 (Li Fumin, Zhao Youming. Application of Asaoka Method in Soft Ground Improvement in Shenzhen[J]. China Railway Science, 2002, 23(4): 38-42 DOI:10.3321/j.issn:1001-4632.2002.04.008)
(  0) 0) |
| [13] |
牛欣欣. 路基沉降预测的非等间隔Asaoka法[J]. 公路工程, 2013, 38(6): 241-244 (Niu Xinxin. Non-equal Interval Asaoka Method for Predicting Subgrade Settlement[J]. Highway Engineering, 2013, 38(6): 241-244)
(  0) 0) |
 2017, Vol. 37
2017, Vol. 37

