2. 广西精密导航技术与应用重点实验室,桂林市金鸡路1号,541004
精确、可靠的室内导航定位是一个具有挑战性的问题。近年来基于地磁场的室内定位技术作为“无源”定位的新方向,逐渐引起人们的关注。其中高精度的地磁基准图是室内地磁辅助定位成功的关键。前人的研究多着眼于网格插值法,文献[1-2]对局部区域制备地磁图的几种网格插值算法进行评估,实验结果显示,克里金法具有较高的插值精度。本文选取3种克里金插值算法与标准高斯过程回归算法进行实验对比,结果表明,协同克里金法有更高的精度,标准高斯过程回归算法有更好的实时性。
1 地磁建模的4种算法由于室内地磁场具有时域稳定性、空间变化多样性等特点[3-4],一般利用空间统计学方法得到相应空间的磁场要素。空间统计学通过研究对象在空间上不同位置的抽样点上的差异,定量描述其空间变化规律。其预测法主要有多元回归法、普通克里金插值、协同克里金插值、双线性内插等。本文选取4种常见的算法进行比较,选取3个性能指标进行分析,并在结论中给出最合适的选取方案。
1.1 普通克里金插值普通克里金插值法[5](ordinary Kriging, OK)是一种用于空间插值的统计算法,其主要思想就是用高斯随机场[6](Gaussian random field, GRF)来实现响应曲面。因为在空间连续性变化的属性是非常不规则的,不能简单地用平滑的数学函数进行模拟,而应采用随机曲面进行描述。普通克里金插值基于如下假设:
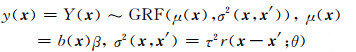
|
(1) |
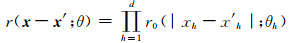
|
(2) |
式中,x为空间坐标矢量,b通常是关于x的多项式,β、τ2和θ为未知参数。
式(2)是空间相关函数,对应于常说的变差函数,其中r0通常是一个减函数,且θh控制着h维距离测量的相关度量。选定b和r0(t; θ)来构建相关函数,使用最大似然估计来选择β、τ2和θ。假设参数β、τ2和θ已知,那么克里金插值的预测结果为:
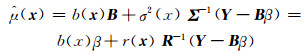
|
(3) |
其中σ2(x)是行向量,它的元素是σ2(x, xi),外部方差函数为Σ,Σhi=σ2(xh, xi),B =b(xi),Y =[Y(x1), …, Y(xk)]T,r (x) =σ2(x)/τ2,R= Σ/τ2。
1.2 标准高斯过程回归对于高斯过程[7](standard Gaussian process regression, SGPR), 可以理解为将多元高斯分布扩展到无限维,其性质可由期望和协方差函数表示。对于y(x)~GP(m(x), k(x, x′)),通常可表示如式(4),这里选择平方指数函数(类似SVM里的高斯核)作为协方差函数:

|
(4) |
式中,x和x′为任意的随机变量,l、σy2和σn2(三者为通常所说的超参数)需要训练得到。考虑到实际观测数据中存在噪声,如y(x)=Y(x)+ε, ε~N(0, σn2),则其协方差函数为:
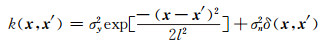
|
(5) |
式中,δ(x, x′)为罗内克δ函数。
1.3 随机克里金插值随机克里金插值法[8](stochastic Kriging, SK)基于以下假设:

|
(6) |
式中,Y和ε是独立的,其思想是将模型误差考虑在内。鉴于高斯随机场的均方函数和误差函数,预测结果是:
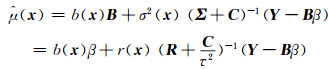
|
(7) |
式中,C为内部协方差矩阵,由Chi=c(xh, xi)给出,矢量r(x)(R + C/τ2)-1可以理解为插入的权值。如果σ2已知、β未知,则用最大似然估计算法(maximum likelihood estimation, MLE)进行估计:
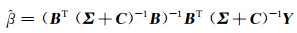
|
(8) |
协同克里金插值法[9](co-Kriging, CK)针对模型数据有效性衡量预测精度,下文实验部分采用自回归协同克里金模型[10]。协同克里金模型分别构建两个普通克里金插值模型。首先将样本数据分为两部分,其中可信度高的记为(Xb, yb),次之的记为(Xu, yu)。然后分别对(Xu, yu)和(Xb, yb-ρμu(Xb))用普通克里金插值算法进行建模,分别记为Yu(x)和sY(x)。其中ρ作为第二个克里金模型的估计参数。
其插值结果与式(1)相似:
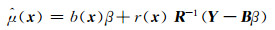
|
(9) |
式中,r (x)和R都是μu(x)和μs(x)的函数,形式如下:
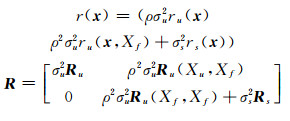
|
本文设计两种场景进行实验,两种场景分别为长度与宽度相差较大的走廊形和长度与宽度相差不大的菱形。采集三轴地磁数据,并选取均方差、交叉验证法和积分均方误差等3项参数对4种算法进行比较与分析。
2.1 采集实验数据本文数据采集所选用的地磁传感器型号为AMK8963,解析度为1.5 mGauss,实验网格大小设置为0.5 m×0.5 m,采样率为20 Hz。图 1为情景1数据采集路线。地磁场包含7个特征量,即地磁场总强度F、水平强度H、垂直强度Z、H的北向分量X和东向分量Y、磁偏角D和磁倾角I。由于利用其中3个便可确定其余特征,故本实验中只采集X、Y、Z3个磁场特征量。

|
图 1 场景1数据采集路线 Fig. 1 Data acquisition route of scene 1 |
本文所采用的判别标准如下:
1) 均方差(root mean squared error, RMSE):
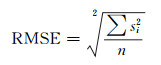
|
(10) |
该统计参数也叫回归系统的拟合标准差。我们所有的误差参数都是基于预测值和原始值之间的误差(即点对点),所有的误差都是相对原始数据平均值而展开的(即点对全)。
2) 交叉验证法(leave-one-out cross validation, LooCV):

|
(11) |
式中,H:, i、Hi, :代表ith列和ith行,Hi, i代表ith对角线元素。
3) 积分均方误差(integrated mean squared error, IMSE)[12]:
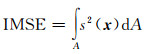
|
(12) |
式中,A代表输入。由于这个积分无法给出解析解,一般采用梯形法数值积分和蒙特卡洛采样[12](本文采用)求解。
2.3 实验数据分析表 1采用3个性能指标进行分析。对于同一种场景,首先从均方误差数据来看,协同克里金法均方根误差较小,有较好的插值效果;在交叉验证指标中,普通克里金法误差最小,表明普通克里金法有更好的“模型泛化”能力;在积分均方误差指标中,普通克里金法精度最高,说明其对于样本具有较强的整体度量,有更强的全局优化效果。综合来看,协同克里金法更适用于室内地磁图的构建。
|
|
表 1 数据分析 Tab. 1 Data analysis |
由表 1可见,对于两种不同的场景,在菱形场景中标准高斯过程回归和普通克里金插值两种算法在交叉验证法和积分均方误差指标中有较好表现,说明其对于长、宽约束力区别大的场景不适用;但协同克里金法综合表现依然是最好的,两种场景下均有较好的性能。另外,表 1中出现随机克里金指标异常,其原因为:1)在实际应用中,平方指数函数作为协方差函数效果不如Matérn类函数[13];2)样本点数较少、采样稀疏,且随机克里金模型参数较多,参数训练中误差较大。
表 2列出了各个算法协方差函数的选取及模型解算耗时与地磁图建立耗时的数据。从耗时上来看,标准高斯过程回归的耗时最少,协同克里金法耗时最多。由于克里金法采用最大似然估计进行求参,而标准高斯过程回归采用最大后验估计求参,融入了参数的先验分布,所以有更快的收敛速度。菱形场景中,标准高斯过程回归与协同克里金法精度接近,但标准高斯过程回归的解算速度比协同克里金法快3倍,更适用于构建地磁基准图;走廊形场景中,协同克里金法综合性能最好。图 2为协同克里金插值效果,图 3为磁场强度在水平面的投影。
|
|
表 2 算法分析 Tab. 2 Algorithm analysis |

|
图 2 协同克里金插值效果图 Fig. 2 Co-Kriging interpolation effect |

|
图 3 协同克里金法与标准高斯过程回归法的对比 Fig. 3 Co-Kriging method compared with SGPR method |
走廊形场景中,协同克里金法均方根误差较小,具有较好的插值效果,且对于样本具有较强的整体把握,有更强的优化效果,更适用于室内地磁基准图的构建,缺点是耗时较多;菱形场景中,虽然标准高斯过程回归与协同克里金法精度接近,但标准高斯过程回归耗时最少,对于实时性要求高的情况,标准高斯过程回归更满足需求。
| [1] |
张晓明, 赵剡. 基于克里金法插值的局部地磁图的构建[J]. 电子测量技术, 2009, 32(4): 122-125 (Zhang Xiaoming, Zhao Yan. Local Geomagnetic Field Mapping Based on Kriging Interpolation Method[J]. Electronic Measurement Technology, 2009, 32(4): 122-125 DOI:10.3969/j.issn.1002-7300.2009.04.033)
(  0) 0) |
| [2] |
杨功流, 张桂敏, 李士心. 泛克里金插值法在地磁图中的应用[J]. 中国惯性技术学报, 2008, 16(2): 162-166 (Yang Gongliu, Zhang Guimin, Li Shixin. Application of Universal Kriging Interpolation in Geomagnetic Map[J]. Journal of Chinese Inertial Technology, 2008, 16(2): 162-166)
(  0) 0) |
| [3] |
Grand E L, Thrun S. 3-Axis Magnetic Field Mapping and Fusion for Indoor Localization[C].Multisensor Fusion and Integration for Intelligent Systems, 2012 https://www.researchgate.net/publication/261424001_3-Axis_magnetic_field_mapping_and_fusion_for_indoor_localization
(  0) 0) |
| [4] |
Frassl M, Angermann M, Lichtenstern M, et al. Magnetic Maps of Indoor Environments for Precise Localization of Legged and Non-Legged Locomotion[J]. IEEE/RSJ International Conference on Intelligent Robots and Systems, 2013, 40(6): 913-920
(  0) 0) |
| [5] |
Giraldo R, Delicado P, Mateu J. Ordinary Kriging for Function-Valued Spatial Data[J]. Environmental & Ecological Statistics, 2011, 18(3): 411-426
(  0) 0) |
| [6] |
Siegmund D O, Worsley K J. Testing for a Signal with Unknown Location and Scale in a Stationary Gaussian Random Field[J]. Annals of Statistics, 2010, 48(7): 695-700
(  0) 0) |
| [7] |
Banerjee S, Gelfand A E, Finley A O, et al. Gaussian Predictive Process Models for Large Spatial Data Sets[J]. Journal of the Royal Statistical Society, 2008, 70(4): 825-848 DOI:10.1111/rssb.2008.70.issue-4
(  0) 0) |
| [8] |
Wang B, Bai J, Gea H C, et al.Stochastic Kriging for Random Simulation Metamodeling with Finite Sampling[C]. ASME 2013 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, 2013
(  0) 0) |
| [9] |
Nerini D, Monestiez P, Manté C. Cokriging for Spatial Functional Data[J]. Journal of Multivariate Analysis, 2010, 101(2): 409-418 DOI:10.1016/j.jmva.2009.03.005
(  0) 0) |
| [10] |
Kennedy M C, O'Hagan A. Predicting the Output from a Complex Computer Code when Fast Approximations Are Available[J]. Biometrika, 2000, 87(1): 1-13 DOI:10.1093/biomet/87.1.1
(  0) 0) |
| [11] |
Nadaraja E A. On the Integral Mean Square Error of Some Nonparametric Estimates for the Density Function[J]. Theory of Probability & Its Applications, 1974, 19(19): 133-141
(  0) 0) |
| [12] |
Martínez-Rovira I, Sempau J, Prezado Y. Monte Carlo-Based Dose Calculation Engine for Minibeam Radiation Therapy[J]. Physica Medica, 2014, 30(1): 57-62
(  0) 0) |
| [13] |
Stein M L. Interpolation of Spatial Data: Some Theory for Kriging[M]. New York: Springer, 1999
(  0) 0) |
2. Guangxi Key Laboratory of Precision Navigation Technology and Application, 1 Jinji Road, Guilin 541004, China
 2017, Vol. 37
2017, Vol. 37



