2. 武汉大学测绘学院,武汉市珞喻路129号,430079
EGM2008是由美国国家地理空间情报局研制的全球超高阶地球重力场模型,可方便地根据点位的经纬度计算出高程异常[1-4]。该模型的高程异常全球精度为13 cm,在我国大陆总体精度为20 cm[1],但尚未见针对EGM2008在新疆地区的精度评价,因此测试研究EGM2008模型高程异常在新疆地区的精度及误差分布特点,对于在新疆地区把高精度的GPS大地高转换为工程建设所需要的正常高具有重要意义。
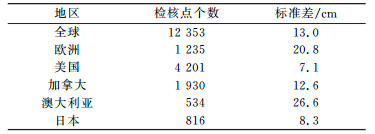
1 EGM2008模型的精度情况及国内应用情况 1.1 EGM2008模型高程异常在全球的精度情况EGM2008模型研制周期长达4 a,期间曾委托多个国家和地区对过渡模型进行测试与评估。表 1为EGM2008在全球及各地区的精度情况[5]。
|
|
表 1 EGM2008模型在全球的精度情况 Tab. 1 The precision of EGM2008 around world |
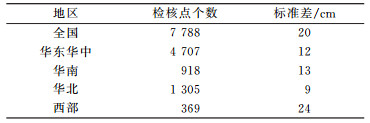
国内有很多学者及工程技术人员开展了EGM2008求解高程异常的精度分析,但由于测试地区、数据样本、采用的方法不同(相对精度、绝对精度),所检验得到的EGM2008模型的精度也不尽相同。在消除系统偏差后,精度在2.8~48 cm之间[6-9],其中中国测绘科学研究院章传银等[1]的研究采用的数据量最大,分布最广,最具代表性,其研究结果见表 2。
|
|
表 2 EGM2008模型在全国的精度情况 Tab. 2 The precision of EGM2008 throughout China |
国内关于EGM2008模型导出高程异常的应用研究主要集中在利用EGM2008模型进行区域似大地水准面精化,及在工程中基于EGM2008模型进行GPS高程转换以替代水准测量两个方面。从行业上看,城市测绘、石油物探测量、铁路测量领域的应用研究居多,除城市测绘由于数据量大且覆盖全测区,后续测绘区域相对固定的特点可以直接在现有研究基础上应用外,工程中的研究和测试成果由于数据量小,受地域限制,仅具有参考意义。这是因为EGM2008模型的精度是随着空间变化而变化的,在应用时还需验证测试[10-12]。
2 EGM2008求解高程异常在新疆的精度分析 2.1 精度分析评价方法采用NGA的官方网站提供的EGM2008模型计算程序hsynth_WGS84.exe计算WGS-84经纬度对应点的高程异常值ζ,再求出各点的正常高H正常。通过计算得到的正常高经常会存在系统偏差ΔH,ΔH主要因单点定位获取的大地高H与真实值的差异引起,同时还包含了某一国家或区域定义的高程基准与EGM2008模型定义的全球高程基准并不能完全精准匹配存在的差异[13],则高程转换公式为:
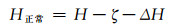
|
(1) |
根据高程异常曲面同样均衡性的特点,参照文献[14]提出的方法,即假设同一GPS控制网中有一基准点正常高h基已知,并且h基=H基-ζ基-ΔH,可得:
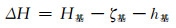
|
(2) |
在实际计算时,根据控制点的分布情况选取位于测区中部的GPS水准点作为基准点。基准点的引入消除了局部高程基准和全球大地水准面间的系统偏差的影响,能反映利用GPS大地高和EGM2008模型进行高程转换的精度。假设已知的水准点的高程为真值,将计算出的各GPS点正常高与实测的水准高程比较,得出差值即高程异常误差Δ,即可计算EGM2008模型高程异常精度的标准差:
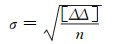
|
(3) |
分别统计每一测区和全部测区的最大值、最小值、平均值以及标准差,以反映EGM2008在每个区域的相对精度情况。
2.2 资料收集为评价新疆地区EGM2008模型的精度,笔者历时两年,共收集了分布于新疆13个地州38个测区的998个GPS水准点(GPS水准点在这里为合成词,意为联测了水准高程的GPS点)数据,数据的分布情况详见图 1。这些数据施测时间为2004~2015年,面状测区多为水利工程施工控制网数据,带状测区多为引水工程设计阶段的四等(D级)GPS网,执行规范为《水利水电工程测量规范》、《全球定位系统(GPS)测量规范》,高程等级除测区2和测区27外均为四等以上水准测量成果,大地高相对精度(相对于控制网中假定的某个已知点的大地高精度)最低为9.3 cm。
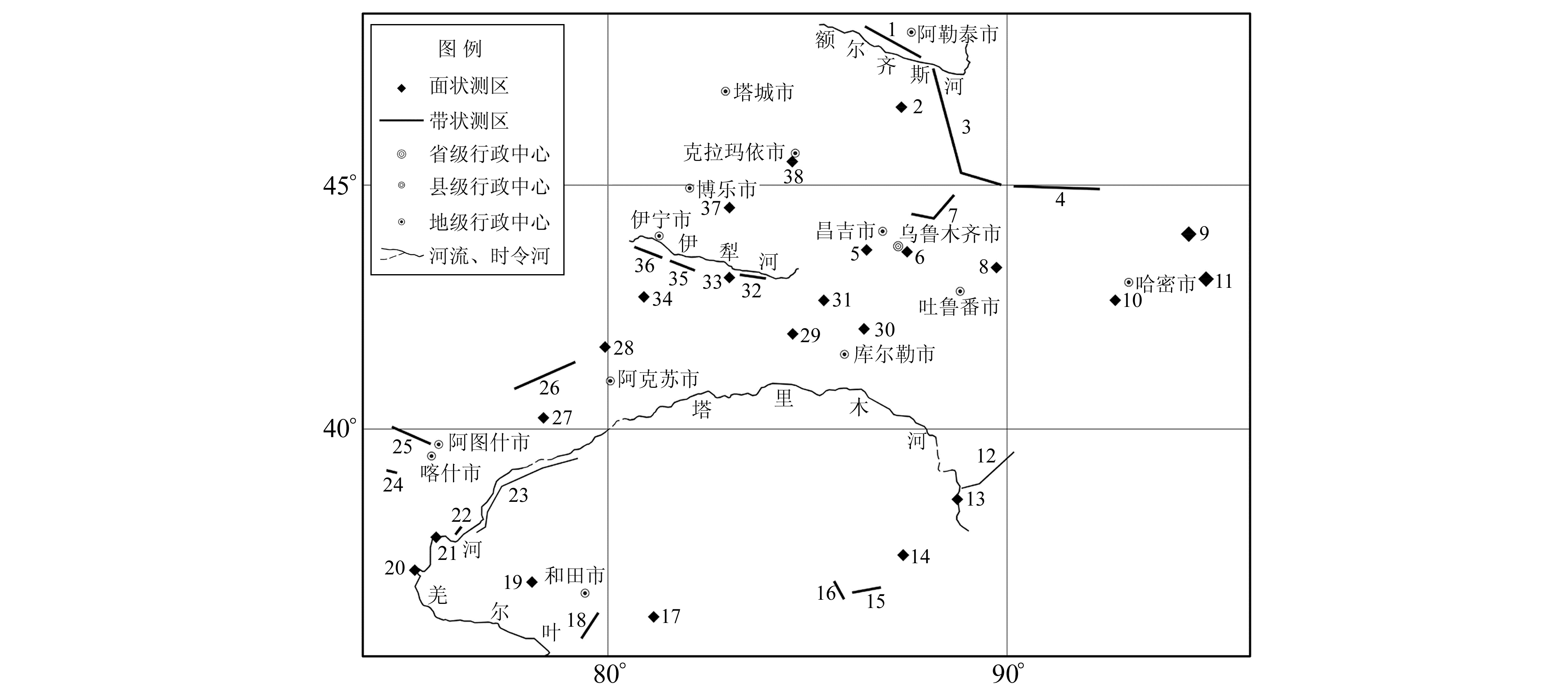
|
图 1 GPS水准数据测区分布 Fig. 1 The field distribution of GPS leveling data |
因所收集到的数据均无WGS-84已知数据,所有大地高均为控制网内某点单点定位所得大地高为已知参考值的相对独立数据,故本文讨论的结果为EGM2008模型的相对精度。所收集到的数据分布于全疆南北,地形多样,高程变化为500 ~4 000 m,基本能代表新疆的地形特点。
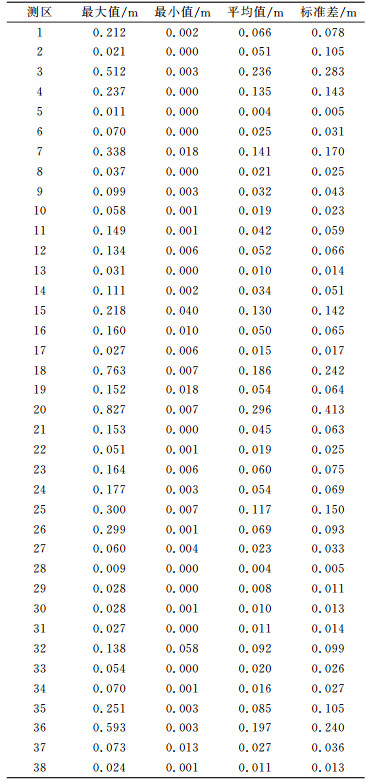
2.3 结果统计分析将38个测区的960个点(总点数998减去38个基准点)的高程异常误差值进行统计计算,各测区的误差特征值见表 3,全部测区的标准差为0.146 m,比文献[1]中得出的西部0.24 m和全国0.20 m的精度略高。统计精度高于文献[1]的原因与本文所采用的数据分布及引入基准点改正的方法有关。
|
|
表 3 GPS水准检核结果统计 Tab. 3 The statistics of GPS leveling data |
|
|
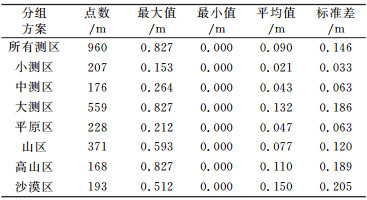
表 4 分组统计结果 Tab. 4 The statistics of GPS leveling dada in groups |
为了排除小区域数据对统计结果的影响以及分析EGM2008模型精度与地形类别的关系,采取分组的方法分别进行统计,分组统计结果见表 4。分组方案为:1)按测区大小分组,测区半径小于5 km的划分为小测区,半径介于5~10 km的为中测区,半径大于10 km的为大测区;2)按测区所在的地形类别分组,分为平原区、山区、高山区、沙漠区4类。
为分析EGM2008模型计算出的高程异常相对误差与空间分布的关系,绘制38个测区的误差分布与坐标关系图;为分析EGM2008模型高程异常相对误差与基准点距离的关系,绘制高程异常误差与距离关系图(绘图时根据测区走向以基准点为界区分距离正负)。所有测区均绘制了上述图表,由于篇幅所限,文中只列出有代表性的一个带状测区和一个面状测区(见图 2和图 3。图 3中以气泡大小表示误差的大小(相对值),空心为负值,实心为正值)。可以看出,EGM2008高程异常误差与空间分布有着较强的相关性,在一定范围内变化缓慢且连续,有着较明显的趋势,在较大的测区误差虽说随着距离的增加而变大,但是都出现了波形变化,并不会因为距离的变化而无限变大,变化范围为-0.85~0.80 m。
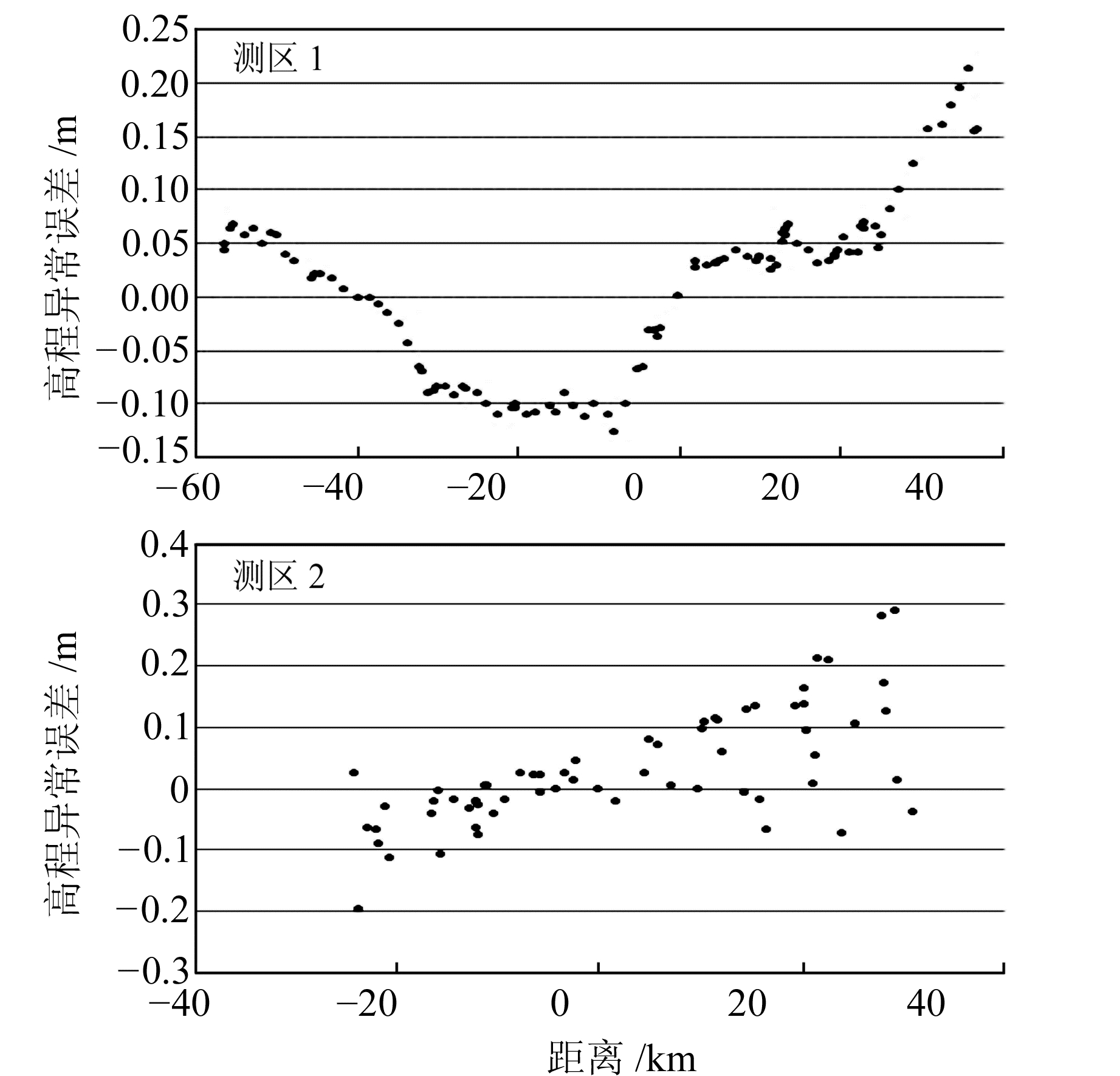
|
图 2 高程异常误差与基准点距离的关系 Fig. 2 Height anomaly error varies with the distance to base points |
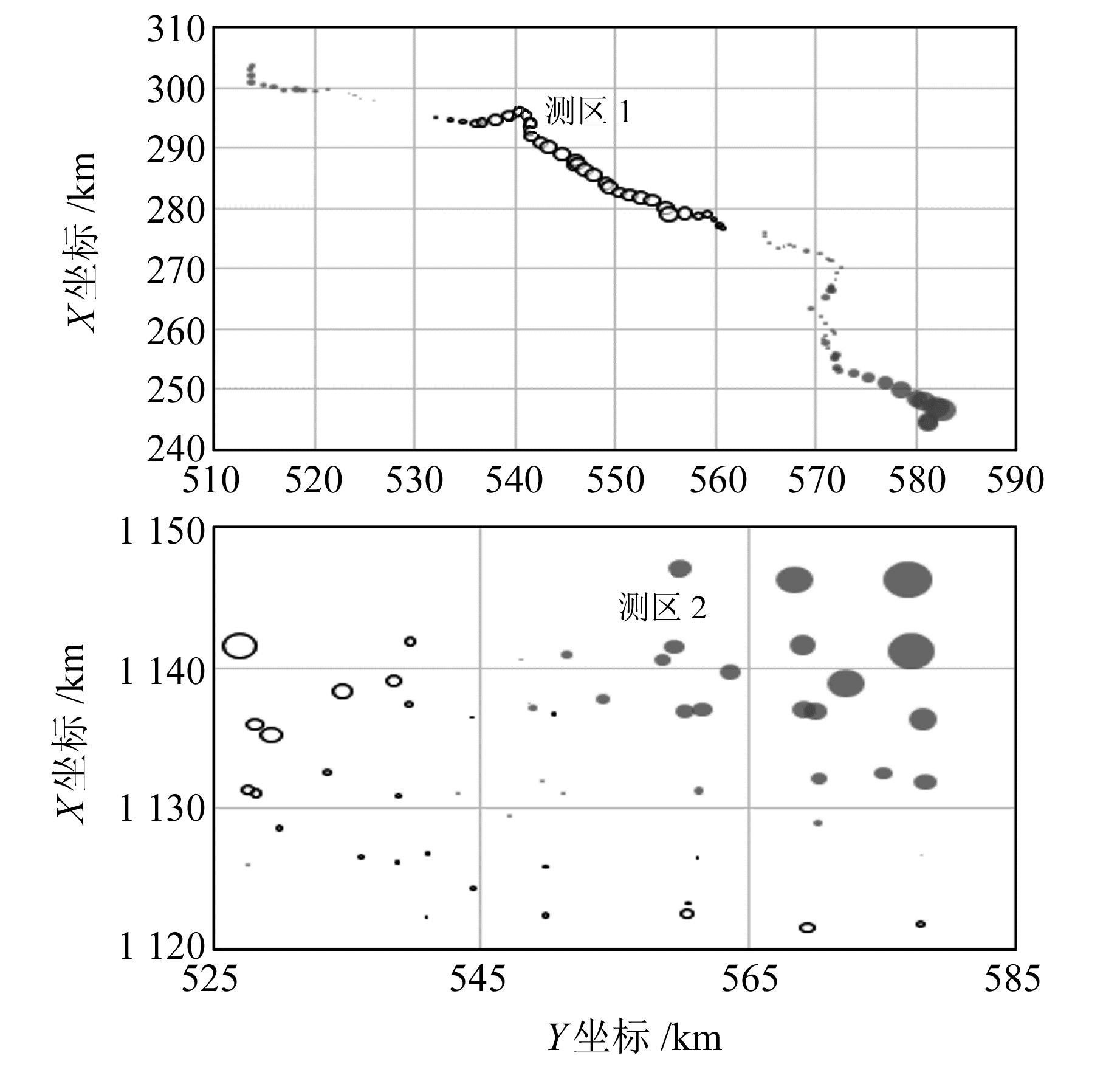
|
图 3 高程异常误差的平面分布 Fig. 3 Layout plan of height anomaly error |
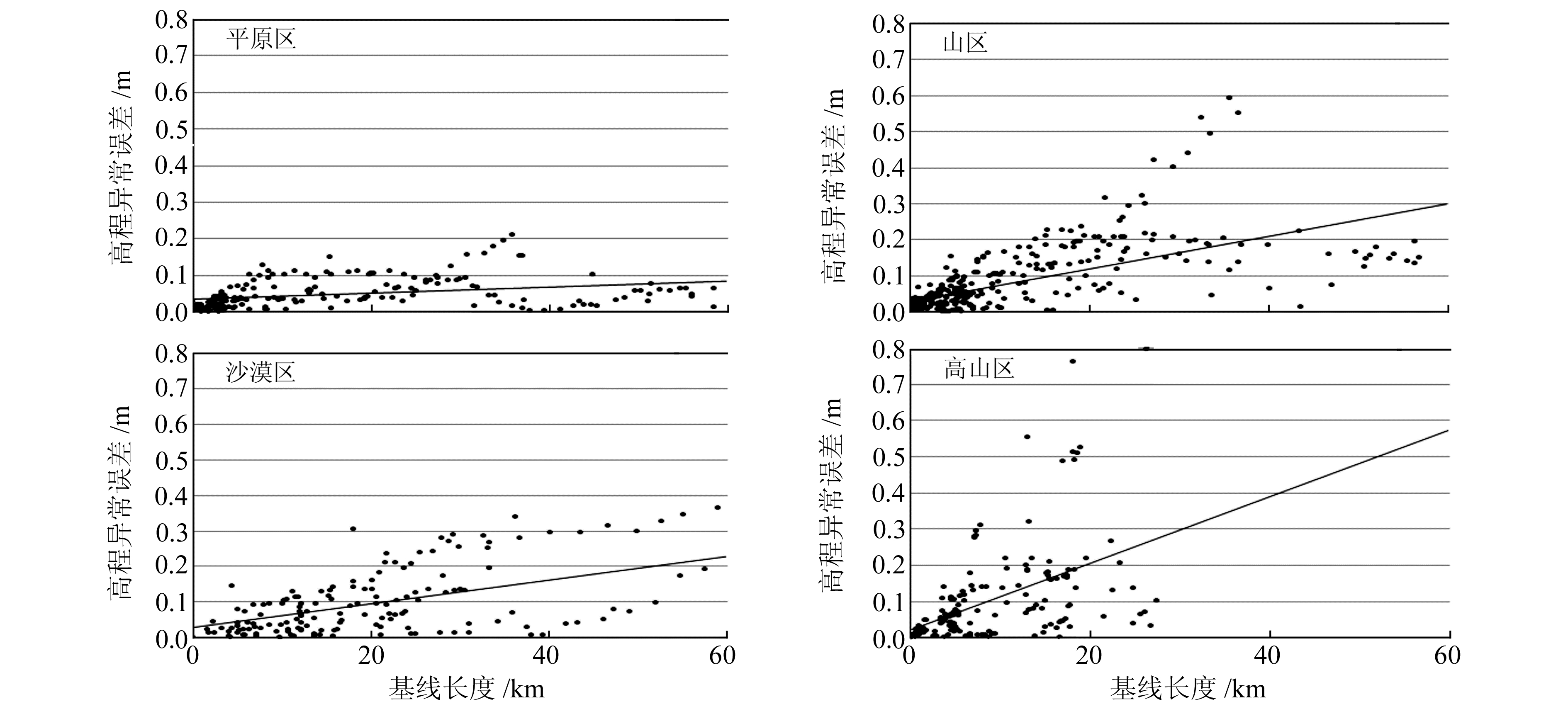
从图 4可以看出,EGM2008模型的精度随着基线(指GPS点与用于计算ΔH的基准点的距离)长度增加而增加,但是根据误差离散点用二次项拟合出的趋势线斜率不大,说明随着基线长度的增加精度下降并不快,而且在达到一定距离时下降速度有所减缓(图中约为40 km)。从图 5可以看出,EGM2008模型精度随着基线长度的增加,下降速度在高山区最快,沙漠区和山区次之,平原区下降最慢。
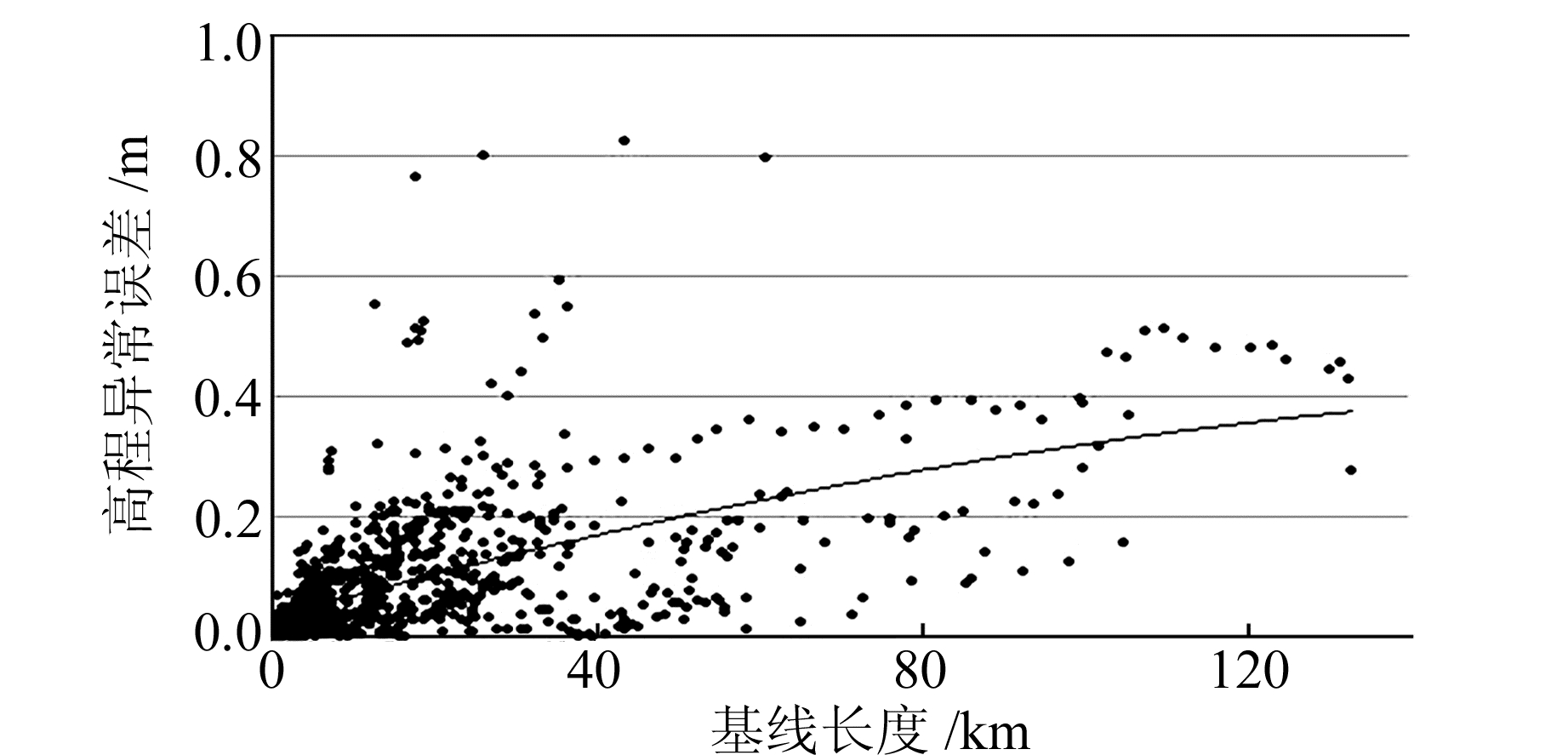
|
图 4 高程异常误差与基线长度的关系 Fig. 4 The relation between the height anomaly |
|
图 5 高程异常误差与基线长度的关系 Fig. 5 The relation between the height anomaly error and baseline length |
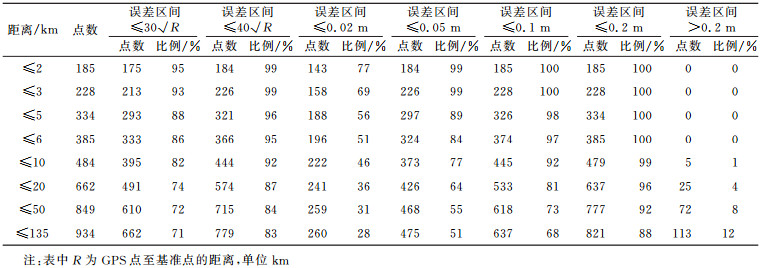
经统计,在半径小于5 km的范围内,点数为334,其中小于四等水准差的有293个,占88%(表 5);小于2倍检测限差的有329个,占98.5%;全部都在3倍限差以内。半径小于10 km的范围内,点数为484,其中小于五等水准检测限差的有444个,占92%(表 5);小于2倍检测限差的有479个,占99%;全部都在3倍检测限差以内。说明利用EGM2008进行GPS高程转换,引入一点基准点转换在5 km范围内可以代替四等水准,在10 km范围内可以代替五等水准。
|
|
表 5 不同基线长度EGM2008模型误差分布 Tab. 5 Error distribution of EGM2008 within different baseline length |
本文通过分布在全疆13个地州的38个测区998组GPS水准数据计算统计分析,得出如下结论:
1) EGM2008模型高程异常消除系统偏差后,在新疆地区的总体精度为0.146 m,其中平原区为0.063 m,山区为0.117 m,沙漠区为0.205 m,高山区为0.217 m。
2) EGM2008高程异常误差与空间分布有着较强的相关性,在一定范围内的变化缓慢且连续,趋势性较为明显。
3) EGM2008高程异常的相对精度随着距离的增加而降低,精度降低的速度与地形变化有关,平原地区精度下降慢,沙漠和山区次之,地形变化剧烈的高山区精度下降快。
4) 虽说EGM2008的高程异常相对精度随着距离的增加而降低,但并非呈线性单调增减,而是呈一定波形变化,在新疆地区这个界限在-0.85~0.80 m之间。
5) EGM2008的高程异常在较小的范围内(本文为半径5 km)相对精度为0.033 m(表 4),通过EGM2008模型计算得到的正常高,仅用一个点改正即可达到四等水准测量的精度;在半径为10 km的区域内,相对精度为0.063 m(表 4),用一个点改正可达到五等水准的精度。
6) 由于EGM2008模型可以免费获取,且计算简单,可广泛用于代替小区域的四等水准测量、五等水准测量、大范围中小比例尺地形图测绘的高程控制及精度要求较低的高程传递,以及水准测量的粗差探测等。
7) 应用EGM2008模型转换正常高时,为了避免基准点误差引起的系统偏差,建议尽量选取精度可靠(大地高及正常高)的点作为基准点,同时一个测区应有适当的检核点用于验证外部精度。
8) 代替水准测量时,测区半径在平原区可适当放宽,沙漠区和山区适当减小,高山区尤其是海拔高、相对高差大、地形变化剧烈的地区应谨慎使用,严格控制距离并加强检核。本文给出的建议是:平原区代替四等水准可放宽至20 km,代替五等水准可放宽至40 km;沙漠区和地形变化不是很大、海拔在2 000 m以下的山区代替四等和五等水准分别按5 km和10 km控制;海拔高于2 000 m、相对高差大、地形变化剧烈的高山区代替四等和五等水准分别按2 km和5 km控制。
9) 应用于高程精度要求高的大范围测区(如长距离路线工程)时,建议分块(段)改正,若能基于EGM2008模型采用“移去-拟合-恢复”法将会获得更好的精度,由于不属本文探讨的内容,未对该方法在新疆的应用效果进行测试,但是根据图 2的直观反映,应用该方法可行。
| [1] |
章传银, 郭春喜, 陈俊勇, 等. EGM2008地球重力场模型在中国大陆适用性分析[J]. 测绘学报, 2009, 38(4): 283-289 (Zhang Chuanyin, Guo Chunxi, Chen Junyong, et al. EGM2008 and Its Application Analysis in Chinese Mainland[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(4): 283-289 DOI:10.3321/j.issn:1001-1595.2009.04.001)
(  0) 0) |
| [2] |
Pavlis N K, Holmes S A, Kenyon S C, et al. The Development and Evaluation of the Earth Gravitational Model 2008(EGM2008)[J]. Journal of Geophysical Research: Solid Earth, 2012, 117(B4)
(  0) 0) |
| [3] |
Erol B, Erol S. Learning-Based Computing Techniques in Geoid Modeling for Precise Height Transformation[J]. Computers & Geosciences, 2013, 52: 95-107
(  0) 0) |
| [4] |
Pavlis N K, Holmes S A, Kenyon S C, et al. An Earth Gravitational Model to Degree2160: EGM2008[EB/OL].http://www.massentransporte.de/fileadmin/2kolloquium_muc/2008-10-08/Bosch/ EGM2008.pdf, 2008
(  0) 0) |
| [5] |
朱君俊.基于重力场模型EGM2008的高程拟合方法研究[D].呼和浩特: 内蒙古农业大学, 2012 (Zhu Junjun. Study on Elevation Fitting Method Based on EGM2008 Model[D]. Huhhot: Inner Mongolia Agricultural University, 2012)
(  0) 0) |
| [6] |
荣敏, 周巍, 陈春旺. 重力场模型EGM2008和EGM96在中国地区的比较与评价[J]. 大地测量与地球动力学, 2009, 29(6): 123-126 (Rong Min, Zhou Wei, Chen Chunwang. Evaluation of Gravity Field Models EGM2008 and EGM96 Applied in Chinese Area[J]. Journal of Geodesy and Geodynamics, 2009, 29(6): 123-126)
(  0) 0) |
| [7] |
束蝉方, 李斐, 郝卫峰. EGM2008模型在中国某地区的检核及适用性分析[J]. 武汉大学学报:信息科学版, 2011, 36(8): 919-922 (Shu Chanfang, Li Fei, Hao Weifeng. Evaluation of EGM2008 and Its Application Analysis over a Particular Region of China[J]. Geomatics and Information Science of Wuhan University, 2011, 36(8): 919-922)
(  0) 0) |
| [8] |
张兴福, 刘成, 刘红新. 利用GPS/水准数据检核EGM2008重力场模型的精度[J]. 测绘通报, 2009(2): 7-9 (Zhang Xingfu, Liu Cheng, Liu Hongxin. Accuracy Validation of EGM2008 Model Using GPS/Leveling Data[J]. Bulletin of Surveying and Mapping, 2009(2): 7-9)
(  0) 0) |
| [9] |
冯林刚, 赵军, 赵锁志. EGM2008模型在GPS高程转换中的应用研究[J]. 测绘信息与工程, 2009, 34(5): 6-7 (Feng Lingang, Zhao Jun, Zhao Suozhi. Application of EGM2008 Model in Conversion of GPS Elevation[J]. Journal of Geomatics, 2009, 34(5): 6-7)
(  0) 0) |
| [10] |
张兴福, 刘成. 综合EGM2008模型和SRTM/DTM2006[J]. 测绘学报, 2012, 41: 25-32 (Zhang Xingfu, Liu Cheng. The Approach of GPS Height Transformation Based on EGM2008 and SRTM/DTM2006.0 Residual Terrain Model[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(1): 25-32)
(  0) 0) |
| [11] |
管真, 陈剑杰, 尉伯虎, 等. 基于EGM2008的GPS水准拟合在复杂地表中的应用研究[J]. 大地测量与地球动力学, 2012, 32(4): 120-124 (Guan Zhen, Chen Jianjie, Yu Bohu, et al. Application of GPS Leveling Fitting Based on EGM2008 in Complex Terrain[J]. Journal of Geodesy and Geodynamics, 2012, 32(4): 120-124)
(  0) 0) |
| [12] |
束蝉方, 李斐, 张利明. 基于EGM2008重力场模型的局部高程基准统一[J]. 地球物理学进展, 2011, 26(2): 438-442 (Shu Chanfang, Li Fei, Zhang Liming. Local Height Datum Unification Using EGM2008[J]. Progress in Geophysics, 2011, 26(2): 438-442 DOI:10.3969/j.issn.1004-2903.2011.02.006)
(  0) 0) |
| [13] |
许双安. 基于EGM2008模型的GPS高程转换方法研究[J]. 铁道勘察, 2012, 38(5): 31-34 (Xu Shuang'an. Study on the Method of GPS Height Transformation Using the Earth Gravity Model 2008[J]. Railway Investigation and Surveying, 2012, 38(5): 31-34 DOI:10.3969/j.issn.1672-7479.2012.05.010)
(  0) 0) |
| [14] |
王建忠, 蒋新华, 张广兴. 在小区域内利用EGM2008重力场模型进行GPS高程转换的应用分析[J]. 北京测绘, 2013(1): 79-82 (Wang Jianzhong, Jiang Xinhua, Zhang Guangxing. Analysis on Application of EGM2008 on GPS Height Transformation in the Small Area[J]. Beijing Surveying And Mapping, 2013(1): 79-82 DOI:10.3969/j.issn.1007-3000.2013.01.021)
(  0) 0) |
2. School of Geodesy and Geomatics, Wuhan University, 129 Luoyu Road, Wuhan 430079, China
 2017, Vol. 37
2017, Vol. 37