2. 中国矿业大学环境与测绘学院国土资源与灾害监测国家测绘地理信息局重点实验室,徐州市大学路1号,221116;
3. 浙江省水利河口研究院,杭州市凤起东路50号,310020
高精度形变监测对于结构体的健康维护具有重要意义。由于形变结构体的复杂性及其监测环境的影响,现场采集的形变信号往往是多个信号的混叠,并带有很强的背景噪声及与数据采集系统相关的测量噪声[1]。经验模态分解方法[2](EMD)在处理这类信号时有着明显的优势。作为一种数据驱动的自适应分解方法,可以将复杂的非线性多分量信号分解为易于处理的具有内蕴物理意义的模态分量(IMF)。但是在某些情况下,EMD往往得不到理想的分解结果,出现伪本征模态函数和模态混叠现象[3]。
本文采用EMD的改进方法——完备经验模态分解CEEMD算法解决这个问题。针对分解分量中信号和噪声区分标准不唯一的问题,采用自相关算法,利用白噪声的高斯特性,对模态分量的信号和噪声予以区分。为了最大限度地提取噪声中的有用信号,对首次分解得到的噪声分量再次进行CEEMD自相关降噪处理。通过模拟数据与小波方法进行比较,最后应用于GNSS实测数据处理。
1 CEEMD自相关去噪 1.1 完备经验模态分解的基本原理为克服EMD分解中存在的模态混叠现象,Wu等[4-5]提出集合经验模态分解(EEMD)。但这个方法也引入了其他问题,包括残余噪声和带噪信号不同实现的重构信号可能产生不同的模态数量,IMFs的综合并没有完全重构原始信号。针对EEMD添加白噪声残留较大导致分解不完备,Torres等[6]提出EEMD算法的变体——完备总体经验模态分解(CEEMD),其通过对每一阶分量的分解加入一个特定的白噪声,并且计算一个唯一残差以得到每个模态。该方法能够提供原始信号的精确重构,更好地实现模态频谱分离,并且计算成本更低。
相比于EMD和EEMD,CEEMD不仅解决了模态混叠的问题,而且能够对信号进行精确的重构。对原始信号完成CEEMD分解后,第一个IMF分量包含有原始信号中时间尺度最小的成分。随着IMF阶数的增加,其对应频率成分逐渐降低,余项R则包含频率最低的成分。模态分解准则使得分解余量R为单调函数,其周期大于信号的记录长度。
1.2 CEEMD自相关去噪算法设计根据白噪声的统计特性,其信号序列之间关联性较弱。在自相关函数中,随机噪声在零点处值最大,并在除零点外的其他位置快速衰减,接近于零。对于不含噪的信号序列,序列之间的相关性较强,自相关函数与随机噪声的自相关函数不同,其在零点处具有最大值,在其他位置自相关函数随着时间的变化而变化[7]。本文借助信号和噪声自相关函数的不同特点来判断EMD分解得到的各阶模态分量的含噪量大小,作为判断信号和噪声、分解IMF分量的依据。为了筛选出高频噪声信号中的低频有效信号,充分提取出有用信号,对噪声含量高的低阶模态分量进行重构,选用CEEMD进行分解,通过自相关函数和方差提取出噪声信号中的有用信号,最后将第二次分解处理后提取出的高阶模态分量与第一次分解处理后提取出的基本不含噪声的高阶模态分量进行合成,得到经降噪处理后的信号序列。
本文在详细分析和研究CEEMD和自相关函数两种算法的基础上,针对含噪声信号,提出CEEMD自相关的方法来进行去噪处理,算法整体实现流程如图 1所示。

|
图 1 CEEMD自相关降噪算法流程 Fig. 1 CEEMD correlation denoise algorithm |
由于CEEMD算法是EMD算法的变形体,因此其去噪应用也主要针对高频随机噪声,并且自相关分析方法是利用随机噪声的高斯特性来识别随机噪声,所以基于CEEMD的自相关去噪技术主要是去除信号中的高频随机噪声。
2 实验分析 2.1 模拟实验为了验证CEEMD自相关去噪方法的有效性,首先构造一个简单的形变信号[8],在此模拟信号的基础上,混入一定程度的高斯白噪声序列。合成信号为:
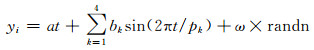
|
(1) |
在本模拟数据中,以较复杂的非线性情况为例,设定at为a(t/1000-2.5)2,其中a=0.2,k=1~4,pk分别为1 200 s、600 s、300 s、150 s。正弦分量的幅值为bk=1,采样间隔Δt=1 s,样本数据为1 000个,合成形变序列和经加噪处理后的信号序列如图 2所示。

|
图 2 合成形变序列及加噪后序列 Fig. 2 Synthetic deformation sequence and additive noise sequence |
含噪信号经CEEMD分解后,通过大量的实验分析,设定筛选的方差阈值为0.030 0。通过计算方差(表 1)可知,前6个模态分量主要为含噪或噪声信号。为了最大限度提取噪声中的有用信号,对前6个模态分量进行重构,再次运用CEEMD自相关方法进行降噪处理,以同样的准则对分解产生的模态分量进行筛选,将分解得到的IMF分量中自相关函数方差大于阈值0.030 0的认为是有用信号。最后将两步处理产生的有用信号序列相加,得到最终经去噪处理后的真实信号序列。
|
|
表 1 各IMF分量归一化自相关函数方差 Tab. 1 Normalized autocorrelation function variance of each IMF |
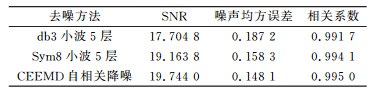
为了验证CEEMD自相关消噪的效果,采用小波分析算法对模拟信号进行去噪处理并与本算法进行效果对比。采用Sym8小波和db3小波(这两种小波方法都具有较好的光滑性)进行5层分解,借助Heurusre进行软阈值消噪。为了能够定量地比较以上3种算法的降噪效果,对经降噪处理后得到的有用信号部分,选用均方误差NRMSE、互相关系数R、信噪比SNR三个指标定量评价消噪效果。
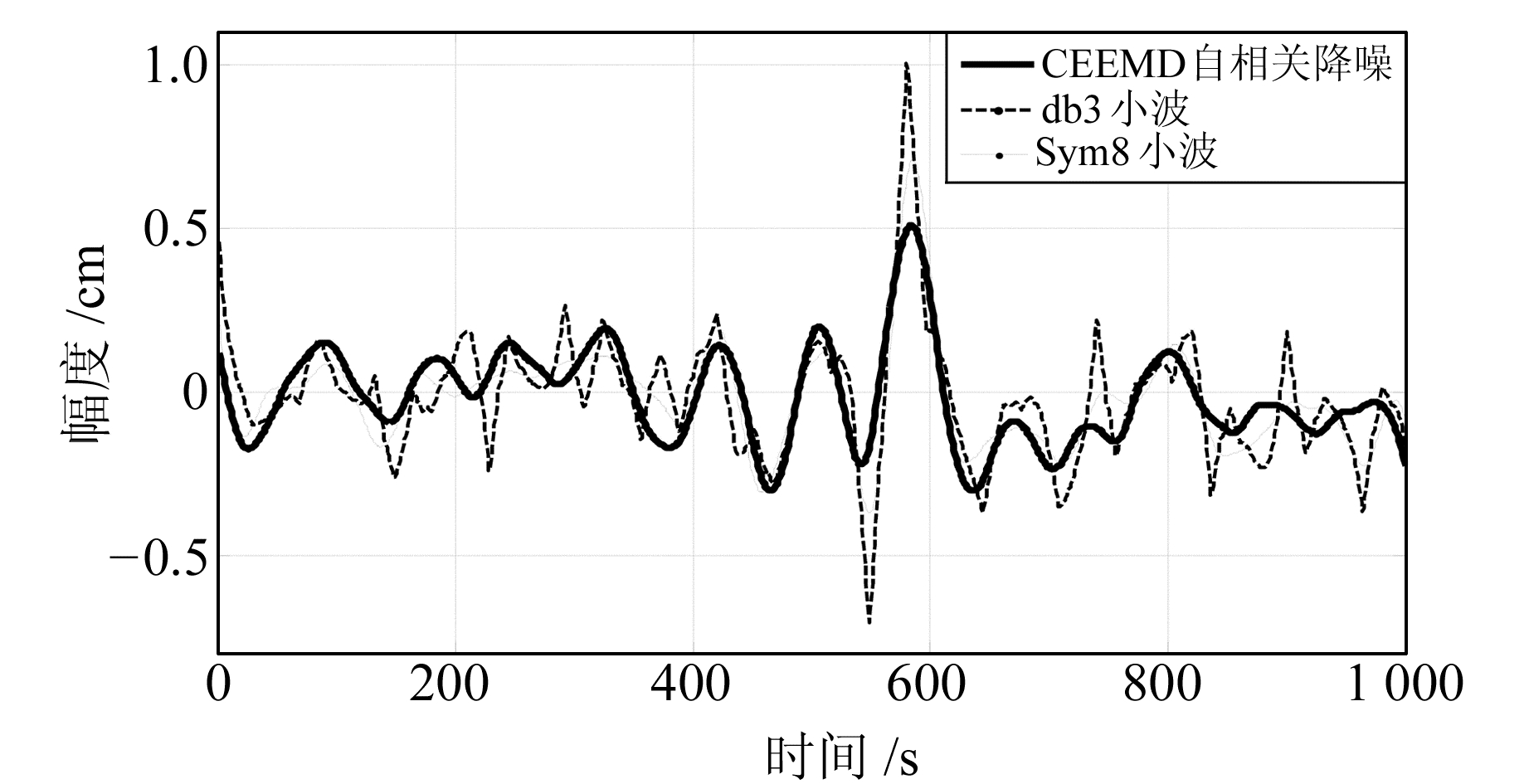
分别比较本方法与上文提出的两种小波方法的去噪效果(图 3)可以看出,本方法得到的重构误差整体上更加平稳。在第600个点附近,两种小波降噪方法产生较大重构误差时,本方法仍能保持较好的稳定性。从表 2的数据中可以得出,经本方法降噪得到的有用信号,与真实信号计算得到的均方根误差最小,相关系数最高,性噪比最大,性能最优。
|
图 3 3种方法消噪后信号重构误差 Fig. 3 The real signal and de-noising signal of three method and error |
|
|
表 2 3种方法降噪效果 Tab. 2 De-noising output signal of three methods |
如图 4所示,在楼顶布设两台南方S86型接收机,一台作为基准站,一台作为移动站。接收机采样频率为1 Hz,高度截止角设置为15°,基线长大约为49 m,采用GPS/BDS双频载波/伪距观测值,在RTKLIB基础上进行开发,对移动站进行单历元双差解算。由于基线距离很短且站间高差很小,电离层、对流层延迟等空间相关误差得到很大程度的削弱。以长时段数据的静态解算作为移动站的真值,通过与动态解算作差求得移动站的形变量,单历元解算得到的变形经过转化得到当地坐标系统的变形分量。

|
图 4 GNSS接收机布设位置及环境 Fig. 4 GNSS receiver layout and environment |
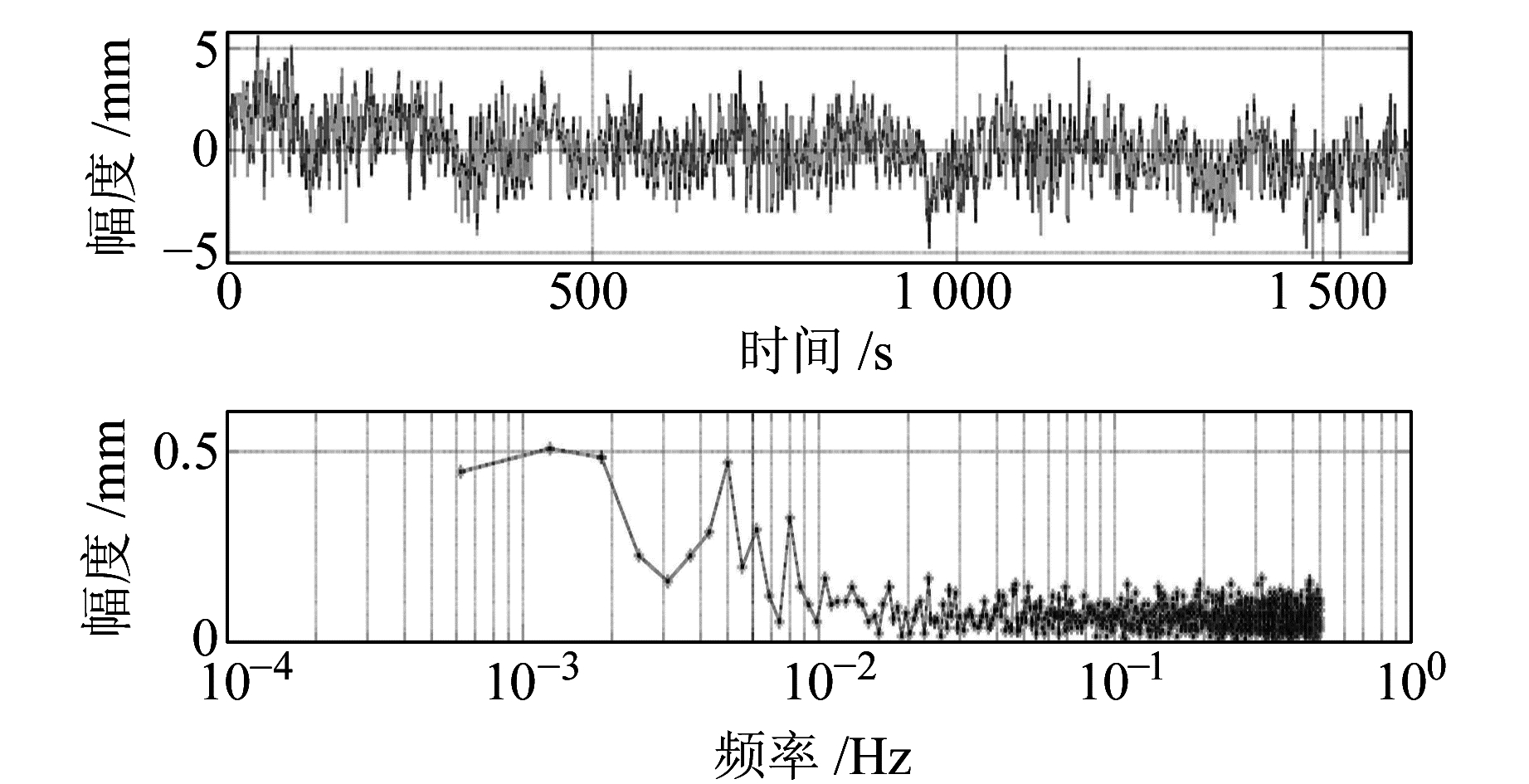
以N方向的时间序列为例进行CEEMD自相关降噪处理,解算得到的时间序列形变量和频谱分析结果如图 5所示。可以从解算结果中看出,站点N方向受到一定程度的高频噪声影响。
|
图 5 站点N方向的时间序列和频谱 Fig. 5 The time series and frequency of the N directions of the site |
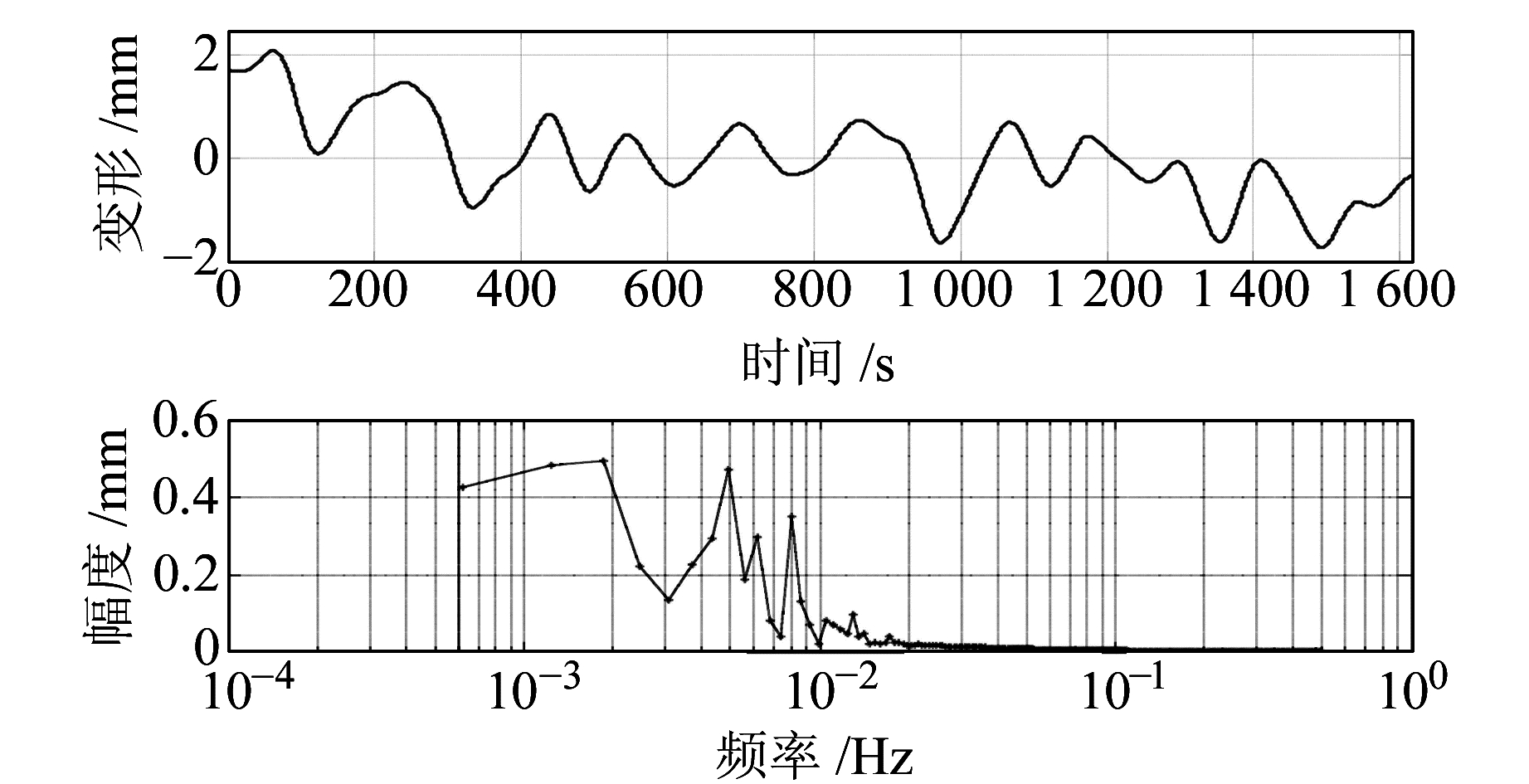
通过多次实验,以方差阈值0.030 0为标准,经去噪处理后得到的真实形变时间序列及频谱如图 6所示。可以看出,本方法在滤除高频噪声的同时,对小幅度的波动信号也有较好的保留效果,能够在保持与原有信号基本一致的同时,将有效信号和随机噪声信号进行分离。经降噪处理后形变幅度为3 mm,而对于本案例中的移动站监测,在短时间内形变量应该接近为0,故认为形变量中存在系统误差的影响。从消噪后得到的真实信号的频谱图(图 6)可以发现,信号序列主要表现为低频率特征。而对于GNSS短基线差分测量来说,基线两端的环境不同,造成多路径误差也不同,不能借助差分方法予以消除[9]。从图 4(b)可以看出,移动站周边有明显的反射物体,能够产生多路径效应,多路径的频率特征[10]满足图 6所示的频谱规律,说明形变序列中的误差为系统误差——多路径误差,所以认为信号降噪处理后得到的序列主要是多路径误差。
|
图 6 降噪后时间序列及频率 Fig. 6 Time series and frequency after de-noising |
本文采用CEEMD来改善模态混叠现象,针对CEEMD分解中噪声信号和有效信号分界点不明确的问题,使用自相关函数进行改进,提出了基于完备经验模态分解的自相关消噪技术。该方法提供了更加可靠的分界点依据,在降噪的同时最大限度地提取有用信号,很好地弥补了EMD降噪的不足。CEEMD是基于EMD算法的,因此具有自适应的基函数分解特性,针对不同的信号数据,都能达到较好的去噪效果。通过仿真实验与实测数据验证显示,本方法在保留信号真实成分的前提下,有效降低了高斯白噪声的含量,可将其应用于GNSS高精度测量中随机噪声的降噪处理。
| [1] |
党星海, 赵丽洁, 孔令杰, 等. 小波分析在GPS振动监测数据中的应用[J]. 大地测量与地球动力学, 2013, 33(2): 147-150 (Dang Xinghai, Zhao Lijie, Kong Lingjie, et al. Application of Wavelet Analysis in GPS Dynamic Deformation Data Processing[J]. Journal of Geodesy and Geodynamics, 2013, 33(2): 147-150)
(  0) 0) |
| [2] |
Huang N E, Shen Z, Long S R, et al. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis[J]. Proceedings of the Royal Society A Mathematical Physical & Engineering Sciences, 1998, 454(1971): 903-995
(  0) 0) |
| [3] |
肖瑛, 殷福亮. 解相关EMD:消除模态混叠的新方法[J]. 振动与冲击, 2015, 34(4): 25-29 (Xiao Ying, Yin Fuliang. Decorrelation EMD: A New Method of Eliminating Mode Mixing[J]. Journal of Vibration and Shock, 2015, 34(4): 25-29)
(  0) 0) |
| [4] |
Wu Z H, Huang N E. Ensemble Empirical Mode Decomposition: A Noise-Assisted Data Analysis Method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41
(  0) 0) |
| [5] |
Wu Z H, Huang N E. A Study of the Characteristics of White Noise Using the Empirical Mode Decomposition Method[J]. Proceedings of the Royal Society A Mathematical Physical & Engineering Sciences, 2004, 460(2046): 1597-1611
(  0) 0) |
| [6] |
Torres M E, Colominas M A, Schlotthauer G, et al. A Complete Ensemble Empirical Mode Decomposition with Adaptive Noise[C].IEEE International Conference on Acoustics, Speech, and Signal Processing, Prague, 2011
(  0) 0) |
| [7] |
席旭刚, 武昊, 罗志增. 基于EMD自相关的表面肌电信号消噪方法[J]. 仪器仪表学报, 2014, 35(11): 2494-2500 (Xi Xugang, Wu Hao, Luo Zhizeng. De-Noising Method of the sEMG Based on EMD Autocorrelation[J]. Chinese Journal of Scientific Instrument, 2014, 35(11): 2494-2500)
(  0) 0) |
| [8] |
张安兵, 张兆江, 高井祥, 等. GPS用于矿区沉陷区地表高精度动态监测的可行性研究[J]. 煤炭学报, 2009, 34(10): 1322-1327 (Zhang Anbing, Zhang Zhaojiang, Gao Jingxiang, et al. Feasibility Study on Mining Surface Subsidence High-Precision Monitoring Using GPS[J]. Journal of China Coal Society, 2009, 34(10): 1322-1327 DOI:10.3321/j.issn:0253-9993.2009.10.005)
(  0) 0) |
| [9] |
戴吾蛟. GPS精密动态变形监测的数据处理理论与方法研究[D].长沙: 中南大学, 2007 (Dai Wujiao. A Study of Data Processing For Precise Dynamic Deformation Monitoring Using GPS[D]. Changsha: Central South University, 2007) http://cdmd.cnki.com.cn/Article/CDMD-10533-2007197868.htm
(  0) 0) |
| [10] |
黄丁发, 丁晓利, 陈永奇, 等. GPS多路径效应影响与结构振动的小波滤波筛分研究[J]. 测绘学报, 2001, 30(1): 36-41 (Huang Dingfa, Ding Xiaoli, Chen Yongqi, et al. Wavelet Filters Based Separation of GPS Multi-Path Effects and Engineering Structure Vibrations[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(1): 36-41 DOI:10.3321/j.issn:1001-1595.2001.01.008)
(  0) 0) |
2. Key Laboratory for Land Environment and Disaster Monitoring of NASMG, School of Evironment Science and Spatial Informatics, China University of Mining & Technoloty, 1 Daxue Road, Xuzhou 221116, China;
3. Zhejiang Institute of Hydraulics & Estuary, 50 East-Fengqi Road, Hangzhou 310020, China
 2017, Vol. 37
2017, Vol. 37