国际地球参考框架ITRF[1-4]的综合数据处理方式主要分两种:一是采用相同的常数和误差改正模型,用同一数据处理软件统一处理GNSS/VLBI/SLR/DORIS观测数据,对软件和数据处理技术要求甚高,主要由IERS(international earth rotation service)组织的DGFI(deutsches geodtisches forschungsinstitut)和IGN(institute géographique national)机构负责解算;二是基于IGS提出的数据解的标准格式SINEX(solution independent exchange)文件的组合,输入数据为处理后的测站坐标、速度及其协方差阵等信息,并根据不同技术特点引入约束条件,解算参考框架[5]。徐天河等[6]和Hu等[7]建立了各技术观测量与综合解间的七参数转换关系,并将基准定义的条件作为约束方程,根据综合解的观测量和基准定义方式的不同提出了3种综合解算方案,并证明这3种处理方式在参数的设置、随机模型、先验约束等因素相同的情况下,用SINEX文件给出的成果代替原始观测量参与平差是完全可行的,且其最终结果是等价的,但并未顾及坐标速度和并址站归心基线等信息。
并址站归心基线作为连接ITRF中GNSS/VLBI/SLR/DORIS观测技术的主要约束条件,对于解算ITRF必不可少[1-2]。根据ITRF网站公布的并址站归心基线成果,ITRF2008解算中所用到的并址站归心基线以SINEX文件的形式给出,SINEX文件中给出了基线两个端点的单位权方差因子
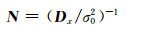
|
(1) |
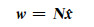
|
(2) |
同样,ITRF2008解算前也需要利用SINEX文件恢复GNSS、VLBI和SLR站各自的法方程,再与并址站的法方程叠加后进行平差[8]。通常,基线向量指的是一条基线上两个端点的坐标差。在已有误差方程中增加新的观测量时,一般以虚拟观测量或约束条件的方式引入,本文是将并址站归心基线作为虚拟观测量引入至ITRF2008中。目前在ITRF2008的解算中,已经用到了陆态网络中北京GNSS/SLR站、武汉GNSS/SLR站和上海GNSS/VLBI/SLR站,而长春GNSS/SLR站、昆明GNSS/VLBI/SLR站和乌鲁木齐GNSS/VLBI站未被采用。因此,本文将这3个新的并址站引入2011年观测得到的归心基线及其方差协方差阵,分析其对ITRF2008中站点坐标及其速度的影响。
1 引入新的归心基线的ITRF综合解算公式ITRF是利用处理后的GNSS/VLBI/SLR/DORIS 4类技术的测站坐标、速度及其协方差阵等信息,并根据不同技术特点引入约束条件,解算组合后的参考框架。组合参考框架c与单个坐标框架s之间关于站坐标及其速度的转换方程为[2]:
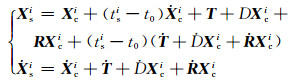
|
(3) |
式中,Xsi和Ẋsi表示单个技术坐标框架s在计算历元tsi时测站i的位置和速度,Xci和Ẋc i表示组合框架c在参考历元t0的位置和速度,D、T和R为两类坐标框架之间的尺度参数、平移向量和旋转矩阵,Ḋ、Ṫ和Ṙ为其随时间的变化率。
令xs=(Xsi, Ẋsi)T,xc=(Ẋci, Ẋci)T,φ =(D, Ḋ, T, Ṫ, R, Ṙ)T,式(3)可写为:
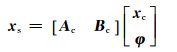
|
(4) |
式中,Ac和Bc为xc和φ的系数阵。其中,

|
设(xG, xV, x S)和(xcG, xcV, x cs)为GNSS、VLBI和SLR站的独立解和在组合框架c中的坐标及其速度向量,φcG、φcV和φcS为组合框架c与GNSS、VLBI和SLR单个坐标系统之间的转换参数及其速度向量。展开式(4)可列出GNSS、VLBI和SLR单个坐标系统与组合框架c的误差方程为:
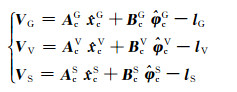
|
(5) |
式中,

式(5)可以综合表示为:

|
(6) |
其中,
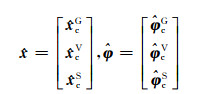
|
(7) |
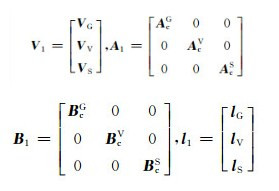
|
(8) |
并址站归心基线向量误差方程可以表示为:
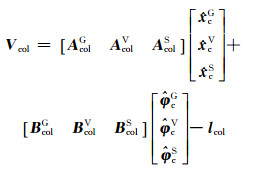
|
(9) |
式中,Vcol为并址站空间归心基线向量改正数,lcol为其常数项,(AcolG, AcolV AcolS)为GNSS、VLBI和SLR并址站在组合框架c中的未知坐标及速度向量改正数的系数矩阵;(BcolG, BcolV, BcolS)为并址站坐标框架与组合框架c之间的转换参数及其速率向量改正数的系数矩阵。
需要说明的是,并址站归心基线与组合框架c之间的转换只需要8个转换参数,包括1个尺度参数和3个旋转角度及其变率。
式(9)可以综合为:
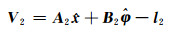
|
(10) |
式中,
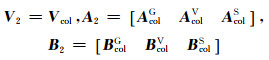
|
(11) |
原点、尺度和定向及其随时间演变的基准定义可作为约束条件引入误差方程中。在ITRF2008中原点相对于SLR时间序列平移及平移变化率为零[2],平移向量及速率可以表示为:
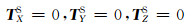
|
(12) |

|
(13) |
式中,(TXS, TYS, TZS)为SLR技术解与组合框架c之间的平移向量,(ṪXS, ṪYS, ṪZS)为其平移向量变化率。
ITRF2008中尺度相对于VLBI和SLR时间序列的平均尺度及尺度变化率为零[2],即组合框架c的尺度采用组合框架c与VLBI和SLR之间尺度因子的加权平均:
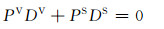
|
(14) |
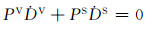
|
(15) |
式中,PV和PS为VLBI和SLR技术解的权;DV和DS为VLBI和SLR技术解与组合框架c之间的尺度因子,ḊV和ḊS为其尺度因子变化率。
式(12)~(15)经线性化后可表示为:
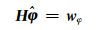
|
(16) |
式中,H为约束方程中未知参数向量系数矩阵,wφ为约束方程的常数项。
式(16)联立式(6)、式(10)得:
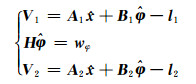
|
(17) |
令式(17)中第1式的方差阵为Σ1,第3式的方差阵为Σ2,根据最小二乘原理可求得式(17)的法方程为:

|
(18) |
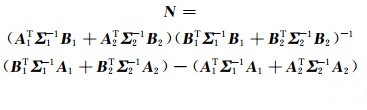
|
(19) |
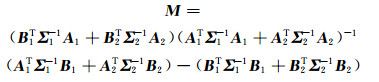
|
(20) |
根据式(18),得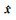
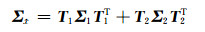
|
(21) |
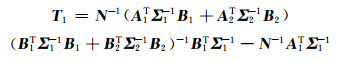
|
(22) |
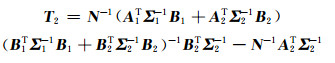
|
(23) |
根据式(18)和式(21)可以获取在ITRF中引入新的归心基线后站点的坐标及其速度的参数估值及精度。
当不包含并址站归心基线,即不引入式(17)的第3式时,A2=0,B2=0,式(18)变为:
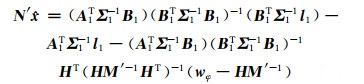
|
(24) |
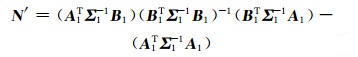
|
(25) |
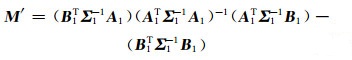
|
(26) |
对比式(24)和式(18)可以看出,当引入并址站归心基线的误差方程时,在原有的法方程和常数项基础上再次进行叠加即可。
2 计算结果与分析由于目前ITRF网站很难获取到GNSS、VLBI、SLR和SLR单个观测技术的坐标及其速度的时间序列,因此本文利用ITRF2008站点的SINEX文件(ITRF2008-TRF.SNX)中给出的点坐标、速度值及其方差协方差阵
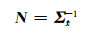
|
(27) |
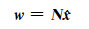
|
(28) |
式中,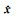
如前所示,长春GNSS/SLR站、昆明GNSS/SLR站、乌鲁木齐GNSS/VLBI站的归心基线在ITRF2008解算中并未采用,加入这些并址站基线,对框架坐标必定产生影响。由于并址站基线是相对量,增加3个并址站基线对转换参数的影响比较小。忽略其影响后,假定这3个并址站在ITRF2008中的归心基线向量分别为Δxchan=(ΔXchan, ΔYchan, ΔZchan)、Δxkunm=(ΔXkunm, ΔYkunm, ΔZkunm)、Δxurum=(ΔXurum, ΔYurum, ΔZurum),则在ITRF2008中引入新的归心基线的误差方程为:

|
(29) |
式(29)可简化为:
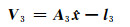
|
(30) |
式中,A3为3个并址站归心基线所构成的系数矩阵。
组合式(28)和式(30)得:
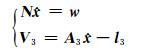
|
(31) |
利用法方程和常数项的叠加,式(31)中的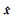
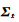
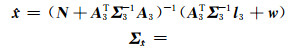
|
(32) |
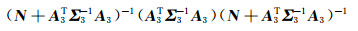
|
(33) |
式中,Σ3为新的并址站归心基线的方差协方差矩阵。
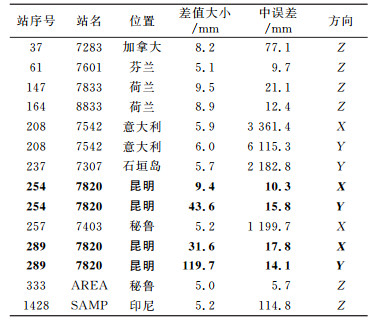
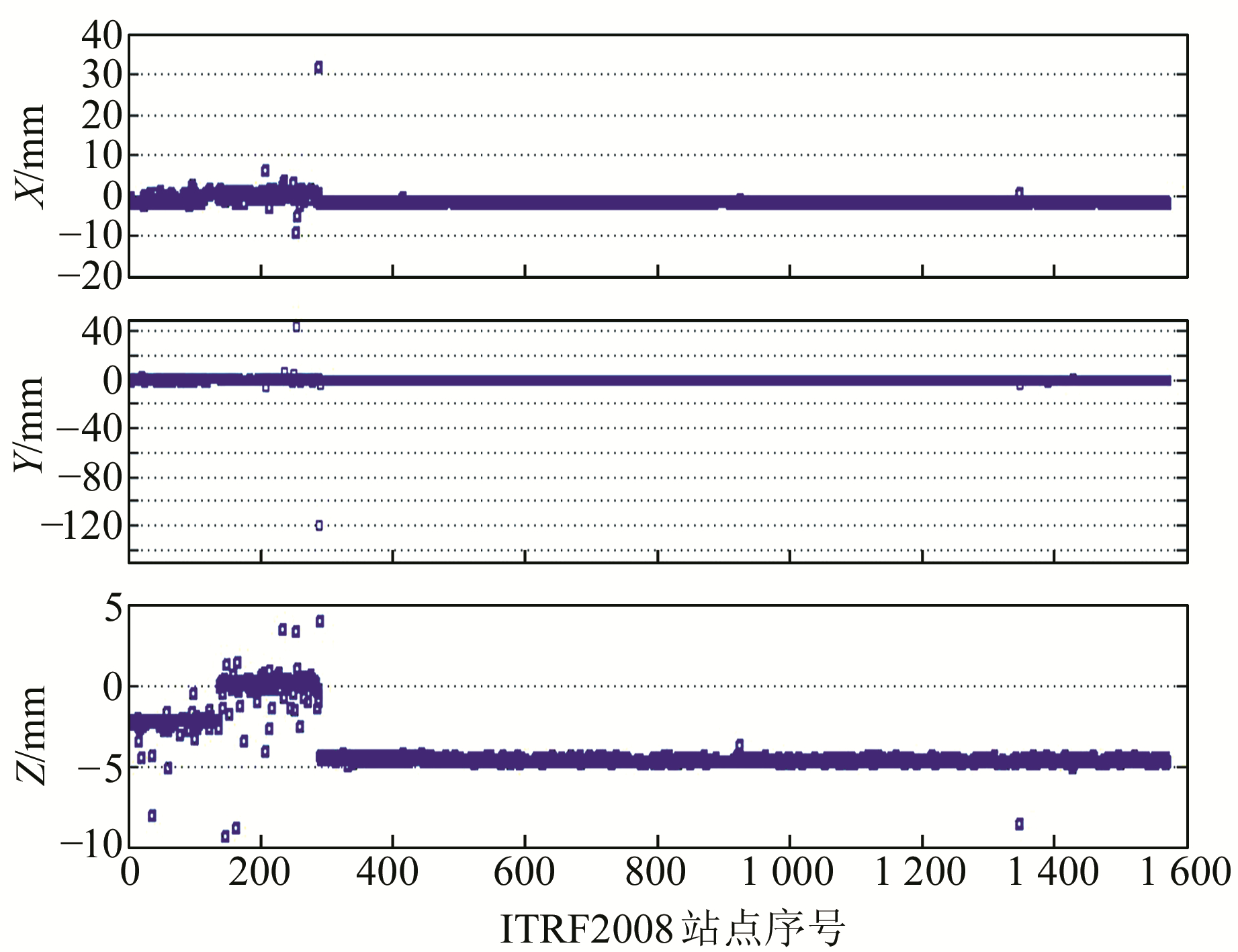
Gong等[9]解算出了“陆态网络”中长春GNSS/SLR站、昆明GNSS/SLR站和乌鲁木齐GNSS/VLBI站在ITRF2008中的归心基线及其方差协方差阵[9],与ITRF2008相比,3个并址站的差值分别为-34.1 mm、94.1 mm和-0.7 mm。引入这3个并址站归心基线及其协方差阵,利用式(32)对ITRF2008重新进行解算,并与ITRF2008的成果相比较发现,在ITRF2008的1 572个站点(包含重复站点)中,X、Y、Z3个方向的差值具体如图 1所示(图中站点的序号与ITRF中给出的站点序号一致,根据序号可以找到相应的站点编码)。其中,X、Y、Z方向差值的平均值分别为1.9 mm、0.6 mm、4.1 mm,X、Y、Z 3个方向差值最大分别为31.6 mm、119.7 mm、9.5 mm,所有站点的坐标差值都小于50 mm,其中3个方向差值均小于10 mm的站点的个数分别为1 570个、1 569个、1 572个。可见,绝大多数站点的坐标差值小于10 mm,总体上在Z方向的影响比X和Y方向的大。
|
图 1 站点在X、Y、Z方向的坐标差值 Fig. 1 Differences of sites in the X, Y, Z directions |
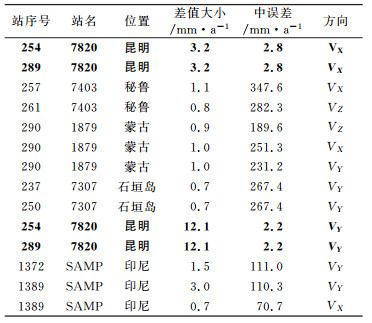
X、Y、Z 3个方向的坐标速度差值如图 2所示。其中,X、Y、Z方向坐标速度差值的平均值分别为0.03 mm/a、0.03 mm/a、0.04 mm/a,3个方向速度差值最大值分别为-3.71 mm/a、12.10 mm/a、1.11 mm/a,差值小于1 mm/a的站点个数分别为1 568个、1 566个、1 570个。因此,绝大多数站点的坐标速度差值小于1 mm/a。

|
图 2 站点在X、Y、Z方向的坐标速度差值 Fig. 2 Velocity differences of sites in the X, Y, Z directions |
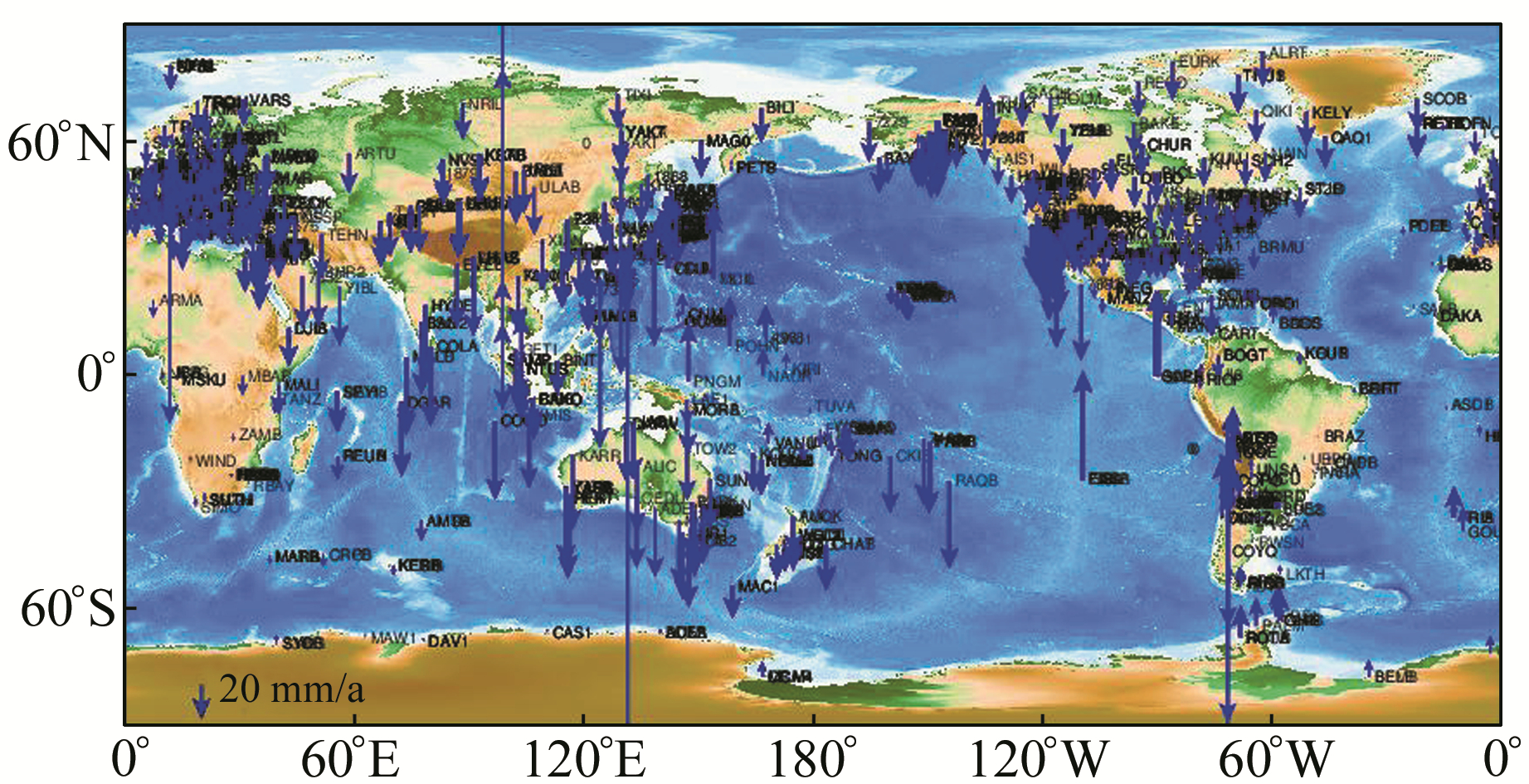
在绘制ITRF2008中站点速度图时,需要将空间直角坐标速度值换算为站心坐标速度值。图 3和图 4给出了在ITRF2008中引入陆态网络3个并址站归心基线后得到的速度场与ITRF2008速度场在水平方向和垂直方向的比较。其中,图 3和图 4中红色线条代表引入新的归心基线后与ITRF2008相比在大小和方向上不同的站点速度矢量,蓝色线条代表与ITRF2008速度场相一致。可以看出,绝大多数站点在水平方向和垂直方向的速度场与ITRF2008速度场一致。

|
图 3 ITRF2008中站点的速度场在水平方向的比较 Fig. 3 Comparison of velocity field in ITRF2008 sites in the horizontal direction |
|
图 4 ITRF2008中站点的速度场在垂直方向的比较 Fig. 4 Comparison of velocity fields in ITRF2008 sites in the vertical direction |
分析以上结果可以得出:
1) 在ITRF2008解算中引入这3个并址站归心基线后,对ITRF2008坐标的影响大部分小于10 mm,对速度的影响大部分小于1 mm/a。
2) 从图 1可以看出,加入3个并址站的归心基线后,Z方向的变动范围为-9.5~3.8 mm,且1 482个台站在Z方向的差值均为负值,平均约为-6 mm,即会造成Z方向变动平均约为-6 mm。
3) 从图 1和图 2可以看出,少部分台站变化比较剧烈,为此我们将坐标差值大于5 mm和坐标速度差值大于1 mm/a台站的位置、中误差和差值分别进行统计,如表 1和表 2所示。可以看出,坐标最大中误差超过6 m,最大速度中误差为282.2 mm/a。分析后发现,这些台站有两个特点:一是位于离中国比较远且中误差较大的国家和地区,如意大利、芬兰、秘鲁、加拿大、印尼等国家或地区;二是离中国虽近但中误差较大的地方,如蒙古和石垣岛等。这表明差值的大小主要是跟中误差有关,其原因主要在于在ITRF2008中对个别站点之间增加了约束,会对整体框架产生影响,相当于对已有的坐标框架进行了转换。根据坐标转换的实质,离转换中心越远误差越大,公共点的微小变化对转换点的影响也越大。但有些离中国很远且中误差很小的站点基本不受影响,这是因为在ITRF2008中引入的这3个并址站,站数少且基线长度短(最大约为80 m),与ITRF2008全球范围的基线长度相比,其影响非常有限。此外,由于昆明SLR的并址站基线与ITRF2008差值在94.1 mm,因此平差后能反映在3个残差向量上(表 1和表 2中以加粗表示)。
|
|
表 1 坐标差值大于5 mm的站点 Tab. 1 Sites of coordinate difference greater than 5 mm |
|
|
表 2 坐标速度差值大于1 mm/a的站点 Tab. 2 Sites of coordinate velocity difference greater than 1 mm/a |
4) 根据ITRF网站公布的站点速度值(ITRF2008-TRF.snx)文件可知,站点的坐标速度值最大超过100 mm,而从图 2中可以看出,加入陆态网络3个并址站对速度的影响绝大多数站点都小于1 mm/a,因此速度的量值基本一致(如图 3和图 4),但由于速度值有方向,本文计算的水平方向与ITRF2008给出的水平方向除个别站点(红线表示)有所不同外,其他站点水平移动的方向基本一致,而垂直方向完全一致。
3 结语本文详细分析了在ITRF2008中引入陆态网络2011年得到的3个并址站(长春、昆明和乌鲁木齐)归心基线及其协方差阵后对ITRF2008的影响,得到以下结论:
1) 对ITRF2008站点坐标及其速度的影响均较小,且该影响的大小主要与ITRF2008站点坐标和速度的中误差大小有关。
2) 绝大多数站点3个方向的坐标差值小于10 mm,其中最大差值为119.7 mm。
3) 绝大多数站点3个方向的坐标速度差值小于1 mm/a,其中最大差值为12.1 mm/a。
| [1] |
Altamimi Z, Collilieux X, Legrand J, et al. ITRF2005: A New Release of the International Terrestrial Reference Frame Based on Time Series of Station Positions and Earth Orientation Parameters[J]. Journal of Geophysical Research: Solid Earth, 2007, 112(B9): 1978-2012
(  0) 0) |
| [2] |
Altamimi Z, Collilieux X, Métivier L. ITRF2008: An Improved Solution of the International Terrestrial Reference Frame[J]. Journal of Geodesy, 2011, 85(8): 457-473 DOI:10.1007/s00190-011-0444-4
(  0) 0) |
| [3] |
Böckmann S, Artz T, Nothnagel A. VLBI Terrestrial Reference Frame Contributions to ITRF2008[J]. Journal of Geodesy, 2010, 84(3): 201-219 DOI:10.1007/s00190-009-0357-7
(  0) 0) |
| [4] |
Altamimi Z, Collilieux X. IGS Contribution to the ITRF[J]. Journal of Geodesy, 2009, 83: 375-383 DOI:10.1007/s00190-008-0294-x
(  0) 0) |
| [5] |
刘经南, 魏娜, 施闯. 国际地球参考框架(ITRF)的研究现状及展望[J]. 自然杂志, 2013, 35(4): 243-250 (Liu Jingnan, Wei Na, Shi Chuang. Status and Prospects of the International Terrestrial Reference Frame (ITRF)[J]. Chinese Journal of Nature, 2013, 35(4): 243-250)
(  0) 0) |
| [6] |
徐天河, 杨元喜. VLBI、SLR、GNSS综合数据处理方案研究[J]. 测绘工程, 2002, 12(4): 7-11 (Xu Tianhe, Yang Yuanxi. The Research on the Schemes of Combination Adjustment of VLBI、SLR and GPS Data[J]. Engineering of Surveying and Mapping, 2002, 12(4): 7-11 DOI:10.3969/j.issn.1006-7949.2002.04.002)
(  0) 0) |
| [7] |
Hu X G, Liao X H, Huang C. Data Weighting and Solution Assessment in Combination[J]. Journal of Geodesy, 1999, 73(8): 391-397 DOI:10.1007/s001900050258
(  0) 0) |
| [8] |
姚宜斌. GPS精密定位定轨后处理[M]. 北京: 测绘出版社, 2008 (Yao Yibin. Post-Processing on GPS Precise Positioning and Orbit Determination[M]. Beijing: Surveying and Mapping Press, 2008)
(  0) 0) |
| [9] |
Gong X Q, Shen Y Z, Wang J X, et al. Surveying Colocated GNSS, VLBI, and SLR Stations in China[J]. Journal of Surveying Engineering, 2013, 140(1): 28-34
(  0) 0) |
 2017, Vol. 37
2017, Vol. 37