2. 地球空间信息技术协同创新中心, 武汉市珞喻路129号, 430079
桥梁挠度测量是铁路桥梁检测的重要组成部分,是其安全性评价的一项重要指标。铁路桥梁的挠度与桥梁的承载能力及抵御地震等动荷载的能力有密切关系。因此,铁路桥梁动、静挠度测量方法的研究和仪器设备的开发研制对于桥梁承载能力的检测和桥梁的防震减灾有着重要意义[1]。桥梁挠度测量主要是对桥跨在恒载和动载情况下的挠度进行测量。因此在桥梁检测、危桥改造以及新桥验收等方面都需要准确测量桥梁的静、动态挠度值。随着桥梁健康监测技术的进步,人们研究了许多挠度测量的方法,常用的方法主要有精密水准法、挠度仪、百分表、连通管法、GPS观测法、测量机器人法、激光图像测量法等[2-4]。目前广泛应用于大型桥梁挠度测量且具有一定代表性的包括测量机器人、水准测量和连通管等。测量机器人外业测量简单、精度高但测点稀;水准测量精度高、点位密,但外业工作量大、周期长;连通管精度高、自动化、点位密,但前期安装和后期维护的成本高[5],而且这些都是接触式的测量模式。
地面三维激光扫描技术采用新的数据获取模式,具有现有测量手段所不具备的优点,以非接触式、自动化、高精度、测程大的特点快速获取高精度、高密度的三维点云数据。通过对点云数据的处理与分析,可以快速得到桥梁的几何信息,实现对桥梁挠度的测量。
1 数据采集某桥通车前的静态荷载实验在凌晨前后进行,天气状况良好。采用RIEGL VZ400地面三维激光扫描仪对桥体进行扫描测量。由于桥梁静态荷载对于测量而言,是一个动态过程,时间较短,不能采用多站拼接的方式测量整个桥体,只能一站测量。同时也受现场条件的限制,激光扫描仪只能架设在堤岸上,虽然扫描有效范围有400余m,但因桥塔遮挡和仪器距桥塔较远,使得扫描的桥底面有效长度只有120余m。共进行了6个时刻的扫描:时刻1和时刻2是在加载前的两次扫描,时刻3是在半静态荷载下的测量,时刻4是在满荷载下的测量,时刻5和时刻6是荷载撤离后桥梁又处于空荷载后的两次测量,图 1为时刻1的扫描点云数据。为了方便后面的计算以及变形表达,本文根据扫描的点云数据,人工获取特征点,将扫描仪坐标系转换到以桥塔墩与桥面交点为坐标原点O、以桥轴线为X轴方向、以天顶方向作为Z轴方向、Y轴由右手法则确定的局部三维直角坐标系(图 1)。由于被桥墩遮挡,因此实际分析的桥底点云从距原点100 m开始。

|
图 1 时刻1的扫描点云数据 Fig. 1 Scanning point cloud data of time 1 |
在静态荷载测试中,桥面会随着荷载的变化而发生挠度变化,所以根据桥面底部数据就可以求得桥梁挠度的变化。本文选取桥面底部箱梁(图 2(a))的扫描点云数据,通过计算各箱梁在不同时刻的位置变化来确定桥面挠度。图 2(b)为时刻1(黑色点)与时刻3(灰色点)提取的桥梁底部箱梁扫描数据在局部坐标系下的对比。

|
图 2 桥底照片和两个时刻的扫描点云 Fig. 2 Photo of bridge's bottom and its point clouds on two times |
为了得到桥面的挠度变化,需要计算桥面底部各箱梁在垂直方向的形变。由于两次扫描测量点的不可重复性,即在点云中不能分辨同名变形点,因而不能直接获取形变[6],而需要通过对点云的处理来获取同名变形监测点。本文根据桥梁结构特征和点云特征,采用以下两种方法获取同名点并进行变形计算与比较。
2.2 方法1:基于RANSAC算法与最小二乘拟合的挠度计算RANSAC(random sample consensus)算法即随机采样一致性算法,是一种应用极为广泛的鲁棒模型估计算法。其基本假设是样本中包含正确数据,也包含异常数据,即数据集中含有噪声,并假设给定一组正确的数据,可以计算出符合这些数据的模型参数。其优点是稳定、可靠、精度高,对噪声和特征点提取不准确有很好的承受能力,鲁棒性强,同时具有较好的剔除误匹配点的能力[7]。
桥面底部箱梁侧面的扫描点云是一个窄带状条纹,含有许多杂点,手工难以消除。要将其拟合成为一条空间直线,先通过RANSAC算法过滤掉杂点,再通过最小二乘的方法将RANSAC算法处理后的每条箱梁扫描数据都拟合成一条空间直线方程[8]:
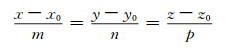
|
(1) |
式中,m、n、p为空间直线的方向分量;(x0, y0, z0)为空间直线经过的某一点,一般是参与拟合点的重心。
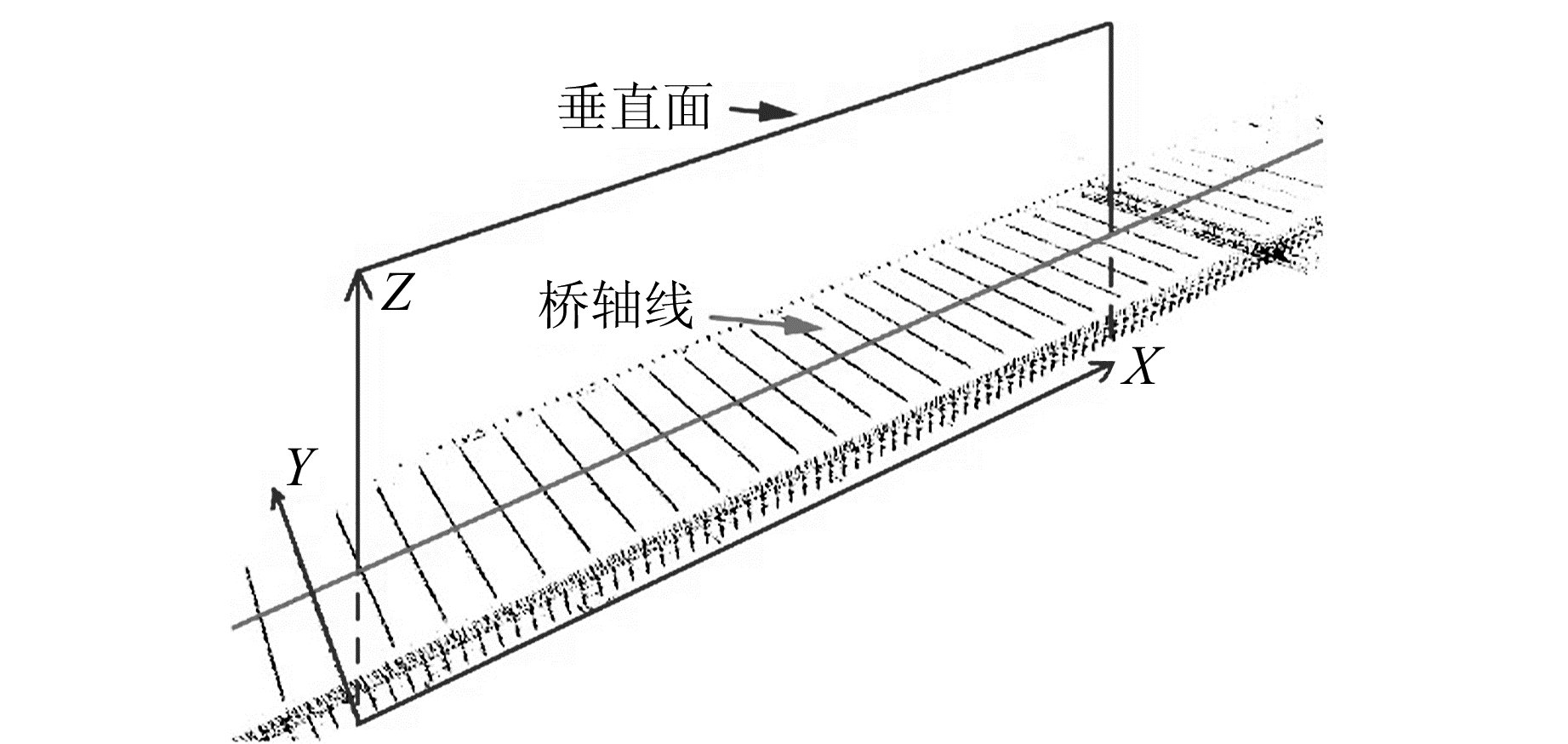
这样,每个底部箱梁都有一条拟合的空间直线方程。为了获得桥轴线的挠度,先确定一个经过桥轴线且垂直于桥面的平面,该平面与各条空间直线的交点,就构成了桥面挠度的变化点(图 3)。若已知平面为y=yM,则代入式(1)可以得到任一条线与该平面的交点坐标计算公式:
|
图 3 方法1获取变形点示意图 Fig. 3 Deformation points schematic diagram by method 1 |

|
(2) |
重心法适合处理形状不规则但具有一定特征的小块点云。具体处理过程为:根据被测物体的表面特征,人工或者自动(如依照法线方向或者曲率变化)分割出特征小块的边界,过滤后得到特征小块点云;将每块特征点云的坐标取平均得重心坐标。如果将每块特征点云看成是一个监测点,则该重心坐标即为监测点坐标。采用相同方式,得到不同期的监测点坐标,进而得到监测点的位移[9]。
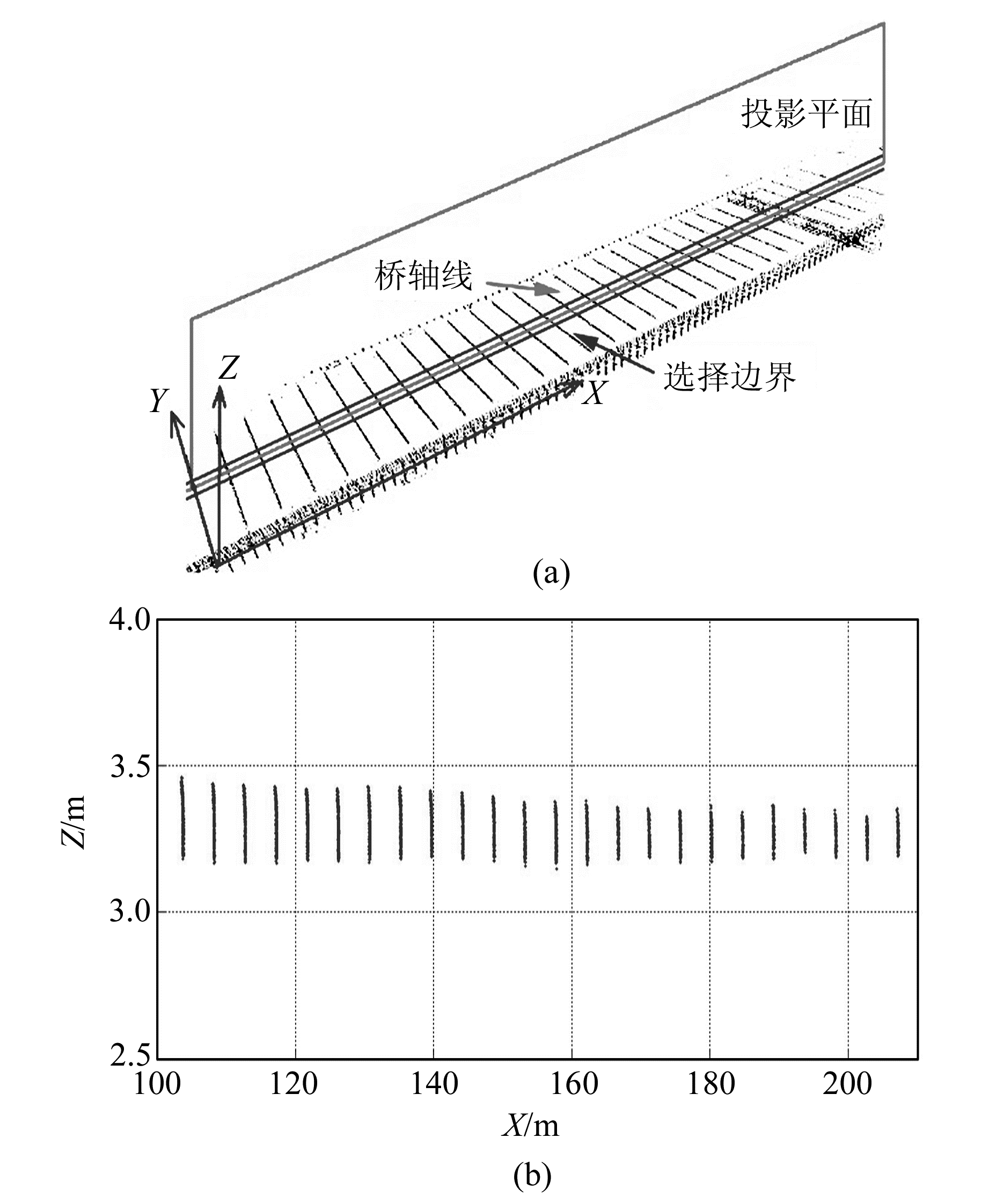
桥面底部箱梁与桥轴线的交点可以看作是桥轴线挠度变化的监测点,由于桥面底部箱梁侧面的扫描点云是一个窄带状条纹,形状不规则。为了得到监测点,先确定一个过桥轴线的垂直平面y=yM(图 4(a)),将该平面两侧2 m范围的点云沿平面法线方向投影到其上面(图 4(b)),作为每条箱梁的特征小块点云,计算其重心坐标:
|
图 4 投影法获取变形点示意图 Fig. 4 Sketch of deformation points by projection |
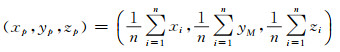
|
(3) |
式中,(xi, zi)(i=1, 2, …, n)为投影后的点云坐标,(xp, yp, zp)为投影后点云数据的重心坐标。通过计算不同时刻监测点的点云数据的重心坐标的变化,确定桥面的挠度变化。
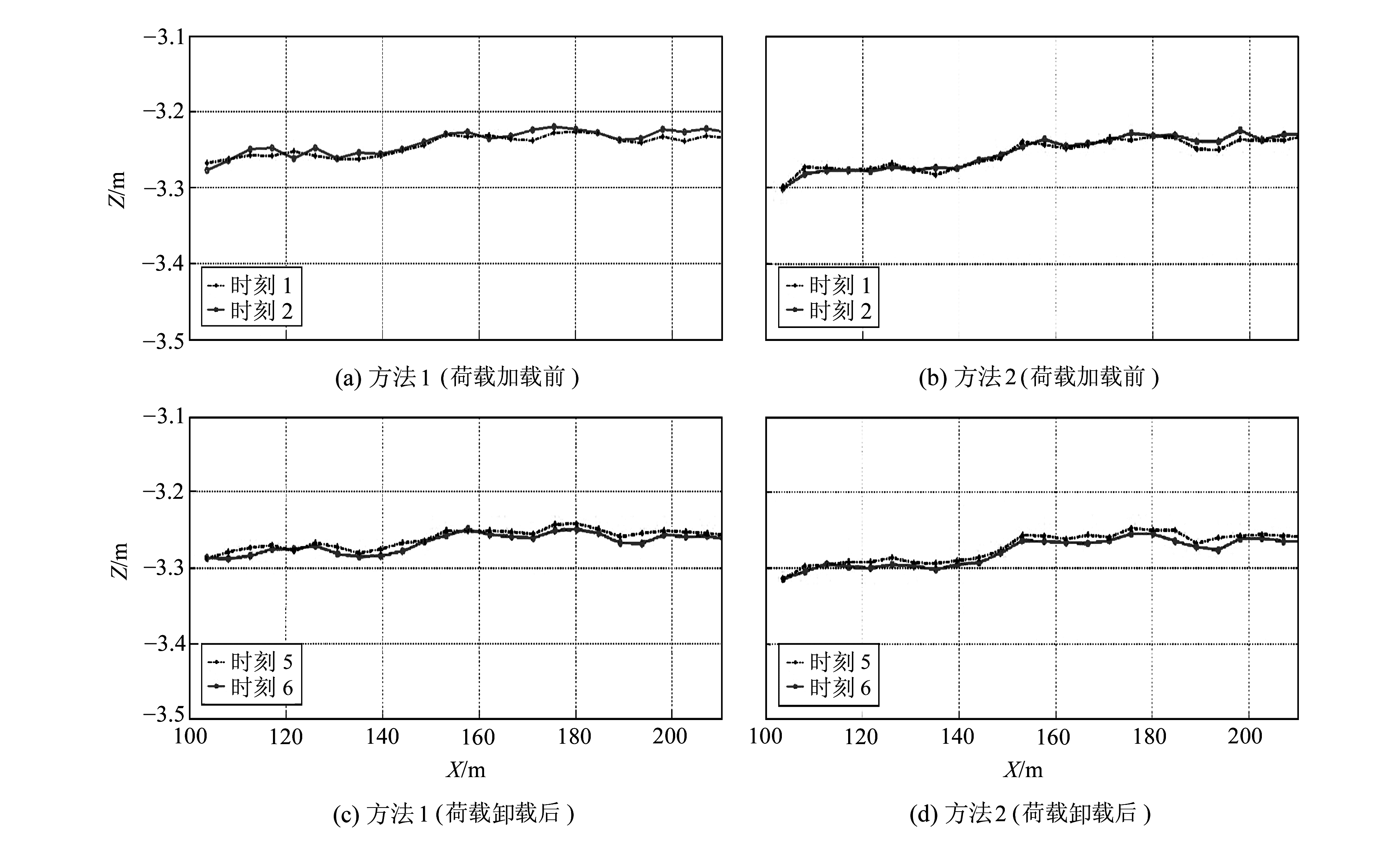
3 实验结果分析本次实验总共测量了6个时刻的数据。为了确定三维激光扫描技术在桥梁挠度测量中的测量精度,利用该桥梁静态荷载试验加载前的两组数据(时刻1与时刻2)中的25条箱梁数据,分别应用方法1与方法2计算出其实际状态(图 5(a)、(b))。利用移去所有荷载后的两组数据(时刻5与时刻6)中相同的25条箱梁数据,分别应用方法1与方法2计算出其实际状态(图 5(c)、(d))。由图 5可以看出,两个相邻时刻的计算结果吻合很好,而且桥面在加载试验结束后没有发生明显变化。
|
图 5 两类无荷载状态下两种计算方法结果的对比 Fig. 5 Comparison between results of two processing methods in two zero-load states |
因扫描时间以及两次扫描间隔很短,而且桥面上没有荷载变化,理论上讲可认为桥梁没有变形,这样,同一点在两个时刻的坐标之差的中误差基本可以反映此次变形测量精度。针对时刻1-时刻2和时刻5-时刻6,分别计算两种方法对应的变形中误差,结果显示,方法1在荷载加载前和荷载移去后的变形测量中误差分别为±9.4 mm和±7.1 mm;方法2在荷载加载前和荷载移去后的变形测量中误差分别为±11.4 mm和±8.9 mm。两种方法精度相近,但方法1的精度略高。
对时刻3和时刻4的数据按照方法1和方法2处理后,减去时刻1和时刻2的平均值,得到桥梁挠度变化曲线(图 6(a)、(b))。

|
图 6 桥梁不同荷载下不同处理方法的挠度曲线 Fig. 6 The deflection curve of bridge under different loads by different data processing |
由图 6可以看出,两种挠度测量方法的计算结果吻合度高,可以相互验证,所得的桥面挠度曲线符合实际状态。因此结合点云的实际,本文采用的这两种数据处理方法较为合理,可用于处理基于三维激光扫描的桥梁挠度测量数据。
4 结语在本次试验中,由于受地形条件的限制,扫描仪距桥塔墩约230 m,同时受桥塔遮挡,故只测到桥底的一部分(120多m),而扫描的桥底最远处距仪器近400 m。本次试验与计算结果表明,采用合适的设备和数据处理方法,发挥扫描测点数据多的优势,在400 m距离内,其变形测量精度可达1 cm左右,验证了三维激光扫描技术在桥梁变形监测中的可行性。因此,充分利用地面三维激光扫描测量技术所具有的长距离、非接触、数据量大的优势,可快速、准确、全面地获得桥梁几何形态和变形信息,为桥梁的安全状态分析提供科学依据。
但也应该注意到,由于地面三维激光扫描采用了无接触测量技术,其测量精度受到多种因素的影响。在点云处理时,需要依据监测表面情况采取有针对性的数据处理方法。三维激光扫描监测桥梁挠度变形的方法,是对现有测量技术的一种补充。相对于测量机器人、水准测量技术等,它在测量精度上和数据处理技术上仍有不足。因此在实际应用时,与其他技术手段相结合是非常必要的。
| [1] |
齐法琳, 孙宁. 铁路桥梁动力学[M]. 北京: 科学技术出版社, 2007 (Qi Falin, Sun Ning. Dynamics of Railway Bridges[M]. Beijing: Science and Technology of China Press, 2007)
(  0) 0) |
| [2] |
吕长荣, 卓秋林, 徐嵩基. 智能全站仪在大型桥梁挠度观测中的应用[J]. 山东交通学院学报, 2009, 17(2): 50-55 (Lü Changrong, Zhuo Qiulin, Xu Songji. Application of Intelligent Total Station in Measuring Large Bridge's Deformation Observation[J]. Journal of Shandong Jiaotong University, 2009, 17(2): 50-55 DOI:10.3969/j.issn.1672-0032.2009.02.012)
(  0) 0) |
| [3] |
曹诗荣. 大型桥梁挠度变形监测方法的分析[J]. 地理空间信息, 2010, 8(2): 137-139 (Cao Shirong. Methods for Measuring Bridge Deflections[J]. Geospatial Information, 2010, 8(2): 137-139 DOI:10.3969/j.issn.1672-4623.2010.02.045)
(  0) 0) |
| [4] |
廖中平, 华赛男, 刘宁, 等. R8 GNSS、TCA2003和SPRINTER 200M测定动挠度的试验分析[J]. 大地测量与地球动力学, 2013(5): 116-119 (Liao Zhongping, Hua Sainan, Liu Ning, et al. Test Analysis on Determining Dynamic Deflection by R8 GNSS, TCA2003 and SPRINTER 200M[J]. Journal of Geodesy and Geodynamics, 2013(5): 116-119)
(  0) 0) |
| [5] |
耿会岩, 贾献卓, 李强. 桥梁结构挠度测试现状与展望[J]. 山西建筑, 2010, 36(29): 306-307 (Geng Huiyan, Jia Xianzhuo, Li Qiang. Status and Prospects Bridge Deflection Test[J]. Shanxi Architecture, 2010, 36(29): 306-307 DOI:10.3969/j.issn.1009-6825.2010.29.193)
(  0) 0) |
| [6] |
徐进军, 王海城, 罗喻真, 等. 基于三维激光扫描的滑坡变形监测与数据处理[J]. 岩土力学, 2010, 31(7): 2188-191 (Xu Jinjun, Wang Haicheng, Luo Yuzhen, et al. Deformation Monitoring and Data Processing of Landslide Based on 3D Laser Scanning[J]. Rock and Soil Mechanics, 2010, 31(7): 2188-191 DOI:10.3969/j.issn.1000-7598.2010.07.027)
(  0) 0) |
| [7] |
Fischler M A, Bolles R C. Random Sample Consensus a Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography[J]. Readings in Computer Vision, 1981, 24(6): 381-395
(  0) 0) |
| [8] |
潘国荣, 谷川, 王穗辉, 等. 三维激光扫描拟合直线自动提取算法研究[J]. 大地测量与地球动力学, 2009(1): 57-63 (Pan Guorong, Gu Chuan, Wang Suihui, et al. Research on Fitting Line Automatic Extraction Algorithm of 3D Laser Scanning[J]. Journal of Geodesy and Geodynamics, 2009(1): 57-63)
(  0) 0) |
| [9] |
马俊伟, 唐辉明, 胡新丽, 等. 三维激光扫描技术在滑坡物理模型试验中的应用[J]. 岩土力学, 2014, 35(5): 1495-1505 (Ma Junwei, Tang Huiming, Hu Xinli, et al. Application of 3D Laser Scanning Technology to Landslide Physical Model Test[J]. Rock and Soil Mechanics, 2014, 35(5): 1495-1505)
(  0) 0) |
2. Collaborative Innovation Center for Geospatial Technology, 129 Luoyu Road, Wuhan 430079, China
 2017, Vol. 37
2017, Vol. 37

