2. 桂林理工大学测绘地理信息学院, 桂林市雁山街319号, 541004;
3. 桂林理工大学广西矿冶与环境科学实验中心, 桂林市雁山街319号, 541004;
4. 空军大连通信士官学校, 大连市金州区, 116600;
5. 浙江省测绘大队, 杭州市三墩镇, 310030;
6. 城市空间信息工程北京市重点实验室, 北京市羊坊店路15号, 100038
在实际的观测环境中经常会存在动力模型不准确和观测模型出现粗差的情况,采用标准Kalman滤波无法抵御粗差对估值的影响,一般会通过引入1个自适应因子来进行调节[1-3]。本文在抗差Kalman滤波的基础上引入2个自适应因子分别对动态模型和观测模型进行调节,通过这2个自适应因子共同求出状态估值。然而在抗差自适应Kalman滤波中需对每一观测时刻的数据进行迭代计算,从而会使得运算时间变长,对数据的精度也会造成一定的影响。本文通过构建卡方统计量,提出基于卡方检验的抗差自适应Kalman滤波,并通过工程实例对其性能进行验证。
1 抗差自适应Kalman滤波当观测值存在粗差或者滤波发散等问题出现时,由于Kalman滤波不具备抗差性,易受到影响。针对此问题,杨元喜院士[4]提出了抗差自适应滤波,其基本思想是在测量值存在粗差时,对测量值使用抗差估计方案处理,在实现抗差估计的前提下,如果动力模型出现非正常误差,通过自适应因子对其调整。即在用Kalman滤波进行运算时,如果测量序列Lk中存在粗差,其滤波结果精度会降低。根据M估计等价权原理对增益矩阵进行分析可知,选择恰当的权函数替换观测噪声的协方差矩阵可以降低粗差对滤波估值精度的影响。利用自适应因子调节增益矩阵可以合理利用观测数据中的信息,减少测量粗差对平差后的结果带来的影响。抗差自适应Kalman滤波的改进部分如下[5-6]。
1)增益矩阵:
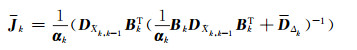
|
(1) |
2) 状态估计:
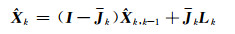
|
(2) |
3) 估计误差方阵:
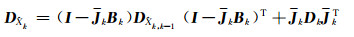
|
(3) |
4) 抗差自适应滤波的解:
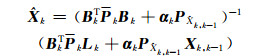
|
(4) |
式中,观测序列的协方差阵对应的权矩阵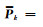
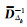 ,
,
当动态模型和观测模型均出现误差时,可以在抗差Kalman滤波中引入1个自适应因子对动态模型和观测模型进行调整,或在抗差自适应Kalman滤波基础上引入2个自适应因子对动态模型和观测模型进行调节,建立双自适应因子滤波算法。
2.1 滤波模型的推导动态向量的预报误差方程为:

|
(5) |
式中,动态向量预报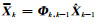
观测向量的误差方程为:
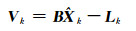
|
(6) |
式中,Vk反映的是观测值的误差。
通过最小二乘原理构造的损失函数为:
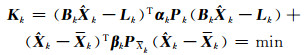
|
(7) |
式中,Pk和PXk分别为Lk的等价权矩阵和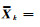
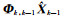

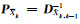
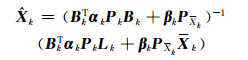
|
(8) |
通过矩阵的恒等变换可知:

|
(9) |
式中,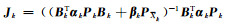
自适应因子构造方法是根据指数型的两段法的计算方法,得到观测模型的自适应因子αk和动力学模型自适应因子βk:
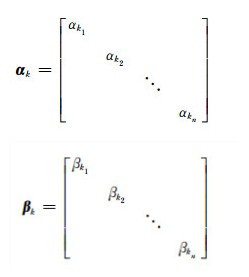
|
式中,αki∈[0, 1],βki∈[0, 1]。
1) 自适应因子αk的选取
公式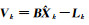


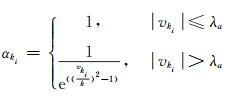
|
(10) |
式中,λa是一个阈值,取值范围为λa∈[1.0, 3.0]。
2) 自适应因子βk的选取
模型信息的准确性是通过式(5)反映的,将式(9)代入式(5)得:
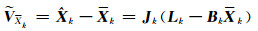
|
(11) |
式(9)作为动态的预测残差,通过对其第i项分量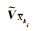

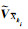
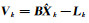

|
(12) |
式中,λβ是一个阈值,取值范围为λβ∈[1.0, 3.0][7]。
3 基于卡方检验的抗差自适应Kalman滤波在本节中,离散系统的动态方程和观测方程与离散系统下的标准Kalman滤波的相同。判断粗差是否存在,主要根据Kalman滤波中的预测残差。预测残差为观测值的预测值与实际观测值之差,即

|
(13) |
式中,状态预测值和观测预测值分别为:
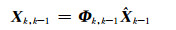
|
(14) |
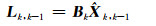
|
(15) |
如果测量值Lk正常,且预测值也准确,则预报值与观测值的观测误差服从正态分布。同样,残差Vk也服从正态分布,其协方差矩阵是:
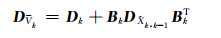
|
(16) |
式中,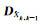
在粗差混入观测数据的情况下,残差的分布会偏离正态分布。由于各观测值相互独立,则统计量为:
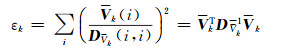
|
(17) |
式中,Vk(i)表示第i个观测残差,DVk(i,i)为Vk的协方差矩阵上对角线上的元素[10]。在Lk中无粗差的情况下,统计量εk服从自由度为1的中心χ2分布,反之εk服从自由度为1的非中心χ2分布。
检验方法如下。原假设H0:观测值中无粗差;备选假设H1:观测值中存在粗差。显著性水平为a,若εk≤χa2(1),则接受H0假设,检验通过;反之,拒绝H0假设,接受H1假设。χa2(1)为χ2(1)分布上的a分位数。
在观测值中可能存在粗差的情况下,首先采用上述方法进行检验。如果存在粗差,则进行抗差迭代,得到精确状态估值;如果不存在粗差,无需进行抗差迭代,以Kalman滤波得到的估值作为滤波结果。
4 实例分析在实际观测中异常值不仅仅是含有粗差,还有可能是环境因素使得形变异常,故在进行粗差探测前需对异常值进行处理。我们选取贵广高铁某隧道观测了16期的水准网进行分析,该数据中无异常形变值,其水准网采用二等精密水准测量,在平差后该数据的精度符合相应精度要求。为了检验自适应双因子滤波法的抗差效果,对该水准网中变形监测点某点的第8期加入2 mm(远大于2倍中误差)的粗差,观测周期为7 d。通过使用双自适应因子滤波算法、基于卡方分布的抗差自适应Kalman滤波对加入粗差后的观测数据进行滤波,然后与标准Kalman滤波的滤波估计进行对比,对比结果如图 1~3。
|
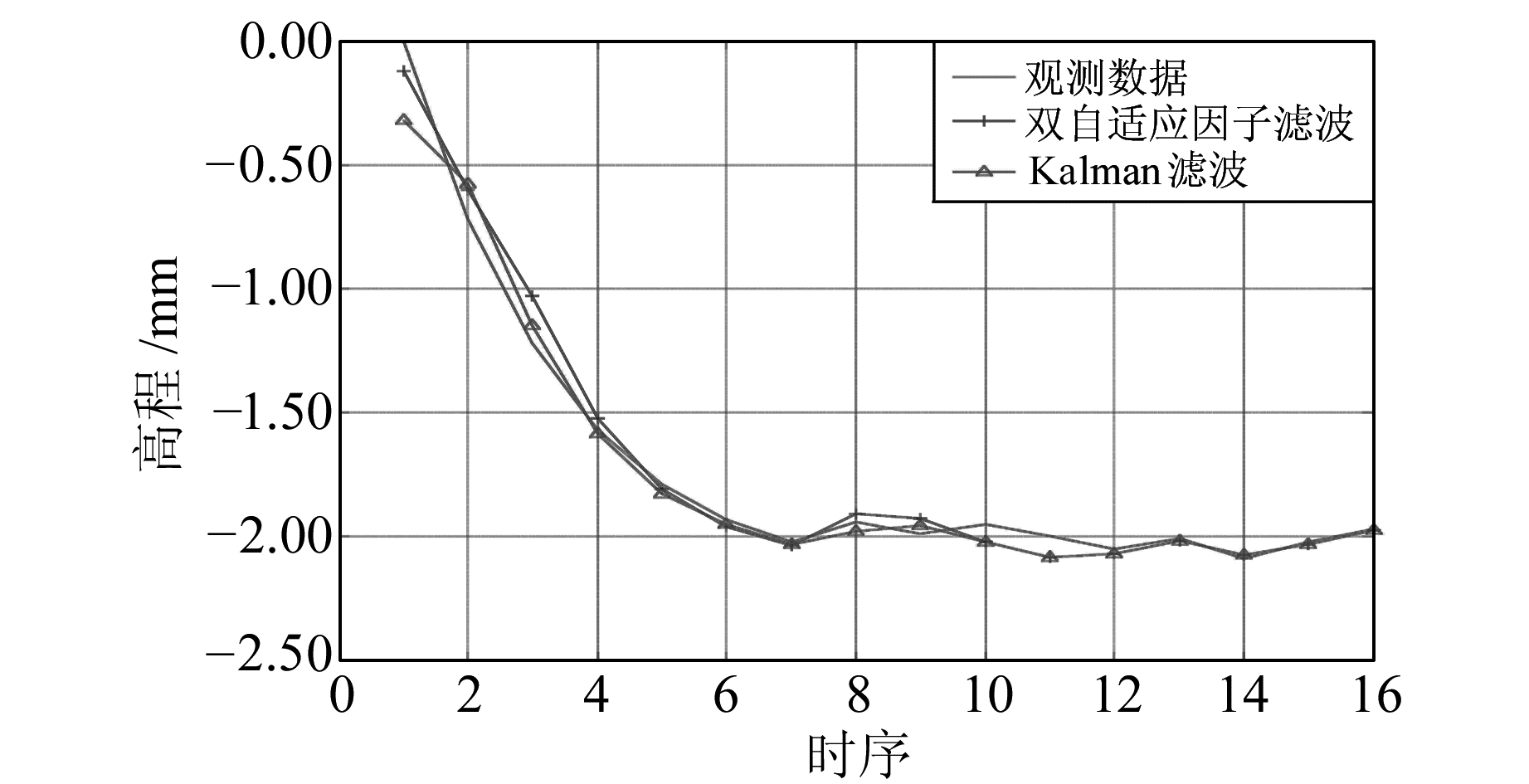
图 1 无粗差时双自适应因子滤波与标准Kalman滤波的结果对比 Fig. 1 Comparison between the results of dual adaptive factor filter without gross error and standard Kalman filter |

|
图 2 双自适应因子滤波结果与含粗差观测数据的对比 Fig. 2 Comparison between the results of dual adaptive factor filter and measured values with gross error |
|
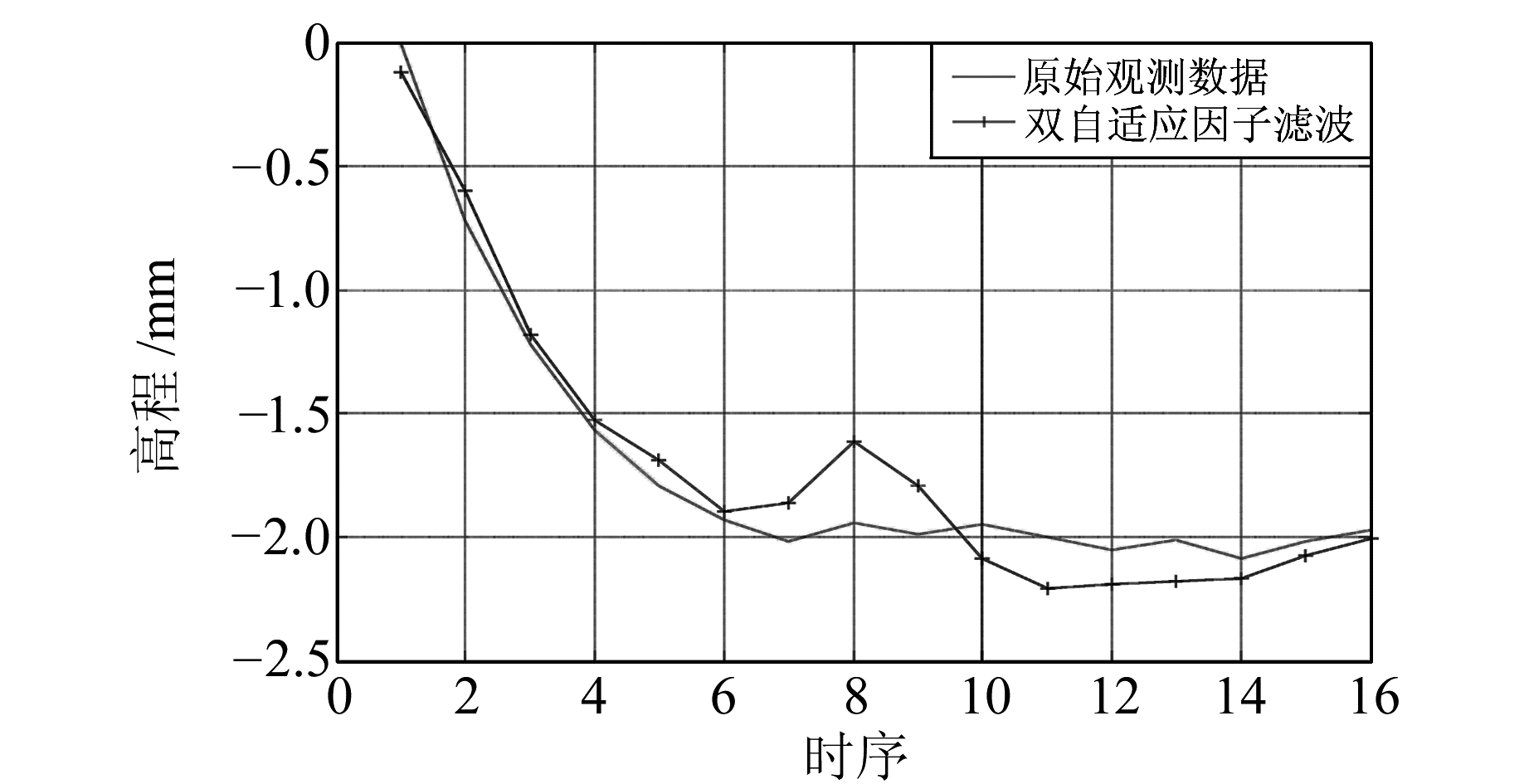
图 3 双自适应因子滤波算法结果与原始观测值的对比 Fig. 3 Comparison between the results of dual adaptive factor filter and measured values |
在观测数据中不含粗差时,双自适应因子滤波和标准Kalman滤波的处理结果如图 1。由图 1可知,在观测数据中无粗差时,双自适应因子滤波与标准Kalman滤波的结果十分接近,即使在初始值存在一定误差的情况下也可以快速收敛。因此,这两种方法在不含粗差的情况下是等效的。在观测数据中加入粗差后采用双自适应因子滤波和标准Kalman滤波的处理结果见图 2、图 3。由图可知,当观测数据中存在粗差时,双自适应因子滤波结果与无粗差的观测数据的观测值十分接近,说明双自适应因子能够有效地抑制粗差对滤波估值的影响。
用3种方法(方法1:双自适应因子滤波;方法2:抗差自适应Kalman滤波;方法3:基于卡方分布的抗差自适应Kalman滤波)进行数据处理,其滤波估值的方差见表 1(单位mm2),各模型的处理结果见图 4~7。
|
|
表 1 3种方法滤波估值的方差 Tab. 1 The variances of three models |
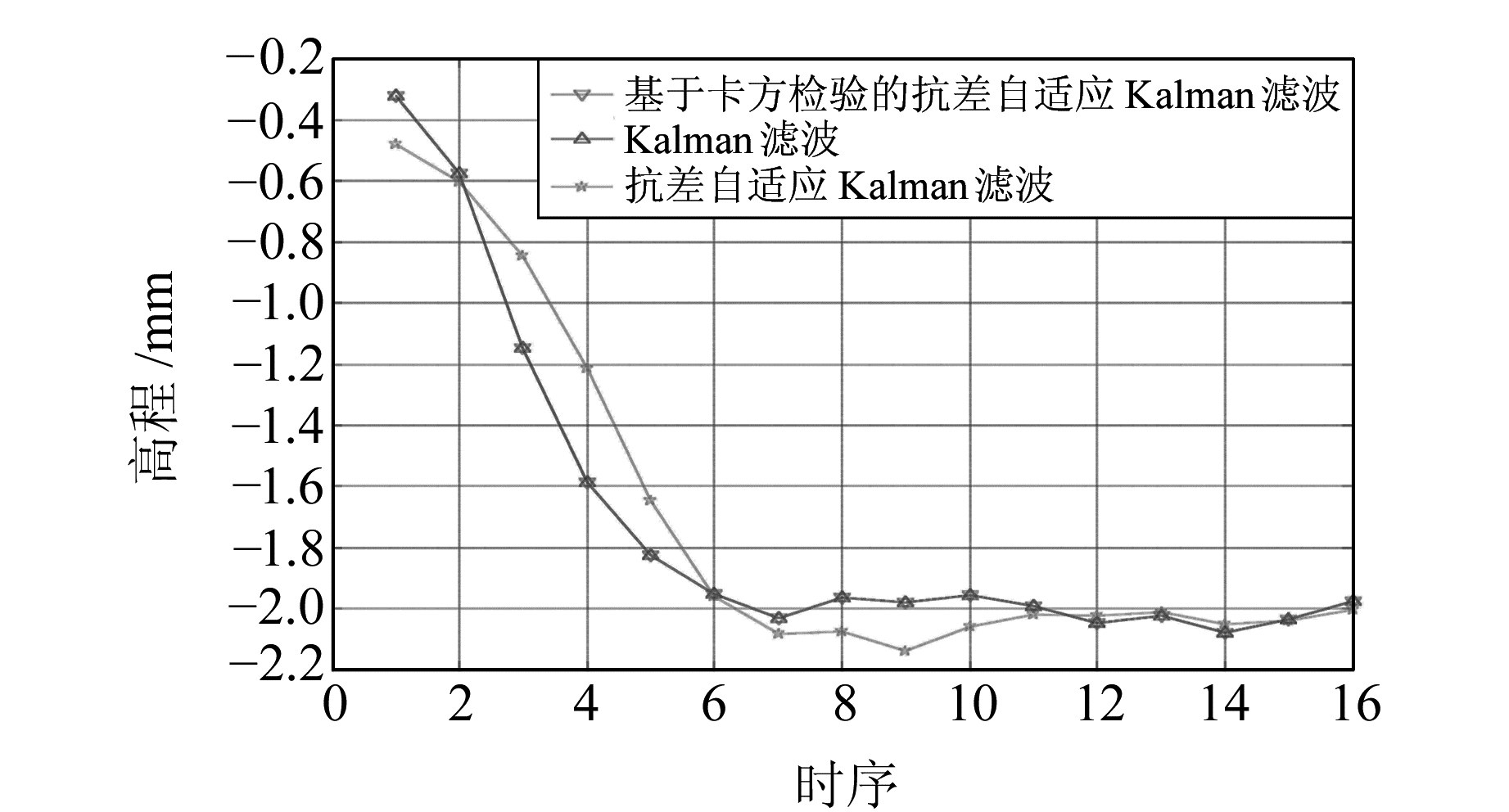
|
图 4 无粗差时各模型结果的对比 Fig. 4 Comparison between the results of two models without gross error |
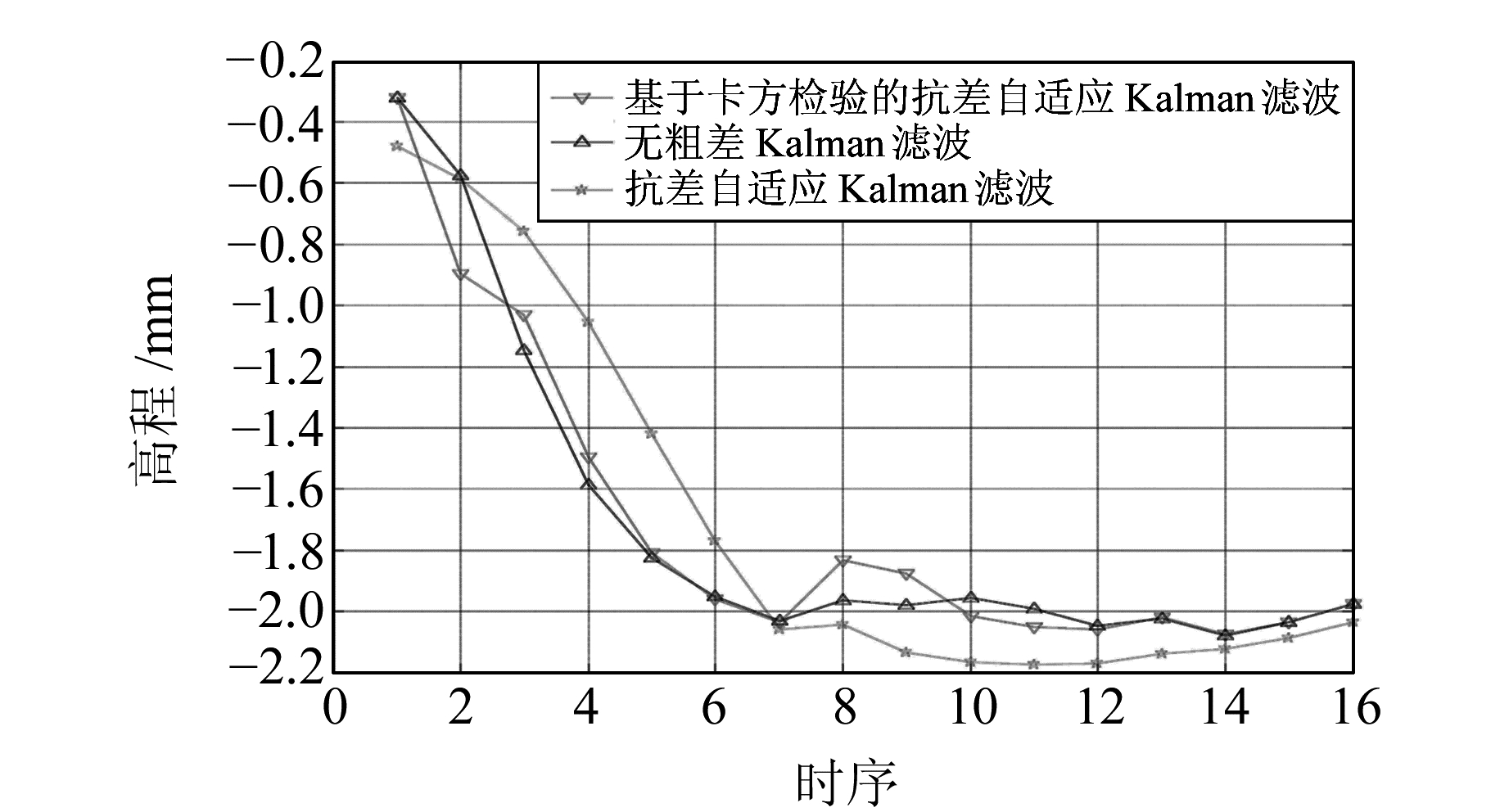
|
图 5 含有粗差时各模型结果的对比 Fig. 5 Comparison between the results of two models with gross error |
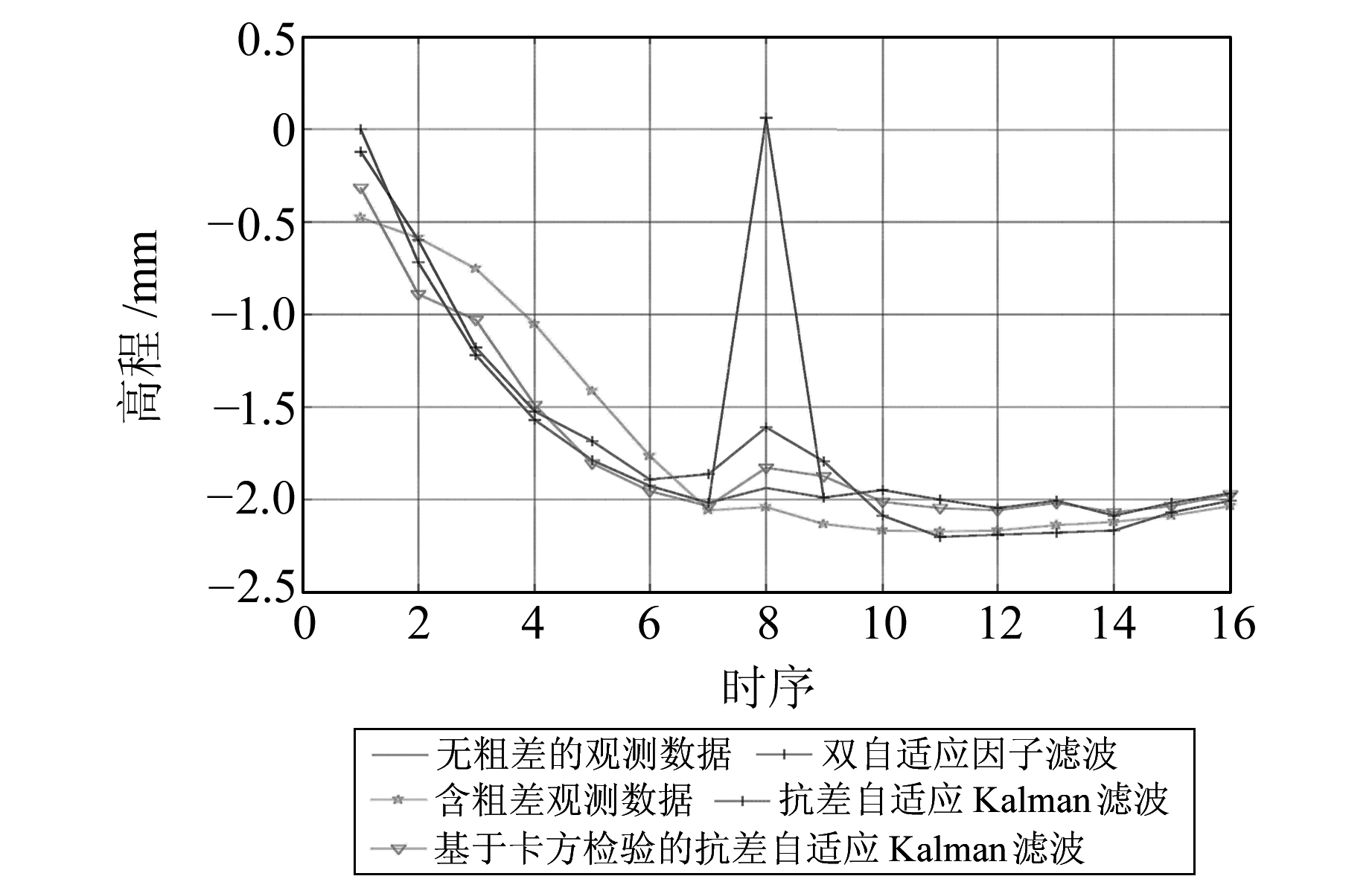
|
图 6 多模型处理结果与原始观测数据对比 Fig. 6 Comparison between the results of three models and measured values |
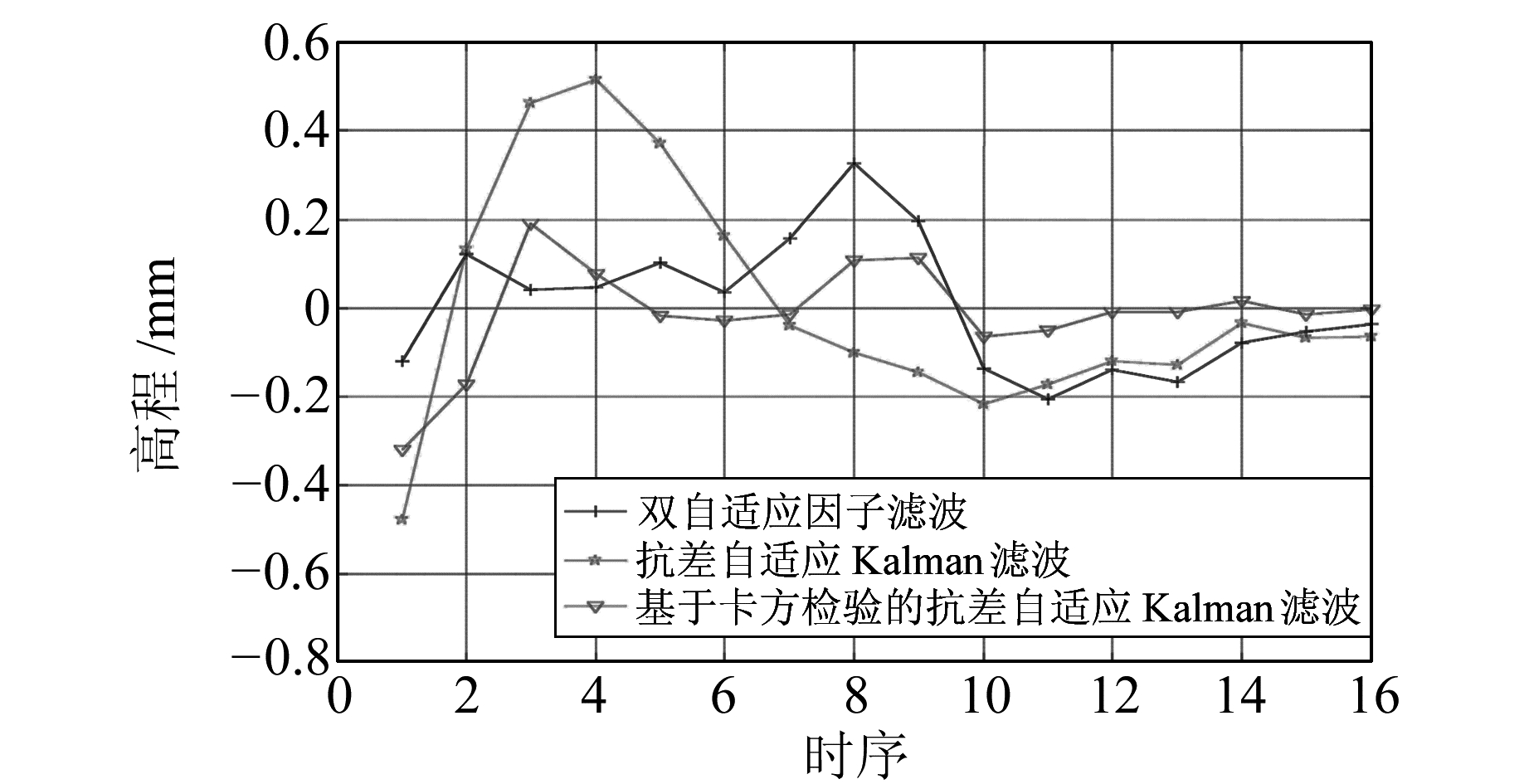
|
图 7 多模型处理结果残差 Fig. 7 The residual of three models |
由图 4可知,当观测数据中无粗差时,抗差自适应Kalman滤波估值与标准Kalman滤波估值均随着时间的增加而收敛,但是抗差自适应Kalman滤波的收敛速度明显比标准Kalman滤波慢。这是因为抗差自适应Kalman滤波对每一时刻的观测值均进行了抗差迭代,从而会使得计算时间变长,估计精度也随之降低。
由图 5可知,在观测值中含有粗差时,基于卡方检验的抗差自适应Kalman滤波的估值与无粗差的观测数据十分接近,而且可以快速收敛,其精度也优于抗差自适应Kalman滤波。这是由于该算法综合了统计模型,通过统计检验先对粗差进行判别,使得计算效率和精度均得到了提高。
通过图 6、图 7以及表 1可知,对于小范围内的粗差,双自适应因子滤波模型的滤波精度要优于抗差自适应Kalman滤波。在小范围存在粗差和短时间内,双自适应因子滤波不仅可以抵御粗差对滤波估值的影响,同时可以削弱动态模型不准确的影响。通过均方误差可以看出,双自适应因子滤波与抗差自适应Kalman滤波的抗差性能均比较稳定。通过图 7的残差图和均方误差可知,基于卡方检验的抗差自适应Kalman滤波的效率和稳定性均优于抗差自适应Kalman滤波和双自适应因子滤波。
5 结语本文将双自适应因子滤波算法、基于卡方检验的抗差自适应Kalman滤波应用于隧道的沉降变形观测。工程实例证明,双自适应因子滤波在小范围内存在粗差的情况下优于抗差自适应Kalman滤波,该算法可以很好地抵制粗差,减弱粗差对滤波估值的影响。而基于卡方检验的抗差自适应Kalman滤波的性能和效率均优于双自适应因子滤波和抗差自适应Kalman滤波。由于这两个自适应因子存在一定的相关性,如何消除该影响仍需进一步研究。
| [1] |
崔先强, 杨元喜. 分类因子自适应抗差滤波[J]. 自然科学进展, 2006, 16(4): 490-494 (Cui Xianqiang, Yang Yuangxi. Classified Factors Robust Adaptive Filter[J]. Progress in Natural Materials, 2006, 16(4): 490-494 DOI:10.3321/j.issn:1002-008X.2006.04.017)
(  0) 0) |
| [2] |
文鸿雁, 周吕, 韩亚坤. 基于卡尔曼滤波的GM(1, 1)模型在高铁隧道沉降变形分析中的应用[J]. 大地测量学与地球动力学, 2014, 34(1): 88-91 (Wen Hongyan, Zhou Lü, Han Yakun. Application of GM (1, 1) Model Based on Kalman Filter to the Subsiding Analysis of High Speed Railway Tunnel[J]. Journal of Geodesy and Geodynamics, 2014, 34(1): 88-91)
(  0) 0) |
| [3] |
赵长胜. 有色噪声滤波理论与算法[M]. 北京: 测绘出版社, 2011 (Zhao Changsheng. Colored Noise Filtering Theory and Algorithms[M]. Beijing: Surveying and Mapping Press, 2011)
(  0) 0) |
| [4] |
杨元喜. 自适应动态导航定位[M]. 北京: 测绘出版社, 2006 (Yang Yuanxi. Adaptive Navigation and Kinematic Positing[M]. Beijing: Surveying and Mapping Press, 2006)
(  0) 0) |
| [5] |
余学祥, 吕伟才. 抗差卡尔曼滤波模型及其在GPS监测网中的应用[J]. 测绘学报, 2001, 30(1): 27-31 (Yu Xuexiang, Lü Weicai. Robust Kalman Filter Model and Its Application in GPS Monitoring Networks[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(1): 27-31 DOI:10.3321/j.issn:1001-1595.2001.01.006)
(  0) 0) |
| [6] |
伍锡锈, 戴吾蛟, 罗飞雪. 抗差自适应Kalman滤波在动态变形监测中的应用研究[J]. 防灾减灾工程学报, 2011, 31(1): 102-106 (Wu Xixiu, Dai Wujiao, Luo Feixue. Research on Adaptively Robust Kalman Filtering for Dynamic Deformation Monitoring Applications[J]. Journal of Disaster Prevention and Mitigation Engineering, 2011, 31(1): 102-106)
(  0) 0) |
| [7] |
苏天祥, 文援兰, 朱俊. 双自适应因子滤波算法[J]. 测绘学报, 2015, 44(1): 26-31 (Su Tianxiang, Wen Yuanlan, Zhu Jun. The Algorithm of Dual Adaptive Factors Filtering[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(1): 26-31)
(  0) 0) |
| [8] |
刘茂华, 尹潇, 吕志鹏, 等. 基于移动窗口的抗差自适应滤波算法研究[J]. 大地测量学与地球动力学, 2014, 34(6): 140-143 (Liu Maohua, Yin Xiao, Lü Zhipeng, et al. Research of Robust Adaptive Filtering Based on Moving Window[J]. Journal of Geodesy and Geodynamics, 2014, 34(6): 140-143)
(  0) 0) |
| [9] |
苗岳旺, 周巍, 田亮, 等. 基于信息χ2监测的扩展抗差卡尔曼滤波及其应用[J]. 武汉大学学报:自然科学版, 2016, 41(2): 269-273 (Miao Yuewang, Zhou Wei, Tian Liang, et al. Extend Robust Kalman Filter Based on Innovation Chi-Square Test Algorithm and Its Application[J]. Geomatics and Information Science of Wuhan University, 2016, 41(2): 269-273)
(  0) 0) |
| [10] |
张艺航, 陈树新, 吴昊, 等. 基于抗差EKF的机载单站无源定位算法[J]. 空军工程大学学报:自然科学版, 2014, 15(4): 75-78 (Zhang Yihang, Chen Shuxin, Wu Hao, et al. Airborne Single-Observer Passive Location Algorithm Based on Robust EKF[J]. Journal of Air Force Engineering University(Natural Science Edition), 2014, 15(4): 75-78)
(  0) 0) |
2. College of Geomatics and Geoinformation, Guilin University of Technology, 319 Yanshan Street, Guilin 541004, China;
3. Guangxi Scientific Experiment Center of Mining, Metallurgy and Environment, Guilin University of Technology, 319 Yanshan Street, Guilin 541004, China;
4. Dalian Airforce Communication NCO Academy, Jinzhou District, Dalian 116600, China;
5. Zhejiang Brigade of Surveying and Mapping, Shandun Town, Hangzhou 310030, China;
6. Beijing Key Laboratory of Urban Spatial Information Engineering, 15 Yangfangdian Road, Beijing 100038, China
 2017, Vol. 37
2017, Vol. 37



