2. 江苏万源测绘地理信息有限公司, 连云港市通灌南路95号,222000
随着各种超大型地下工程的迅速涌现,深基坑工程愈来愈多,且随着开挖深度与面积日益增加,其稳定性与安全性日益引起全社会的关注,准确预测基坑变形成为一项非常重要的工作。在基坑围护结构、复杂地质条件及外力等因素影响下,很难找到一种确定的预测模型预测其变化趋势。为揭示基坑监测数据的内在结构与变化规律,预测基坑未来变化趋势,近年来国内外学者提出多种预测模型,并应用到基坑变形预测中,如灰色模型[1]、时间序列模型[2]、神经网络模型[3-4]等单一模型以及小波-支持向量机[5]等组合模型。基坑变形具有较大的随机性、不确定性与复杂性,单一预测模型很难充分挖掘原始时间序列中的信息且未考虑随机项与趋势项的影响,同时预测精度也有待提高。Huang等[6]在经验模态分解(empirical mode decomposition,EMD)基础上提出一种以噪声辅助的分解方法——集成经验模态分解(ensemble empirical mode decomposition,EEMD),不仅具有小波多分辨率优点,也具有良好的局部化、自适应和分析结果直观性等优点。支持向量机[7](support vector machine,SVM)是在统计学习VC维理论和结构化风险最小的原则上建立的,能够很好地解决小样本、非线性及高维模式识别等实际问题。粒子群优化算法[8](particle swarm optimization, PSO)是通过迭代寻找最优解,该算法易实现、精度高、收敛快且适用于高维数据处理,被广泛应用于SVM参数寻优。
针对基坑位移预测的难点与单一模型的不足,提出将EEMD分解、相空间重构与灰色支持向量机(GSVM)相结合的方法进行基坑变形预测。首先对时间序列进行混沌序列识别,使用EEMD分解时间序列,得到具有不同特征尺度的本征模态函数(intrinsic mode function,IMF)与趋势项,然后采用相空间重构技术构造样本,最后采用灰色支持向量机(grey support vector machine,GSVM)对重构分量分别建立预报模型,将各分量预测值叠加,再将叠加值累减得最终预测值,同时采用PSO优化灰色支持向量机参数。与不同预报进行对比分析,验证该方法的可行性与有效性。
1 EEMD滤波分解原理在原始信号上加上均匀分布、有限幅值的白噪声,信号内不同尺度的成分自动映射到背景白噪声建立的相关的适当尺度上,采用EEMD方法将信号分解成具有不同特征尺度的IMF分量之后,对每一个IMF进行Fourier变换,解决EMD分解的边界效应。根据EEMD分解特性及尺度逐步递增等特点,通过分析分解后的各个IMF分量频谱特征,可有效地对信号进行降噪处理, 其分解流程见参考文献[9]。
2 相空间重构理论 2.1 相空间重构原理相空间重构[10]是研究混沌时间序列的基础,其目的是从时间序列中重构一组在拓扑意义上与原动力系统等价的相空间,在重构的相空间中可完成对混沌时间序列的判定、分析与预测。相空间重构常采用坐标延迟重构,其本质是通过序列点之间不同的延迟时间来重新构造m维相空间,其构造如下:
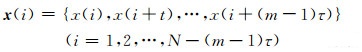
|
(1) |
式中,m为嵌入维数,τ为延迟时间N为时间序列个数,x(i)为序列中的点;当m≥2d+1时,d表示相空间维数。
相空间重构的关键在于m与τ的选取,实际基坑观测时间序列的周期有限,延迟时间通常取1[11]。目前,时间选取方法主要有自相关函数法、复相关法、互信息法等。自相关函数法与互信息法都是选取函数在第一次达到最小时的值,自相关函数法只能判断线性相关性;互信息法还能够提取空间的非线性相关性,其计算结果比自相关函数法好[12],故本文选取互信息法确定重构相空间的延迟时间。
相空间嵌入维数的确定方法主要有几何不变量法、G-P法、虚假最邻近法(false neatest neighbors,FNN)、Cao法、C-C法等[10],本文选取在FNN基础上加以改进的Cao法确定最小嵌入维数。
2.2 混沌特性识别混沌系统以Lyapunov指数来衡量系统对初始条件的敏感性,Lyapunov指数表示系统在重构相空间中相邻轨迹之间的发散平均指数率。某时间序列的最大Lyapunov指数比大于0,说明该时间序列具有混沌特性。深基坑位移监测序列周期一般不长,本文采用小数据量法[13]计算基坑位移序列的最大Lyapunov指数,以判定其混沌性。
3 PSOGSVM 3.1 GSVM理论设原始变形时间序列为{ x10, x22, …, xn0},其中n表示监测期数。首先对原始时间序列进行一次累加:

|
(2) |
将得到规律性更强的序列。以新序列的前m期作为训练数据,n-m期作为测试数据,用GSVM建立预测模型[14],最后对累加序列的预测值y={y1, y2, …, yn}进行累减,得到原始序列的预测值:

|
(3) |
GSVM预测效果在很大程度上取决于核函数k(x, y)、核参数σ、正则化参数C的选取,目前SVM参数优化方法主要有网格搜索法、遗传算法、PSO等。PSO是模拟鸟群捕食行为,通过迭代搜寻全局最优值的方法,能够克服传统优化方法的缺点,较为快速地得到最优化组合,故本文采用粒子群优化算法搜寻支持向量机的最优参数组合[15]。
4 EEMD与PSOGSVM耦合预报模型EEMD与PSOGSVM耦合预报模型具体预测流程见图 1。首先对原始时间序列{X(t), t=1, 2, …, m}进行混沌序列识别,然后通过EEMD滤波进行分解得到n个高频IMF以及一个低频余量A:
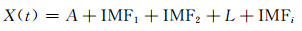
|
(4) |

|
图 1 模型预测流程 Fig. 1 Flow chart of model prediction |
对各个分量IMF采用相空间重构技术得到新的子序列imf={imf1, imf2, …, imfj,=1, 2, …, i},以确定的嵌入维数m与延迟时间τ建立训练样本。用前t期作为训练数据,后n-t期作为测试样本,建立GSVM预测模型,得到对应序列的预测值向量为F ={F1, F2, …,Fj},预测值结果为:
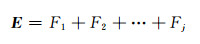
|
(5) |
将最终预测值进行累减处理,得到时间序列的预测值。
5 实例解算以华为四万车库基坑桩顶S17号观测点的位移监测数据资料为例。时间序列长度为50期,以前45期数据作为训练样本,后5期作为测试数据,原始数据序列如图 2所示。

|
图 2 基坑位移观测值变化曲线 Fig. 2 Durationcurve of measured foundation pit displacement |
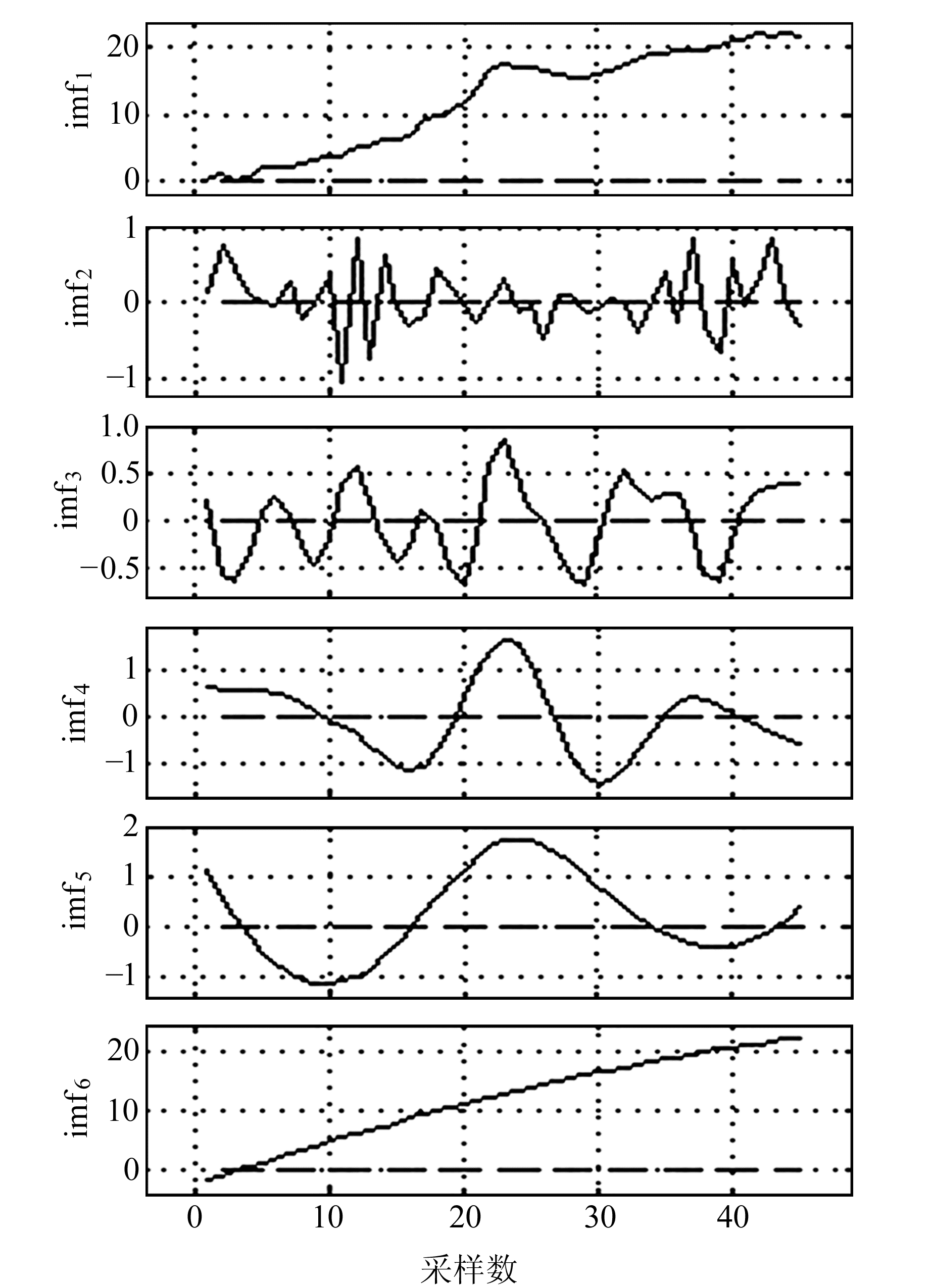
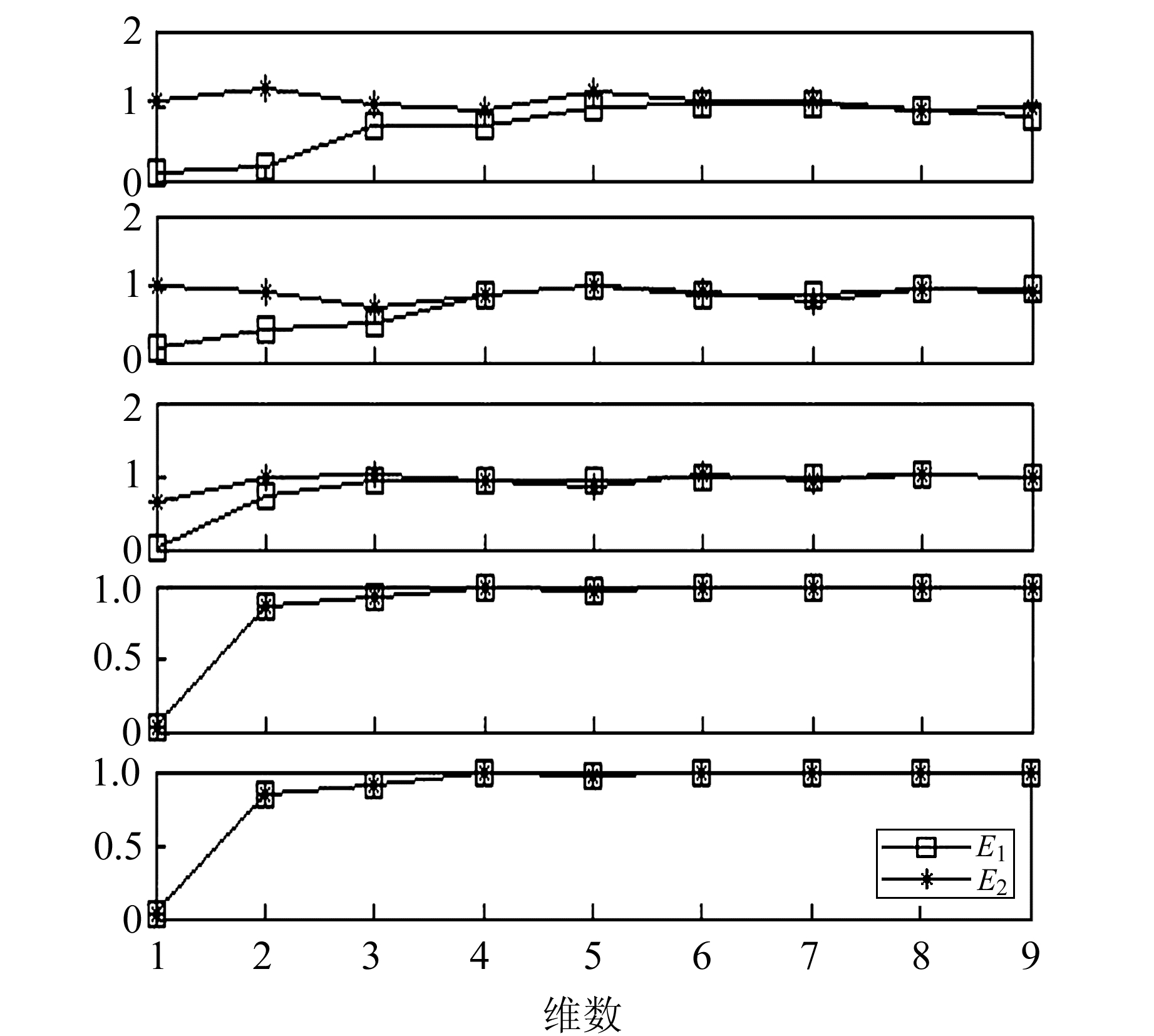
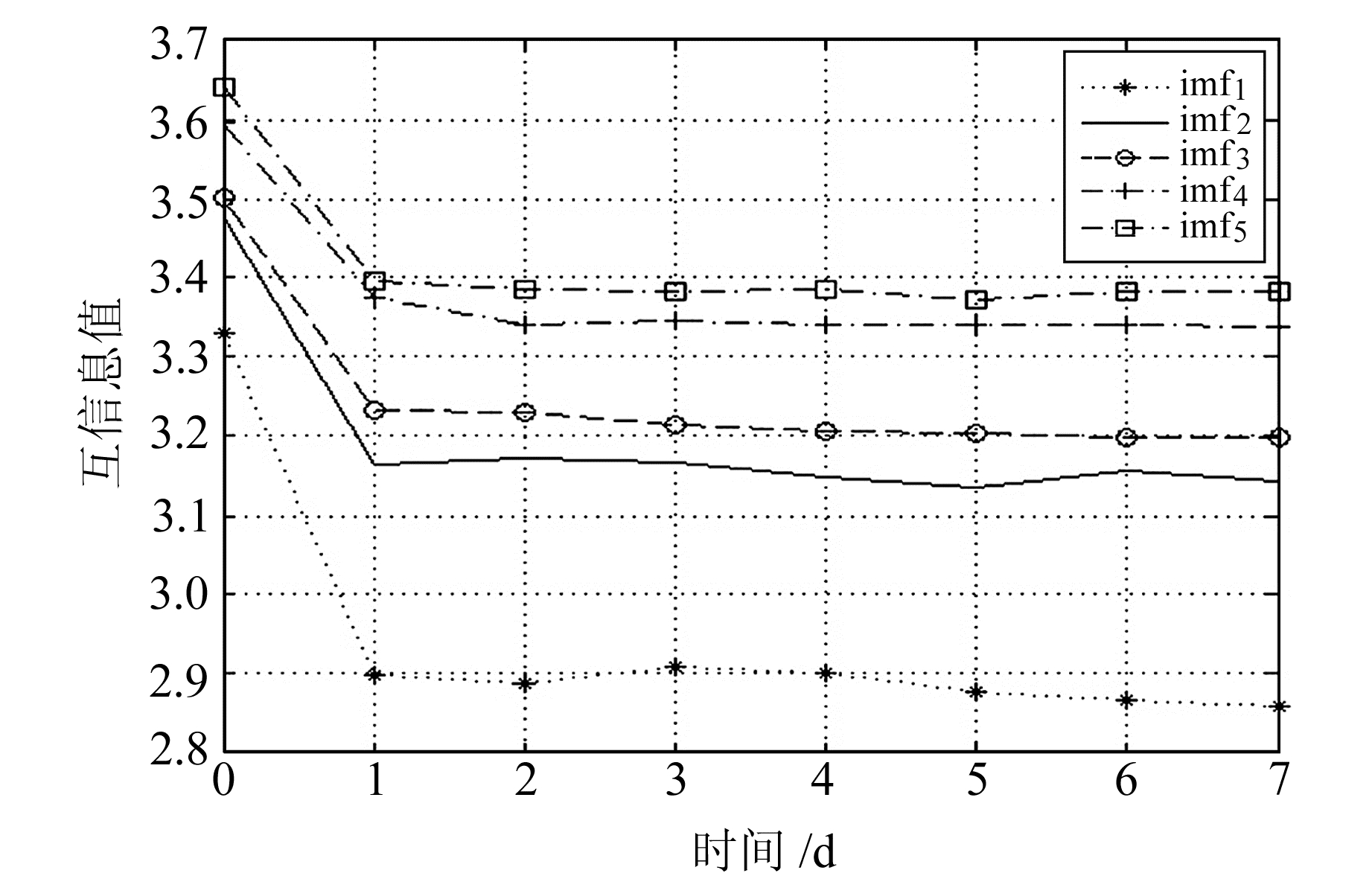
通过计算, 原始时间序列的维数为6,延迟时间为2,lyapunov最大指数为0.006 2,说明该时间序列具有混沌特性。为分析时间序列中的隐含信息,采用EEMD分解时间序列,得到1个原始数据序列、4个IMF分量以及一个趋势项A,结果如图 3所示。可以看出,分量imf2~imf5序列趋于平稳,且频率在逐渐降低;imf2和imf3变化比较剧烈,说明之间关联性不大,具有一定的随机性。EEMD分解能得到不同尺度下的序列信号。为消除各个不同维数之间数量级差别以及模型预测的误差,将各子序列进行归一化处理,归一化到区间[-1, 1]。利用相空间重构Cao法与互信息法求各分量时间序列的嵌入维数以及延迟时间,与图 3中的分量相对应,图 4与图 5分别表示相应的嵌入维数与延迟时间变化趋势,其嵌入维数分别为6、4、4、5、8,延迟时间分别为1、2、1、1、1。
|
图 3 分解后的各分量序列 Fig. 3 Decomposedcomponents series |
|
图 4 Cao方法确定嵌入维数 Fig. 4 Computing embedding dimension using Cao's method |
|
图 5 互信息法选择延迟时间 Fig. 5 Defermining delay time by AMI |
以时间序列的前45期数据作为训练样本,预测下一周期位移值,并结合46~49期实测数据继续预测下一周期位移值,直至预测5个周期的位移值为止,以证明模型预测效果。在各分量嵌入维数与延迟时间下重构训练样本与测试样本,用PSOGSVM预测模型对各个分量进行训练与测试,核函数为RBF核,得到各分量所对应的最优模型参数如表 1所示,表中C为惩戒因子,σ为核宽度。
|
|
表 1 各分量PSOGSVM预测模型参数 Tab. 1 PSOGSVM forecasting model parameters for decomposed components |
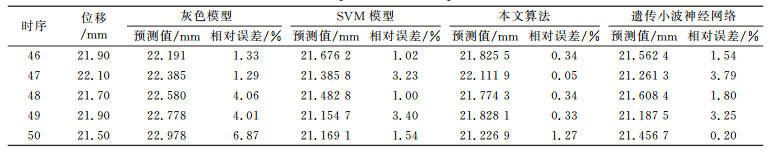
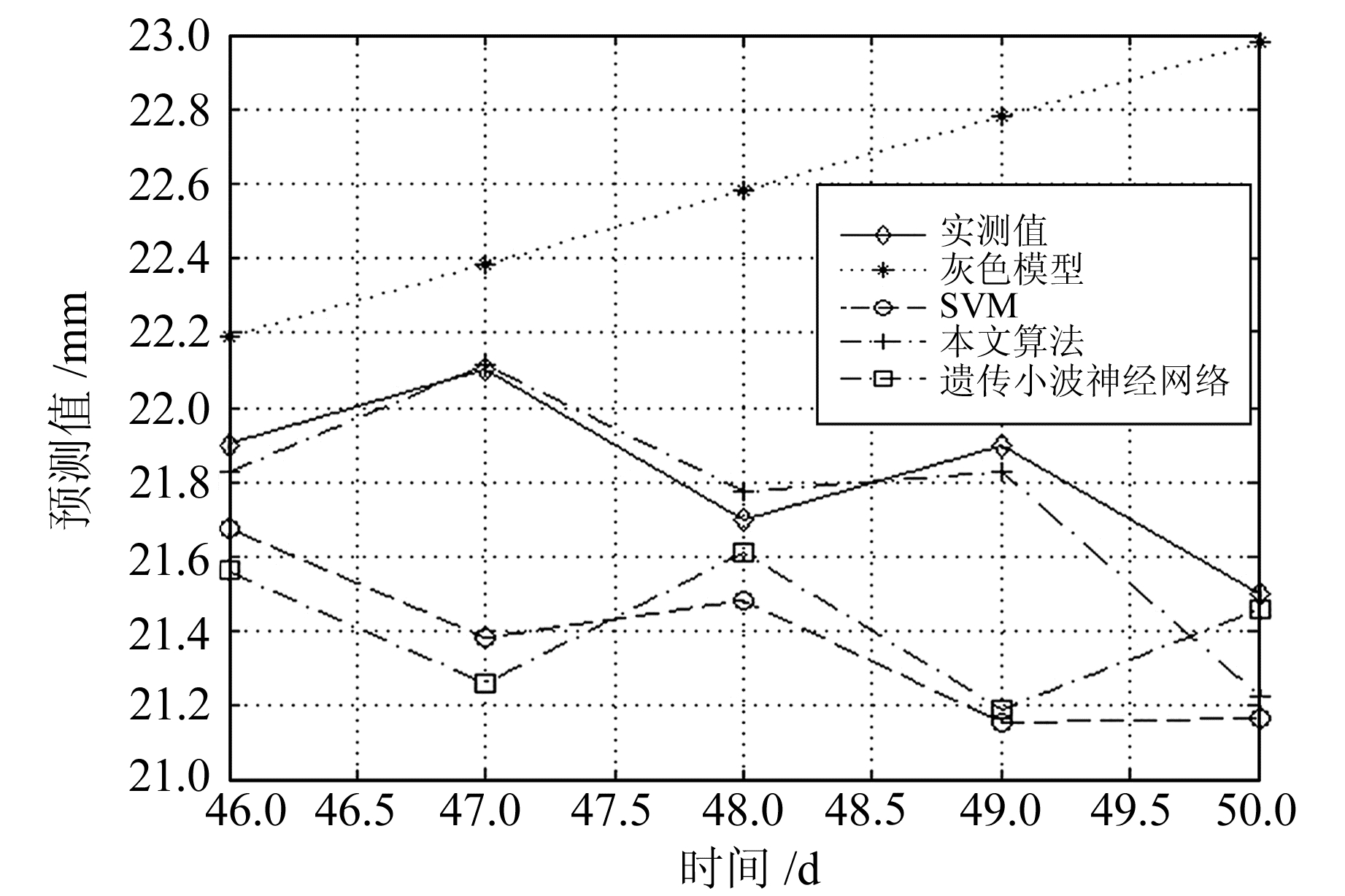
利用预测模型对各个分量进行预测,将得到的分量预测值叠加得到基坑位移序列的预测值。为验证预测模型的可行性、精确性与可行性,与3种单一预测模型结果进行对比分析。分别采用灰色模型、SVM、遗传小波神经网络进行预测,后两种模型的嵌入维数为6,延迟时间为1,其中SVM的参数为C=1 024,σ=0.000 976,3种模型的计算结果如图 6所示,计算结果及相对误差见表 2。由表 2及图 6知,PSOGSVM模型预测值变化趋势与实测值基本一致,且相对误差最小为0.05%,最大为1.27%,平均为0.466%,SVM的平均相对误差仅达到2.308%,遗传算法优化的小波神经网络的平均误差为2.116%。本文算法更能有效地应用于深基坑位移预测。
|
|
表 2 模型预测值对比 Tab. 2 Comparison of model predictions |
|
图 6 模型预测值比较 Fig. 6 Comparison of several results obtained by different models |
1) 基于基坑位移时间序列混沌特性,提出EEMD与PSOGSVM耦合预测模型。该模型应用混沌理论判定时间序列的混沌性,利用EEMD将基坑位移序列分解为具有不同特征尺度的分量,应用Cao法与互信息法确定各分量嵌入维数与延迟时间、重构序列,采用PSOGSVM模型进行预测。结果表明,该方法能够有效地提高基坑位移预测精度。
2) 在预报精度方面,耦合预测模型明显好于灰色模型、SVM模型以及遗传算法优化的小波神经网络等,具有较强的预报能力与预报精度,能够更好地应用于基坑位移预报。
3) 算法有机地结合多种模型特性,在某种程度上增加了模型复杂度,如何进一步优化模型运行效率与性能,建立更为精准的预报模型,需进一步深入研究。
| [1] |
王强, 刘松玉, 童立元, 等. 灰色理论在深基坑支挡结构变形预测中应用[J]. 岩土工程学报, 2010, 32(增刊2): 69-72 (Wang Qiang, Liu Songyu, Dong Liyuan, et al. Predicting Deformation of Retaining Structures in Foundation Pit by Grey System Theory[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(S2): 69-72)
(  0) 0) |
| [2] |
徐峰, 汪洋, 杜娟, 等. 基于时间序列分析的滑坡位移预测模型研究[J]. 岩石力学与工程学报, 2011, 30(4): 746-751 (Xu Feng, Wang Yang, Du Juan, et al. Study of Displacement Prediction Model on Time Series Analysis[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(4): 746-751)
(  0) 0) |
| [3] |
李龙, 高永涛, 吴顺川, 等. 综合改进BP神经网络在边坡稳定性预测中的应用[J]. 煤炭技术, 2015, 34(9): 202-205 (Li Long, Gao Yongtao, Wu Shunchuan, et al. Application of Comprehensive Improvement of BP Neural Network in Stability Prediction of Slop[J]. Coal Technology, 2015, 34(9): 202-205)
(  0) 0) |
| [4] |
潘国荣, 谷川. GMDH神经网络算法在变形预测中的应用[J]. 大地测量与地球动力学, 2008, 28(3): 54-58 (Pan Guorong, Gu Chuan. GMDH NN Algorithm and Its Application in Deformation Forecasting[J]. Journal of Geodesy and Geodynamics, 2008, 28(3): 54-58)
(  0) 0) |
| [5] |
范千, 花向红. 基于相空间重构与支持向量机预测滑坡位移的一种新方法[J]. 武汉大学学报:信息科学版, 2009, 34(2): 248-251 (Fan Qian, Hua Xianghong. A Novel Method for Forecasting Landslide Displacement Based on Phase Space Reconstruction and Support Vector Machine[J]. Geomatics and Information Science of Wuhan University, 2009, 34(2): 248-251)
(  0) 0) |
| [6] |
Huang N E, Shen Z, Long S R, et al. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis[J]. Proceedings of the Royal Society London A, 1998, 454: 903-995 DOI:10.1098/rspa.1998.0193
(  0) 0) |
| [7] |
Cortes C, Vapnik V. Support Vector Networks[J]. Machine Learning, 1995, 20(3): 273-297
(  0) 0) |
| [8] |
高卫峰, 刘三阳. 一种高效粒子群优化算法[J]. 控制与决策, 2011, 26(8): 1158-1162 (Gao Weifeng, Liu Sanyang. An Efficient Particle Swarm Optimization[J]. Control and Decision, 2011, 26(8): 1158-1162)
(  0) 0) |
| [9] |
徐佳, 麻凤海, 杨帆. EEMD滤波技术在GPS动态监测数据去噪中的应用[J]. 测绘科学, 2012, 37(3): 159-160 (Xu Jia, Ma Fenghai, Yang Fan. Research on Denosing GPS Dynamic Monitoring Data Based on EEMD Filter[J]. Science of Surveying and Mapping, 2012, 37(3): 159-160)
(  0) 0) |
| [10] |
张淑清, 贾健, 高敏, 等. 混沌时间序列重构相空间参数选取研究[J]. 物理学报, 2010, 59(3): 1576-1582 (Zhang Shuqing, Jia Jian, Gao Min, et al. Study on the Parameters Determination for Reconstructing Phase-Space in Chaos Time Series[J]. Acta Physica Sinica, 2010, 59(3): 1576-1582)
(  0) 0) |
| [11] |
马文涛. 基于小波变换和GALSSVM的边坡位移预测[J]. 岩土力学, 2009, 30(增刊2): 394-398 (Ma Wentao. Prediction of Slope Displacement Based on Wavelet Transform and Genetic Algorithm-Least Square Support Vector Machine[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 30(S2): 394-398)
(  0) 0) |
| [12] |
吕金虎, 陆君安, 陈士华. 混沌时间序列分析及其应用[M]. 武汉: 武汉大学出版社, 2001 (Lü Jinhu, Lu Jun'an, Chen Shihua. Chaotic Time Series Analysis and Its Application[M]. Wuhan: Wuhan University Press, 2001)
(  0) 0) |
| [13] |
龚祝平. 混沌时间序列的平均周期计算方法[J]. 系统工程, 2010, 28(12): 111-113 (Gong Zhuping. The Calculating Method of the Average Period Chaotic Time Series[J]. Systems Engineering, 2010, 28(12): 111-113)
(  0) 0) |
| [14] |
Cristianini N, Shawe-Taylor J. Introduction to Support Vector Machines[M]. Beijing: Electronic Industry Press, 2004
(  0) 0) |
| [15] |
曾勍炜, 徐知海, 吴键. 基于粒子群优化和支持向量机的电力负荷预测[J]. 微电子学与计算机, 2011, 28(1): 147-149 (Zeng Jingwei, Xu Zhihai, Wu Jian. Forecasting of Electricity Load Based on Particle Swarm Optimization and Support Vector Machine[J]. Microelectronics & Computer, 2011, 28(1): 147-149)
(  0) 0) |
2. Jiangsu Wanyuan Mapping Geographic Information Company Limited, 95 South-Tongguan Road, Lianyungang 222000, China
 2017, Vol. 37
2017, Vol. 37