2. 中国地震局地壳应力研究所武汉科技创新基地,武汉市洪山侧路40号,430071
奇异谱分析(singular spectrum analysis, SSA)是一种从时间序列的动力重构出发的无参自适应分析方法,无需先验信息[1]。其不仅能对信号的不同频率进行识别,还可以按照信号能量的大小进行严格排序,而且对非正弦波的周期信号同样可以稳定识别,比传统的频谱分析更具优势。SSA是一种适应面广、物理意义清晰、强化识别周期信号的广义功率谱分析方法[1-2],已被广泛用于气象学、海洋学等领域,近年来在大地测量学领域也有了初步的应用[3]。罗勇等[4]将SSA的去噪效果与EMD、小波分析进行对比,结果表明,SSA的去噪效果更优越且更稳定。将SSA应用于倾斜应变观测数据从理论上来讲是可行的,但还未有学者对其实际效果进行验证,本文将对此进行研究。
1 SSA基本原理 1.1 基本算法对于给定的一维时间序列x=(x1, x2, …,xN),SSA实现过程主要分为以下4个步骤:
1) 计算轨迹矩阵X。根据嵌入长度L计算给定时间序列的轨迹矩阵X, 轨迹矩阵X为L×K阶,其中K=N-L+1, 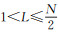
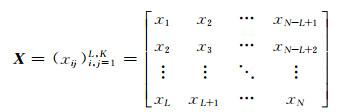
|
上述轨迹矩阵所有反对角线上的元素均相等,也称为Hankel矩阵。
2) 奇异值分解。定义矩阵C=XXT,XT为X的转置矩阵。计算矩阵C的特征值λi及特征向量Ui,按照降序将特征值排列,其特征值依次为λ1,λ2,…,λL且λ1≥λ2≥…≥λL≥0, 对应的特征向量为U1,U2,…,UL。设
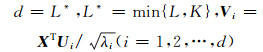
|
式中,Ui与Vi是轨迹矩阵的左右特征向量, 轨迹矩阵X可以由初等矩阵合成:
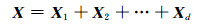
|
式中,初等矩阵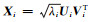
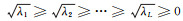
3) 分组。将初等矩阵Xi的下标(i=1, 2, …, d)分成p个不相交的子集I1, I2, …, IP,设I={i1, i2, …, im},则:
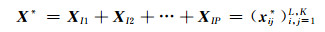
|
选取集合I1, I2, …, IP的过程即为分组。
4) 对角平均。得到的重构矩阵X*的反对角线上的元素已不相同,需进行对角平均[3],从而可以得到一个重构的时间序列s1, s2, …, sN。
1.2 嵌入维度L、重构阶次P以及重构成分的选取和判断SSA实现的过程需要确定两个重要参数——嵌入维度L和重构阶次P。嵌入维度L的选择直接影响SSA分解信号的效果,若嵌入维度L较小,将会导致信号分解不彻底;反之,将会使低频信号的分解产生谱裂现象[5]。倾斜应变观测数据的主要成分为固体潮,因此选取的嵌入维度L一般为固体潮周期的整数倍分解效果较好。重构阶次P的选择实际上为SSA的去噪过程,P过大会将噪声作为有用信号提取出来;P过小会将有用信号当作噪声剔除。确定P的常用方法为拐点法:噪声经过奇异值分解得到的奇异谱有着不同于有用信号的特点,即噪声的奇异值大小相当,奇异谱基本趋于平缓,出现噪声平台,此时奇异值的变化速率突降,产生拐点[6]。
根据SSA基本原理,SSA对周期成分的识别表现为奇异谱出现一对近似相等的奇异值,其序列号设为k和k+1,与之相对应的是一对正交的特征向量和一对正交的时间主成分。将第k个与k+1个主分量进行叠加重构,即得到一个周期震荡成分[5]。SSA对信号的分解是按照方差的大小进行主分量排序的,一般分解的主分量在频域上表现为从低频到高频,信号的振幅由大到小。Vautard等[5]认为,原始序列中若存在趋势,那么趋势分量应该出现在前几个主分量中,可用Kendall非参数检验进行判断。
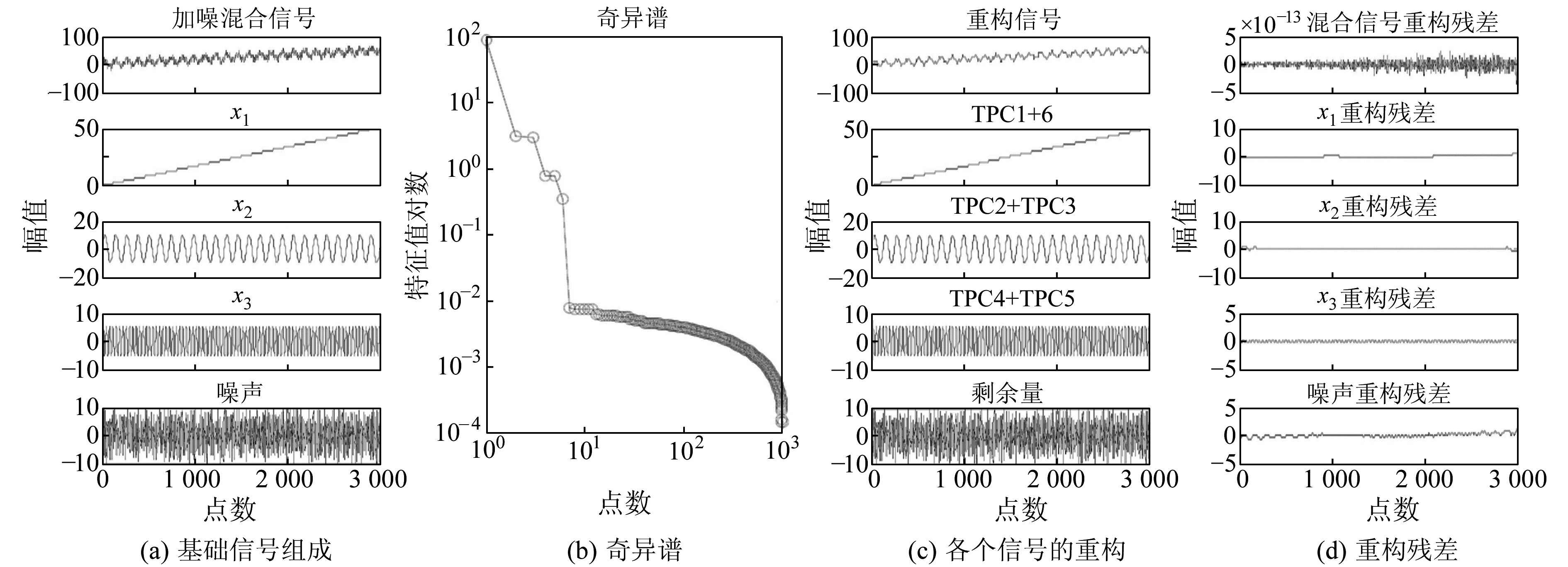
2 模拟数据实验 2.1 基础信号分解为了验证SSA在时间序列分析中的去噪、提取周期项和趋势项功能等的有效性,对下列由基础信号组成的混合模拟数据进行奇异谱分析:

|
式中,x1为趋势项,x2与x3为周期项,x4为均值为0、标准差为2的随机噪声。数据长度N为3 000。对上述模拟信号进行奇异谱分析,嵌入维度L=N/3。
图 1(a)为原始混合信号以及基本组成信号。图 1(b)为对加噪混合信号进行SSA后得到的奇异谱。从奇异谱可以看出,前6个奇异值相对其他奇异值大得多,经过计算可知,前6个主分量的方差贡献率高达99.85%,又因噪声的奇异谱趋于平缓的特性,由此可判断,若要达到去噪的目的,取前6个主分量进行重构即可。图 1(c)显示的是前6阶主分量重构的时间序列,结合图 1(b)可知,TPC1和TPC6组成了与趋势项x1吻合的信号,第2和第3个奇异值近似相等,应表现为一个周期震荡行为,因此将TPC2和TPC3进行叠加重构,得到了与x2一致的信号。同理可知,将TPC4和TPC5进行叠加,得到的信号与x3一致,其余的主分量组成剩余量,表示噪声成分。从各自的残差序列(图 1(d))来看,重构序列几乎完整地表达了原始信号的有效信息。其剩余量与原始序列中噪声的相关系数为0.998,可见SSA的去噪效果非常显著。
|
图 1 基础信号的SSA分解结果 Fig. 1 The SSA results of basic singal |
实际的观测数据中往往包含各种误差,因此要求在实际工作中使用的数据处理方法具备良好的稳定性。可以通过测试SSA对噪声的敏感程度来判断其稳定性:逐步增加§2.1中混合信号的噪声成分,判断SSA分离和识别基础信号的稳定性。
分别对混合信号加入噪声标准差S=0、2、5、7,图 2为得到的信号分解的结果。由图 2分解出的各个信号可以看出,未加噪的信号分解(图 2(a))与噪声S=2时的信号分解(图 2(b))效果相当,能清晰地将各个基础信号从混合信号中分离出来。当噪声S=5时,噪声的标准差与最小信号x3的振幅一致,此时在原始混合信号中x3被噪声湮没,但经过SSA处理之后,仍然能清晰辨识出x3(图 2(c))。将噪声增大至S=7时,噪声标准差高于信号x3的振幅,低于信号x2的振幅,此时得到的分解结果中,信号x3湮没在噪声中无法提取出来,而信号x2依然可以被提取出来。对不同的噪声背景下经过SSA处理之后重构信号x2与x3进行傅里叶分析发现,噪声从S=0增加至S=5,能稳定识别信号的频率和振幅,S=7时只能将x2分离出来。

|
图 2 不同噪声背景下混合信号的SSA分解结果 Fig. 2 The SSA results of mixed-signal in different noise |
上述分析表明,SSA的稳定性较好,当噪声标准差低于信号振幅时,信号能被正确识别,当噪声标准差高于信号振幅时,信号无法被正确识别。根据李瑞莎等[7]关于EMD的稳定性测试结果可知,当噪声标准差达到信号振幅的一半时,信号就已经湮没在噪声中无法分离出来。将其与上述SSA的稳定性测试结果进行对比后发现,SSA的稳定性要优于EMD,能有效提取微弱信号。
2.3 奇异点检测对观测资料中包含的各类干扰的识别与分离是目前形变学科研究和发现地震前兆信息的重要途径之一,因此有必要对SSA识别奇异点的能力进行测试。设x1为背景信号,在t=1 000和t=2 000处加入干扰信号x2,进行SSA处理后结果如图 3(b)所示,TPC1与TPC2重构了背景信号,TPC3与TPC4重构了干扰信号,通过原始混合信号与重构信号的傅里叶分析发现,二者的结果一致,再次验证了SSA识别周期信号的能力。从分解得到的剩余量(图 3(b))可以看出,在t=1 000和t=2 000附近产生了菱形鼓包现象,其变化的最大极值点即为t=1 000和t=2 000。结果表明,SSA能对突变点进行检测,有一定的识别干扰的能力。
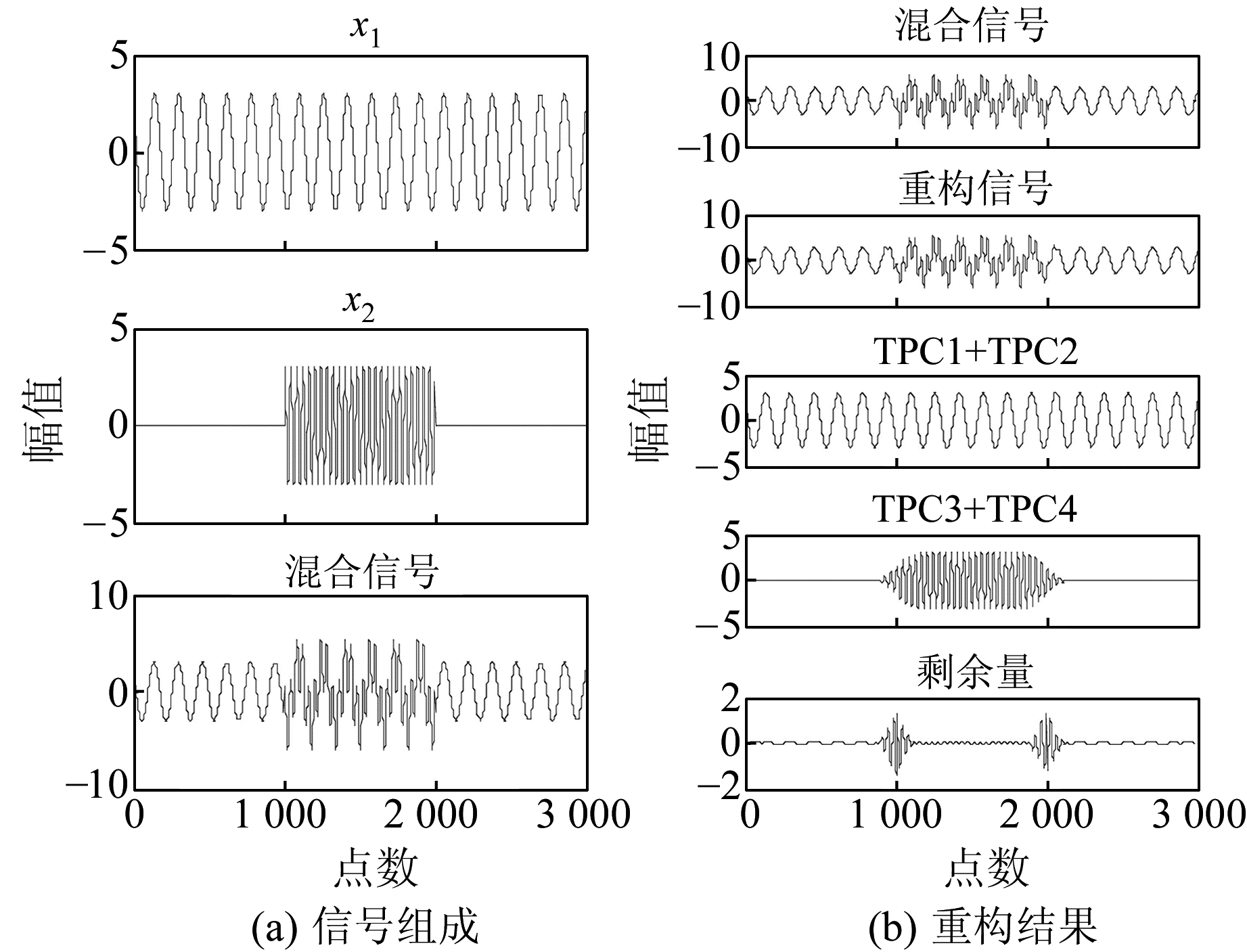
|
图 3 奇异点检测结果 Fig. 3 Singularity detection results |
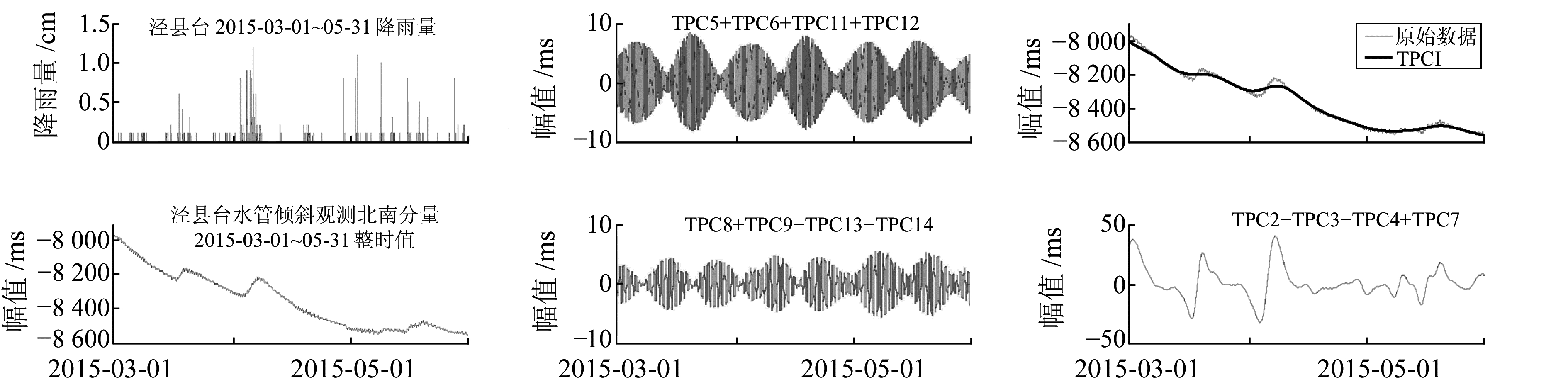
在固体潮的日常观测中,观测曲线除受特殊的地球物理事件(如地震)影响外,还可能受到各种其他因素的干扰,其中降雨可对观测数据的宏观趋势产生较大的影响,表现为使固体潮观测曲线产生大幅度的畸变。SSA对观测数据的处理能实现周期信号与非周期干扰的分解,降雨影响属于低频非周期干扰,一般会被分解到前几个TPC中。选取丹东台2010-04-01~2010-06-30的洞体应变东西分量观测数据、徐州台2014-07-01~2014-09-30分量钻孔应变北南分量观测数据以及泾县台2015-03-01~2015-05-31水管倾斜北南分量观测数据的整点值进行SSA处理,得到的结果如图 4~6所示。

|
图 4 丹东台SSA处理结果 Fig. 4 The SSA results of Dandong station |

|
图 5 徐州台SSA处理结果 Fig. 5 The SSA results of Xuzhou station |
|
图 6 泾县台SSA处理结果 Fig. 6 The SSA results of Jingxian station |
图 4为丹东台处理结果,选取的嵌入纬度L=128。由分解的结果可知,TPC1为趋势成分,描绘了原始数据的整体趋势方向。原始曲线在2010-05-04产生了较大的畸变,经查证为降雨引起的干扰。将TPC4与TPC5、TPC7与TPC8分别叠加重构,得到两组非常平稳的周期信号,经傅里叶变换后发现其周期分别约为12 h和24 h,代表了固体潮中半日波与日波的成分;将TPC2、TPC3、TPC6、TPC9叠加重构,发现该重构成分过滤掉了趋势项和周期信号,从而凸显了干扰成分,干扰影响的范围约为8 d。
图 5为徐州台处理结果,选取的嵌入维度L=160。徐州台7~9月由降雨导致的较严重的干扰有3处:2014-08-07、2014-08-24和2014-09-17。原始曲线由于漂移量大使得干扰产生的畸变不太明显,经过SSA处理后,得到的TPC1为趋势项,与原始曲线吻合较好;TPC2与TPC5叠加重构为干扰项,此时降雨产生的干扰由于去掉了漂移量而凸显出来,干扰影响的范围约为10~15 d;TPC3、TPC4、TPC8、TPC9叠加重构为半日波成分;TPC6与TPC7叠加重构为日波成分。
图 6为泾县台处理结果,选取的嵌入纬度L=160。徐州台3~5月由降雨导致的较严重的干扰有2处:2015-03-18和2015-04-05。从处理的结果来看,趋势项仍然是TPC1;TPC2、TPC3、TPC4、TPC7叠加重构为干扰项,凸显出2处比较大的降雨干扰,干扰影响的范围约为7~10 d;TPC5、TPC6、TPC11、TPC12叠加重构为半日波成分;TPC8、TPC9、TPC13、TPC14叠加重构为日波成分。
经过大量实际数据SSA处理验证,在处理倾斜应变观测数据时,嵌入维度为L=120~160时,基本可满足将趋势项、干扰项与周期项进行分离的要求。
4 结语1) SSA能将混合信号分解为各个基本信号的简单线性叠加,优先分离出能量较大的信号;SSA的稳定性优于EMD,能稳定提取微弱信号,去噪效果显著,对于低于信号振幅的噪声,能有效剔除;SSA能对突变点进行检测,有一定的识别干扰的能力;存在边缘误差问题。
2) 对丹东台、徐州台和泾县台倾斜应变观测数据进行SSA处理,有效提取了数据的趋势成分和固体潮潮波成分,且对数据中的干扰成分进行了有效分离,识别出周期为7~15 d的降雨干扰,对干扰排除和异常提取具有一定的参考意义。
3) 经过大量实际数据验证,在处理倾斜应变观测数据时,嵌入维度为L=120~160基本可满足将趋势项、干扰项与周期项进行分离的要求。
| [1] |
江志红, 丁裕国. 奇异谱分析的广义性及其应用特色[J]. 气象学报, 1998, 56(6): 736-745 (Jiang Zhihong, Ding Yuguo. Generality and Applied for Singular Spectrum Analysis[J]. Acta Meteorologica Sinica, 1998, 56(6): 736-745 DOI:10.3321/j.issn:0577-6619.1998.06.008)
(  0) 0) |
| [2] |
吴洪宝. 奇异谱和多通道奇异谱分析[J]. 气象教育与科技, 1997(4): 1-10 (Wu Hongbao. Singular Spectrum and Multichannel Singular Spectrum Analysis[J]. Meteorological Education and Science, 1997(4): 1-10)
(  0) 0) |
| [3] |
卢辰龙.奇异谱分析在大地测量时间序列分析中的应用研究[D].长沙: 中南大学, 2014 (Lu Chenlong.Research on Application of Singular Spectrum Analysis in Geodetic Survey Time Series[D]. Changsha: Central South University, 2014) http://cdmd.cnki.com.cn/Article/CDMD-10533-1014407784.htm
(  0) 0) |
| [4] |
罗勇, 匡翠林, 卢辰龙, 等. 基于SSA的GPS坐标序列去噪及季节信号提取[J]. 大地测量与地球动力学, 2015, 35(3): 391-395 (Luo Yong, Kuang Cuiling, Lu Chenlong, et al. GPS Coordinate Series Denoising and Seasonal Singnal Extraction Based on SSA[J]. Journal of Geodesy and Geodynamics, 2015, 35(3): 391-395)
(  0) 0) |
| [5] |
Vautard R, Yiou P, Ghil M. Singular-Spectrum Analysis: A Toolkit for Short, Noisy Chaotic Signals[J]. Physica D Nonlinear Phenomena, 1992, 58(1): 95-126
(  0) 0) |
| [6] |
Golyandina N. On the Choice of Parameters in Singular Spectrum Analysis and Related Subspace-Based Methods[J]. Statistics & Its Interface, 2011, 56(6): 736-745
(  0) 0) |
| [7] |
李瑞莎, 武艳强, 张希. 希尔伯特-黄变换方法在固体潮数据处理中的应用[J]. 地震研究, 2012, 35(1): 66-72 (Li Ruisha, Wu Yanqiang, Zhang Xi. Application of Hilbert-Huang Transform in Data Processing of Earth Tide Deformation[J]. Journal of Seismological Research, 2012, 35(1): 66-72 DOI:10.3969/j.issn.1000-0666.2012.01.012)
(  0) 0) |
2. Wuhan Base of Institute of Crustal Dynamics, CEA, 40 Hongshance Road, Wuhan 430071, China
 2017, Vol. 37
2017, Vol. 37


