2. 武汉理工大学资源与环境工程学院,武汉市珞狮路122号,430070;
3. 东华理工大学江西省数字国土重点实验室,南昌市广兰大道418号,330013;
4. 武汉市测绘研究院博士后创新实践基地,武汉市万松园路209号,430022
目前对变形及滑坡的监测主要是基于GPS和全站仪,虽然精度较高,但只能实现单点的监测,无法实现区域的监测。针对此,出现了基于三维激光扫描技术的测量手段,该技术具有高空间分辨率的扫描特点,可以实现对某个区域的监测。毕俊等[1]利用隧道内部的点云数据进行断面分析,获得了隧道的收敛变形分析。邢正全等[2]利用Trimble GX 3D激光扫描系统对某边坡进行扫描,获得了边坡位移监测结果。黄晓阳等[3]对获取的井架点云数据进行噪声剔除后,利用平面拟合方法实现了井架倾斜变形分析。谢谟文等[4]将三维激光扫描技术应用到滑坡表面的监测,并将监测结果与GIS平台结合起来,实现了对边坡稳定性的评价。姚艳丽等[5]利用三维激光扫描技术获得滑坡表面变形资料,并将这些变形资料与灰色模型进行组合,实现了对边坡位移的预测。栾元重等[6]利用三维激光扫描技术对跨海大桥进行三维变形监测,并与测量机器人结果进行对比分析发现,两者误差不超过0.5 mm,验证了三维激光扫描技术应用于变形监测的可行性。文献[7-9]将获取的点云数据进行DEM模型重构,并对不同时序的DEM进行对比分析,获得了一维状态下的变形结果。Aryal等[10]对不同时序的点云数据,利用PIV方法进行估计,获得了二维变形监测结果。Monserrat等[11]充分利用不同时序点云数据的旋转和平移参数,获取了基于三维激光点云的三维变监测结果。
以上学者虽然对三维激光技术应用于变形监测进行了研究,并利用各种方法提取了变形分析结果,但只单纯地对点云或点云模型重构结果进行对比分析,并没有分析点云误差对点云对比分析的结果。为此,本文对三维激光扫描的测距、测角及配准误差进行分析,给出点云误差模型,并将其转换为误差椭球,通过计算相邻误差椭球,确定实际点云误差椭球。最后,利用误差椭球中半轴长度和点位误差极限值的关系,给出变形可监测性指标,并通过实例验证了本文方法的可行性。
1 点云误差模型 1.1 点位误差模型假设三维激光扫描极坐标系统中的点坐标为(ρi, θi, φi),其中,ρi、φi和θi分别为三维激光扫描的测距、水平角和垂直角。在三维激光扫描过程中,获取的是目标物的三维坐标,该坐标系统由极坐标计算得到:
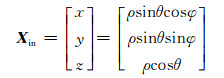
|
(1) |
式中,根据误差传播规律得到协方差矩阵为:
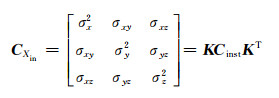
|
(2) |
式中,
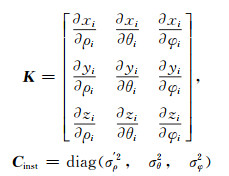
|
(3) |
式中,测距方差受入射角α的影响[12]:

|
(4) |
式中,入射角α被定义为激光波束向量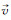
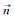
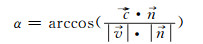
|
(5) |
三维激光点位误差不仅受测距、测角误差的影响,还受激光光斑的影响。理论上激光波束是沿着激光光斑中心方向,但实际上激光波束很难完全沿着波束中心发射。在考虑激光波束区域服从高斯分布的情况下,光斑中点位误差标准差为[14]:

|
(6) |
式中,L和l分别是激光光斑的长轴和短轴,将其分解到水平和垂直方向,如图 1所示。

|
图 1 光斑长轴和短轴的分解 Fig. 1 Decomposition of major and minor axis of spot |
通过以上分析,确定三维激光扫描点位误差为测距、测角和激光光斑误差之和。由式(2)和式(6)可以确定每个三维激光扫描中每个激光点的协方差为:
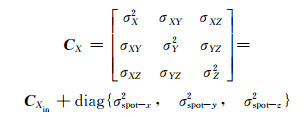
|
(7) |
将三维激光扫描点云配准到全局坐标系统:
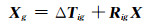
|
(8) |
式中,X=[X Y Z]T为三维激光扫描系统中的坐标向量;Xg=[Xg Yg Zg]T为配准后全局坐标系统中的坐标向量;ΔTig=[ΔX ΔY ΔZ]为从扫描系统到配准后坐标系统的平移向量;Rig为旋转变量。
根据以上参数得出,配准后的点位协方差为:

|
(9) |
式中,Cpg=diag(σΔX2 σΔY2 σΔZ2 σα12 σα22 σα32)为配准过程中的转换参数,α1、α2、α3为旋转角,
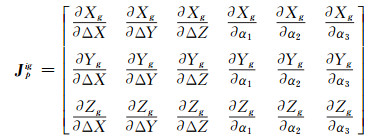
|
(10) |
在三维情况下,点位误差空间不确定性可以采用误差椭球的形式,由式(9)可知点位误差分布为:
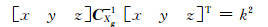
|
(11) |
式中,k为尺度参数。式(10)定义了三维误差椭球的基本形式,利用正交矩阵对角化CXg,则存在正交矩阵满足QTCXgQ=Λ,Λ是对角矩阵CXg的3个特征值。利用Q对测量点的误差椭球进行旋转和平移,得到正交矩阵,则式(11)写为[15]:
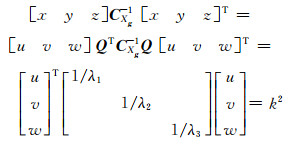
|
(12) |
式(12)可写为:

|
(13) |
式中,λ1、λ2和λ3是CXg的特征值。
由式(13)可知,点位分布的概率由尺度参数k确定。k=1时,点位分布概率为19.87%;k=2时,点位分布概率为73.85%,此时误差椭球基本上包含了大部分的误差信息,因此最终确定用于描述点位误差椭球大小的尺度参数为k=2。
三维激光扫描过程中,由于采集大量密集的点,所以相邻点之间存在误差椭球的重叠。为了估计真实的点云误差椭球,需要消除相邻误差椭球的交集,假设在y轴方向存在交集,则相邻误差椭球形式为:
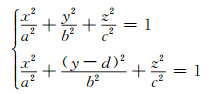
|
(14) |
式中,d为扫描间隔。相邻点位误差椭球的交集体积为:

|
(15) |
假设在扫描点云过程中,存在m行和n列个点,则y轴上存在相邻误差椭球交集的数量为n(m-1)。因此,整个重叠区域的体积为:
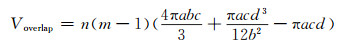
|
(16) |
在不考虑相邻误差椭球交集的情况下,整个点云误差椭球的体积为:
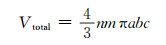
|
(17) |
则实际点云误差椭球体积表示为:

|
(18) |
以上是假设在y轴上存在椭球交集,如果在x、z轴上存在交集,则按照相同的方法进行计算。
3 点云变形可监测性指标的确定三维激光扫描最小变形可监测性指标的确定将直接决定其变形监测的能力,而最小变形可监测性指标是由点云误差引起的,因此可根据实际点云误差椭球确定可监测性指标。根据计算得到实际点云误差椭球及总的点数后,便可确定单个点的点位误差椭球为:
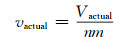
|
(19) |
在不考虑相邻点位误差椭球交集影响的前提下,实际的单个点点位误差椭球体积为:
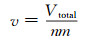
|
(20) |
在考虑和不考虑相邻误差椭球交集影响的情况下,点位误差椭球体积都发生了改变,从而其所对应的点位协方差也会发生变化。假设在考虑相邻误差椭球交集影响的前提下其点位协方差为C′Xg,不考虑相邻误差椭球交集影响的前提下其点位协方差为CXg,C′Xg与CXg之间存在尺度参数l,则有:
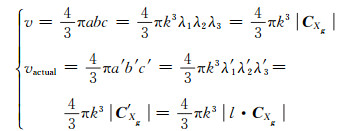
|
(21) |
式中,a′、b′、c′为考虑相邻误差椭球交集相互影响情况下实际点位误差椭球半长轴的大小,λ′1、λ′2、λ′3为C′Xg的特征值。
根据式(21)得到尺度参数l为:
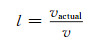
|
(22) |
根据尺度参数可得到实际点位协方差C′X为:

|
(23) |
假设实际点位协方差C′X表示的3×3矩阵为:

|
(24) |
则实际点位误差标准差为:
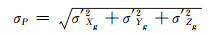
|
(25) |
根据误差极限性质,点位误差限差为:

|
(26) |
式中,k=2。则变形可监测性指标大小为:
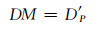
|
(27) |
本文利用Riegl-VZ400扫描仪对某滑坡及其边坡进行扫描。利用木板模拟滑坡(图 2),木板高度为0.05 m,即滑坡在垂直方向上的大小为0.05 m。

|
图 2 模拟的滑坡 Fig. 2 Simulating landslide |
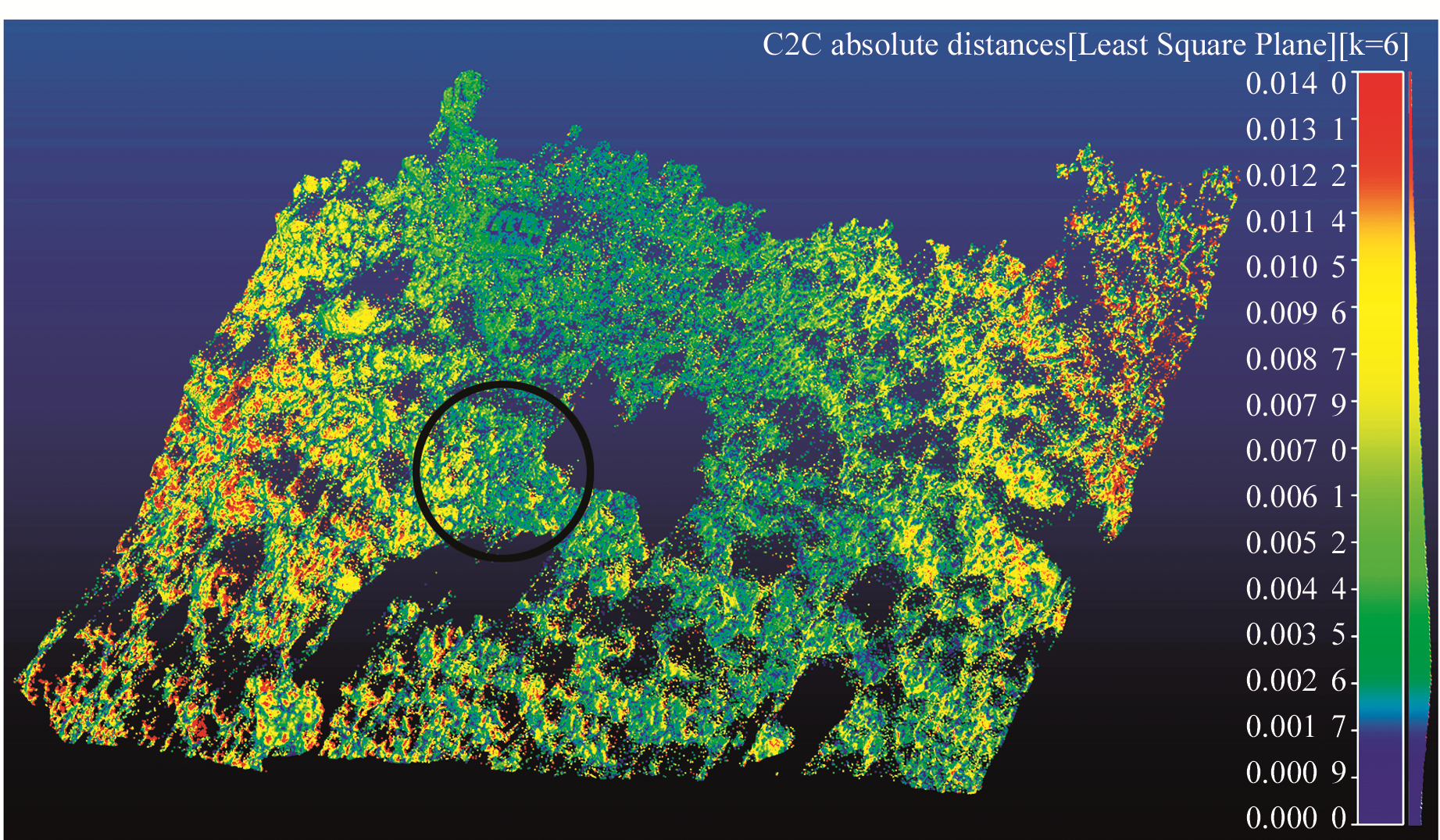
为验证本文计算变形可监测性指标大小的正确性,在2015-10对边坡进行重复扫描,并利用KNNS[16]提取扫描重合误差,结果见图 3(单位m)。利用本文方法计算得到变形可监测性指标为0.014 3 m,即只有在变形大于0.014 3 m时才能被监测出来,小于0.014 3 m的变形可能被点云误差掩盖掉。而由图 3可知,由点云误差引起的点云重合度误差为0.014 m,与计算的变形可监测性指标非常接近,从而验证了本文方法的准确性。图 3中间黑色圆形区域出现了较大黑洞,原因是前方较高的土石方挡住了激光射线。
|
图 3 重合度误差 Fig. 3 The overlapping error |
在2015-12对边坡进行第二次扫描,并提取变形值,结果见图 4(单位m)。图中,矩形方框为提取的模拟滑坡值,椭圆形和圆形区域为主要的滑坡区域,而最大的滑坡区域发生在最顶端,造成该现象的原因是顶部最容易受降雨的冲蚀。中部的圆形区域给出了滑坡的方向,中间靠左区域也出现了滑坡,同时比图 3黑色圆圈中对应位置的黑洞明显变小。造成该现象的原因是前方较高的土石方在雨水的冲刷下出现了滑落,从而不会遮挡更多的激光射线。由图 4右边计算的变形标记可以看到,计算得到的最大变形量为0.383 9 m,而在图 4中出现的大部分蓝色区域分为两个主要区域的数值范围,如图中右下角矩形方框中所示。第一区域点云对比偏差在0.014 m以内,主要是由测距、测角、光斑及配准误差引起的,并不是真正的变形;第二区域点云对比偏差主要在0.036 m附近,该区域主要是模拟的滑坡区域,而模拟的实际滑坡大小是0.05 m,计算得到滑坡大小与实际滑坡大小相差0.014 m,而该大小正好与点云误差引起的重合度误差相同,从而进一步验证了本文算法的可靠性。由图5中颜色的区分可以很轻易地确定滑坡区域,从而证明了三维激光扫描用于区域变形监测的优势。

|
图 4 变形提取结果 Fig. 4 The result of deformation extraction |
本文通过分析影响点云误差的测距、测角、光斑及配准误差,给出了点云误差模型,并推导了配准后全局坐标系统下的点云误差模型;利用协方差将其转为点云误差椭球,通过计算相邻误差椭球之间的交集状况,推导实际点云误差椭球大小;利用误差椭球中半轴长度和点位误差极值的关系,实现三维激光扫描最小变形可监测量,从而确定变形可监测性指标大小。利用不同测站对没有发生滑坡的边坡进行重复扫描,计算点云重合度误差,同时利用本文方法计算变形可监测性指标,最终确定点云重合度误差与变形可监测性指标基本相同,从而验证了本文方法的有效性。同时对实际发生滑坡的边坡进行扫描,提取了发生滑坡的区域,并对滑坡的方向进行分析,利用变形可监测性指标给出可能没有发生或无法探测出变形的区域。通过对模拟滑坡和实际滑坡进行综合分析,确定变形可监测性指标对基于三维激光扫描的变形监测具有指导作用。
| [1] |
毕俊, 冯琰, 顾星晔, 等. 三维激光扫描技术在地铁隧道收敛变形监测中的应用研究[J]. 测绘科学, 2008, 33(增2): 14-16 (Bi Jun, Feng Yan, Gu Xingye, et al. The Application of Subway Tunnel Convergence Deformation Monitor Based on Three-Dimensional Laser Scanner[J]. Science of Surveying and Mapping, 2008, 33(S2): 14-16)
(  0) 0) |
| [2] |
邢正全, 邓喀中. 三维激光扫描技术应用于边坡位移监测[J]. 地理空间信息, 2011, 9(1): 68-71 (Xing Zhengquan, Deng Kazhong. Application of 3D Laser Scanning Technology in Slope Displacement Monitoring[J]. Geospatial Information, 2011, 9(1): 68-71 DOI:10.3969/j.issn.1672-4623.2011.01.023)
(  0) 0) |
| [3] |
黄晓阳, 栾元重, 闫勇, 等. 基于三维激光扫描测量技术的井架变形观测[J]. 工程勘察, 2012, 4(1): 66-69 (Huang Xiaoyang, Luan Yuanzhong, Yan Yong, et al. Monitoring Deformation of Headframe Based on 3D Terrestrial Laser Scanner[J]. Geotechnical Investigation & Surveying, 2012, 4(1): 66-69)
(  0) 0) |
| [4] |
谢谟文, 胡嫚, 王立伟. 基于三维激光扫描仪的滑坡表面变形监测方法——以金坪子滑坡为例[J]. 中国地质灾害与防治学报, 2013, 24(4): 85-92 (Xie Mowen, Hu Man, Wang Liwei. Landslide Monitoring by Three-Dimensional Laser Scanner-Case Study of the Displacement Detection of the Jinpingzi Landslide (Southwest China)[J]. Chinese Journal of Geological Hazard and Control, 2013, 24(4): 85-92)
(  0) 0) |
| [5] |
姚艳丽, 蒋胜平, 王红平. 基于地面三维激光扫描技术的滑坡模型监测与预测[J]. 测绘科学, 2014, 39(11): 42-47 (Yao Yanli, Jiang Shengping, Wang Hongping. Landslide Model Monitoring and Forecast by Using Ground 3D Laser Scanner[J]. Science of Surveying and Mapping, 2014, 39(11): 42-47)
(  0) 0) |
| [6] |
栾元重, 栾亨宣. 桥梁变形监测数据小波去噪与Kalman滤波研究[J]. 大地测量与地球动力学, 2015, 35(6): 1 041-1 046 (Luan Yuanzhong, Luan Hengxuan. Research on Wavelet Denoising and Kalman Filter in Bridge Deformation Monitoring Data[J]. Journal of Geodesy and Geodynamics, 2015, 35(6): 1 041-1 046)
(  0) 0) |
| [7] |
Oppikofer T, Jaboyedoff M, Blikra L, et al. Characterization and Monitoring of the Åknes Rockslide Using Terrestrial Laser Scanning[J]. Natural Hazards and Earth System Science, 2009, 9(3): 1 003-1 019 DOI:10.5194/nhess-9-1003-2009
(  0) 0) |
| [8] |
Abellán A, Vilaplana J M, Calvet J, et al. Rock Face Monitoring by Terrestrial Laser Scanning-Change Detection and Spatial Prediction of Rockfall[J]. Geomorphology, 2010, 119(3): 162-171
(  0) 0) |
| [9] |
Dangrbauer A, Paar G, Kaltenböck A. Geo-Information for Disaster Management[M]. Berlin Heidelberg: Springer, 2005
(  0) 0) |
| [10] |
Aryal A, Brooks B A, Reid M E, et al. Displacement Fields from Point Cloud Data: Application of Particle Imaging Velocimetry to Landslide Geodesy[J]. Journal of Geophysical Research:Earth Surface, 2012, 117(F1)
(  0) 0) |
| [11] |
Monserrat O, Crosetto M. Deformation Measurement Using Terrestrial Laser Scanning Data and Least Squares 3D Surface Matching[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2008, 63(1): 142-154 DOI:10.1016/j.isprsjprs.2007.07.008
(  0) 0) |
| [12] |
Grant D, Bethel J, Crawford M. Point-to-Plane Registration of Terrestrial Laser Scans[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2012, 72: 16-26 DOI:10.1016/j.isprsjprs.2012.05.007
(  0) 0) |
| [13] |
Soudarissanane S, Linenbergh R, Menenti M, et al. Scanning Geometry: Influencing Factor on the Quality of Terrestrial Laser Scanning Points[J]. Journal of Photogrammetry and Remote Sensing, 2011, 66(4): 389-399 DOI:10.1016/j.isprsjprs.2011.01.005
(  0) 0) |
| [14] |
Schaer P, Skaloud J, Landtwing S, et al. Accuracy Estimation for Laser Point Cloud Including Scanning Geometry[C]. Mobile Mapping Symposium, Pavoda, 2007 https://infoscience.epfl.ch/record/116146
(  0) 0) |
| [15] |
Du Z C, Wei Y F, Yao Z Q. Accuracy Analysis of Laser Radar Measurement System Based on Error Ellipsoid Model[J]. Journal of Shanghai Jiaotong University, 2009, 43(12): 1 881-1 885
(  0) 0) |
| [16] |
Abellan A, Jaboyedoff M, Oppikofer T, et al. Detection of Millimetric Deformation Using a Terrestrial Laser Scanner: Experiment and Application to a Rockfall Event[J]. Nature Hazards and Earth System Sciences, 2009, 9(2): 365-472 DOI:10.5194/nhess-9-365-2009
(  0) 0) |
2. School of Resource and Environment Engineering, Wuhan University of Technology, 122 Luoshi Road, Wuhan 430070, China;
3. Key Laboratory for Digital Land and Resources of Jiangxi Province, East China University of Technology, 418 Guanglan Road, Nanchang 330013, China;
4. Postdoctors Innovation and Practice Base of Wuhan Geomatics Institute, 209 Wansongyuan Road, Wuhan 430022, China
 2017, Vol. 37
2017, Vol. 37

