隧道围岩位移时间序列受岩土结构、自然环境、施工技术、自身物理变化等因素影响,呈现出非线性和非平稳的特点[1-3]。有效控制围岩位移对隧道工程建设和工后安全运营具有重要意义,也是高速公路、高速铁路建设所面临的重大课题。提高围岩位移预测精度是实现有效控制围岩位移的前提和保障。目前围岩位移的预测方法有:复变理论分析法、灰色理论、神经网络、支持向量机、时间序列分析方法等,这些方法均取得了较好的预测效果, 但也存在模型结构复杂或预测精度不高等问题。本文在已有研究方法的基础上,提出了加权复合分位数自回归模型的预测新方法,该方法具有模型结构简单、可操性强、拟合预测精度高等优点。实例分析验证了本文方法的有效性和优越性。
1 加权复合分位数自回归模型 1.1 加权分位数自回归模型分位数回归估计是一种全面数据统计分析方法[4],具有很强的抗干扰能力和稳健性,且对模型残差项无任何要求,在回归过程中能够保留变量之间的大部分信息。
随机变量Yt的p阶自回归AR(p)模型为:

|
(1) |
式中,θ=[θ1, θ2, …, θp]为自回归参数,ξt为随机误差项,Yt(t=1, 2, …, n)为因变量。
设FYt|(Yt-1,Yt-2,…,Yt-p)(y),t≥p+1是在随机变量(Yt-1, Yt-2, …, Yt-p)下Yt的条件分布函数,则Yt的第τ∈(0, 1)个条件分位数为:
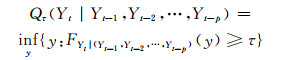
|
(2) |
式中,inf(·)为下确界函数。
在(Yt-1, Yt-2, …, Yt-p)(t≥p+1)下,Yt的τ条件分位数为Yt-1,Yt-2,…,Yt-p的线性函数,即Qτ(Yt|Yt-1, Yt-2, …, Yt-p)=θ1Yt-1+θ2Yt-2+…+θpYt-p,则系数向量θ(τ)的τ分位数估计值为:

|
(3) |
式中,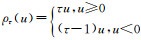
分位数回归估计式(3)等价于:

|
(4) |
显然,分位点τ不同时,估算出的模型参数也不同,因而可以得到不同的回归方程。
为了增强分位数回归的稳健性,降低模型厚尾误差对模型参数估计的影响[5],并使分位数回归估计方法的统计性质(主要是指方差和渐近性)稳定有效,本文通过对损失函数加权(对异常值赋予较小的权值)来应对可能出现的问题。这种加权分位数回归方法较经典分位数回归方法更加稳健,所估算出的模型参数更接近理想值,从而提高了模型的预测精度。
对式(3)中损失函数加权后得到模型参数的τ分位数估计值为:

|
(5) |
式中,n为建模样本数,权函数为[6]:

|
(6) |
式中,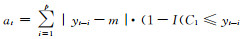
复合分位数回归[7-8]是各个分位点下分位数回归的综合表示。该回归方法的参数估计结果是各分位点下分位数回归参数估计结果的综合,具有唯一性,克服了传统分位数回归估算出的系数因分位点不同而取值不同的缺陷,使参数估计结果更具稳定性。具体过程如下。
设有一组分位点0<τ1<τ2<…<τk<1,记τ=(τ1, τ2, …, τk),则参数向量θ(τ)的加权复合分位数估计值为:

|
(7) |
显然,θ=[θ1, θ2, …, θp]的估计值是给定的一组分位点分位数回归的综合计算结果。
1.3 模型参数求解由于加权复合分位数回归计算比较复杂,不宜采用线性规划求解,又由于式(7)中的损失函数非光滑,这使得加权复合分位数回归的计算变得较困难。为解决此问题,可采用模拟退火算法(simulated annealing,SA)求参数的最优解。模拟退火算法[9-10]是源于物理中固体物质的退火过程与一般优化问题之间的相似性而开发的一种智能寻优算法。该算法具有概率突跳的能力,能够有效地避免搜索过程中陷入局部极小解,从而能在一个给定的空间内搜寻到问题的最优解。另外,该算法在搜索计算中不要求目标函数满足光滑可微性。模拟退火算法基本计算过程如下:
1) 初始化。给定初始温度T0及初始解θ,计算解对应的目标函数值f(θ),在本文中θ是模型的参数向量。
2) 模型扰动产生新解θ′,并计算对应的目标函数值f(θ′)。
3) 计算函数差值Δf=f(θ′)-f(θ)。
4) 如果Δf≤0,则接受新解作为当前解。
5) 如果Δf>0,则以概率p=e-(f(θ′)-f(θ))/(KT)(K为物理学中的Boltzmann常数, T为温度值)接受新解。
6) 对当前温度T值降温,对步骤2)~5)迭代N次。
7) 如果满足终止条件,输出当前解为最优解,结束算法;否则,降低温度,继续迭代。
需要指出的是,上述算法可以在MATLAB模拟退火算法工具箱内完成,使用该工具箱简单方便且高效。
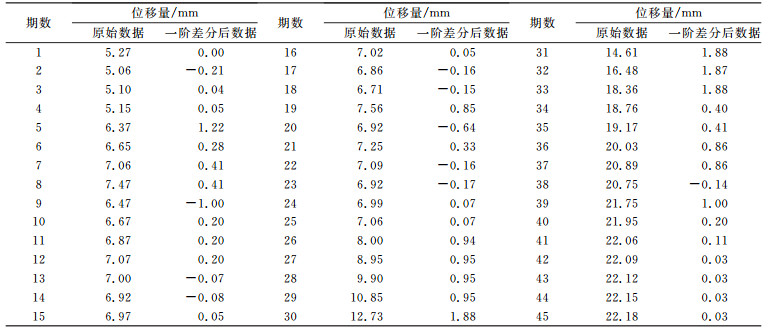
2 工程实例计算与分析昆明市阳宗隧道是一座单向分离式大断面隧道,全长2 725 m,最大埋深141 m,围岩类型主要是Ⅱ类及Ⅲ类,以玄武岩和灰岩为主[11]。本文采用昆明市阳宗隧道XK38+725断面的45个实测围岩变形数据进行计算分析,数据如表 1所示。
2.1 自回归AR(2)模型的确定首先,检验序列的平稳性。表 1中原始数据列的单位根检验统计量对应的p=0.999>0.05,stat=3.686 2,cValue=-1.947 2,可判断该序列为非平稳序列[12]。
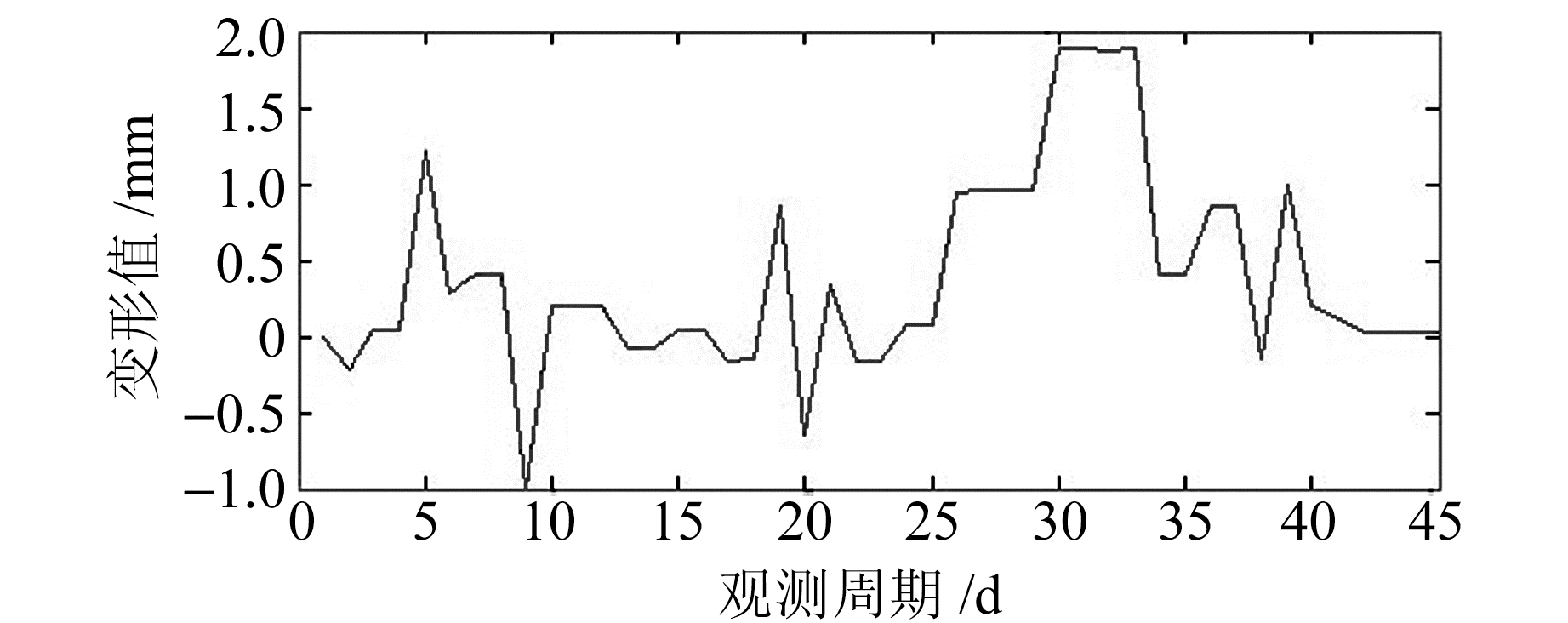
然后,对原始序列进行一阶差分计算(计算结果见表 1),并对差分数列进行平稳性和白噪声检验。平稳性检测p=0.004 326 8≪0.05,所以一次差分后序列归于平稳;一阶差分后白噪声检测p=8.299 5×10-7,表明该时间序列为非白噪声序列。一阶差分之后序列的时序如图 1所示。
|
图 1 一阶差分后序列图 Fig. 1 The first order differential posterior sequence diagram |
最后,采用ARMA模型来拟合差分后的平稳非白噪声序列的发展,借此提取该序列的有用信息。在使用此类模型之前需对模型定阶,即确定模型ARMA(p, q)中p和q。采用相对最优模型识别法[13]计算p和q均小于等于5时ARMA(p, q)的所有组合的BIC(贝叶斯信息准则)信息量,取其中BIC信息量达到最小的模型阶数。在所得的6行6列矩阵中(元素为BIC值),当p=2、q=0时,BIC取最小值79.106 9,所以确定AR(2)为最终预测模型。
2.2 模拟退火算法求参数最优解取表 1一阶差分处理后的前39个数据样本组成训练集,后6个数据样本组成测试集。首先设定5个分位点τ=[0.1, 0.3, 0.5, 0.7, 0.9],按式(7)定义适应度函数(目标函数):
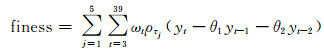
|
(8) |
式中,yt(t=1, 2, …, 39)来自训练集。利用MATLAB编写适应度函数的计算程序(函数名finess.m,程序在此略去),在计算ωt时可采用MATLAB统计工具箱里的函数prctile[14]确定25%和75%分位数的值。
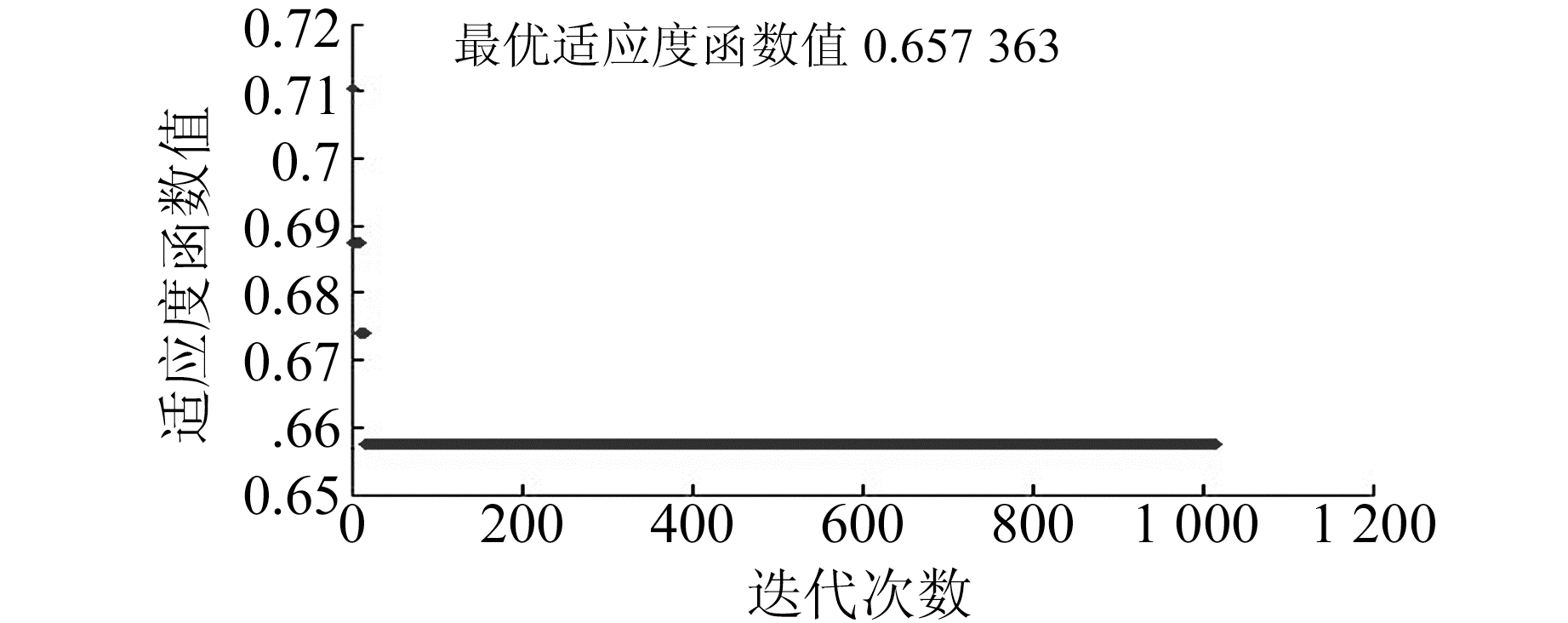
模拟退火算法中取参数搜索范围为[-1, 1],参数的初始值为θ0=[0.1, 0.8]。在MATLAB命令窗口用optimtool(‘simulannealbnd’)打开模拟退火算法的GUI,在Objective function输入@finess,在Start point输入[0.1, 0.8],在Bounds的Lower输入参数下限向量[-1, -1],在Upper输入参数上限向量[1, 1],其他参数取默认值。点击Start执行运算,经过1 033迭代输出的参数值为θ=[0.200 626 794 885 624, 0.219 426 216 708 682],经四舍五入后取θ1=0.200 6,θ2=0.2194。适应度函数的变化过程如图 2所示。
|
图 2 适应度函数迭代变化图 Fig. 2 Iteration map of fitness function |
将参数值代入式(1),得到AR(2)模型:
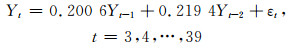
|
(9) |
经过逆推得到原始变形数据列的拟合模型为:
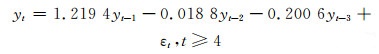
|
(10) |
模型(10)的决定系数R2=0.991 2,调整的决定系数R2=0.991 0,均方误差MES=0.357 9。说明模型拟合效果显著,精度很高,可以用于隧道围岩变形预测分析。
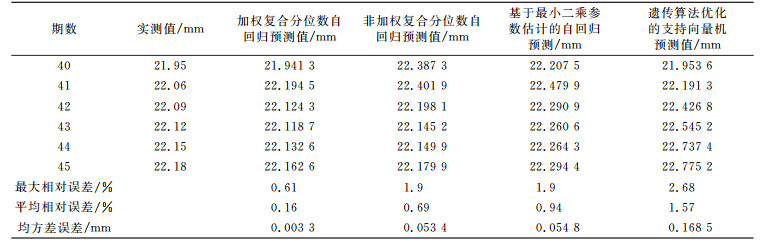
2.3 模型预测与分析比较用模型(10)预测后6期变形数据,将预测值与实际测量值进行比较,结果如表 2所示。作为对比,表 2还列出了非加权复合分位数自回归、基于最小二乘参数估计的自回归及文献[11]基于遗传算法优化的支持向量机的预测结果。
|
|
表 2 测试数据样本预测结果及比较 Tab. 2 Test data sample prediction results and comparison |
从表 2看出,加权复合分位数自回归的预测精度明显高于非加权复合分位数自回归的预测精度,说明前者的预测结果更接近实际值,而这两种预测方法的预测精度均高于基于最小二乘参数估计的自回归和基于遗传算法优化的支持向量机的预测精度。预测结果分析表明,加权复合分位数自回归预测模型改进了复合分位数自回归预测模型,改进后的预测模型在应对波动较大的数据点时稳健性更强。
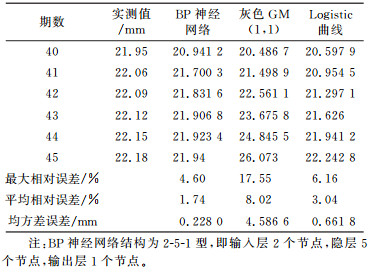
采用相同的建模样本集(前39期数据样本)和测试样本集(后6期数据样本),分别建立BP神经网络、灰色GM(1, 1)、Logistic曲线模型,并对后6期的围岩变形进行预测,预测结果见表 3。相应的曲线模型如下。
|
|
表 3 几种常见模型的预测结果及误差分析 Tab. 3 Prediction results and error analysis of several common models |
灰色GM(1, 1)模型:

|
(11) |
Logistic曲线模型:
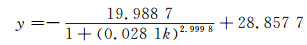
|
(12) |
显然,表 3给出的BP神经网络、灰色GM(1, 1)模型和Logistic曲线模型的预测精度低于加权复合分位数自回归模型,说明本文方法在时间序列预测方面具有一定的优势,值得工程技术人员借鉴。
3 结语加权分位数回归是指对分位数回归的损失函数加权,权函数仅受监测数据驱动,这种加权起到对模型残差的调节作用,抑制了离群数据点对模型参数估值精准性的干扰,提升了分位数回归估计的稳健性。在此基础上形成的加权复合分位数估计具有更强的稳健性和数据适应能力,且对模型残差无任何要求。工程实例表明,用基于加权复合分位数参数估计的自回归AR(p)模型处理非线性、非平稳的隧道围岩变形数据完全可行。从对后期变形值的预测精度来看,所建模型具有很强的外推能力,预测效果优于非加权复合分位数估值的自回归AR(p)模型和其他一些常用的预测模型。
| [1] |
张玥.隧道施工智能管理系统研究及形象进度系统实现[D].西安: 长安大学, 2012 (Zhang Yue.Research on Intelligent Management System of Tunnel Construction and Implementation of Image Processing System[D]. Xi'an: Chang'an University, 2012) http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D235110
(  0) 0) |
| [2] |
董辉.基于支持向量机的岩土非线性变形行为预测研究[D].长沙: 中南大学, 2007 (Dong Hui.Nonlinear Deformation Behavior Prediction of Rock and Soil Based on Support Vector Machine[J]. Changsha: Central South University, 2007) http://cdmd.cnki.com.cn/Article/CDMD-10533-2008166224.htm
(  0) 0) |
| [3] |
岳顺.隧道围岩动力稳定性研究与时间序列建模分析[D].重庆: 重庆大学, 2009 (Yue Shun. Study on Dynamic Stability and Time Series Modeling of Tunnel Surrounding Rock[D]. Chongqing: Chongqing University, 2009) http://cdmd.cnki.com.cn/article/cdmd-10611-2009148399.htm
(  0) 0) |
| [4] |
Paren E. Quantile Probability and Statistical Data Modeling[J]. Statistical Science, 2004, 19(4): 625-662
(  0) 0) |
| [5] |
解其昌. 分位数回归方法及其在金融市场风险价值预测中的应用[M]. 北京: 中国农业科学技术出版社, 2014 (Xie Qichang. Quantile Regression Method and Its Value in the Financial Market Risk Prediction Application[M]. Beijing: Chinese Agricultural Science and Technology Press, 2014)
(  0) 0) |
| [6] |
施安成.自回归时间序列的加权分位数方法[D].合肥: 中国科学技术大学, 2014 (Shi Ancheng. Weighted Quantile Method for Autoregressive Time Series[D]. Hefei: University of Science and Technology of China, 2014) http://cdmd.cnki.com.cn/Article/CDMD-10358-1014300046.htm
(  0) 0) |
| [7] |
Zou H, Yuan M. Composite Quantile Regression and the Oracle Model Selection Theory[J]. Annals of Statistics, 2008, 36(3): 1 108-1 126
(  0) 0) |
| [8] |
刘晓倩, 周勇. 加权复合分位数回归方法在动态VaR风险度量中的应用[J]. 中国管理科学, 2015, 23(6): 1-8 (Liu Xiaoqian, Zhou Yong. Application of Weighted Quantile Regression in Dynamic VaR Risk Measurement[J]. Chinese Journal of Management Science, 2015, 23(6): 1-8)
(  0) 0) |
| [9] |
许国根, 贾瑛. 模式识别与智能计算的MATLAB实现[M]. 北京: 北京航空航天大学出版社, 2012 (Xu Guogen, Jia Ying. MATLAB Implementation of Pattern Recognition and Intelligent Computing[M]. Beijing: Beihang University Press, 2012)
(  0) 0) |
| [10] |
史峰, 王辉, 郁磊, 等. MATLAB智能算法30个案例分析[M]. 北京: 北京航空航天大学出版社, 2012 (Shi Feng, Wang Hui, Yu Lei, et al. 30 Cases of MATLAB Intelligent Algorithm[M]. Beijing: Beihang University Press, 2012)
(  0) 0) |
| [11] |
陈桦深.基于支持向量机的隧道围岩位移变形预测分析研究[D].重庆: 重庆交通大学, 2015 (Chen Huashen.Study on Displacement and Deformation Prediction of Tunnel Surrounding Rock Based on Support Vector Machine[J]. Chongqing: Chongqing Jiaotong University, 2015) http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2808760
(  0) 0) |
| [12] |
易丹辉. 数据分析与EViews应用[M]. 北京: 中国人民大学出版社, 2014 (Yi Danhui. Data Analysis and EViews Application[M]. Beijing: China Renmin University Press, 2014)
(  0) 0) |
| [13] |
张良均, 杨坦, 肖刚, 等. MATLAB数据分析与挖掘实战[M]. 北京: 机械工业出版社, 2015 (Zhang Liangjun, Yang Tan, Xiao Gang, et al. MATLAB Data Analysis and Data Mining[M]. Beijing: China Machine Press, 2015)
(  0) 0) |
| [14] |
王正林, 龚纯, 何倩. 精通MATLAB科学计算[M]. 北京: 电子工业出版社, 2012 (Wang Zhenglin, Gong Chun, He Qian. Proficient in MATLAB Scientific Computing[M]. Beijing: Electronic Industry Press, 2012)
(  0) 0) |
 2017, Vol. 37
2017, Vol. 37