2. 枣庄市薛城区交通运输局, 枣庄市黄河中路, 277000;
3. 65631部队, 锦州市, 121000
随着MEMS制造技术和工艺的发展, MEMS陀螺的性能得到了显著的提高, 但因MEMS陀螺中所固有的白噪声、闪烁噪声等, 使其精度无法胜任长时间导航[1], 因此, 选择合适的算法去除随机误差显得尤为重要。近年来, 小波变换因其良好的时频分析特性和多分辨率能力在工程实践中得到了广泛应用, 但小波滤波需要人为设定分解层次与小波基, 且分解结果受信号特性影响较大[2]。经验模态分解(empirical mode decomposition, EMD)方法是一种数据驱动的自适应时域分析方法, 其可以根据信号自身特点将信号按照频率和幅值逐级分解成本征模态函数(intrinsic mode function, IMF)[3]。由于EMD方法不需要信号的先验信息, 也不存在信号变换域分析的误差, 因而广泛应用于非线性信号的消噪应用中[4]。
互补集合经验模态分解CEEMD(complementary ensemble empirical mode decomposition)是基于EMD和总体经验模式分解(EEMD)提出的一种改进算法, 该方法不但可解决EMD方法的模态混叠和能量泄露问题, 且避免了加入白噪声后EEMD的分解误差。EMD滤波及其改进滤波分为强制消噪算法和阈值滤波消噪算法, 其中强制消噪算法利用分解得到的IMF直接部分重构消噪信号, 容易丢失信号中含有的有用信息, 继而导致信号变形[5]。崔冰波等[6]在周期图法标示光纤陀螺随机误差特征参数的基础上, 利用本征模态函数筛选的阈值滤波算法对光纤陀螺的随机误差进行了消噪处理, 结果表明, 其对光纤陀螺随机噪声有较好的抑制作用。
考虑到MEMS陀螺与光纤陀螺的随机误差存在较大差别, 为运用合适算法处理MEMS陀螺的随机误差, 本文在由本征模态函数样本熵和相似度参数线性组合确定复合指标的基础上, 提出基于复合指标筛选本征模态函数的互补集合经验模态分解阈值滤波降噪算法。最后, 利用仿真数据和实例数据证明了该算法的有效性, 且该算法在消噪效果、适应性方面都有较大的提高。
1 CEEMD阈值滤波 1.1 CEEMD原理CEEMD为避免EMD分解的模态混叠现象, 将正负高斯白噪声加入到待处理信号中, 利用高斯白噪声具有频率平均的特点, 消除了待处理信号在时间尺度上的间歇性。根据零均值高斯白噪声的特性, 经过几次平均处理后, 噪声将会相互抵消[7-9]。
1.2 IMF复合筛选算法CEEMD将含有随机误差噪声的各谐波分量分解成主成分为噪声的IMF、可用信号与噪声混杂的IMF和纯信号IMF。强制消噪滤波是将主成分为噪声的IMF直接删除再重构。阈值消噪根据各IMF特性设定阈值, 剔除各IMF中的噪声, 保留有用信号。但无论强制消噪滤波方法还是阈值滤波都需要将IMF分量进行有效筛选, 以进行下一步运算。
样本熵(sample entropy, SE)[10]是一种区别于近似熵的时间序列自身相似统计量。样本熵对样本数量不敏感, 使用较少的数据就能得到稳定值, 且分析效果较好。文献[11]将IMF分量的概率密度函数(PDF)与原始信号的PDF之间的相似度q作为筛选IMF分量的标准。相似度q定义为:
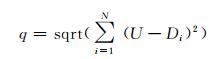
|
(1) |
式中, N为滤波窗口内数据长度, Di为第i个IMF分量的PDF, U为原始信号。本文利用样本熵SE与相似度q的复合指标L筛选IMF。因样本熵和相似度指标的基数不同, 因而不能进行简单的集合。为了将两者合理地规划到同一量级中进行比较, 需要对指标进行归一化处理:
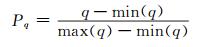
|
(2) |
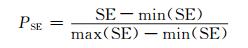
|
(3) |
式中, Pq和PSE分别为标准化处理后的相似度和样本熵, max()和min()分别为取最大值和最小值操作。在指标的组合过程中, 复合评价指标L的线性组合权重经过多次实验验证被设定为0.9和0.1, 故其表达式为:
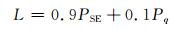
|
(4) |
CEEMD将含有随机误差噪声的各谐波分量分解成主成分为噪声的IMF、可用信号与噪声混杂的IMF和纯信号IMF。CEEMD阈值消噪滤波重点在于阈值的设定, 可将主成分为噪声的IMF、可用信号与噪声混杂的IMF中的噪声剔除, 保留可用信号部分。因在惯性器件消噪过程中软阈值会丢失较多的细节信息, 使信号变形[12], 故本文借鉴小波的硬阈值函数设定各IMF分量阈值为:
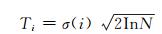
|
(5) |
式中, N为样本个数。假设前k项IMF的主成分为噪声, 第p项IMF为可用信号与噪声混杂的IMF和纯信号IMF的分界, 针对前k项主成分为噪声的IMF的标准差为:
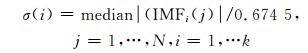
|
(6) |
信号与噪声混杂的IMF的方差V(i)(k < i≤p)模型为[13]:

|
(7) |
式中, ρH≈2.01+0.2(H-0.5), H为随机噪声参数, 则所有的阈值函数:
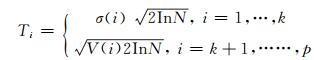
|
(8) |
因此, CEEMD阈值滤波算法的具体过程为:
1) 对信号进行CEEMD分解, 获取IMF分量;
2) 利用复合指标L筛选IMF分量, 确定分界点k和p;
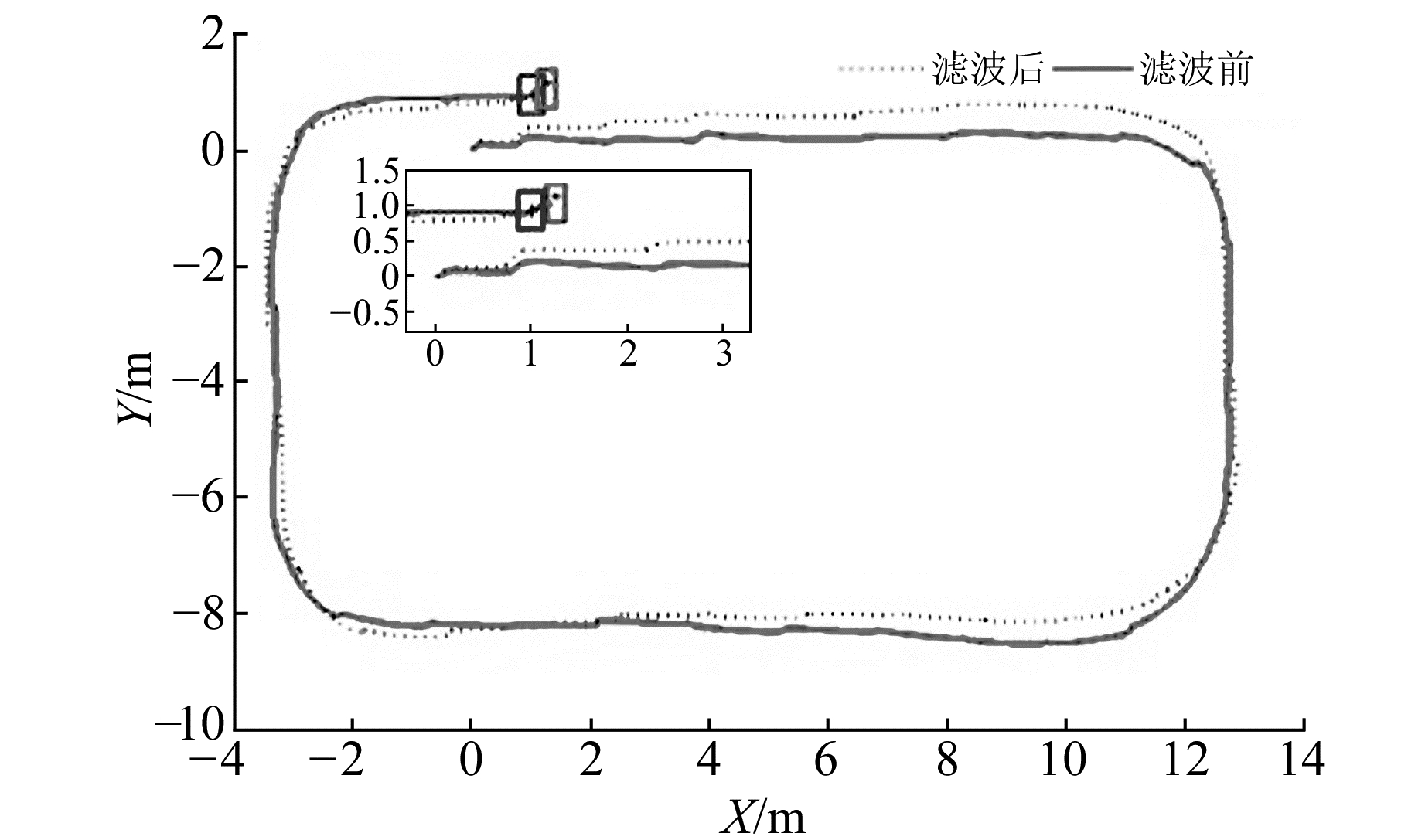
3) 计算各个IMF的阈值函数Ti, 并获取处理后的IMF分量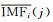
4) 利用处理后的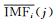
采用仿真算例和MEMS陀螺实测算例验证本文算法的有效性和普适性。
2.1 仿真算例在MATLAB软件中, 标准测试Doppler信号的频率和幅值特性较为接近陀螺信号[14], 因此本文选用Doppler信号进行仿真。为体现本算法的有效性, 在Doppler信号基础上添加H=0.3(σ=0.1, σ=0.3)和H=0.7(σ=0.1, σ=0.3)的分形噪声进行分析。
计算各IMF分量的样本熵SE和相似度q, 并通过式(4)得到复合指标L, 结果如图 1所示。

|
图 1 IMF复合指标L Fig. 1 IMF's composite evaluation |
通过图 1可以确定H=0.3(σ=0.1, σ=0.3)和H=0.7(σ=0.1, σ=0.3)信号的IMF分量的分界点k和p。其中H=0.7(σ=0.3)时取k=1、p=7, 其余信号均为k=1、p=9, 并利用式(8)处理得到消噪后的信号, 具体对比如图 2所示。
|
图 2 CEEMD阈值消噪效果对比 Fig. 2 Filtering results of CEEMD threshold de-noising methods |
由仿真结果分析可知(表 1), 基于部分IMF分量重构法的强制消噪滤波能够降低信号中分形噪声的影响, 但因其舍弃了噪声与信号混杂的IMF分量致使消噪效果有限、适应性差、噪声滤除效果不稳定。本文的阈值消噪滤波因其较好地保留了各IMF分量中的有用信息, 消噪效果显著, 能滤除80%左右的噪声, 且稳定性较强制消噪滤波有所提高。
|
|
表 1 滤波消噪前后信号RMSE误差 Tab. 1 RMSE errors of signal before and after filtering |
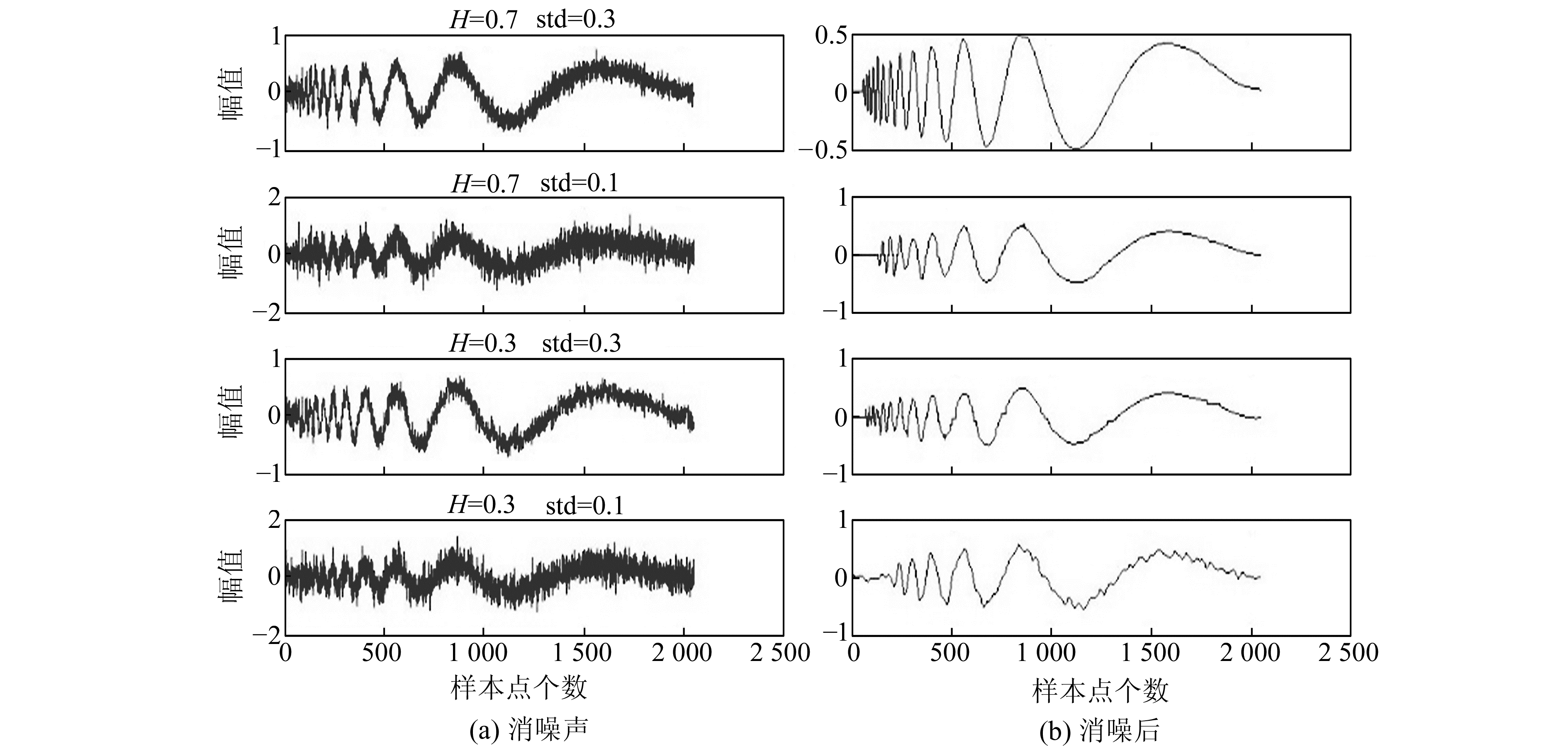
以100 Hz的频率在静态条件下采集70 s的MEMS陀螺数据进行实例验证, 使用低通滤波器让数据变得较为稳定, 其中该款陀螺的随机噪声参数H=0.647 4。根据上文介绍, 首先使用CEEMD分解得到13个IMF分量; 然后通过样本熵SE和概率密度相似度q获取各IMF分量的复合指标L, 确定k=1、p=9;最后对筛选后的各IMF分量进行阈值消噪处理, 得到重构结果。MEMS陀螺的初始信号和滤波消噪后的信号如图 3所示。
|
图 3 滤波前后MEMS陀螺信号 Fig. 3 MEMS-gyro signal before and after filtering |
从图 3可以看出, CEEMD阈值滤波后, MEMS陀螺数据中的噪声大幅降低。为了定量验证本文方法的有效性, 选取均方根误差(RMSE)和Allan方差提取零偏不稳定性和速率斜坡来分析滤波效果。
由表 2可见, 通过低通滤波器后的MEMS陀螺信号各项误差参数相对较小, 且经过本文阈值滤波算法后的各项误差参数进一步下降, 具体表现为零偏不稳定性下降了76.4%, 速率斜坡下降了62.3%, 均方根误差下降了67.5%。
|
|
表 2 MEMS陀螺滤波前后参数 Tab. 2 Noise parameters of MEMS-gyro before and after filtering |
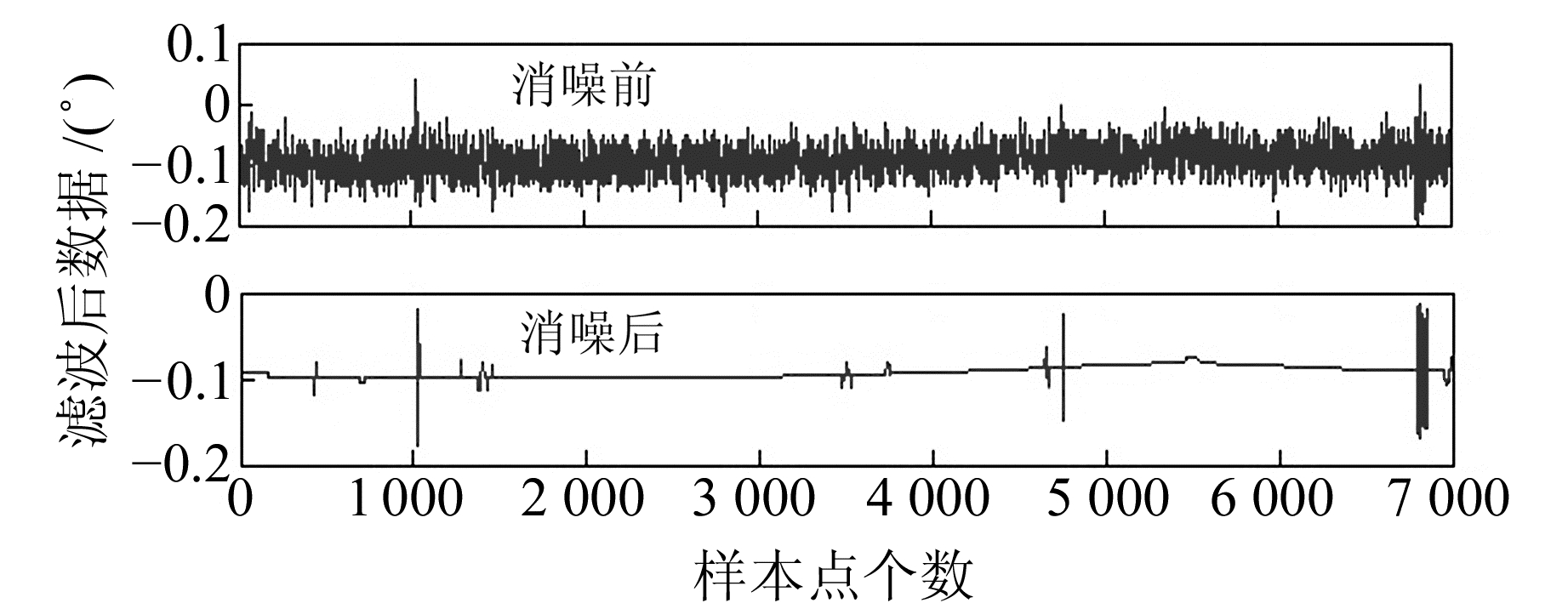
针对CEEMD分解的阈值消噪滤波算法在动态数据中的表现, 本文采用一组行人导航MEMS-IMU数据验证算法的有效性。捆绑有MEMS-IMU的行人在房间内走一个闭合的矩形, 行人开始的位置设定为(0, 0), 以惯性数据推导得到的结束位置同初始位置的偏差作为评价指标。具体的陀螺处理过程同上, 滤波前后行人的运动轨迹见图 4, 具体数据见表 3。
|
图 4 滤波前后轨迹 Fig. 4 Trajectory before and after filtering |
|
|
表 3 行人位置偏差 Tab. 3 Position deviation for pedestrian |
本文在确定MEMS陀螺噪声特征参数的基础上, 提出基于复合指标筛选本征模态函数的互补集合经验模态分解的阈值滤波降噪算法。该算法首先运用CEEMD将信号分解为IMF分量, 再以样本熵和概率密度相似度的复合指标对IMF分量进行筛选, 最后根据各IMF特性采用阈值滤波对噪声信号进行滤除。仿真和MEMS陀螺实例数据分析表明, 基于CEEMD阈值滤波算法较传统的部分重构强制消噪滤波算法在适应性、噪声剔除效果方面具有一定的优势, 能够滤除绝大部分的噪声。具体表现为静态条件下零偏不稳定性下降了76.4%, 速率斜坡下降了62.3%, 均方根误差下降了67.5%;在行人导航应用中的轨迹闭合差X方向降低了24.6%, Y方向降低了10.6%。
| [1] |
Fang B, Chou W S, Ding L. An Optimal Calibration Method for a MEMS Inertial Measurement Unit[J]. International Journal of Advanced Robotic Systems, 2014, 11(1): 314-319
(  0) 0) |
| [2] |
Ge L, Chen H Y, Han S, et al. Adaptive Filtering of Continuous GPS Results[J]. Journal of Geodesy, 2000, 74(7-8): 572-580 DOI:10.1007/s001900000120
(  0) 0) |
| [3] |
甘雨, 隋立芬. 基于经验模分解的陀螺信号消噪[J]. 测绘学报, 2011, 40(6): 745-750 (Gan Yu, Sui Lifen. De-Noising Method for Gyro Signal Based on EMD[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 745-750)
(  0) 0) |
| [4] |
崔冰波, 陈熙源. 基于一种改进EMD算法的GPS多径效应抑制方法[J]. 中国惯性技术学报, 2014, 22(3): 346-351 (Cui Bingbo, Chen Xiyuan. Multipath Mitigation of GPS Signal Based on Improved EMD Algorithm[J]. Journal of Chinese Inertial Technology, 2014, 22(3): 346-351)
(  0) 0) |
| [5] |
张文忠, 周荣, 武旭红, 等. 利用白噪声分解特征的EEMD阈值降噪方法[J]. 测绘科学技术学报, 2013, 30(5): 255-259 (Zhang Wenzhong, Zhou Rong, Wu Xuhong, et al. A Threshold De-Noising Method Based on the Characteristics of White Noise Decomposed by EEMD[J]. Journal of Geomatics Science and Technology, 2013, 30(5): 255-259)
(  0) 0) |
| [6] |
崔冰波, 陈熙源, 龚政仰. 基于经验模态概率分布的光纤陀螺信号处理[J]. 中国惯性技术学报, 2015, 23(5): 690-695 (Cui Bingbo, Chen Xiyuan, Gong Zhengyang. Fiber Optic Gyro Signal Processing Based on Empirical Mode Probability Distribution[J]. Journal of Chinese Inertial Technology, 2015, 23(5): 690-695)
(  0) 0) |
| [7] |
Li M, Li F C, Jing B B, et al. Multi-Fault Diagnosis of Rotor System Based on Differential-Based Empirical Mode Decomposition[J]. Journal of Vibration and Control, 2015, 21(9): 1 821-1 837 DOI:10.1177/1077546313502505
(  0) 0) |
| [8] |
甘雨, 隋立芬, 王冰. 经验模态分解阈值消噪方法及其在惯性导航系统数据处理中的应用[J]. 测绘学报, 2012, 41(4): 504-509 (Gan Yu, Sui Lifen, Wang Bing. EMD Threshold De-Noising and Its Applications in INS Data Processing[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 504-509)
(  0) 0) |
| [9] |
Yeh J R, Shieh J S, Huang N E. Complementary Ensemble Empirical Mode Decomposition:A Novel Noise Enhanced Data Analysis Method[J]. Advances in Adaptive Data Analysis, 2010, 2(2): 135-156 DOI:10.1142/S1793536910000422
(  0) 0) |
| [10] |
Richman J S, Moorman J R. Physiological Time-Series Analysis Using Approximate Entropy and Sample Entropy[J]. American Journal of Physiology:Heart and Circulatory Physiology, 2000, 278(6): 2 039-2 049 DOI:10.1152/ajpheart.2000.278.6.H2039
(  0) 0) |
| [11] |
Komaty A, Boudraa A O, Augier B, et al. EMD-Based Filtering Using Similarity Measure between Probability Density Functions of IMFs[J]. IEEE Transactions on Instrumentation and Measurement, 2014, 63(1): 27-34 DOI:10.1109/TIM.2013.2275243
(  0) 0) |
| [12] |
Wang Y H, Yeh C H, Young H W V, et al. On the Computational Complexity of the Empirical Mode Decomposition Algorithm[J]. Physica A:Statistical Mechanics and Its Applications, 2014, 400: 159-167 DOI:10.1016/j.physa.2014.01.020
(  0) 0) |
| [13] |
Gan Y, Sui L F, Wu J F, et al. An EMD Threshold De-Noising Method for Inertial Sensors[J]. Measurement, 2014, 49: 34-41 DOI:10.1016/j.measurement.2013.11.030
(  0) 0) |
| [14] |
肖文健, 陈志斌, 马东玺, 等. 光纤陀螺基于本征模态函数筛选的阈值滤波算法[J]. 中国惯性技术学报, 2015, 23(5): 685-689 (Xiao Wenjian, Chen Zhibin, Ma Dongxi. De-Noising Method of FOG with DEMD Threshold Based on IMF Criterion[J]. Journal of Chinese Inertial Technology, 2015, 23(5): 685-689)
(  0) 0) |
2. Xuecheng Transport Bureau, Middle-Huanghe Road, Zaozhuang 277000, China;
3. PLA 65631 Troops, Jinzhou 121000, China
 2017, Vol. 37
2017, Vol. 37




