2. 江苏省资源环境信息工程重点实验室, 徐州市大学路1号, 221116
水汽层析技术具有高时空分辨率、精度好、成本低、全天候的优点[1-3]。GPS信号穿过对流层时会产生路径延迟(slant total delay, STD), 而其中包含的路径湿延迟(slant wet delay, SWD)同水汽参数之间具有很好的相关性, 从而可以通过求解层析方程组获得水汽参数。最早的求解方法是文献[1]提出的奇异值分解法SVD(同时加入水平、垂直、边界约束条件), 但SVD无法解决由于信号噪声、测站分布不均、信号量少等因素引起的水汽场重构的质量问题。为此, 有学者提出了Kalman滤波的方法, 该方法减弱了对先验信息的依赖, 但很大程度上仍会受到GPS几何网形和信号噪声的影响。本文介绍的ART(algebraic reconstruction technique)算法最早应用于GPS电离层层析[4-5], 之后Bender等[6-7]和王维等[8]提出利用其进行水汽层析方程组的解算, 该算法抗噪性强, 即使GPS信号观测量较少, 信号分布不均, 观测值噪声较大, 仍可获得精度较高的解算结果[9]。
本文介绍了GPS水汽层析技术的基本原理以及层析方程组的组成, 通过对影响ART方法收敛速度和精度的松弛因子、投影次序、停止规则、非负特性进行讨论, 结合水汽层析问题的特点, 提出一种基于分组排序的水汽层析约束ART算法。实验由香港卫星定位参考站网(SatRef)提供GPS信号数据, 实验结果与传统的ART算法相比表明, 本文算法提高了收敛速度以及层析结果的精度。
1 GPS层析原理 1.1 观测方程信号传播路径上的水汽总含量称为SWV(slant water vapor), 其包含了对流层垂直方向的水汽信息, 可以表示为[10]:
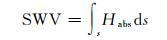
|
(1) |
式中, Habs为绝对湿度(水汽参数), s为信号路径。通常采用直线路径代替其实际路径[14]。将上述积分方程离散化为:
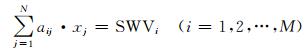
|
(2) |
式中, aij为第i条信号穿过第j个体素的截距长度, 若无信号穿过, 则对应的截距长度为0, xj对应层析区域的第j个体素的水汽参数, SWVi为第i条信号的SWV观测值。式(2)也可用矩阵形式表示为Aobsx = bobs, 其中, Aobs为系数矩阵, 由aijk组成, bobs由观测值SWVi组成, x即是所要求的水汽参数值。
1.2 层析方程观测方程组和约束方程的组合即为求解水汽参数的层析方程组:
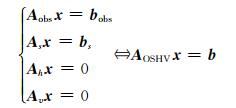
|
(3) |
式中, Aobs、As、Ah、Av分别为观测、地表约束、水平约束、垂直约束方程组的系数矩阵, bobs为SWV的观测值, bs为地面测站位置的水汽参数观测值。
由于水汽密度随高度增加而呈现指数递减的特性, 水汽含量在高层很少, 所以很多学者都采用水汽场顶层水汽密度约束为0或者约束为一极小数值的边界约束条件, 该条件可视作一种先验信息。但该约束条件过于强制, 并不适合所有情况下的水汽层析, 因此实验并未采用。考虑到水汽参数具有非负特性, 本文提出在每次迭代的过程中增加水汽参数非负约束, 保证了其非负的特性, 并获得了顶层的水汽层析结果。为方便讨论, 对各类方程组用大写字母进行分类:O表示观测方程组、S表示地表约束方程组、H表示水平约束方程组、V表示垂直约束方程组, 则式(3)的排序可表示为OSHV。
2 ART算法 2.1 ART算法原理设方程组(3)的系数矩阵为M行N列, 则每一个方程都表示一个N维空间内的超平面, 而要求解的水汽参数x是N维空间中一个点的位置。当方程组存在唯一解时, 该解是M个超平面的交点。ART算法的基本思想是从给定的初始解出发, 将该点按某种顺序依次投影到相关的超平面上, 通过反复的投影, 到达这M个超平面的交点位置。ART算法的步骤是先假设一初始水汽参数x0(可取数值为0的向量), 通过式(4)求取一次近似解xk+1, 再根据xk+1求二次近似解xk+2, 直到满足迭代的条件结束:
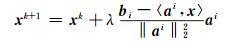
|
(4) |
式中, bi为方程组第i行方程右侧数值, ai为第i行方程的系数向量, λ为松弛因子。
2.2 松弛因子当观测值无误差时, 使用ART方法直接将初值投影到超平面进行计算即可获得最终解。但是由于观测值中存在噪声(误差), 所以需要加入松弛因子, 修正每次迭代中近似解投影到下一个超平面的位置, 减小水汽层析方程组解算的误差。本文通过实验来选择最优的松弛因子[9]。
2.3 投影次序投影次序是指使用ART算法时迭代方程的排序。投影次序的不同会直接影响迭代的速度以及解的精度[11]。根据文献[12]对CT图像重建的ART算法投影排序的描述, 本文提出了水汽层析的投影排序去相关原则:被用于迭代的观测方程的序列, 其观测值SWVi应尽可能均匀分布, 不能出现聚类现象。由于SWV的大小同信号的高度角以及方位角密切相关, 因此按照上述投影原则, 可以尽量减少方程之间的相关性, 避免最终解偏向某一类观测值提供的信息。基于该原则进行迭代计算时, 更容易获取全局信息, 从而提高收敛速度。
2.4 停止规则由于层析方程是过约束的, 并且观测值存在噪声, 所以即使M>N, 也不存在唯一的解, 利用ART迭代获得的解并不收敛于超平面上的一个点, 而是在层析方程中各个方程所代表的超平面相交的区域来回摆动。本文采用文献[7]中的停止规则判定迭代停止。
3 基于分组排序的水汽层析约束的ART算法通过研究影响层析方程组解算因素, 本文提出基于分组排序的水汽层析约束ART算法。该方法通过对层析方程组按照(伪)观测值精度进行分组, 使最终解偏向精度较高的数据[11]。由于观测方程组精度最高, 因此排在第1组; 垂直约束条件通过探空数据获取, 精度较高, 分为第2组; 地面约束条件是通过气象数据获取的真实数据, 但却无法表示所在体素块的平均水汽含量, 分为第3组; 由于水平约束本身就是为了获取未知体素内水汽参数才加入的约束, 精度最低, 分为第4组。则按前文规定, 最优分组为OVSH。
分组完成后, 对第1组观测方程按照水汽层析的投影排序原则进行排序。首先将所有SWV观测值从小到大进行排序, 然后平均分成4组, 每次从4组中抽取中间值排序, 直到完成所有观测方程的排序。该方法保证了解在偏向可靠信息的情况下的“无偏性”。
由于水汽层析解的非负特性, 在分组排序完成后, 需要加入非负约束。式(5)为该约束的映射方法, 如式(6)所示, 对每次计算的迭代解加入非负映射。后续使用括号作为增加非负约束的符号, 如(OVSH)表示加入非负约束的层析方程组OVSH。
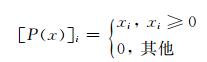
|
(5) |
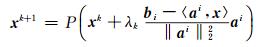
|
(6) |
实验采用香港9个参考站的GPS数据, 图 1是参考站在层析网格中的位置分布图, 三角形表示参考站, 圆形表示气象站。层析区域范围为东经113.841°~114.425°、北纬22.078°~22.618°, 层析最高层为10 km。研究区域沿东西及天顶方向划分为4×4×10共160个体素。实验时间跨度为2014-03-25~03-30 (年积日84~89), 采样开始时间为UTC 0时, 采样持续时间30 min, 层析采样间隔5 min。

|
图 1 测站位置分布 Fig. 1 Distribution of the sites inside the tomography grid |
获取的GPS数据通过GAMIT软件进行解算, 具体处理方案见表 1。采用HKKP的数据作为评价解算结果的标准。水汽参数初值设为0, 可以体现改进算法在收敛速度上的优势。
|
|
表 1 GAMIT处理方案 Tab. 1 GAMIT processing scheme |
根据前文的方法, 将HKKP气象站数据作为真值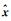
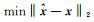
|
|
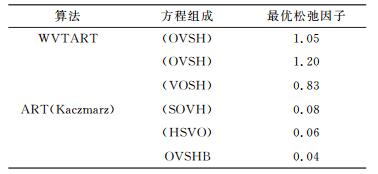
表 2 各种方案的最优松弛因子 Tab. 2 The optimal relaxation parameter for schemes |
通过分析(OVSH)、(VOSH)、(SOVH)、(HSVO)4种不同分组的迭代次数和精度, 证明了最优分组方法的合理性。图 2是2014-03-25(年积日84)各分组的RMSE曲线图, 横轴表示迭代次数, 纵轴表示RMSE。从图中可以看出, 精度从高到低分组的(OVSH)方案精度最高, 且在迭代20次后就达到收敛, 而按照精度从低到高的分组(HSVO)精度最差, 该方案迭代次数最多(238次)。(VOSH)与(SOVH)精度相差不大, 但(VOSH)迭代次数为26次, (SOVH)则为197次。

|
图 2 各组RMSE曲线 Fig. 2 RMSE curve of different schemes |
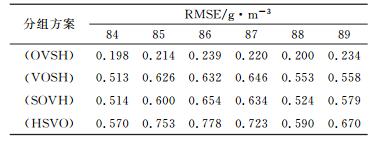
表 3给出了年积日84~89不同分组情况下最优松弛因子迭代解的RMSE。可以看出, 不同分组下的解算结果存在较大差异; (OVSH)分组同其他分组相比具有更高的精度。
|
|
表 3 不同方案的RMSE Tab. 3 RMSE of different schemes |
通过实验证明, 按照方程组精度进行分组可以有效提高ART算法的收敛速度以及最终解的精度。通过双差方法获取的SWV观测值具有很高的精度, 其次是垂直约束方程、地面约束方程, 平面约束方程可信度最低, 且一定程度上影响了方程组解算的精度。
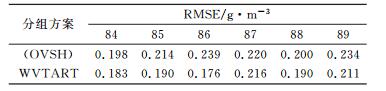
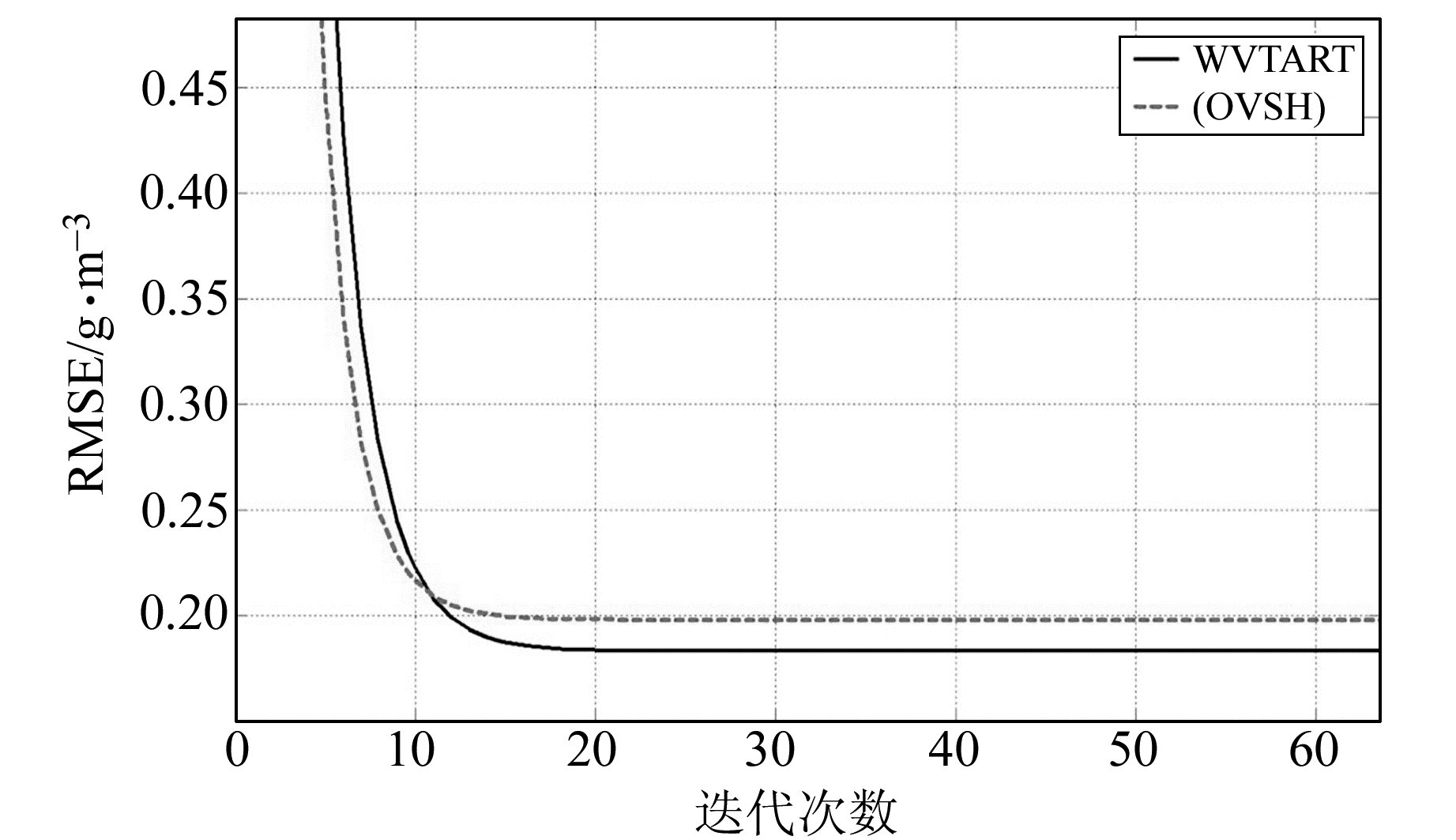
4.2.2 排序对收敛速度和精度的影响通过WVTART算法对最优分组方案(OVSH)按照投影排序去相关原则, 对其观测方程O进行排序, 再利用式(4)进行迭代计算, 最后将最终结果与原方案(OVSH)在收敛速度和精度上进行分析讨论。图 3是2014-03-25(年积日84)两种算法的RMSE曲线图。可以看出, (OVSH)方案经过排序后, 精度提高到0.183 g·m-3。表 4给出了年积日84~89 (OVSH)与WVTART对应的RMSE值, 多天解算结果同样表明WVTART提高了结果精度。
|
图 3 (OVSH) 方案与WVTART算法RMSE曲线 Fig. 3 RMSE curve of (OVSH) scheme and WVTART |
|
|
表 4 (OVSH) 方案与WVTART方案的RMSE Tab. 4 RMSE of (OVSH) scheme and WVTART |
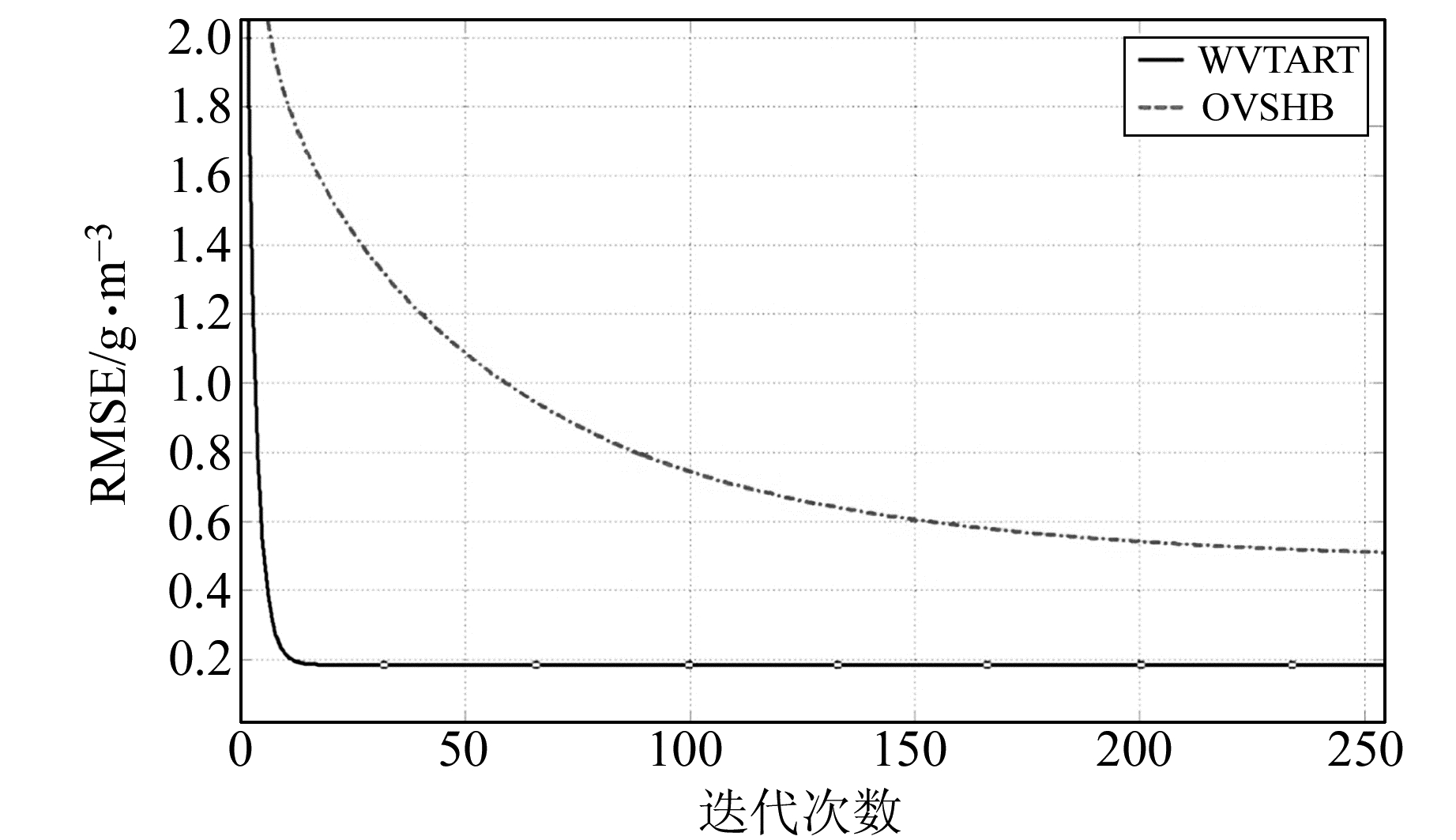
将WVTART算法与使用边界约束条件的OVSHB进行对比。图 4是2014-03-25(年积日84)RMSE曲线图。可以看出, WVTART精度(0.183 g·m-3)要高于使用边界约束条件的OVSHB方程组解算结果(0.482 g·m-3), 而且OVSHB需要迭代416次才能收敛, 在迭代次数上远高于WVTART(19次收敛)。结合表 5中多天两种方案RMSE值对比, 证明了非负约束对方程组解算的收敛速度与精度有很大的影响。图 5是层析区域顶层的水汽等值线分布图。可以看出, 非负约束不仅大大提高了收敛速度和精度, 同时也使层析的顶层获得了水汽信息。
|
图 4 OVSHB方案与WVTART算法RMSE曲线图 Fig. 4 RMSE curve of OVSHB scheme and WVTART |
|
|
表 5 OVSH方案与WVTART方案的RMSE Tab. 5 RMSE of WVTART scheme and OVSHB |
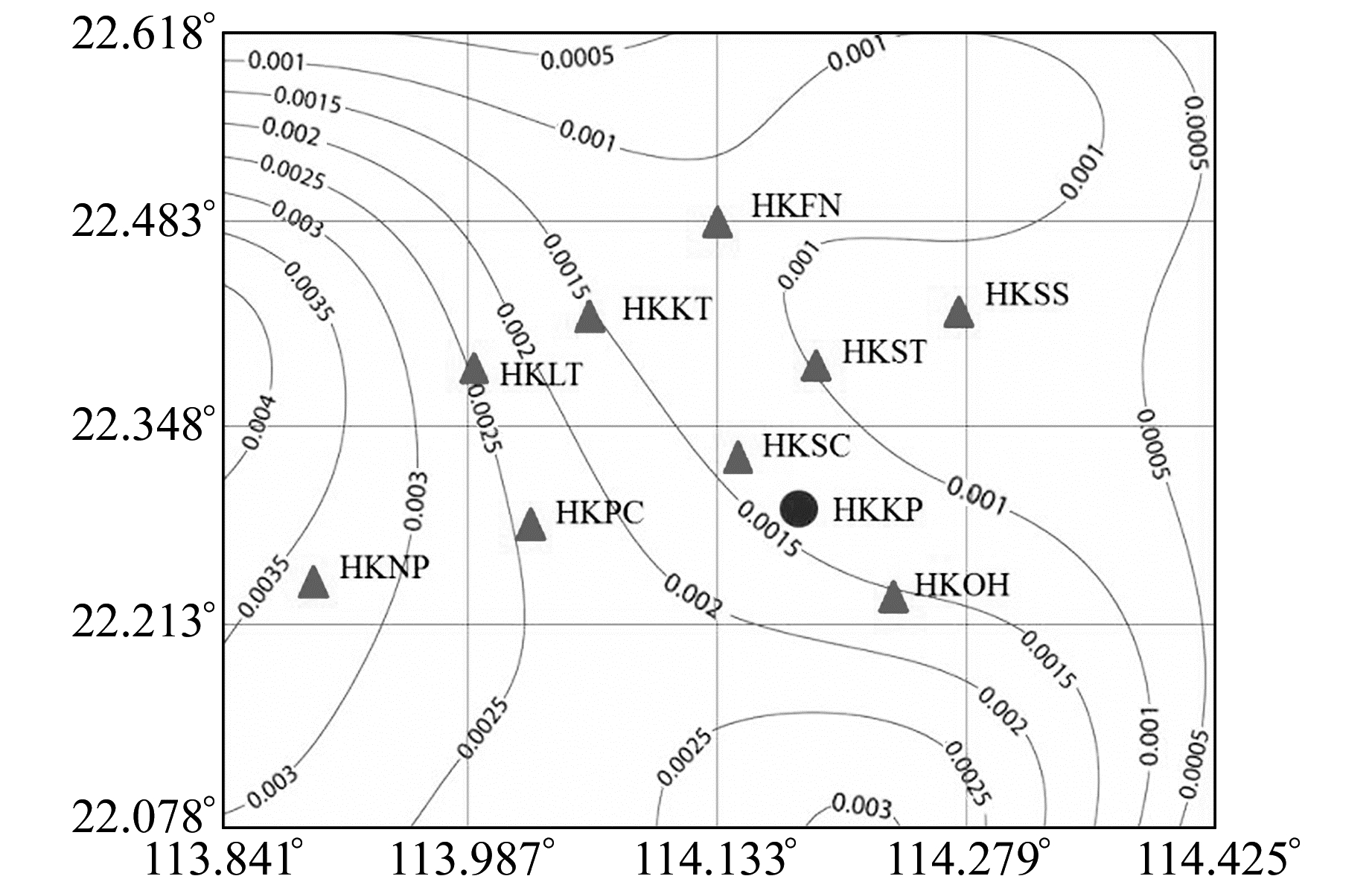
|
图 5 顶层(10 km)水汽等值线图 Fig. 5 Contour of GPS water vapor in the upper boundary layer |
图 6表示2014-03-25~03-30(年积日84~89)UTC 0时WVTART水汽反演结果拟合的水汽廓线与探空数据(RS)对比。可以看出, WVTART拟合的平均水汽廓线与真实水汽数据具有良好的一致性, 而由于水汽层析获取的是水汽在对应层的平均值, 因此当水汽出现不符合水汽分布规律的波动时, 限于其空间分辨率无法感知, 只能获取一定高度层的平均水汽含量。

|
图 6 探空数据与WVTART拟合水汽廓线对比 Fig. 6 Comparison of radio soundings (RS) and WVTART |
本文首先讨论了影响ART解算层析方程组的因素, 如松弛因子、投影次序、非负特性、停止规则, 然后针对水汽层析方程组的特点, 提出了一种基于分组排序的水汽层析约束ART算法(WVTART)以及投影排序的基本原则。
从实验中可以看出, 针对不同类型的层析方程组(观测、垂直约束、地面约束、水平约束方程组)进行分组, 可以有效提高方程解的精度和方程迭代的收敛速度。将层析方程组进行分组, 按照本文提出的水汽层析的去相关原则对观测方程进行排序后, 可进一步提高精度。非负约束是符合水汽参数非负特性的, 弥补了水汽层析区域顶层水汽信息的空白, 约束的加入也同样有效提高了层析方程组的收敛速度与精度。
| [1] |
Flores A, Ruffini G, Rius A. 4D Tropospheric Tomography Using GPS Slant Wet Delays[J]. Annales Geophysicae-Atmospheres Hydrospheres and Space Sciences, 2000, 18(2): 223-234
(  0) 0) |
| [2] |
Hirahara K. Local GPS Tropospheric Tomography[J]. Earth Planets and Space, 2000, 52(11): 935-939 DOI:10.1186/BF03352308
(  0) 0) |
| [3] |
Seko H, Shimada S, Nakamura H, et al. Three-Dimensional Distribution of Water Vapor Estimated from Tropospheric Delay of GPS Data in a Mesoscale Precipitation System of the Baiu Front[J]. Earth Planets and Space, 2000, 52(11): 927-933 DOI:10.1186/BF03352307
(  0) 0) |
| [4] |
Stolle C, Schlüter S, Heise S, et al. A GPS Based Three-Dimensional Ionospheric Imaging Tool:Process and Assessment[J]. Advances in Space Research, 2006, 38(11): 2 313-2 317 DOI:10.1016/j.asr.2006.05.016
(  0) 0) |
| [5] |
Zhai Y, Cummer S A. A Flexible and Robust Direct Reconstruction Method for Magnetospheric Radio Tomography[J]. Radio Science, 2005, 40(3): 119-134
(  0) 0) |
| [6] |
Bender M, Dick G, Wickert J, et al. Estimates of the Information Provided by GPS Slant Data Observed in Germany Regarding Tomographic Applications[J]. Journal of Geophysical Research:Atmospheres, 2009, 114(D6)
(  0) 0) |
| [7] |
Bender M, Dick G, Ge M, et al. Development of a GNSS Water Vapour Tomography System Using Algebraic Reconstruction Techniques[J]. Advances in Space Research, 2011, 47(10): 1 704-1 720 DOI:10.1016/j.asr.2010.05.034
(  0) 0) |
| [8] |
王维, 王解先. 联合迭代重构算法在对流层水汽三维重构中的应用研究[J]. 大地测量与地球动力学, 2011, 31(6): 100-103 (Wang Wei, Wang Jiexian. Application of Simultaneous Iterations Reconstruction Technique for 3D Water Vapor Tomography System[J]. Journal of Geodesy and Geodynamics, 2011, 31(6): 100-103)
(  0) 0) |
| [9] |
Herman G T, Meyer L B. Algebraic Reconstruction Techniques Can Be Made Computationally Efficient(Positron Emission Tomography Application)[J]. IEEE Transactions on Medical Imaging, 1993, 12(3): 600-609 DOI:10.1109/42.241889
(  0) 0) |
| [10] |
Midla P, Rannat K, Uba P.Some Problems in Water Vapor Tomography[C].Environment, Ecosystems and Development, Tenerife, 2007
(  0) 0) |
| [11] |
丁楠, 张书毕. 地基GPS水汽层析的投影面算法[J]. 测绘学报, 2016, 45(8): 895-903 (Ding Nan, Zhang Shubi. Land-Based GPS Water Vapor Tomography with Projection Plane Algorithm[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(8): 895-903)
(  0) 0) |
| [12] |
Guan H, Gordon R. A Projection Access Order for Speedy Convergence of ART (Algebraic Reconstruction Technique):A Multilevel Scheme for Computed Tomography[J]. Phys Med Biol, 1994, 39(11): 2 005-2 022 DOI:10.1088/0031-9155/39/11/013
(  0) 0) |
2. Key Laboratory of Resources and Environmental Information Engineering of Jiangsu Province, 1 Daxue Road, Xuzhou 221116, China
 2017, Vol. 37
2017, Vol. 37