2. 广西空间信息与测绘重点实验室, 桂林市雁山街319号, 541006
使用地基GPS遥感水汽时, 加权平均温度(Tm)是一个至关重要的参数[1]。国际上常用的是Bevis利用无线电探空数据推出的适合中纬度地区(27°~65°N)的线性回归公式Tm=70.2+0.72Ts。但该公式在各地区的精度相差较大, 如在中国中部地区偏差达到-4~-6 K[2]。为此, 文献[2]和文献[3-4]分别建立了中国地区和全球的Tm回归公式, 文献[5-8]分别建立了区域的Tm回归公式, 但这些公式的使用都需要当地的实测气象数据, 在缺乏气象观测的地区使用受到限制。文献[9]提出了使用测站位置和年积日来获取全球加权平均温度的方法, 但该方法时间分辨率较低, 无法反映Tm在1 d中的变化情况, 难以满足全球地基GPS气象学实时性和高时间分辨率的要求[10]。GGOS Atmosphere通过对ECMWF的资料进行处理, 在全球提供了时间分辨率为6 h、空间分辨率为2.5°×2°的Tm格网数据, 该格网数据具有较高的时空分辨率, 为缺乏高空气象观测资料的地区获得精确Tm提供了方便[11]。文献[12]对GGOS Atmosphere Tm格网数据在全球和中国地区的整体精度进行了验证与分析, 但由于其采用的是大范围且相对稀疏的无线电探空资料、COSMIC掩星资料, GGOS Atmosphere Tm格网数据在特定区域范围内的精度还有待验证。新疆地区地域辽阔, 大气水汽含量在空间上分布极不均匀, 昼夜温差大, 气候环境恶劣。对新疆地区开展GGOS Atmosphere Tm格网数据适用性分析与研究, 对地区GPS气象学的发展以及GGOS Atmosphere Tm格网数据对恶劣气候环境的适应性都具有较强的现实意义。
1 加权平均温度对GPS遥感水汽的影响地基GPS遥感水汽是利用GPS信号穿越大气层时的对流层延迟中的湿延迟(ZWD), 通过PWV=Π×ZWD来计算水汽含量(PWV)。其中, Π是ZWD与PWV之间的转换系数, 可由式(1)计算:
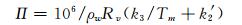
|
(1) |
式中, ρw为水的密度, Rv为水汽气体常数, k′2、k3为大气折射常数。Tm可由式(2)精确计算[10]:

|
(2) |
式中, Pvi为第i层大气的平均水汽压(hPa), Ti为第i层大气的平均温度(K), Δhi为第i层大气的厚度(m)。Pvi、Ti、Δhi可通过测站上空气象资料求取, 但由于大部分GPS站没有装载探空设备, 故难以获得精确的Tm。
由此可见, Π的误差是利用ZWD计算PWV的重要误差来源, 而Tm又是计算Π的关键因子, 因此精确求取Tm对精密遥感水汽含量至关重要; 此外, ZWD的误差也会影响遥感水汽精度。PWV与ZWD、Tm的误差关系可表示为[3]:
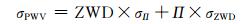
|
(3) |
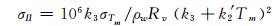
|
(4) |
在缺少气象参数的地区常采用Π=0.15进行气象学研究。假设Π=0.15, 取Tm平均值281 K, 则有:
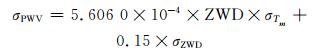
|
(5) |
由文献[3]可知, 通过IGS站提供的ZTD产品和使用气压模型估算的ZHD相减得到的ZWD精度优于1 cm, 而1 cm的ZWD误差引起的PWV误差为1.5 mm。根据气象学的要求, 对PWV的估算精度应达到2.5 ~3.5 mm[13], 因此在不考虑ZWD的估算误差的情况下, 由Tm引起的误差应小于等于1 mm, 才能满足精密遥感水汽含量的需要。
2 新疆地区GGOS Atmosphere加权平均温度的精度分析本文利用探空站所在的GGOS Atmosphere加权平均温度格网, 分别使用平均值法、最近点法、反距离加权法以及双线性插值法, 插值计算探空站位置的Tm。
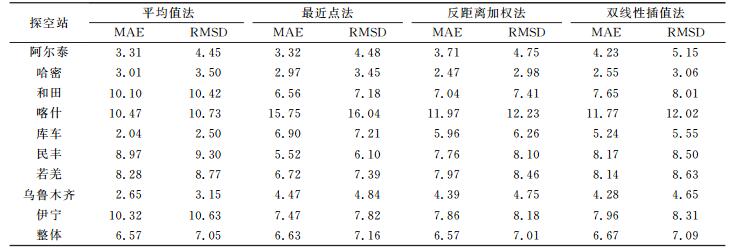
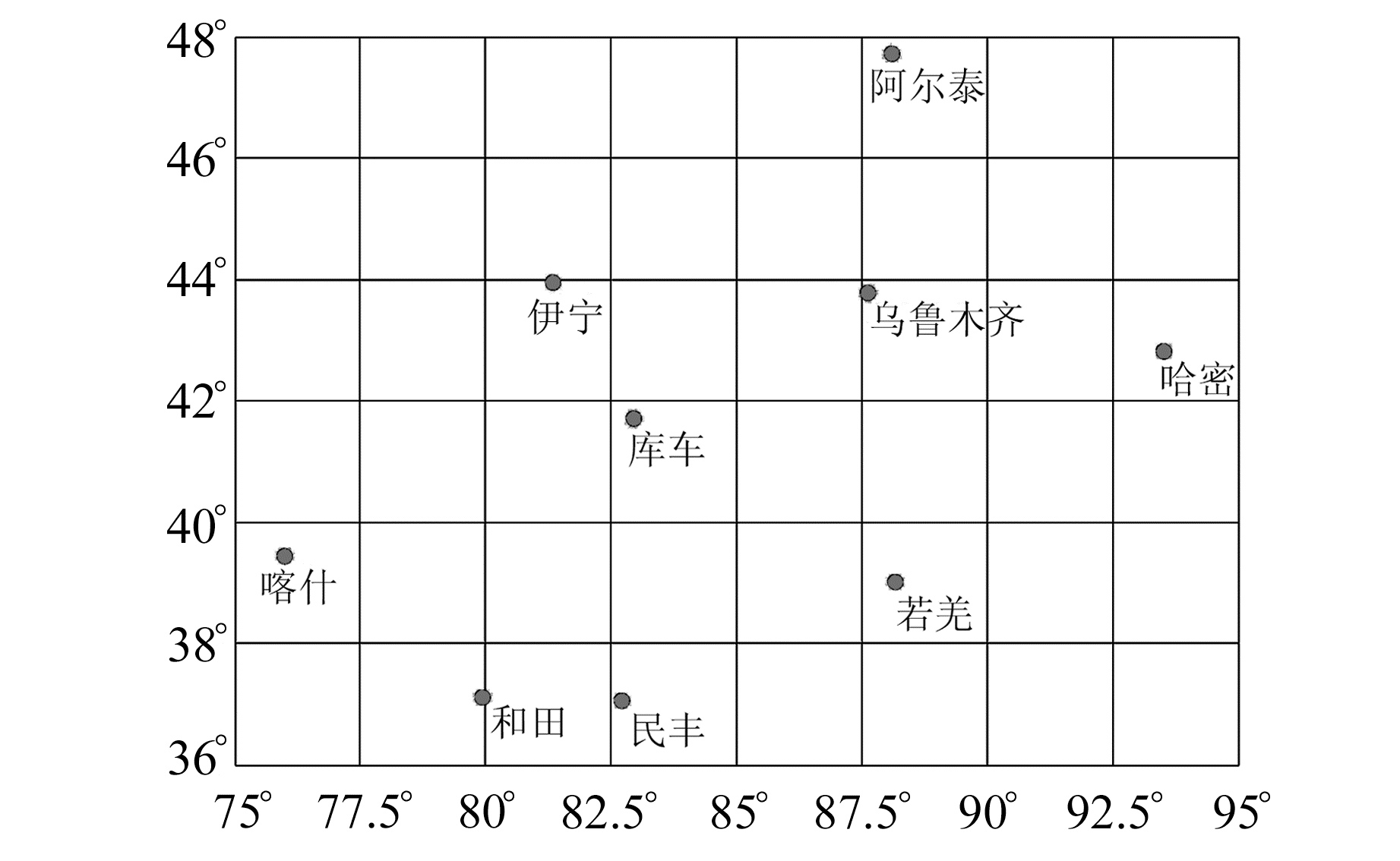
选取新疆地区的9个无线电探空站2013、2014年的数据(地面至3 000 km左右高空17~ 19个等压面分层气象数据, 各层气压约为:地面气压、925 hPa、850 hPa、700 hPa、500 hPa、400 hPa、300 hPa、250 hPa、225 hPa、200 hPa、150 hPa、100 hPa、90 hPa、80 hPa、70 hPa、50 hPa、30 hPa、20 hPa、10 hPa、无。用式(2)计算其每天0时、12时的Tm, 并以此为真值, 对基于GGOS Atmosphere加权平均温度格网数据利用前述4种插值方法计算得到的Tm进行精度检验与分析。为方便描述, 将基于GGOS Atmosphere加权平均温度格网数据利用各种插值方法得到的Tm简称为GTm。新疆地区的9个探空站在GGOS格网中的位置如图 1所示, 9个探空站2013、2014年的GTm精度统计结果(MAE、RMSD)分别见表 1和表 2(单位K)。
|
图 1 新疆地区探空站分布 Fig. 1 Distribution of sounding stations in Xinjiang |
|
|
表 1 2013年GTm年均检验结果 Tab. 1 The annual average precision of GTm in 2013 |
|
|
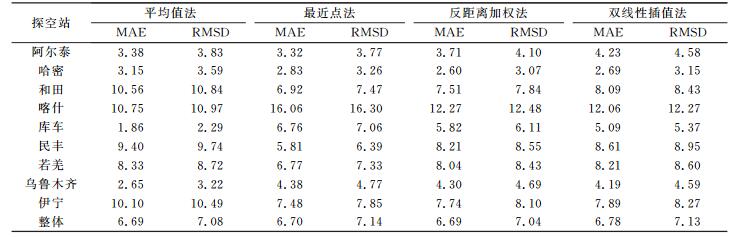
表 2 2014年GTm年均检验结果 Tab. 2 The annual average precision of GTm in 2014 |
结合图 1、表 1和表 2可知, 2 a之间4种方法各自在9个探空站的GTm无论是单站或整体精度都相当, 同一种方法在同一个站的插值精度随年份的变化不大, 说明同一种方法具有相对稳定性。平均值法的GTm在各站2 a之间的MAE、RMSD分布都比较均匀, MAE、RMSD均小于11 K, 且总体的MAE、RMSD均小于最近点法和双线性插值法, 与反距离加权法相比, 其MAE相同, 但RMSD略大; 反距离加权法的MAE、RMSD均小于其他3种方法, 整体精度最高, 但在喀什站出现了12 K左右的MAE和大于12 K的RMSD, 稳定性弱于平均值法; 双线性插值法整体精度最低, MAE、RMSD与平均值法、反距离加权法均相差0.1 K左右。综上可得, 探空站的GTm与格网角点具有相关性, 应用反距离加权法整体上可以获得最高精度的GTm; 平均值法与反距离加权法精度相当(RMSD略大0.04 K, 即使在ZWD达到最大的400 mm时, 引起的PWV误差也不足0.01 mm), 且在各站的精度较反距离加权法分布更均匀、稳定, 没有出现较大的误差。考虑到在一些地区难以获得当地高程来实施反距离加权法, 因此如果要获得较好的GTm, 可优先考虑使用平均值法, 这样既可以保证GTm的精度, 同时计算也更方便快捷。由文献[2]可知, 高精度Tm的RMSD应小于5 K, 因此4种方法都不能保证直接在9个站均获得高精度的GTm; 按文献[12]的方法, 在新疆地区计算Tm的精度也达不到这一要求, 证明在新疆地区研究GTm的精度是必要的, 且GTm可能存在年周期性和区域特性, 有必要对GTm精度的年际变化和空间迁移进行进一步的分析, 以求在新疆地区获得更高精度的GTm。
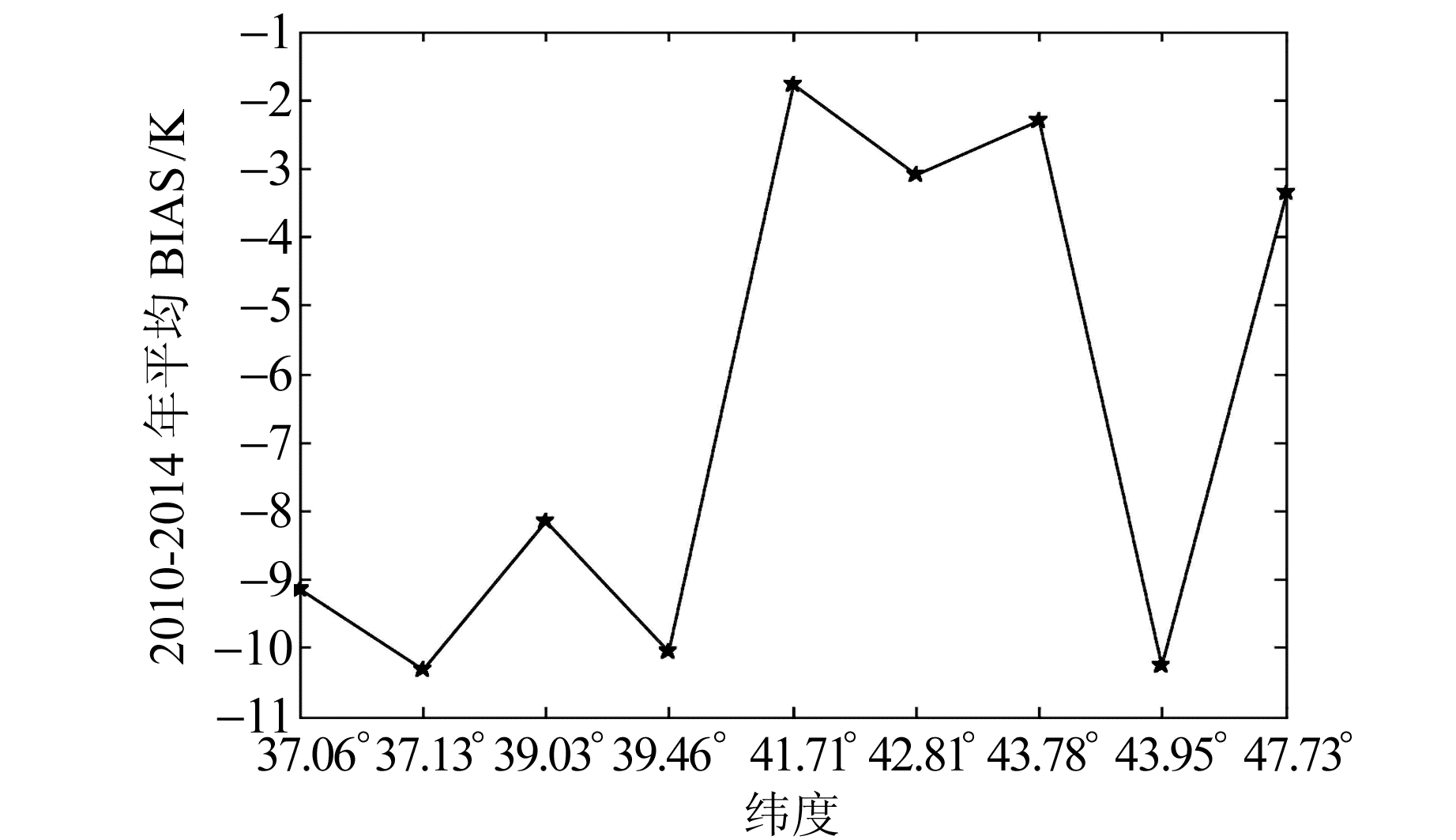
为了获得更高精度的GTm, 本文使用平均值法插值2010~2014年的平均BIAS, 然后进行GTm精度空间迁移的特征分析。GTm随纬度变化的情况见图 2。
|
图 2 年平均BIAS与测站纬度的关系 Fig. 2 Relationship of annual average BIAS and latitude of station |
由图 2可知, 各站的平均BIAS都小于0, 即GTm整体小于真值Tm; 随着纬度的变化, 年平均BIAS被分成了两个部分, 第一部分平均BIAS在[-1.5, -3.5], 第二部分平均BIAS在[-8.0, -10.5]。由此可得, 进行GTm精度变化研究时, 可以将新疆地区分成两个部分, 第一部分为34°~39.46°N以及43.78°~43.95°N, 第二部分为39.46°~43.78°N和43.95°~48.10°N。
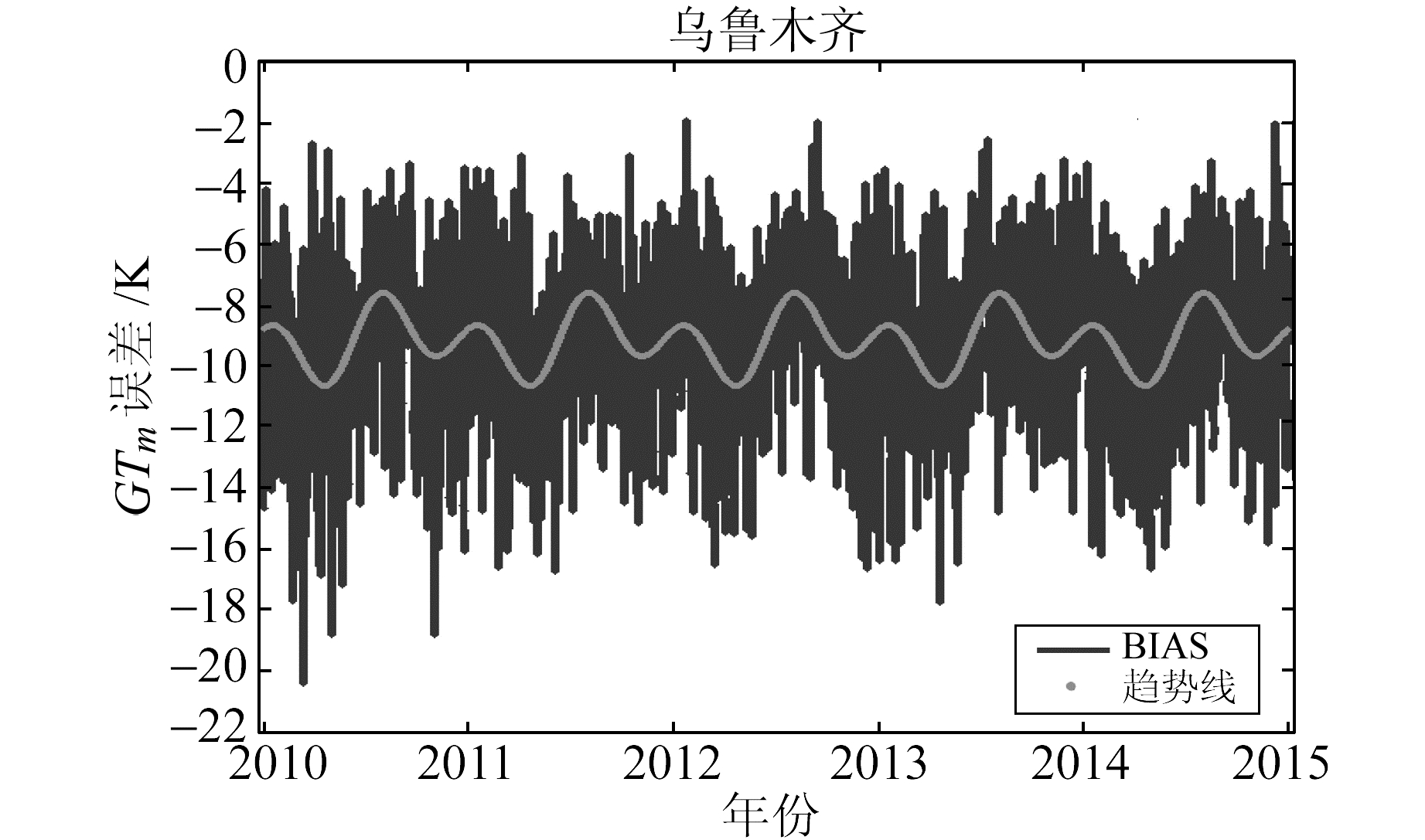
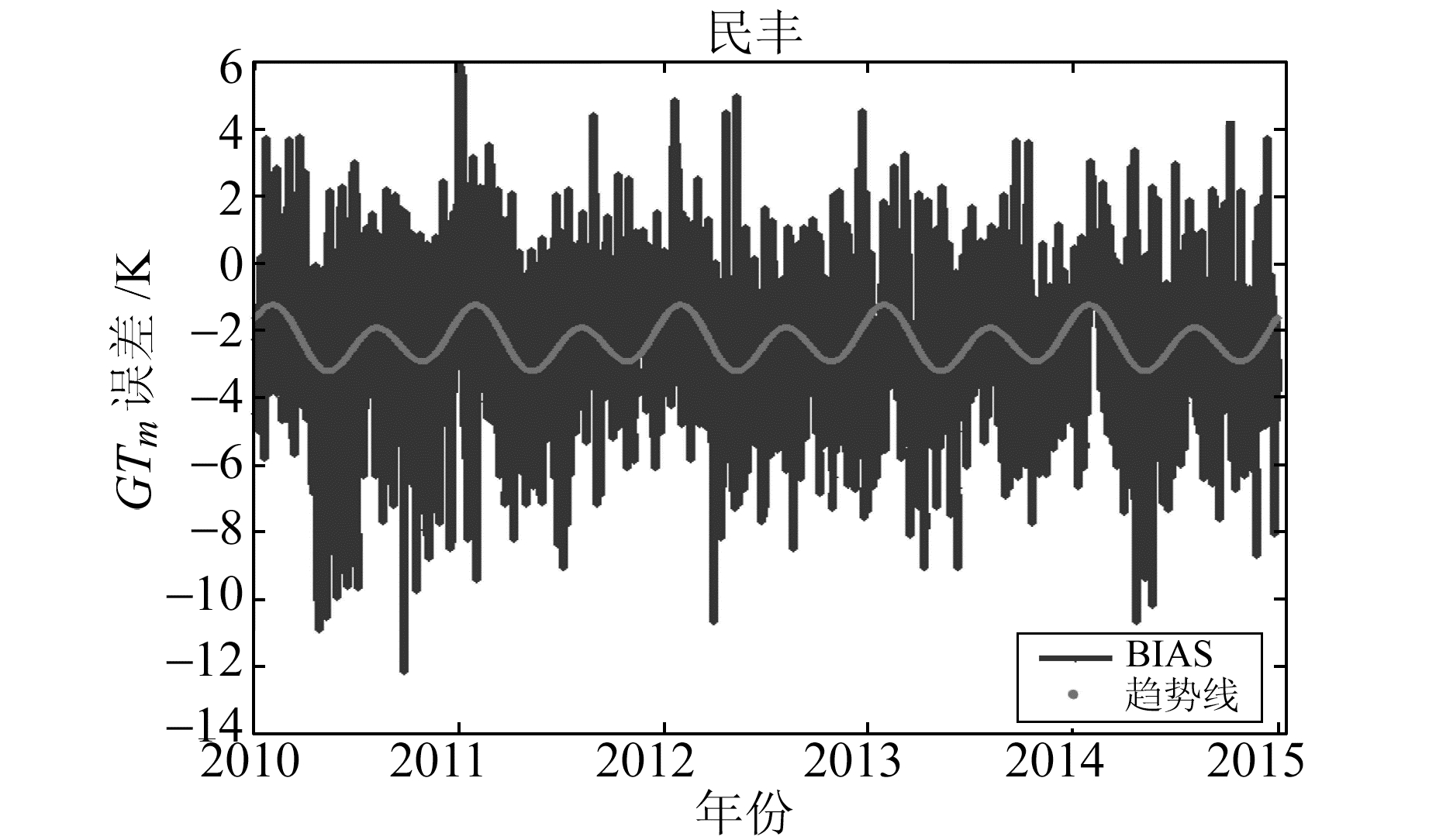
为进一步了解GTm精度的年际变化, 本文分析了2010~2014年平均值法的误差在9个探空站随时间的变化情况。研究发现, 各站GTm的BIAS随着时间的变化表现出一定的年周期和半年周期特性。限于篇幅, 这里只列出2013、2014年乌鲁木齐站、民丰站的BIAS的变化情况(图 3、图 4)。
|
图 3 乌鲁木齐站GTm的BIAS年际变化 Fig. 3 The BIAS annual variation of GTm in Urumqi station |
|
图 4 民丰站GTm的BIAS年际变化 Fig. 4 The BIAS annual variation of GTm in Minfeng station |
通过以上分析可知, 在新疆地区为了获得高精度的GTm, 除了要考虑采用合适的插值计算方法, 还应该考虑GTm的地理位置、年积日。
3 新疆地区GTm的精化 3.1 GTm的精化模型由上节分析结果可知, 按GTm年平均BIAS分布可以将新疆地区分为两个区域, 同时GTm误差呈年周期性和半年周期性。Boehm等[14]使用以1 a为周期的三角函数来拟合全球气温与气压模型(GPT)的气温、气压的季节变化; Lagler等[15]通过估算GPT模型气温、气压的振幅以及年度和半年振幅的相位, 提出了全球气温和气压第二代模型(GPT2);Yao等[3]基于一个带有半年周期和年周期的三角函数, 精化了由其建立的单因素或多因素的全球加权平均温度模型。参考以上方法, 本文拟建立一个考虑地区GTm平均振幅和GTm半年周期、年周期变化的三角函数模型对GTm在新疆地区进行精化改正。
分两个部分求取模型系数, 第一部分为34°~39.46°N以及43.78°~43.95°N, 第二部分为39.46°~43.78°N和43.95°~48.10°N, 精化模型具体形式如下:

|
(6) |
式中, GTmave为平均值法获取的GTm, GTms为经过精化改正后的GTmave, ΔGTm为GTmave与真值Tm的偏差, ΔGTm的表达式为:

|
(7) |
式中, Ai(i=1, 2, 3, 4, 5)为待定系数, doy为对应的年积日。使用2010~2013年9个站的ΔGTm按最小二乘原理解算两个部分的精化模型系数。经解算, 两个部分的ΔGTm具体形式如式(8)、式(9)所示。
第一部分的精化模型:

|
(8) |
第二部分的精化模型:
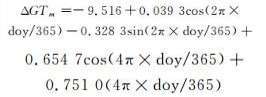
|
(9) |
用精化模型对2010~2013年平均值法计算的9个探空站的GTm进行改正并与探空站真值Tm作差, 以验证模型的内符合精度, 分析模型的可靠性[16]。为方便比较分析, 将2013年各站、整年以及2010~2013年整体统计结果列于表 3(单位K)。
|
|
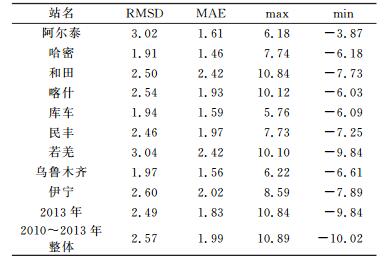
表 3 精化模型的内符合精度 Tab. 3 The precision of inner coincidence of the refined model |
由表 3可以看出, 经过改正后GTm与真值Tm符合较好, 2013年各站的MAE、RMSD都明显减小, GTm的精度显著提高; 所有站的RMSD都在3.04 K以内, MAE小于2.5 K, 2013年整体RMSD减少4 K, 整体MAE下降4.08 K; 和田、喀什、伊宁站的GTm精度提高尤为明显, RMSD从原来的10 K以上下降到不足3 K, MAE从10 K以上减少至2 K左右; 各站的误差最大值绝对值与误差最小值绝对值偏差基本在3 K左右, 误差整体分布比较稳定; 模型整体RMSD、MAE均小于3 K。综上可知, 该精化模型能很好地提高平均值法计算的GTm在新疆地区的精度, 误差分布均匀, 内符合精度较高, 具有很好的可靠性和稳定性。
应用2010~2013年的数据验证精化模型的精度只能分析精化模型的可靠性, 模型在其他年份的适用性及泛化能力还有待验证。为此, 使用精化模型对2014年平均值法计算的9个探空站的GTm进行改正并与探空站真值Tm作差, 进而分析精化模型的外符合精度, 统计结果见表 4(单位K)。
|
|
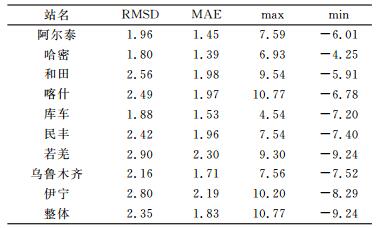
表 4 精化模型的外符合精度 Tab. 4 The precision of outer coincidence of the refined model |
从表 4可以看出, 精化后的GTm与真值Tm具有很好的一致性, 整体的RMSD为2.35 K, 相比精化之前减小4.73 K, MAE为1.83 K, 降低了4.86 K; 各站的RMSD、MAE都有明显的减少, 除库车、乌鲁木齐站外, 其他站的RMSD、MAE都减少了1.5 K以上, 和田、喀什、伊宁站下降更为明显; 各站的外符合精度与内符合精度相当, RMSD小于3 K, MAE在2.5 K以内, RMSD、MAE在各站分布均匀, 没有出现大的精度损失; 整体的误差最大值绝对值与误差最小值绝对值偏差基本在3 K左右, 误差绝对值最大值大部分在10 K以内, 最大为10.89 K, 与内符合精度表现一致。由此可知, 精化模型在内符合精度较高的同时也保证了较高的外符合精度, 精化模型具有较好的适应性, 具备较强的泛化能力。
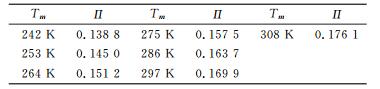
研究大气加权平均温度的最终目的是获得高精度的PWV。下面对经过精化后的GTm误差引起的PWV误差进行分析。据统计, 新疆地区2010~2014年9个探空站的Tm分布在[242, 300], 选择11 K作为递增梯度, 转换系数Π随加权平均温度Tm的变化如表 5所示。
|
|
表 5 转换系数Π随加权平均温度的变化 Tab. 5 The change of Π with Tm |
表 5显示, Tm增加或减小11 K, 引起Π的变化为0.006 2。假设天顶湿延迟没有误差, 则PWV的误差与转换系数Π误差之间的关系为:

|
(10) |
据计算, 新疆地区2010~2014年9个探空站的ZWD均小于100 mm, 即精化后的GTm取误差绝对值最大值10.89 K时, 所引起的误差约为0.62 mm, 可以满足精密遥感水汽含量的要求。因此, 根据精化模型的内外符合精度结果, 在各测站RMSD小于3 K、MAE小于2.5 K、误差绝对值最大值为10.89 K的情况下, 平均值法计算的GTm经精化模型改正后, 可以达到精密遥感水汽含量的要求。
4 结语利用GGOS Atmosphere提供的加权平均温度格网数据, 通过平均值法、最近点法、反距离加权法以及双线性插值法计算和分析新疆地区2010~2014年9个探空站的GTm, 通过建立精化模型对GTm进行改正。结果表明:1)反距离加权法计算GTm的整体精度最高, 平均值法与反距离加权法精度相当, 仅RMSD略大, 但精度分布更均匀、稳定; 2)平均值法得到的GTm整体小于由探空数据计算的Tm, 并存在半年周期和年周期特性; 3)利用考虑地理位置和年积日的GTm精化模型, 能有效提高平均值法计算GTm的精度, 得到的GTm可以满足精密遥感水汽含量的要求。
致谢: 衷心感谢美国怀俄明州立大学大气科学工程系和全球大地观测系统Atmosphere提供的数据资料!
| [1] |
Yao Y B, Zhu S, Yue S Q. A Globally Applicable, Season-Specific Model for Estimating the Weighted Mean Temperature of the Atmosphere[J]. J Geod, 2012, 86(12): 1 125-1 135 DOI:10.1007/s00190-012-0568-1
(  0) 0) |
| [2] |
于胜杰, 柳林涛. 水汽加权平均温度回归公式的验证与分析[J]. 武汉大学学报:信息科学版, 2009, 34(6): 741-744 (Yu Shengjie, Liu Lintao. Validation and Analysis of the Water-Vapor-Weighted Mean Temperature from Tm-Ts Relationship[J]. Geomatics and Information Science of Wuhan University, 2009, 34(6): 741-744)
(  0) 0) |
| [3] |
Yao Y B, Zhang B, Xu C Q, et al. Improved One/Multi-Parameter Models That Consider Seasonal and Geographic Variations for Estimating Weighted Mean Temperature in Ground-Based GPS Meteorology[J]. J Geod, 2014, 88(3): 273-282 DOI:10.1007/s00190-013-0684-6
(  0) 0) |
| [4] |
陈鹏, 陈家军. 利用NCEP再分析资料建立全球大气加权平均温度模型[J]. 大地测量与地球动力学, 2014, 34(3): 133-136 (Chen Peng, Chen Jiajun. Establishment of Global Atmospheric Weighted Average Temperature Model Using NCEP Reanalysis Data[J]. Journal of Geodesy and Geodynamics, 2014, 34(3): 133-136)
(  0) 0) |
| [5] |
Liu L L, Yao C L, Wen H Y. Empirical Tm Model in the Region of Guangxi[J]. Geodesy and Geodynamics, 2012, 3(4): 47-52 DOI:10.3724/SP.J.1246.2012.00047.1
(  0) 0) |
| [6] |
李国翠, 李国平, 杜成华, 等. 华北地区地基GPS水汽反演中加权平均温度模型研究[J]. 南京气象学院学报, 2009, 32(1): 80-86 (Li Guocui, Li Guoping, Du Chenghua, et al. Weighted Mean Temperature Models for Mapping Zenith Wet Delays onto Precipitable Water in North China[J]. Journal of Nanjing Institute of Meteorology, 2009, 32(1): 80-86 DOI:10.3969/j.issn.1674-7097.2009.01.010)
(  0) 0) |
| [7] |
王勇, 柳林涛, 郝晓光, 等. 武汉地区GPS气象网应用研究[J]. 测绘学报, 2007, 36(2): 141-145 (Wang Yong, Liu Lintao, Hao Xiaoguang, et al. The Application Study of the GPS Meteorology Network in Wuhan Region[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(2): 141-145 DOI:10.3321/j.issn:1001-1595.2007.02.005)
(  0) 0) |
| [8] |
王晓英, 宋连春, 戴仔强. 香港地区加权平均温度特征分析[J]. 南京信息工程大学学报:自然科学版, 2011, 3(1): 47-52 (Wang Xiaoying, Song Lianchun, Dai Ziqiang. Feature Analysis of Weighted Mean Temperature Tm in Hong Kong[J]. Journal of Nanjing University of Information Science and Technology:Natural Science Edition, 2011, 3(1): 47-52)
(  0) 0) |
| [9] |
Yao Y B, Zhang B, Yue S Q. Global Empirical Model for Mapping Zenith Wet Delays onto Precipitable Water[J]. J Geod, 2013, 87(5): 439-448 DOI:10.1007/s00190-013-0617-4
(  0) 0) |
| [10] |
姚宜斌, 张豹, 许超钤, 等. Tm-Ts的相关性分析及全球纬度相关的线性关系模型构建[J]. 科学通报, 2014, 59(9): 816-824 (Yao Yibing, Zhang Bao, Xu Chaoqian, et al. Analysis of the Global Tm-Ts Correlation and Establishment of the Latitude-Related Linear Model[J]. Chin Sci Bull, 2014, 59(9): 816-824)
(  0) 0) |
| [11] |
Boehm J, Werl B, Schuh H. Troposphere Mapping Functions for GPS and Very Long Baseline Interferometry from European Centre for Medium-Range Weather Forecasts Operational Analysis Data[J]. Journal of Geophysical Research:Solid Earth, 2006, 111(B2)
(  0) 0) |
| [12] |
许超钤, 姚宜斌, 张豹, 等. GGOS Atmosphere大气加权平均温度数据的精度检验与分析[J]. 测绘地理信息, 2014, 39(4): 13-16 (Xu Chaoqian, Yao Yibin, Zhang Bao, et al. Accuracy Analysis and Test on the Weighted Mean Temperature of the Atmosphere Grid Data Offered by GGOS Atmosphere[J]. Journal of Geomatics, 2014, 39(4): 13-16)
(  0) 0) |
| [13] |
Gutman S I, Benjamin S G. The Role of Ground-Based GPS Meteorological Observations in Numerical Weather Prediction[J]. GPS Solutions, 2001, 4(4): 16-24 DOI:10.1007/PL00012860
(  0) 0) |
| [14] |
Boehm J, Heinkelmann R, Schuh H. Short Note:A Global Model of Pressure and Temperature for Geodetic Applications[J]. J Geod, 2007, 81(10): 679-683 DOI:10.1007/s00190-007-0135-3
(  0) 0) |
| [15] |
Lagler K, Schindelegger M, Böhm J, et al. GPT2:Empirical Slant Delay Model for Radio Space Geodetic Techniques[J]. Geophysical Research Letters, 2013, 40(6): 1 069-1 073 DOI:10.1002/grl.50288
(  0) 0) |
| [16] |
张昊, 王琪洁, 朱建军, 等. 样本数据预处理对基于BP神经网络的高程转换的影响[J]. 大地测量与地球动力学, 2011, 31(2): 125-128 (Zhang Hao, Wang Qijie, Zhu Jianjun, et al. Influence of Sample Data Preprocessing on BP Neural Network-Based GPS Elevation Fitting[J]. Journal of Geodesy and Geodynamics, 2011, 31(2): 125-128)
(  0) 0) |
2. Guangxi Key Laboratory of Spatial Information and Geomatics, 319 Yanshan Street, Guilin 541006, China
 2017, Vol. 37
2017, Vol. 37