目前北斗卫星导航系统由5颗GEO卫星、6颗IGSO卫星和4颗MEO卫星组成。Shi等[1]采用两步法进行北斗卫星精密定轨, 得到GEO和IGSO的轨道重叠弧段精度为dm级。SLR单次测距精度己达cm级, 但由于其观测受天气条件及地面测站分布不均匀等因素影响, 难以实现对空间飞行器的全球、实时跟踪, 因此一般仅作为定轨手段之一, 或用于轨道精度检验。Otsubo等[2]通过实验发现, SLR观测值对GLONASS卫星的平均偏差为22 mm。Thaller等[3]分别估计了每个SLR测站的GPS/GLONASS系统偏差, 得到SLR测站对GPS/GLONASS卫星的系统偏差在5 cm以内。Hackei等[4]得到Galileo卫星的SLR检核系统偏差为5 cm左右, 并在卫星定轨时考虑该偏差进行分析比较。Deng等[5]统计了各个分析中心(COM/ESM/GBM/WUM)的北斗轨道产品的系统偏差。
目前尚未有联合SLR观测值和GNSS观测值进行北斗卫星精密定轨的研究(特别是GEO和IGSO卫星)。本文将主要进行这方面的研究。首先对北斗卫星GEO(C01)、IGSO(C08、C10)进行SLR残差检核; 然后联合SLR观测值进行定轨, 研究估计和不估计系统偏差对卫星轨道精度的影响; 最后对SLR测站与北斗卫星轨道之间的系统偏差进行讨论。
1 SLR观测模型修正及定轨方案SLR的原理是通过精密测定激光脉冲从测站到装有激光反射器的卫星的往返时间间隔τ, 从而得到某一时刻测站到卫星的距离ρ=cτ/2。激光测距的观测模型为[5-7]:
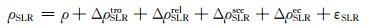
|
式中, ρSLR为SLR观测值; ρ为SLR测站至卫星的真实距离; ΔρSLRtro为对流层折射延迟误差; ΔρSLRrel为广义相对论效应误差; ΔρSLRscc为卫星质心补偿误差; ΔρSLRec为测站偏心误差; εSLR为SLR观测噪声。以上各改正项都能直接计算, 不需要引进待估参数[8-9]。本文在与GNSS联合定轨时, SLR观测方程的待估参数为卫星轨道6参数和光压系数。
2 精密定轨数据处理策略目前, 北斗GEO和IGSO卫星搭载激光反射镜的有Compass-G1、Compass-I3和Compass-I5。观测北斗卫星的SLR测站并不多, 本文选取SLR观测值数量相对较多的两个时间段对北斗卫星进行联合定轨。以武汉大学GNSS中心的PANDA软件为基础, 为提高轨道精度, 采用两步法定轨, 即先利用GPS精密星历进行PPP解算得到对流层、接收机钟差等公共参数的准确值, 然后在对北斗卫星定轨时将这些公共参数固定。主要定轨策略如表 1所示。
|
|
表 1 GNSS/SLR定轨策略 Tab. 1 Orbit determination strategy for combined solution |
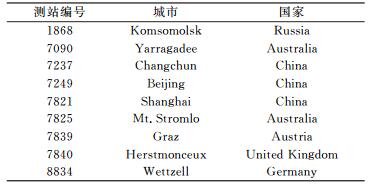
表 2给出了实验期间对北斗卫星C01、C08和C10进行观测的SLR跟踪测站, 图 1给出了每个测站在实验期间对应每颗星的标准数据点数量。目前跟踪北斗卫星的SLR测站较少, 从图 1可知, 实验期间数据点相对较多的有4、5个测站。为研究SLR观测值对北斗卫星定轨的影响, 选取2014-06~2015-12数据量较多的时间段(约3个月)进行实验。
|
|
表 2 计算时间内跟踪北斗GEO/IGSO卫星的SLR测站 Tab. 2 SLR tracking stations for BDS GEO and IGSO satellites during experimental period |

|
图 1 2014/305~2014/363, 2015/213~2015/254期间北斗卫星SLR观测值数量 Fig. 1 Numbers of SLR normal points for each satellite during 2014/305-2014/363 and 2015/213-2015/254 |
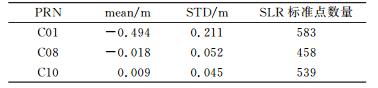
为了确定联合定轨的研究中引入系统偏差参数的方式, 主要分析仅采用GNSS定轨时北斗卫星轨道与SLR观测值的偏差。根据§2介绍的定轨策略, 得到2014/305~2014/363、2015/213~2015/254这两个时间段内卫星的3 d解轨道。图 2给出了计算时间内3颗卫星的SLR残差值。表 3给出了计算时间内3颗卫星SLR残差的平均值和均方差及有效标准点数量。

|
图 2 SLR检核北斗卫星轨道残差 Fig. 2 SLR residual series of C01, C08 and C10 |
|
|
表 3 各天SLR残差均值和均方差统计 Tab. 3 The average and standard deviation for SLR residuals |
从以上结果可知, C01卫星的轨道结果与SLR观测值存在约50 cm的系统偏差。Lou等[10]、Steigenberger等[11]和Zhao等[12]分别采用不同的光压模型对C01卫星进行定轨分析, 结果显示, 不同光压模型得到的轨道的SLR残差平均值各不相同。Steigenberger等只估计了ECOM模型中指向太阳方向的光压参数, 得到的SLR残差平均值最小, 为-31.9 cm。因此推测, 本文得到的50 cm的系统偏差可能是由于GEO卫星的动力学模型不准确或者其他不确定因素导致的, 具体原因有待进一步研究。C08与C10卫星轨道与SLR观测值的偏差在2 cm以内。为进一步分析SLR残差特性, 图 3分别给出了计算时间内每个测站的SLR残差均值。由于1868测站在本文实验时间内对3颗卫星的观测值数量很少, 后面的计算将忽略该测站。从图 3可知, 每个测站之间的偏差存在较大差异, 因此, 在联合SLR观测值进行定轨引入系统偏差时应对每个测站分别引入参数。

|
图 3 各测站SLR残差平均值 Fig. 3 The mean value for SLR residuals of each tracking station |
采用SLR与GNSS观测值联合定轨, 分析SLR观测值对北斗卫星轨道精度的影响及北斗卫星的系统偏差。通过前面的分析可知, SLR残差对北斗卫星均存在一定的偏差且每个测站均不同, 因此采用SLR观测值定轨时需要考虑该偏差。根据对系统偏差的估计方法设计如表 4所示的实验方案。
|
|
表 4 实验方案 Tab. 4 Experimental scheme |
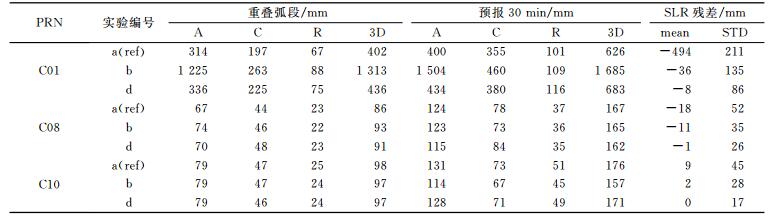
本文定轨弧段均为3 d解, 采用重叠弧段(overlap)和预报30 min弧段(prediction)的轨道精度来评价定轨精度。重叠轨道是比较两组连续解算轨道的重叠弧段部分(2 d)的轨道差异。由于3 d解第2天的轨道精度最高, 因此预报30 min的轨道弧段是比较第1组轨道的预报轨道前30 min与第3组轨道第2天的轨道差异, 最后根据轨道差异的RMS来评价定轨精度。重叠弧段和预报弧段示意图见图 4。

|
图 4 轨道重叠弧段/预报弧段示意图 Fig. 4 Overlap comparison of orbit determination and prediction |
表 5对以上3组实验结果进行了统计, 给出了C01、C08和C10卫星在每组实验重叠弧段、预报30 min弧段的切向、法向、径向及三维平均RMS值, 并给出了每组实验与SLR检核残差的平均值和均方差。结果显示, 由于C01卫星的SLR残差平均偏差达到50 cm, 若不考虑该偏差, 直接采用SLR观测值与GNSS观测值联合定轨会使整体轨道偏离(b); 若需要引入SLR观测值联合定轨, 则应对每个SLR测站引入系统偏差参数来吸收系统差, 此时得到的轨道精度略差于仅采用GNSS观测值的定轨结果(a), 其SLR检核残差明显变小。需要指出的是, 对于C01卫星而言, 加入SLR数据后, 采用方案d时卫星轨道的重叠弧段和预报轨道精度并没有得到改善。从§3的分析可知, C01卫星的轨道结果与SLR观测值之间存在的较大系统偏差(约50 cm), 可能是由于GEO卫星的动力学模型不准确所致。若GEO卫星的动力学模型不准确(光压模型不准确或者其他因素), 则卫星轨道与SLR各测站观测值之间的系统偏差将不会是一个常数, 可能会随着卫星帆板与太阳入射方向之间的变化而变化, 或随着SLR观测站与卫星之间的几何关系变化而变化等。这时如果将系统偏差作为常数引入, 不一定能提高卫星轨道精度, 具体原因有待进一步研究。
|
|
表 5 各组实验轨道精度比较 Tab. 5 Orbit comparison of each experiment |
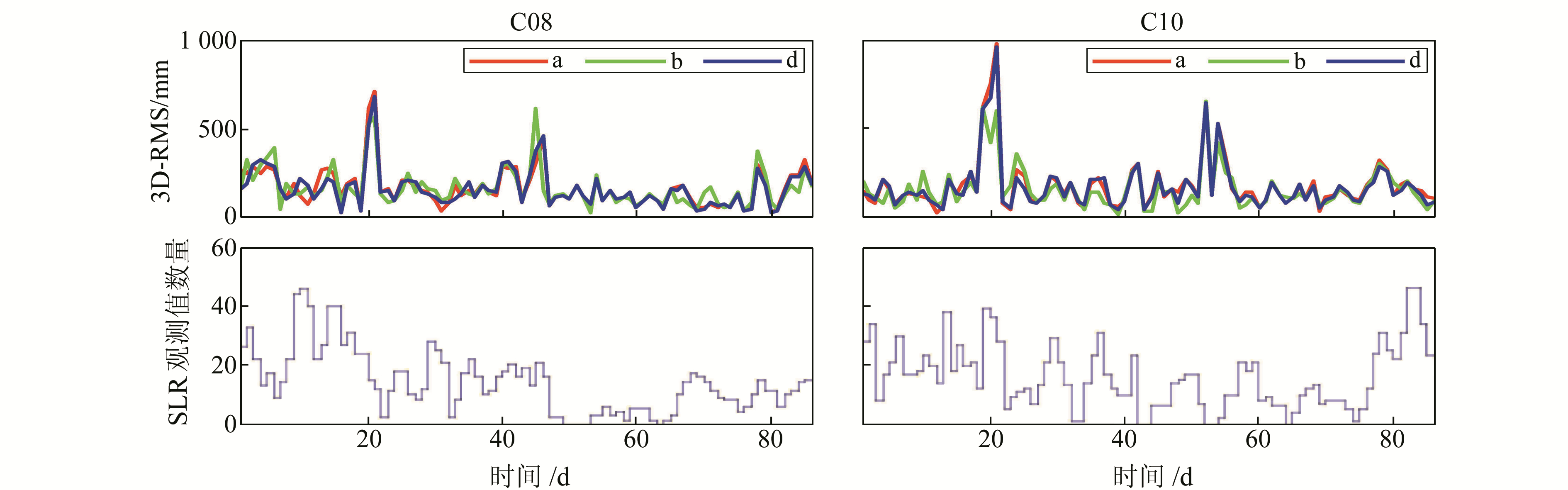
与C01卫星相比, C08和C10卫星仅采用GNSS观测值时SLR残差偏差较小, 在5 cm以内, 加入SLR观测值时没有引起轨道偏离。C08和C10卫星加入SLR观测值定轨后, 对重叠弧段的轨道精度没有改善, 但数据显示, 即使只有少量的SLR观测值, 对预报弧段的3个方向的精度均有微小的改善。这可能是因为卫星在切向和法向的力模型误差较大, 虽然SLR观测值主要在径向, 但能够增强径向解的强度, 从而能更精确地估计力模型。为了进一步分析C08和C10卫星轨道精度与SLR观测值的关系, 图 5给出了仅采用GNSS观测值(a), 不估计(b)/估计(d)系统偏差这3组实验下, C08和C10卫星预报弧段的三维RMS以及对应的SLR观测值数量。
|
图 5 C08和C10卫星三维预报轨道精度比较以及对应轨道弧段的SLR标准点数量 Fig. 5 Prediction orbit comparison and number of SLR normal points for C08 and C10 |
从图 5可知, 估计系统偏差时, 卫星预报30 min轨道弧段精度与仅采用GNSS观测值时的轨道符合较好。对C08卫星, 联合定轨时应估计系统偏差; 对C10卫星, SLR残差平均值仅为9 mm, 基本不存在系统差, 同时SLR观测值数量较少, 引入系统偏差会增加未知数的个数从而降低解的强度, 导致估计系统偏差(d)的轨道精度比不估计系统偏差(b)的精度低。因此, C10卫星可以不估计系统偏差, 若以后增加新的测站或测站观测频率发生变化, 可能需要重新实验。同时, 从图 5可知, SLR观测值数量与预报弧段精度并没有明显的关系, 这主要是因为SLR观测值对卫星轨道精度的影响不仅与观测值数量有关, 还与测站分布以及时间分布等多个因素有关。
4.2 SLR测站系统偏差分析通过对SLR残差及SLR与GNSS观测值联合定轨的分析发现, SLR测站对于每颗卫星均存在一定的系统偏差, 本节主要分析SLR测站对北斗GEO/IGSO卫星的系统偏差大小。
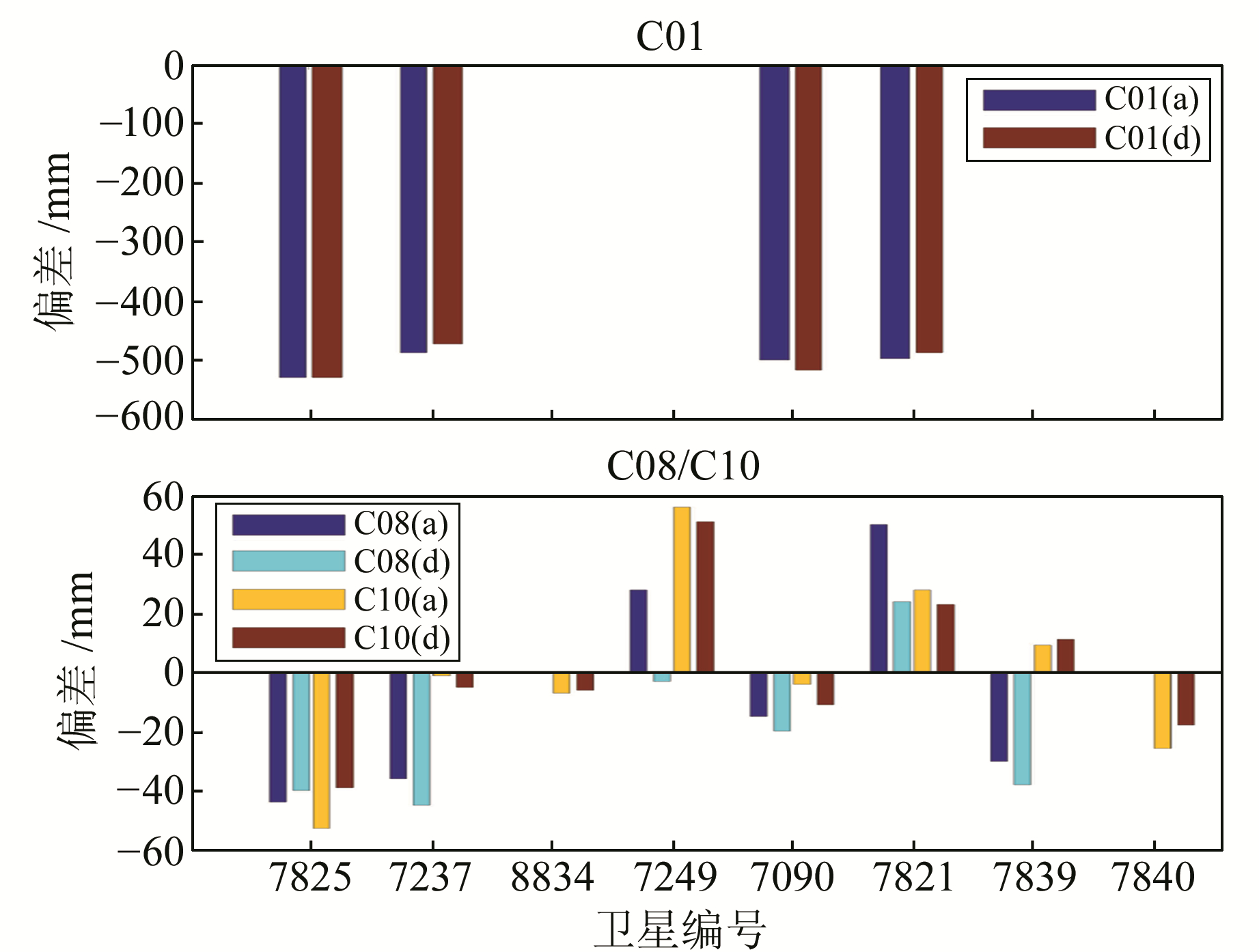
仅采用GNSS定轨时, 根据SLR检核残差可以计算得到每个SLR测站对每颗卫星的残差均值, 当SLR观测值数量足够多时, 该平均值可近似认为是系统偏差。同时本文的实验(d)在联合SLR观测值定轨时分别估计了每个测站对每颗卫星的系统偏差。图 6给出了这两种方法计算得到的系统偏差。
|
图 6 卫星系统偏差比较 Fig. 6 Comparison of SLR range biases |
从图 6可知, 大部分测站两种方法得到的系统偏差值相差不大, 个别测站得到的系统偏差有较大差异, 这主要是由于该站的SLR观测值较少, 计算出来的系统偏差没有很强的代表性。
5 结语本文主要分析了SLR观测值对北斗GEO/IGSO卫星定轨精度的影响以及北斗GEO/IGSO卫星的系统偏差。首先分析了仅采用GNSS观测值定轨时北斗卫星(GEO/IGSO)的SLR残差, SLR测站对于每颗卫星均存在一定的系统偏差且互不相同, 在联合SLR/GNSS定轨时需要考虑这一因素。联合定轨时得到如下结论:1)C01卫星加入SLR观测值定轨时, 需要引入系统偏差参数, 否则会严重影响轨道重叠弧段的精度; 2)C08和C10卫星加入SLR观测值定轨时, 估计/不估计系统偏差对计算轨道部分没有明显影响, 对预报轨道部分有一定程度的改善, 估计系统偏差时的轨道精度与仅采用GNSS定轨的轨道精度最相符; 3)实验结果表明, C08卫星定轨最好估计系统偏差, C10卫星定轨时可以不估计系统偏差, 这主要是由目前每颗卫星对应测站偏差的大小决定的, 若以后北斗卫星SLR测站数量增加或观测数量发生变化, 可能需要重新实验; 4)仅利用GNSS定轨得到的SLR检核北斗轨道残差均值与估计得到的系统偏差均值相当。目前的实验分析结果表明, 在现有的GNSS观测数据基础上加入SLR跟踪数据进行北斗卫星的精密定轨, 对轨道精度的改善作用有限。其主要原因可能是现在北斗卫星的SLR观测站稀少、观测值数量比较少, 待以后SLR观测值数量增加, 可进行进一步的分析研究。
| [1] |
Shi C, Zhao Q L, Li M, et al. Precise Orbit Determination of Beidou Satellites with Precise Positioning[J]. Sci China Earth Sci, 2012, 55(7): 1 079-1 086 DOI:10.1007/s11430-012-4446-8
(  0) 0) |
| [2] |
Otsubo T, Apleby G M, Gibbs P. GLONASS Laser Ranging Accuracy with Satellite Signature Effect[J]. Surv Geophys, 2001, 22(5-6): 509-516
(  0) 0) |
| [3] |
Thaller D, Dach R, Seitz M, et al. Combination of GNSS and SLR Observations Using Satellite Co-Locations[J]. J Geod, 2011, 85(5): 257-272 DOI:10.1007/s00190-010-0433-z
(  0) 0) |
| [4] |
Hackel S, Steigenberger P, Hugentobler U, et al. Galileo Orbit Determination Using Combined GNSS and SLR Observations[J]. GPS Solut, 2015, 19(1): 15-25 DOI:10.1007/s10291-013-0361-5
(  0) 0) |
| [5] |
Deng Z, Zhao Q, Springer T, et al.Orbit and Clock Determination-Beidou[C].IGS Workshop, Pasadena, 2014
(  0) 0) |
| [6] |
Urschl C, Beutler G, Gurtner W, et al. Contribution of SLR Tracking Data to GNSS Orbit Determination[J]. Advances in Space Research, 2007, 39(10): 1 515-1 523 DOI:10.1016/j.asr.2007.01.038
(  0) 0) |
| [7] |
Urschl C, Gurtner W, Hugentobler U, et al. Validation of GNSS Orbits Using SLR Observations[J]. Advances in Space Research, 2005, 36(3): 412-417 DOI:10.1016/j.asr.2005.03.021
(  0) 0) |
| [8] |
Zelensky N P, Lemoine F G, Ziebart M, et al. DORIS/SLR POD Modeling Improvements for Jason-1 and Jason-2[J]. Advances in Space Research, 2010, 46(12): 1 541-1 558 DOI:10.1016/j.asr.2010.05.008
(  0) 0) |
| [9] |
秦显平, 焦文海, 程芦颖, 等. 利用SLR检核CHAMP卫星轨道[J]. 武汉大学学报:信息科学版, 2005, 30(1): 38-41 (Qin Xianping, Jiao Wenhai, Cheng Luying, et al. Evaluation of CHAMP Satellite Orbit with SLR Measurements[J]. Geomatics and Information Science of Wuhan University, 2005, 30(1): 38-41)
(  0) 0) |
| [10] |
Lou Y D, Liu Y, Shi C, et al. Precise Orbit Determination of Beidou Constellation Based on BETS and MGEX Network[J]. Scientific Reports, 2014, 4(8): 4 692
(  0) 0) |
| [11] |
Steigenberger P, Hugentobler U, Hauschild A, et al. Orbit and Clock Analysis of Compass GEO and IGSO Satellites[J]. J Geod, 2013, 87(6): 515-525 DOI:10.1007/s00190-013-0625-4
(  0) 0) |
| [12] |
Zhao Q L, Guo J, Li M, et al. Initial Results of Precise Orbit and Clock Determination for COMPASS Navigation Satellite System[J]. J Geod, 2013, 87(5): 475-486 DOI:10.1007/s00190-013-0622-7
(  0) 0) |
 2017, Vol. 37
2017, Vol. 37