2. 武汉大学GNSS中心, 武汉市珞喻路 129号, 430079;
3. 武汉大学地球空间环境与大地测量教育部重点实验室, 武汉市珞喻路 129号, 430079
GPS/BDS融合变形监测较单GPS监测可增加卫星数, 改善几何图形结构、可用性、可靠性和监测精度等, 已成为GNSS变形监测的新趋势[1]。小区域的GPS/BDS变形监测中, 测站间的多路径误差不具有强空间相关性, 无法像电离层、对流层等强相关性误差可通过双差方式来消除, 加之多路径效应对载波相位观测值的影响最大可以达到几个cm[2], 其已成为制约提高GNSS实时变形监测精度的主要误差源。针对变形监测数据中多路径误差的削弱, 目前主要是在坐标域内根据多路径误差的周期特性建立参考天的多路径误差时间序列模型, 再通过恒星日滤波方法削弱后续天的多路径误差[3-6]。这种方法可以在一定程度上分离出噪声与低频多路径误差, 但往往忽略了高频多路径误差, 也未对GPS/BDS融合监测序列中的多路径误差削弱方法等开展较多的研究。其次是在观测值域内削弱多路径误差[7-9], 提取参考天模糊度固定后的相位残差, 根据卫星的方位角和高度角确定每颗卫星载波和伪距观测值多路径误差改正数。该方法实现较为困难, 且不利于实时处理。本文将针对GPS/BDS融合实时变形监测的应用场景, 通过对单差观测值中的多路径误差和高频随机噪声的特性分析, 给出合理的去噪及多路径时序模型构建方法, 以期减小实时监测序列中的多路径误差影响, 提高GNSS实时监测精度。
1 多路径特性与GPS系统全部由MEO卫星组成不同, BDS的星座由GEO、IGSO和MEO卫星组成, 且MEO与其他两类卫星的回归周期不同, GEO、IGSO大约为1个恒星日, 而MEO卫星为7个恒星日[9]。为分析GPS/BDS监测中多路径误差对相位观测值影响的大小及其周期特性, 本文参考文献[9], 将卫星的双差残差映射到单差残差, 进而提取了2015年第350~352天某GNSS变形工程中的某监测点全天观测的GPS的G01卫星、BDS的C01卫星(GEO)和C07卫星(IGSO)第1个频点上的相位单差残差(图 1)。同时单独分析了C12卫星(MEO)2015年第342~344天和2015年第349~351天单差残差数据(图 2)。此单差残差可认为只包含多路径误差以及随机噪声的影响[7], 同时对残差进行相应的平滑处理, 便于更好地对对应天多路径误差进行相关性分析。

|
图 1 BDS C01、C07和GPS G01卫星相位单差的残差序列 Fig. 1 Single difference residual sequences of BDS C01, C07 and GPS G01 |

|
图 2 BDS C12卫星相位单差的残差序列 Fig. 2 Single difference residual sequences of BDS C12 |
为方便与第1天比较, 根据GPS卫星和BDS GEO、IGSO卫星的回归周期, 对图中第2天和第3天的横坐标分别减去86 400 s和172 800 s。图 1、2中相关天共同中断的数据主要跟各自的卫星运动特性有关, 该时段接收机无此卫星信号。另外, 类似于C07第350天中(某单天)某小时段数据缺失, 可能是由于接收机观测不稳定或者数据传输问题导致的。
选取对应天同步连续观测较长时段的残差进行相关性分析, 结果见表 1。
|
|
表 1 卫星单差残差相关性分析 Tab. 1 Correlation coefficients of satellite single difference residuals |
从图 1和表 1可以看出, BDS的GEO和IGSO以及GPS卫星的单差残差序列中相邻天相关性较大, 说明多路径误差具有逐日重复的特点, 且其重复周期与相应的卫星回归周期基本一致; BDS的MEO卫星的多路径误差变化规律不具有日重复性, 而时隔7 d具有较强的相关性, 也基本与其回归周期一致。
由于BDS的MEO卫星回归周期不是一个恒星日, 鉴于实际GPS/BDS监测中每个历元观测到的BDS MEO卫星只有1~2颗, 且观测时长较短, 对定位精度和卫星几何图形结构强度贡献有限, 因此为了充分利用在GPS监测中应用较为成熟的恒星日滤波算法, 在后续的BDS处理分析中只考虑GEO及IGSO卫星。同时针对不同卫星周期不一样的特点, 本文求取了观测数据中相邻天基准站和流动站共视卫星的平均回归周期来获取最佳的平移周期, 以此克服传统的多路径误差周期确定方式不严谨的缺点[6], 便于提取坐标序列中最优的多路径综合误差序列。
2 EMD小波阈值降噪算法对于小区域的GNSS监测序列, 均值化后的坐标序列主要包含变形趋势、高频随机噪声以及多路径信号。为了分析监测序列的变形特征, 需要自适应地剔除序列中的高频随机噪声, 消除或尽可能地削弱多路径误差的影响。鉴于此, 本文根据EMD算法的特点, 采用EMD对GPS/BDS实时监测的坐标序列予以分解, 分离出高频噪声, 并根据分解后的若干固有模态函数和下文的算法构建多路径误差序列模型。
EMD实际上是一个从高频至低频的筛分过程, 分解的若干基本信号称为固有模态函数(intrinsic mode function, IMF)[10]。从现有的研究结果来看, EMD筛选分解出的IMF高频模态分量中仍有部分有用信号[11], 其多路径信号对载波相位观测值的影响在一般情况下能达到1~2 mm[11]。但传统的EMD去噪会将高频IMF分量直接舍弃, 从而损失了高频IMF中的有用信息。因此, 本文提出组合EMD与小波阈值去噪的方法(简称EW), 借助小波阈值消噪提取高频模态分量中的多路径信息, 同时完全保留低频模态分量中的低频多路径信号。该方法不足之处是小波基的选择和分解层数的确定需要通过多次实验获取[12]。对于模态分量中低频信号层的确定, 本文参考罗飞雪等[13]提出的交叉证认的算法获取信号层。该证认方法可以自适应地选择IMF中的信号层数。EW降噪算法流程见图 3。

|
图 3 EW去噪构建多路径模型算法流程 Fig. 3 Flow chart of EW denoising algorithm |
为了验证上述算法的有效性, 选取某矿区GNSS变形监测项目中的某监测站和对应基准站的GPS/BDS观测数据进行实验。对应的同步观测时间为2015年第349~351天12:00~16:10, 数据采样间隔为5 s, 共3 000个历元, 所用接收机为司南K501 GPS/BDS双频接收机, 基准站和流动站距离小于1.53 km, 高差小于28 m。所用基线数据的基准站位于小山头之上, 观测墩按设计要求进行建造埋设, 非常稳定。监测站位于矿区之内, 由于该矿区为一个老矿, 根据水准仪等手段的监测结果认为其较为稳定。同时, 对这些观测数据采用商业化的LGO软件按照2 h进行时段整体解处理。从处理的结果来看, 水平方向和高程方向也不存在较为明显的变形趋势, 因此监测点在上述分析时段内较为稳定, 基本不存在变形。
在进行分析前, 首先基于作者自主研发的GPS/BDS实时变形监测软件RTGM解算每个历元的基线分量, 之后对各天获得的坐标位移序列减去第349天位移序列的均值。均值化处理后的时间序列可认为只受到多路径和高频随机噪声以及变形趋势的影响。限于篇幅, 只将该项目监测序列中高程方向的数据处理结果进行绘图分析。
通过以下流程验证本文算法的有效性。首先通过EMD以及EW两种方法提取第1天实验数据的精确的多路径时间序列模型, 再根据周期内求差的方式即恒星日滤波算法, 对后续天的坐标序列进行相应的多路径误差改正。从图 4可以看出, 连续3 d原始U方向具有一定重复性, 说明坐标序列中受多路径误差影响较大, 另外两种方法去噪后的序列都较为平滑, 高频随机噪声得到有效剔除。图 5为第2天和第3天经第1天提取的多路径模型改正后的时间序列。可以看出, 经EW提取的多路径模型改正后的坐标序列较EMD更为平滑, 多路径误差削弱更充分。进行多次实验来确定EW中小波基的选取, 结果表明, 采用db8小波基处理效果较好, 消噪后的坐标时间序列与原始坐标时间序列相关性较大, 精度更高。

|
图 4 基于不同方法降噪后的坐标序列 Fig. 4 Denoised coordinates with different methods |
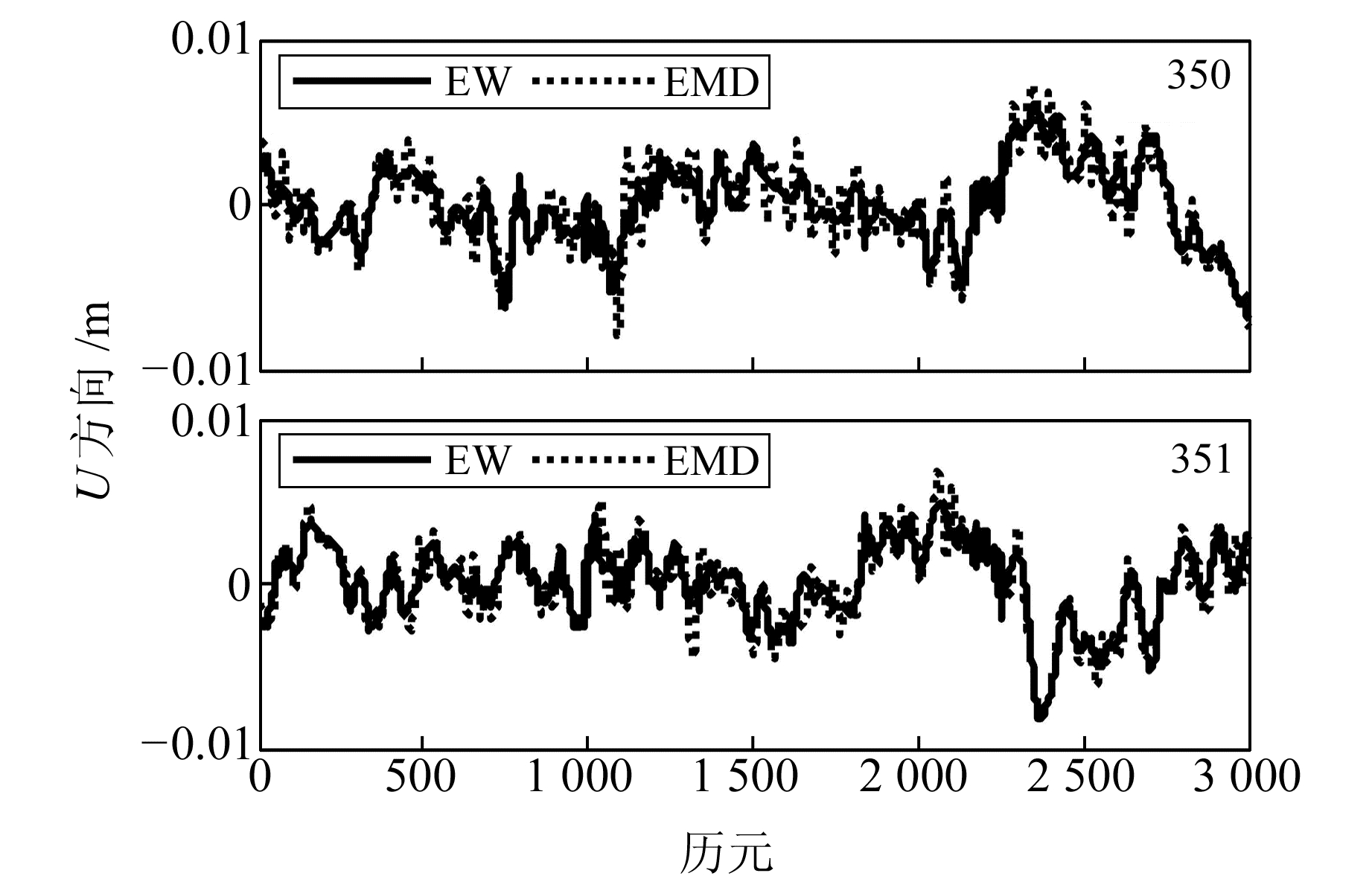
|
图 5 不同方法下恒星日滤波后的坐标系列 Fig. 5 Sideral filtering coordinates with different denoising methods |
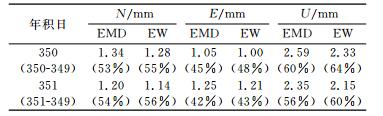
表 2~4定量分析了两种方法处理前后坐标时间序列的标准差STD、相关系数, 以及经第1天多路径模型改正后的STD, 以此作为两种方法优劣的评价标准。从表 2中可以看出, 原始坐标序列与去噪后序列的STD相差较小, 说明坐标序列中多路径误差占主要部分。表 3中原始坐标序列3个方向的对应天相关性能达到0.7左右, 说明相邻天多路径误差具有很强的重复性, 当经过滤波去噪后, 相关性提高12%左右, 且EW去噪后相关性较EMD稍好, 更能充分地提取多路径模型。表 4说明EMD和EW都能较好地提取多路径改正模型, 改正后的坐标序列3个方向的STD较之前减少了50%, 且EW总体上较EMD稍好。表 4中参考天对第2天的改正效果较第3天好, 一定程度上说明参考天的多路径模型改正效果依赖于对应天待改正坐标序列和参考天多路径误差的相关性。
|
|
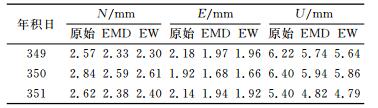
表 2 坐标序列滤波前后的STD Tab. 2 STD of raw and denoised coordinates |
|
|
表 3 坐标序列滤波前后的相关系数 Tab. 3 Correlation coefficients between consecutive multipath sequences |
|
|
表 4 经多路径模型改正后坐标序列的STD值和改正效果 Tab. 4 STD of coordinates before and after multipath corrections are applied |
本文针对GPS/BDS坐标序列中的多路径误差呈现出的日周期性变化特征, 采用了EMD以及EW两种方法分别滤除坐标序列中的高频随机噪声, 构建多路径误差模型, 进而根据共视卫星的平均周期进行恒星日滤波, 以削弱后续天的多路径误差的影响。从实际数据的处理分析结果来看, 可以获得以下结论:
1) EMD可以较好地削弱GPS/BDS实时监测坐标序列中的随机噪声, 是一种不受限于数据的自适应去噪算法, 基于此方法能构建出参考天的多路径效应误差模型, 进而实现对后续天的多路径效应误差的改正。对于本文算例来说, 可提高变形监测精度50%左右。
2) 当选取合适的小波基以及分解层数后, EW可在EMD算法的基础上更充分地提取高频模态分量中的多路径信号; 滤波后的坐标序列标准差较单EMD更小, 前后2 d的相关性更强, 基于此方法构建的多路径误差模型能更好地改正后续天的多路径误差, 获得比EMD稍好的精度。
为了方便处理, 本文没有考虑回归周期为7 d的BDS MEO卫星, 这会在一定程度上影响监测精度。随着BDS全球化的建设, 未来将会有更多的MEO卫星供用户使用, 所以后续的工作可以基于每颗卫星在观测值域构建多路径模型, 以更好地削弱GEO/IGSO/MEO三类不同回归周期的卫星的多路径误差。
| [1] |
敦煜.BDS/GPS实时变形监测数据处理方法及软件实现[D].武汉: 武汉大学, 2015 (Dun Yu.Research on the Method of the BDS/GPS Real-Time Deformation Monitoring Data Processing and Software Implementation[D].Wuhan: Wuhan University, 2015)
(  0) 0) |
| [2] |
李征航. GPS测量与数据处理[M]. 武汉: 武汉大学出版社, 2010 (Li Zhenghang. GPS Surveying and Data Processing[M]. Wuhan: Wuhan University Press, 2010)
(  0) 0) |
| [3] |
戴吾蛟, 丁晓利, 朱建军, 等. 基于经验模式分解的滤波去噪法及其在GPS多路径效应中的应用[J]. 测绘学报, 2006, 35(4): 321-327 (Dai Wujiao, Ding Xiaoli, Zhu Jianjun, et al. EMD Filter Method and Its Application in GPS Multipath[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(4): 321-327 DOI:10.3321/j.issn:1001-1595.2006.04.005)
(  0) 0) |
| [4] |
钟萍, 丁晓利, 郑大伟. CVVF方法用于GPS多路径效应的研究[J]. 测绘学报, 2005, 34(2): 161-167 (Zhong Ping, Ding Xiaoli, Zheng Dawei. Study of GPS Multipath Effects with Method of CVVF[J]. Acta Geodaetica et Cartographica Sinica, 2005, 34(2): 161-167 DOI:10.3321/j.issn:1001-1595.2005.02.013)
(  0) 0) |
| [5] |
Agnew D C, Larson K M. Finding the Repeat Times of the GPS Constellation[J]. GPS Solutions, 2006, 11(1): 71-76 DOI:10.1007/s10291-006-0038-4
(  0) 0) |
| [6] |
Choi K. Modified Sidereal Filtering:Implications for High-Rate GPS Positioning[J]. Geophysical Research Letters, 2004, 31(22)
(  0) 0) |
| [7] |
Zhong P, Ding X L, Yuan L G, et al. Sidereal Filtering Based on Single Differences for Mitigating GPS Multipath Effects on Short Baselines[J]. Journal of Geodesy, 2010, 84(2): 145-158 DOI:10.1007/s00190-009-0352-z
(  0) 0) |
| [8] |
Dong D, Wang M, Chen W, et al. Mitigation of Multipath Effect in GNSS Short Baseline Positioning by the Multipath Hemispherical Map[J]. Journal of Geodesy, 2016, 90(3): 255-262 DOI:10.1007/s00190-015-0870-9
(  0) 0) |
| [9] |
Ye S R, Chen D Z, Liu Y Y, et al. Carrier Phase Multipath Mitigation for Beidou Navigation Satellite System[J]. GPS Solutions, 2015, 19(4): 545-557 DOI:10.1007/s10291-014-0409-1
(  0) 0) |
| [10] |
Huang N E, Wu M L C, Long S R, et al. A Confidence Limit for the Empirical Mode Decomposition and Hilbert Spectral Analysis[J]. Proceedings of the Royal Society A:Mathematical, Physical and Engineering Sciences, 2003, 459(2 037): 2 317-2 345
(  0) 0) |
| [11] |
Souza E M, Monico J F G. Wavelet Shrinkage:High Frequency Multipath Reduction from GPS Relative Positioning[J]. GPS Solutions, 2004, 8(3): 152-159 DOI:10.1007/s10291-004-0100-z
(  0) 0) |
| [12] |
Azarbad M R, Mosavi M R. A New Method to Mitigate Multipath Error in Single-Frequency GPS Receiver with Wavelet Transform[J]. GPS Solutions, 2014, 18(2): 189-198 DOI:10.1007/s10291-013-0320-1
(  0) 0) |
| [13] |
罗飞雪, 戴吾蛟, 伍锡锈. 基于交叉证认的EMD滤波及其在GPS多路径效应中的应用[J]. 武汉大学学报:信息科学版, 2012, 37(4): 450-453 (Luo Feixue, Dai Wujiao, Wu Xixiu. EMD Filtering Based on Cross-Validation and Its Application in GPS Multipath[J]. Geomatics and Information Science of Wuhan University, 2012, 37(4): 450-453)
(  0) 0) |
2. GNSS Research Centre, Wuhan University, 129 Luoyu Road, Wuhan 430079, China;
3. Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan University, 129 Luoyu Road, Wuhan 430079, China
 2017, Vol. 37
2017, Vol. 37