2. 同济大学测绘与地理信息学院, 上海市四平路1239号, 200092;
3. 桂林理工大学测绘地理信息学院, 桂林市雁山街319号, 541006
GNSS已广泛应用于机载、车载以及其他位置与速度测量应用中[1], 可以快速、准确地确定运动载体的位置及速度。通常情况下, 当采用单一卫星定位系统时, 利用4颗卫星的伪距观测值就可以实现定位[2]。传统的抗多路径误差导航定位算法主要是基于GPS伪距观测值的抗差估计[3], 在城市稠密地区, 当观测数据有限或多路径误差较大时, 难以有效地消除和减少误差影响, 不能满足实际应用的要求。目前BDS已经正式提供中国及其周边地区的导航定位服务, 这无疑将提高卫星定位的有效性和精度。为此, 本文拟研究一种基于GPS/BDS伪距观测值和对多路径误差敏感度较低的多普勒观测值的导航模型, 结合抗差自适应卡尔曼滤波模型, 有效改善多路径环境下的定位精度。最后, 通过在上海市区的GPS/BDS车载导航实验, 验证了本文算法的有效性。
1 伪距与多普勒定位模型 1.1 伪距观测模型单系统t时刻伪距观测方程可表示为[4]:
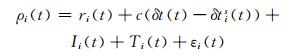
|
(1) |
式中, ρi(t)为对卫星i的伪距观测值; ri(t)为卫星i与测站的几何距离; c为光速; δt(t)为接收机钟差; δtis(t)为卫星i的钟差; Ii(t)为电离层延迟; Ti(t)为对流层延迟; εi(t)为伪距测量噪声。解算时, 对电离层误差和对流层误差进行模型改正。式(1)按泰勒级数展开为:
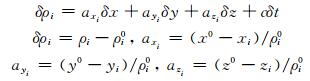
|
(2) |
式中, (x0, y0, z0)为测站近似位置向量; (xi, yi, zi)为卫星i的坐标; ρ0为对应测站至卫星的距离。当观测N颗卫星时, 观测模型的矩阵形式为:
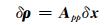
|
(3) |
式中, App为观测N颗卫星的系数矩阵; δρ为观测量矩阵; δx为待求矩阵[4]。
根据式(3), 采用GPS/BDS组合观测值时的观测模型可以表示为:

|
(4) |
式中, G、B分别表示GPS和BDS系统; A′ ppG为GPS卫星和测站之间的几何观测矩阵的前3列; A′ppB为BDS卫星和测站之间的几何观测矩阵的前3列; 1、0表示各元素为1、0的N维列向量; δx′ =[δx δy δz cδtG cδtB]T中各分量分别为x、y、z方向的位置改正数、GPS和BDS系统的接收机钟差。考虑到GPS和BDS伪距观测值精度相当, 根据最小二乘原理, 可得位置改正数和钟差:
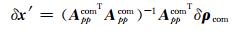
|
(5) |
当接收机载体和卫星之间存在相对运动时, 接收机接收到的载波信号频率与卫星发射的载波信号的频率是不同的, 其间的频率差值称为多普勒频移, 表达式为[5-6]:
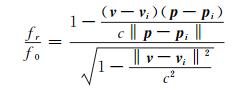
|
(6) |
式中, fr为接收机接收到的卫星信号频率; f0为卫星的信号频率; p、v分别为测站的位置和速度向量; pi、vi分别为卫星i的位置和速度向量; c为光速。考虑到卫星与用户载体的相对运动速度远小于光速, 式(6)可以简化为[5]:
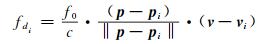
|
(7) |
式中, fdi为卫星i的多普勒观测值。式(7)按泰勒级数展开可得:
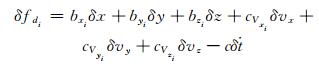
|
(8) |
式中, (x0, y0, z0, vx0, vy0, vz0)为近似位置及速度向量, 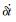
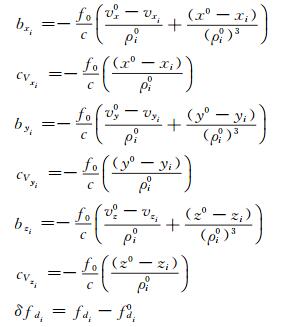
|
式(8)中包含了x、y、z方向的位置改正数(δx, δy, δz)、速度改正数(δvx, δvy, δvz)及接收机钟速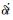
GPS/BDS伪距与多普勒联合误差方程可写为:

|
(9) |
式中,
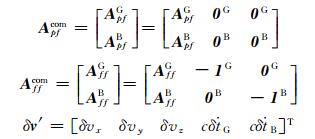
|
式中, Apf、Aff分别表示多普勒方程的位置系数阵和速度系数阵。上式包含了x、y、z方向的3个位置改正数(δx, δy, δz)、3个速度改正数(δvx, δvy, δvz)及GPS和BDS系统的2个接收机钟差(δtG, δtB)和2个钟速(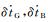
根据式(9), 考虑到伪距与多普勒观测值观测精度的不同, 最小二乘解为:
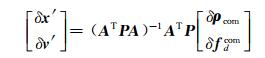
|
(10) |
式中, A为式(9)系数阵; P为两类观测值权阵。
2 抗差自适应滤波模型本文采用常速模型, 其动态方程为[7]:
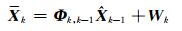
|
(11) |
式中, Xk为k时刻的预测状态向量, 含10个待求参数; Φk, k-1为状态转移矩阵; 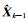
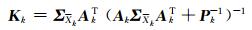
|
(12) |
式中, Kk为卡尔曼增益矩阵; ΣXk为Xk的协方差矩阵。k时刻的状态参数估值为:
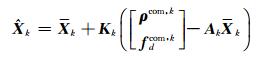
|
(13) |
式中, ρcom, k、fdcom, k分别为k历元GPS/BDS伪距与多普勒向量。k时刻状态参数的协方差矩阵为:
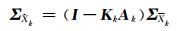
|
(14) |
在城市稠密地区, 多路径误差为主要误差源。为了抑制多路径误差的影响, 根据抗差自适应理论, 对观测向量权矩阵进行选权迭代, 构造等价权Pk; 根据状态不符值统计量, 构造自适应因子αk, 即得到抗差自适应滤波解[8-12]:
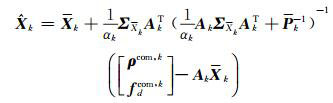
|
(15) |
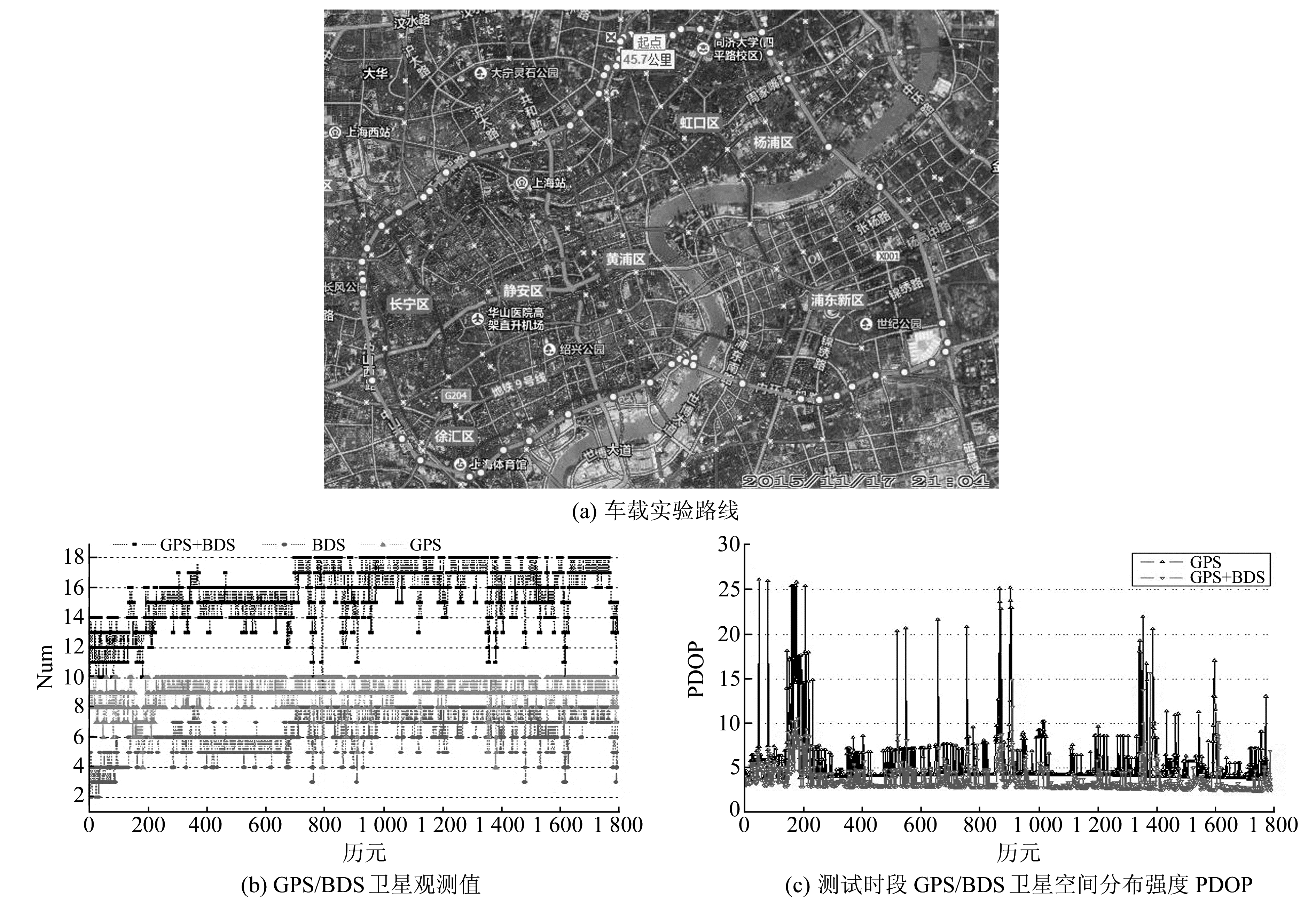
本文利用GPS/BDS双模接收机在上海城区进行车载实验, 车上同时安置了一台高精度GNSS RTK接收机。实验路线为一个闭合环路(图 1(a)), 有的路段较开阔, 卫星接收条件好; 有的路段有高楼及挡板, 卫星接收条件差。数据采样间隔为1 s, 测试时段大约30 min、1 800个历元。由图 1(b)可知, 整体上GPS卫星观测数比BDS卫星数要多, 开阔路段GPS卫星数为9颗左右, BDS卫星数为6颗左右; 在个别路段, 由于受高楼阻挡, GPS卫星数只有4颗, 而BDS卫星数有时只有2颗。当采用GPS+BDS组合时, 卫星观测数总体上可以保持在10颗以上。图 1(c)为采用GPS和GPS+BDS时的卫星几何强度因子。可以看出, 当采用GPS单系统时, 在很多路段其PDOP还是出现了大于10的情况, 当采用GPS+BDS组合系统时, 其PDOP得到了明显的改善, 只有少部分点大于10。
|
图 1 车载测试区域和卫星接收情况 Fig. 1 The vehicle test area and observed satellite information |
为了分析比较不同定位算法的效果, 分别采用以下3种方案对车载测试数据进行处理:1)GPS伪距单点定位; 2)GPS/BDS双系统伪距单点定位; 3)本文算法, 即基于GPS/BDS伪距多普勒观测值的抗差自适应滤波算法(方案1和方案2解算时, 也采用抗差滤波方法)。
分析时采用实时RTK的解算结果作为真值进行比较, 没有RTK结果的不纳入精度统计。解算时, 滤波初值由单点定位给出, 动态模型的协方差矩阵按式(16)给定:
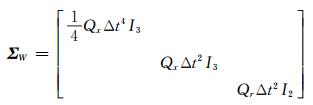
|
(16) |
式中, Qx=0.1, Qr=1 000。
对于伪距与多普勒的权重, 根据接收板的实验统计结果, 取二者权比为10。3种方案的定位结果平面坐标分量误差分别见图 2~4, 平面点位误差统计及其与方案1的比较结果见表 1。
|
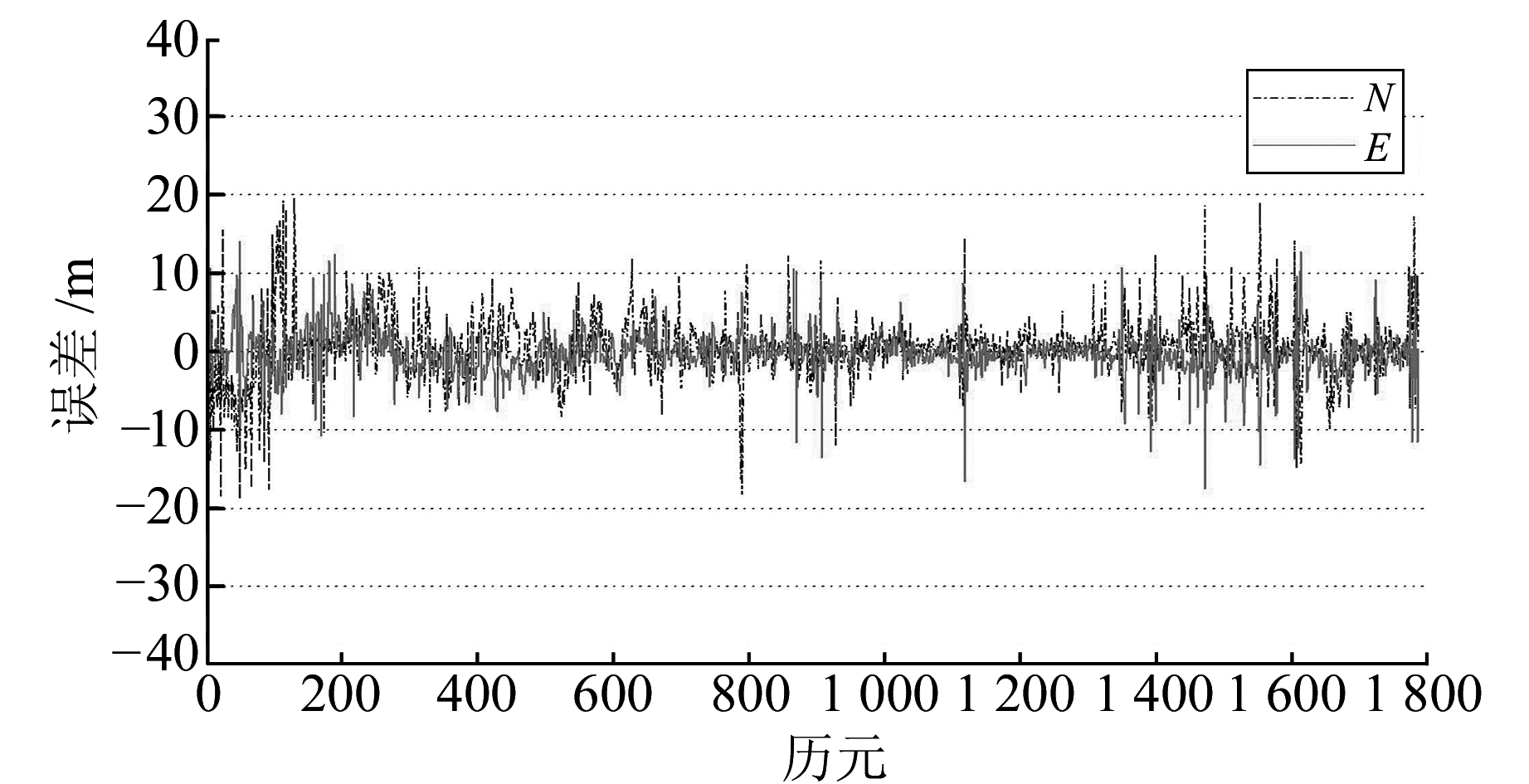
图 2 GPS单点伪距点定位误差(方案1) Fig. 2 Results of GPS SPP |

|
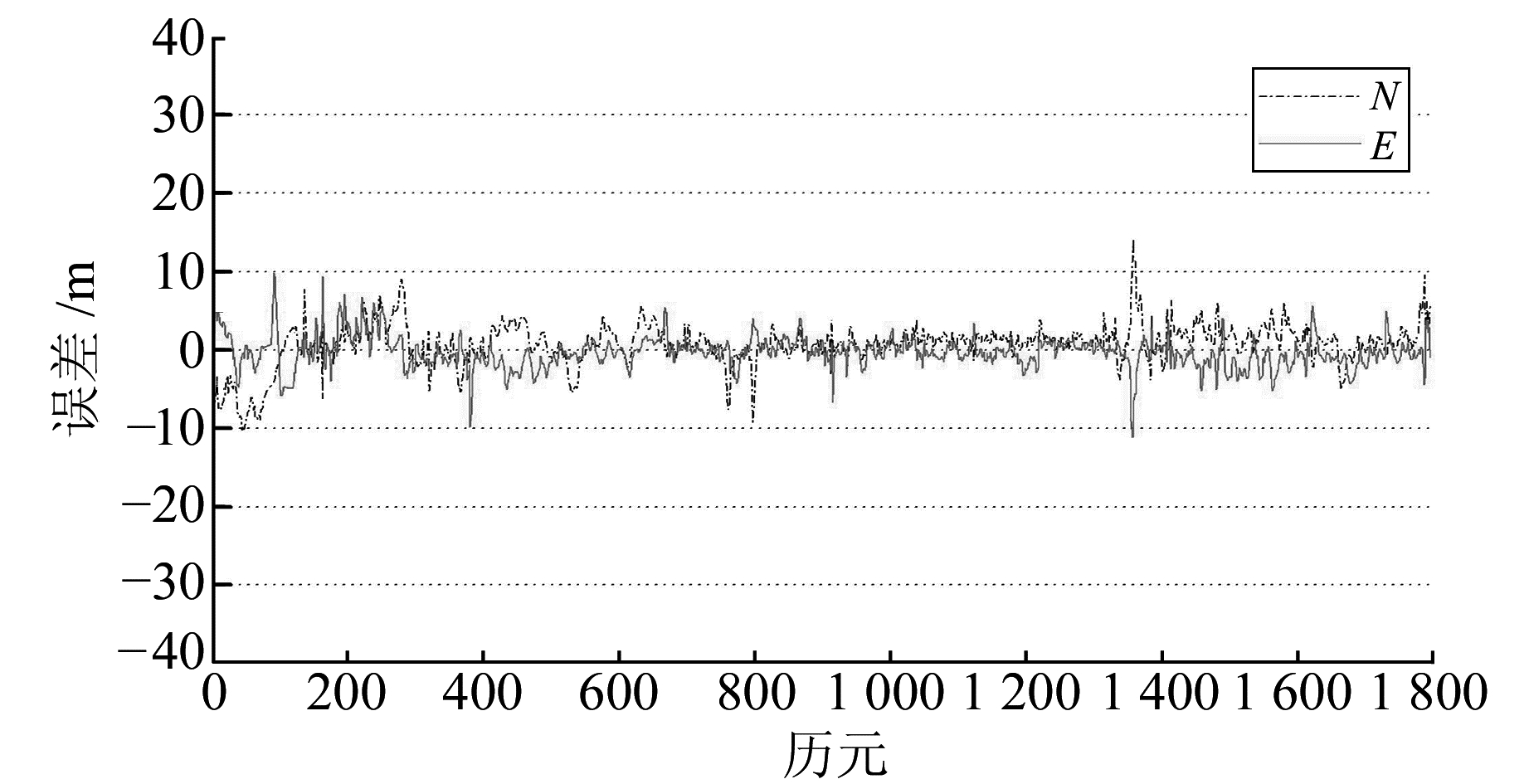
图 3 GPS/BDS组合伪距点定位误差(方案2) Fig. 3 Results of GPS/BDS SPP |
|
图 4 GPS/BDS伪距多普勒抗差自适应定位误差(方案3) Fig. 4 Results of GPS/BDS robust adaptive Kalman filter |
|
|
表 1 3种方案的平面点位精度(RMS)统计 Tab. 1 Statistics of horizontal position error |
从图 2和图 3可以看出, 加入北斗观测数据后, 定位精度获得了改善, 由4.9 m提高至4.3 m, 提高了12%(表 1)。由图 4可以看出, 采用本文算法后, 结果明显优于图 2和图 3, 特别是一些大的误差跳变(历元800、1 100、1 800)得到改善, 整体效果更平滑。与方案1相比, 点位精度提高了30%;与方案2相比, 点位精度提高了20%, 验证了本文算法的有效性。
为进一步比较方案2和方案3的定位效果, 绘制800历元附近的局部放大定位结果轨迹图(图 5)。从图 5可以看出, 此路段高楼林立, 容易造成多路径误差, 采用伪距单点定位其结果产生了较大跳跃, 采用本文算法定位结果则基本保持了行车轨迹的平滑性, 定位精度得到明显改善。

|
图 5 800历元附近动态定位轨迹 Fig. 5 The car trajectory around epoch 800 (圆标志为RTK; 针标志为方案2;五角标志为方案3) |
1) 在城市稠密地区进行卫星导航定位, 相比于GPS单系统, GPS/BDS组合能提高定位有效性和精度。
2) 城市环境中伪距观测值容易受到多路径误差的影响, 降低定位精度, 采用伪距多普勒联合的抗差自适应定位算法能够有效抑制粗差, 平滑导航定位结果, 提高卫星导航定位的精度。
3) 车载导航实验结果显示, 与GPS单系统伪距定位相比, 采用GPS/BDS伪距点定位, 点位精度由4.9 m提高到4.3 m; 采用本文算法, 点位精度由4.3 m进一步提高到3.4 m。
| [1] |
杨元喜. 自适应动态导航定位[M]. 北京: 测绘出版社, 2006 (Yang Yuanxi. Adaptive Navigation and Kinematic Positioning[M]. Beijing: Surveying and Mapping Press, 2006)
(  0) 0) |
| [2] |
杨元喜, 何海波, 徐天河. 论动态自适应滤波[J]. 测绘学报, 2001, 30(4): 293-298 (Yang Yuanxi, He Haibo, Xu Tianhe. Adaptive Robust Filtering for Kinematic GPS Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(4): 293-298 DOI:10.3321/j.issn:1001-1595.2001.04.004)
(  0) 0) |
| [3] |
Meyerhoff S L, Evans A G.Demonstration of the Combined Use of GPS Pseudorange and Doppler Measurements for Improved Dynamic Positioning[C].International Symposium on Marine Positioning, Netherlands, 1987
(  0) 0) |
| [4] |
刘大杰, 施一民, 过静珺. 全球定位系统的原理与数据处理[M]. 上海: 同济大学出版社, 1996 (Liu Dajie, Shi Yimin, Guo Jingjun. Principle and Data Processing of GPS[M]. Shanghai: Tongji University Press, 1996)
(  0) 0) |
| [5] |
Lei D Y, Lu W J, Yu D S.Doppler-Aided Algorithm for Beidou Position[C].China Satellite Navigation Conference, Wuhan, 2013
(  0) 0) |
| [6] |
Li L Y, Zhong J, Zhao M J. Doppler-Aided GNSS Position Estimation with Weighted Least Squares[J]. IEEE Transactions on Vehicular Technology, 2011, 60(8): 3 615-3 624 DOI:10.1109/TVT.2011.2163738
(  0) 0) |
| [7] |
杨元喜, 徐天河. 基于移动开窗法协方差估计和方差估计的自适应滤波[J]. 武汉大学学报:信息科学版, 2003, 28(6): 714-718 (Yang Yuanxi, Xu Tianhe. An Adaptive Kalman Filter Combining Variance Component Estimation with Covariance Matrix Estimation Based on Moving Window[J]. Geomatics and Information Science of Wuhan University, 2003, 28(6): 714-718)
(  0) 0) |
| [8] |
杨元喜. 抗差估计理论及其应用[M]. 北京: 八一出版社, 1993 (Yang Yuanxi. Robust Estimation Theory and Its Application[M]. Beijing: Bayi Press, 1993)
(  0) 0) |
| [9] |
Huber P J. Breakthroughs in Statistics[M]. New York: Springer, 1992
(  0) 0) |
| [10] |
Yang Y X, He H B, Xu G C. A New Adaptively Robust Filtering for Kinematic Geodetic Positioning[J]. Journal of Geodesy, 2001, 75(2-3): 109-116 DOI:10.1007/s001900000157
(  0) 0) |
| [11] |
Bancroft S. An Algebraic Solution of the GPS Equations[J]. IEEE Transactions on Aerospace and Electronic Systems, 1985(1): 56-59
(  0) 0) |
| [12] |
张双成, 杨元喜, 张勤, 等. 一种基于Bancroft算法的GPS动态抗差自适应滤波[J]. 武汉大学学报:信息科学版, 2007, 32(4): 309-311 (Zhang Shuangcheng, Yang Yuanxi, Zhang Qin, et al. An Adaptively Robust Filter Based on Bancroft Algorithm in GPS Navigation[J]. Geomatics and Information Science of Wuhan University, 2007, 32(4): 309-311)
(  0) 0) |
2. College of Surveying and Geo-Informatics, Tongji University, 1239 Siping Road, Shanghai 200092, China;
3. College of Geomatics and Geoinformation, Guilin University of Technology, 319 Yanshan Street, Guilin 541006, China
 2017, Vol. 37
2017, Vol. 37


