2. 73141部队, 南安市, 362302;
3. 71217部队, 莱阳市, 265200
ITRF2014是继ITRF2008后的新一代地球参考框架, 由国际地球自转与参考系统服务(IERS)维持与定期更新。随着空间大地测量技术的进步、实测数据的更新与积累以及数据处理策略的改进, ITRF2014相比于ITRF2008在数据数量与质量、参数模型的建立、测站全球分布的合理性等方面都有提高。用于建立ITRF2014的空间大地测量技术包括SLR(卫星激光测距)、VLBI(甚长基线干涉)、DORIS(多普勒定轨无线电综合定位)、GPS(全球定位系统)[1]。用于计算ITRF2014的ITRS分析中心分别为IGN(巴黎)、DGFI-TUM(慕尼黑)、JPL(帕萨迪纳)。ITRF2014在历元2010.0下, 给出了台站的坐标、速度以及EOPs(地球定向参数)。从2015-02开始, 所有技术(SLR、VLBI、GPS、DORIS)的输入数据都已经可以下载[2]。
ITRF2014是对SLR、VLBI、DORIS、GPS四种空间大地测量技术在各个年份的观测数据进行重新整合计算而得出的精细参考框架, 由以下框架参数定义[1-2]:
1) 坐标原点:仅由SLR数据确定。在历元2010.0下, ITRF2014坐标原点相对于ILRS和SLR长期解的平移与平移变化率为0。
2) 尺度:由SLR与VLBI联合确定。在历元2010.0下, 相对于VLBI和SLR的尺度与尺度变化率为0。
3) 定向:遵循地壳整体无旋转条件。在历元2010.0下, ITRF2014相对于ITRF2008的旋转参数与旋转速率为0。
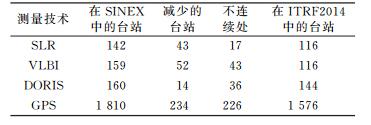
1 ITRF输入数据ITRF2014的输入数据为ILRS(国际激光测距服务)、IDS(国际DORIS服务)和IGS(国际全球导航卫星服务)提供的卫星测量技术的周解, 以及IVS(国际VLBI服务)提供的日解、站坐标和EOPs。4项技术的输入数据基本情况如表 1所示。
|
|
表 1 ITRF2014所用的空间大地测量技术解的情况[2] Tab. 1 The situation of space geodetic technique solutions used in ITRF2014[2] |
此外, 各个并置站之间的连接数据与大气载荷数据也作为ITRF2014的输入数据。其中并置站的局部连接数据由并置站、IGN测量部门和Altamimi收集并提供, 格式为SINEX; ITRF2014的大气载荷数据由IERS的GGFC与基于NCEP的模型提供, 为自由格式[2]。
在ITRF2014中, 来自SINEX文件的输入数据相对于ITRF2008也有了部分提升[2]。
1) VLBI:使用无约束的法方程组与完整的统计资料。
2) SLR:使用松弛约束的法方程组与完整的统计资料。
3) GPS:关于原点与定向的最小约束法方程组, 只建立了每日的尺度参数, 无完整统计资料, 需进行粗略估计。
4) DORIS:使用最小约束法方程组, 此约束不包含在SINEX文件中, 因此, 原点、尺度、定向需要在每周的法方程组中建立参数, 使用完整统计资料。
2 ITRF2014站分布ITRF2014增加了最近6 a的观测数据和新的测站, 减少了部分数据质量较差与分布不合理的测站。GPS技术在ITRF2014测站网点中占主导地位, 其比例从ITRF2008的60%升至ITRF2014的80%, 其中450个GPS测站是在2007年以后安装运行的[3]。此外, 新的星载DORIS接收机的使用增加了可用卫星数据, 因此台站有了更好的全球分布(图 1)。表 2为ITRF2014站点数目的基本情况。
3 ITRF2014数据分析策略 3.1 ITRF2014数据分析步骤
综合ITRF2014时采用与ITRF2008相同的分析战略, 分为如下步骤:
1) 处理SLR技术周解的过程中, 对所有松弛约束采用最小约束的方法。
2) 对以法方程组形式给出的IVS解集中, 施加无绝对平移和整体无旋转条件。
3) 处理IGS与IDS的周解过程中, 采用最小约束法。
4) 对每个技术长期解的估计过程中, 采用叠加单个技术时间序列的方法, 给出包括台站位置、速度、EOP日解以及每个技术的7个转换参数的周解或日解。另外, 在时间序列的叠加过程中, 在足够的时间跨度下, 给出台站1 a期与半年期的预测信号, 在建立时间序列的叠加法方程组之前, 给出震后形变模型(PSD)进行修正, 并应用于地震台站。
5) 识别与剔除异常值, 对地震台站的不连续处采用分段线性函数法与给出的PSD模型进行处理。
6) 考虑并置站之间的联系, 并且适当赋予局部联系一定的权重, 维持ITRF2014与单个技术解之间的一致性。
7) 产生ITRF2014的解, 包括台站位置坐标、速度以及EOPs参数。VLBI与SLR从80年代早期就开始提供EOPs参数, DORIS从1993年开始提供, GPS从1994年开始提供。
此种策略相对于参数组合法的优点为[4]:1)在联合处理之前, 不需要对大地基准进行约束处理; 2)在联合处理过程中不需要进行相似变换。
图 2为ITRF2014数据处理的流程。
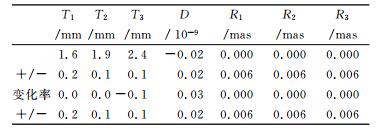
3.2 各技术解与综合解精度各技术解的内部精度由加权均方根WRMS来评价。在基准参数中, 4个技术转换参数的站心坐标系(E、N、U)分量的WRMS分别为:SLR:3.7 mm、3.6 mm、6.6 mm; VLBI:1.9 mm、2.3 mm、3.5 mm; GPS:1.6 mm、1.9 mm、2.4 mm; DORIS:9.1 mm、7.1 mm、8.0 mm。在2005.0历元下, 综合ITRF2014分析结果, 技术尺度与尺度变化率的误差分别为:SLR:0.01 mm/a; VLBI:0.01 mm、0.002 mm/a; DORIS:0.029 mm/a。
与ITRF2008类似, ITRF2014提供极移与其变化率、世界时(UT1-UTC)、日长(LOD)与章动。不同的是, 在ITRF2008中, LOD由VLBI技术唯一确定; 而在ITRF2014中, LOD由VLBI与GPS两种技术联合确定。在ITRF2014中, VLBI技术还单独提供了章动偏移量[2]。
在对ITRF2014的解的研究中, 有两个方面的问题需要注意:
1) 尺度误差。根据之前IVS提供的时间序列, VLBI技术的尺度误差应稳定在0.1 mm; 但根据ITRF2014发现, 现在的尺度误差高达-1.2 mm, 产生这种现象的原因有待进一步研究[4]。
2) 一致性。ITRF2014与ITRF2008的转换参数有很好的一致性, 并且随着解算模型的变化, 尺度上没有大变化; 但是在VLBI与SLR确定尺度参数的一致性方面还有待商榷。
4 ITRF2014与ITRF2008的比较 4.1 模型的改进对全球测站的非线性运动进行模型化处理, 并对其中的季节性周期项(如1 a期或者半年期)进行估计。在已经公布的12个版本的ITRF中, ITRF2014首次考虑了非潮汐大气载荷[2]。
4.2 新产品的推出1) 震后形变模型(能在任一历元下传递参数)[2]。现在已经发布的有:用于ITRF2014的完整的参数模型方程组、以SINEX文件形式发布的震后形变模型预测参数与方差。同时, 震后形变模型以测站振幅的时间函数形式给出。
测站位置坐标用XPSD表示, 历元用t表示, 初始历元用t0表示, 则测站位置坐标表示为[5]:
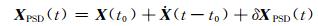
|
(1) |
式中, 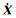
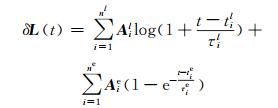
|
(2) |
式中, nl与ne分别表示模型中的对数项项数与指数项项数, Ail与Aie分别表示ith对数项与指数项的振幅, τil与τie分别表示ith对数项与指数项的阻尼时间, til与tie分别表示对应于ith对数项与指数项的地震时间, δL(t)的方差可记为:
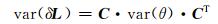
|
(3) |
式中, θ是震后形变模型的参数矢量, 矩阵C由δL(t)对模型中(对数项与指数项)振幅的偏导数、对阻尼时间的偏导数组成。
震后模型确定后, 能独立地提供每个测站的NEU坐标, 并且在每个测站坐标向量之间不会有交叉干扰项(或改正)。但是在方程的方差计算过程中, 需考虑每个振幅与阻尼时间(对数项和指数项)之间的交叉干扰项。
2) 只基于SLR技术的地心运动模型。为了提升地心运动观测质量, 可以在原有激光动力学卫星(LAGEO)观测的基础之上, 增加地球低轨卫星(LEO)进行联合观测。与之前仅依靠LAGEO卫星进行地心观测的策略相比, 虽然提升了地心运动的观测质量, 但是由于低轨卫星的模型误差影响地心运动的计算精度, 并且GPS与DORIS技术对地心运动的解在抗模型误差方面较为薄弱[2], 因此在ITRF2014的地心运动建模中, 最好只运用SLR技术。但是由于SLR测站全球分布不合理的情况在短期内难以改变, 因此需要通过对SLR确定地心的算法与模型进行更好地优化、提升LAGEO卫星的硬件质量等方法来进行SLR地心运动建模。
5 ITRF2014与ITRF2008之间的转换参数与ITRF2014的解 5.1 ITRF2014与ITRF2008之间的转换参数ITRF2014到ITRF2008的转换参数是由127个测站(坐落于125个站点)进行观测计算得出的, 转换参数与速率如表 3所示。用于测量计算ITRF2014与ITRF2008之间转换参数的站点(包括89个GPS站、24个VIBL测站、8个SLR测站和2个DORIS测站)如图 3所示。
|
|
表 3 在历元2010.0下ITRF2014与ITRF008之间的转换参数 Tab. 3 The transformation parameters between ITRF2014 and ITRF2008 |
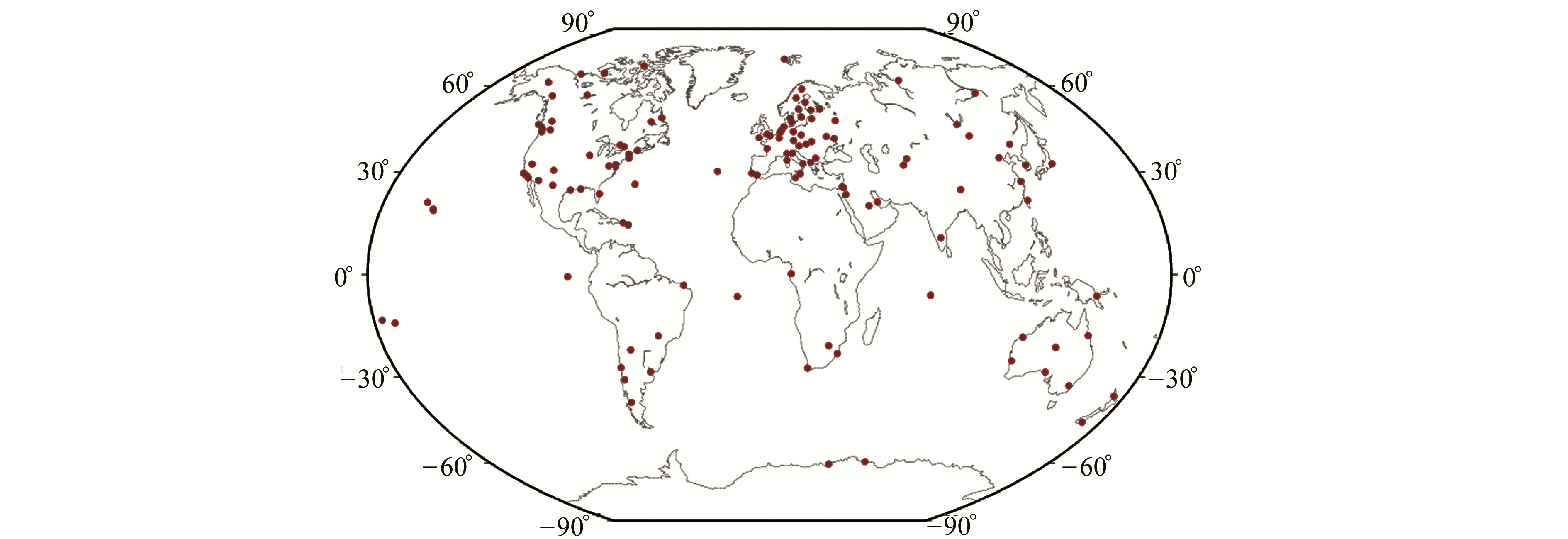
|
图 3 计算转换参数的站点 Fig. 3 The sites using for calculating the transformation parameters |
ITRF2014的解的结果包括地心运动与尺度的时间序列文件、测站位置残差序列文件以及结果文件。前两种文件在ITRF网站上已经公布, 可查到具体测站的序列图像; 结果文件以SINEX格式给出, 包括测站位置文件、速率残差文件和解文件。解文件又包括整体平差的解文件和各种技术的解文件, 其中包含全部参数的方差-协方差矩阵, 以及从初始历元以来的测站位置、速率和EOPs。现在新公布了每种技术的震后形变模型参数文件, 使用CATREF国际格式。
6 结语ITRF2014在ITRF2008的基础上优化了全球台站分布和框架改正模型; 首次考虑了非潮汐大气载荷模型, 提升了参考架精度; 提出了地心运动模型与震后形变模型, 其中新建立的震后形变模型为地震预测与板块运动监测提供了保障, 能在短期内通过扣除震后形变模型值校准测站坐标, 为研究全球地壳形变(特别是多震、强震地区局部形变)提供强大的支持, 也为进一步研究全球测站非线性变化的区域性规律打下了基础, 有利于建立更高精度的地球参考框架。
| [1] |
成英燕. ITRF2008框架简介[J]. 大地测量与地球动力学, 2012, 32(1): 47-50 (Cheng Yingyan. The Introduction of ITRF2008[J]. Journal of Geodesy and Geodynamics, 2012, 32(1): 47-50)
(  0) 0) |
| [2] |
Seitz M, Angermann D, Blossfeld M, et al.2014 ITRS Realization of DGFI: DTRF2014[C].EGU General Assembly Conference, Vienna, 2015
(  0) 0) |
| [3] |
Spatar C B, Moore P, Clarke P J, et al. Collinearity Assessment of Geocentre Coordinates Derived from Multi-Satellite SLR Data[J]. J Geod, 2015, 89(12): 1 197-1 216 DOI:10.1007/s00190-015-0845-x
(  0) 0) |
| [4] |
Tornatore V, Kayikçi E T, Roggero M.Analysis of GPS, VLBI and DORIS Input Time Series for ITRF2014[R].European VLBI Group for Geodesy and Astrometry Working Meeting, Ponta Delgada, Azores, 2015
(  0) 0) |
| [5] |
Altamimi Z, Rebischung P, Métivier L, et al.Status of ITRF2014 Analysis Work is Still in Progress[R].EUREF Symposium, Leipzig, 2015
(  0) 0) |
2. PLA 73141 Troops, Nan'an 362302, China;
3. PLA 71217 Troops, Laiyang 265200, China
 2017, Vol. 37
2017, Vol. 37