2. 武汉大学测绘学院, 武汉市珞喻路129号, 430079;
3. 宿迁学院建筑工程学院, 宿迁市黄河南路399号, 223800
在测量工作中, 坐标转换不可避免。处理坐标数据时, 常面对超定方程式Ax = b的病态问题[1-4]。病态方程系数阵A的条件数很大, 当系数阵A或向量b存在细微扰动时, 解向量x会远离真实解[5]。陈宇等[6]的研究表明, 在100 km× 100 km测区范围的工程应用中, 由于布尔莎模型解得的平移参数与旋转、尺度参数之间存在很强的相关性, 解算模型呈病态。以往关于空间直角坐标转换模型病态问题的研究多集中于小旋转角情形[7-10], 但在工程测量坐标系间的转换和摄影测量空间坐标系间的转换中, 大角度的情形普遍存在。大旋转角的空间直角坐标转换需解决非线性的问题, 对模型线性化后基于最小二乘迭代求解是常用的处理方法[11-14], 但该情形下的病态问题研究较少。
本文在分析大旋转角空间直角坐标转换模型病态性的基础上, 提出坐标中心化与自适应缩放相结合的空间直角坐标转换改进模型, 并结合算例验证改进模型的有效性和可靠性。
1 空间直角坐标转换通用模型空间直角坐标转换模型为:
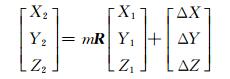
|
(1) |
式中, [Xj, Yj, Zj]为坐标系(j=1, 2)下的坐标, [ΔX, ΔY, ΔZ]T为平移参数, m为尺度参数, R为旋转矩阵:
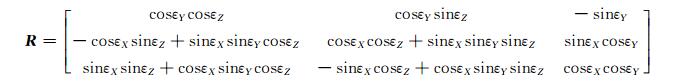
|
其中, εX、εY、εZ为空间直角坐标变换的3个旋转角。
将式(1)在近似值(ΔX0, ΔY0, ΔZ0, R0, m0)处以泰勒级数展开:

|
(2) |
式中, 目标坐标[X2, Y2, Z2]的近似值[(X), (Y), (Z)]表示为:
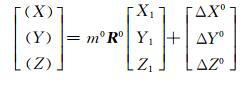
|
(3) |
式中, ΔX0、ΔY0、ΔZ0、R0、m0分别为3个平移参数的近似值、旋转矩阵的近似值和尺度参数的近似值。
由式(2)可列误差方程:
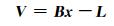
|
(4) |
式中, x为参数向量改正值, x =[dΔX dΔY dΔZ dεX dεY dεZ dm]T, L为观测向量, L =[X2 Y2 Z2]T-[(X) (Y) (Z)]T, V为观测值误差向量, B为系数阵:

|
其中, ∂(X2, Y2, Z2)/∂εX、∂(X2, Y2, Z2)/∂εY、∂(X2, Y2, Z2)/∂εZ和∂(X2, Y2, Z2)/∂m分别为坐标值对3个旋转角、1个尺度参数的偏导数。
在大旋转角空间直角坐标转换模型求解时, 首先确定转换参数的初始值, 构造误差方程式。然后根据最小二乘原理, 求解参数向量改正值x。最后检验x是否小于阈值, 若小于阈值, 则退出迭代; 否则利用上一次所得近似值, 加上本次迭代的x, 作为新的转换参数近似值, 重新计算x的新值, 直至符合要求。
观测向量误差对解向量误差的影响与法方程系数阵的条件数成正比, 当条件数很大时, 会造成转换模型病态。良态模型可保证稍有扰动时问题的解接近无扰动时的解, 病态模型会对良性问题给出差的解。在实际工程中, 坐标原点往往在测区外或公共点集中于一个局部范围内, 这使得法方程系数矩阵主对角线不占优, 其条件数‖ BTB ‖22‖(BTB)-1‖22很大, 导致解向量抗扰动能力弱。
2 改进的空间直角坐标转换模型将原始坐标系和目标坐标系中的坐标分别中心化, 使坐标点均匀分布在整个空间坐标系中, 此时法方程系数阵主对角线占优, 故其条件数较小。若测区内有n个公共点, 设[Xj, Yj, Zj]i为坐标系j(j=1, 2)下的第i点坐标, 则测区中心点坐标为:
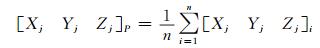
|
(5) |
中心化后的坐标[X′j Y′j Z′j]为:
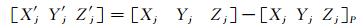
|
(6) |
为公式推导及计算方便, 令
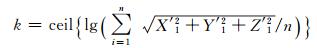
|
(7) |
为进一步改善法方程系数阵的结构, 还需对误差方程系数阵B中的部分元素自适应地施加缩放因子ρ′、d′, 即在X′2、Y′2、Z′2的基础上, 使得
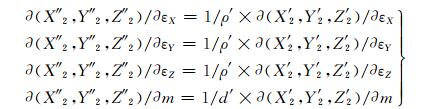
|
(8) |
式中, ρ′=180/π×3 600×10k-5, d′=10k, ∂(X′2, Y′2, Z′2)/∂εX、∂(X′2, Y′2, Z′2)/∂εY、∂(X′2, Y′2, Z′2)/∂εZ和∂(X′2, Y′2, Z′2)/∂m分别为用[X′1, Y′1, Z′1]替代式(4)系数阵B中的[X1, Y1, Z1]。
k的取值根据式(7)自适应求得, 假设测区范围为100 m×100 m左右, 中心化后的坐标[X′ j, Y′ j, Z′j]、缩放因子d′和ρ′均为102量级。若k的取值过小或过大, 则法方程系数阵主对角线元素仍不占优, 矩阵呈病态。用经过中心化的坐标与自适应缩放处理后的X″2、Y″2、Z″2代替X2、Y2、Z2, 以X′1、Y′1、Z′1代替X1、Y1、Z1, 即为改进的空间直角坐标转换模型。改进的转换模型显著改善了法方程系数阵的结构, 所得转换参数的抗扰动能力强。
按最小二乘原理, 利用3个或3个以上公共控制点, 可迭代解算大旋转角空间直角坐标转换模型的7个转换参数。计算过程如下:
1) 首先确定未知参数初始近似值, 即ΔX0=0、ΔY0=0、ΔZ0=0、εX0=0°、εY0=0°、εZ0=0°、m0=1;
2) 对两套坐标系下的公共控制点坐标分别中心化;
3) 由转换参数近似值和中心化后的坐标值, 经式(4)得误差方程系数矩阵B和观测向量L, 组成误差方程;
4) 根据最小二乘原理构造法方程;
5) 解算法方程, 求得参数向量的改正值x;
6) 将本次得到的x与阈值比较, 若小于阈值, 则迭代结束, 否则用前一次迭代得到的转换参数近似值, 加本次迭代的x, 作为新的转换参数近似值, 重复步骤3)~5), 直到获得满足要求的转换参数估值。
3 算例分析在下述算例分析中, 参照其他坐标转换模型迭代终止的条件, 将平移参数、旋转参数和尺度参数的限差分别控制在1 mm、10-3 s和10-7以内。
选取某地区8个控制点的空间直角坐标作为原始坐标, 为便于分析, 假设观测误差具有独立性和等方向性。模拟一套大旋转角坐标转换参数, 由式(1)计算目标坐标并分别加中误差为5 mm的随机误差作为目标坐标测量值。原始坐标和目标坐标测量值如表 1所示。
|
|
表 1 原始坐标和目标坐标 Tab. 1 The original coordinates and the target coordinates |
选择1~5号点作为公共点, 并以其坐标均值作为测区中心点坐标, 其余3个点作为检核点。分别采用现有空间直角坐标转换模型和本文改进模型, 通过等权平差解算坐标转换参数, 分析模型的病态性、转换参数的抗扰动性和转换精度。
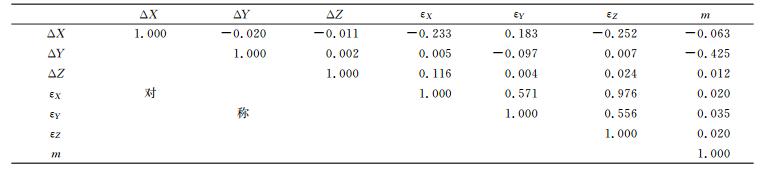
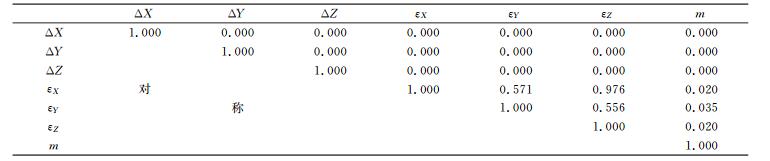
3.1 转换模型的病态性从表 2可以看出, 现有模型7个参数之间存在很强的相关性。表 3表明, 改进模型仅旋转参数、尺度参数之间存在相关性。
|
|
表 2 现有模型转换参数的相关性 Tab. 2 Correlativity among the traditional model transformation parameters |
|
|
表 3 改进模型转换参数的相关性 Tab. 3 Correlativity among the improved model transformation parameters |
计算得出, 现有模型和改进模型的法方程系数阵的条件数分别为1.3×107和85.73。现有模型条件数很大, 模型病态; 而改进模型的条件数小于1 000, 模型不病态[15], 改进模型远优于现有模型。模型呈病态时, 求解参数间存在显著相关性。对于工程测量而言, 实际控制点难以均匀分布, 且坐标原点往往不在测区中央, 造成构造的设计矩阵存在复共线性, 故平移参数与其余参数存在很强的相关性。改进模型中, 测区内坐标经过中心化, 另对误差方程系数阵施加自适应缩放因子, 削弱了控制点坐标数值上的相关性, 使得旋转参数与尺度参数对坐标转换的影响变大, 平移参数与其他参数不再相关。
3.2 转换参数的抗扰动性为比较现有模型与改进模型解算结果的抗扰动性, 对目标坐标系引入扰动。以1号点含有扰动为例, 将目标坐标系中1号点的坐标X方向增加1 cm、Y方向增加1.5 cm、Z方向减少1.2 cm, 其他点的坐标不改动。对引入扰动前、后的坐标分别利用两种模型解算转换参数, 结果如表 4所示。
|
|
表 4 两种情形的转换参数及精度 Tab. 4 Transformation parameters and precision in both cases |
从表 4可以看出, 改进模型经过中心化, 与现有模型的平移参数值有较大差异, 改进模型算得的平移参数精度较高; 现有模型的旋转参数与改进模型的旋转参数结果一致, 精度相同。由于实际工程中尺度参数很少改变, 本算例亦未考虑尺度变化, 故表 4未列出尺度参数。
比较表 4中引入扰动前、后两种模型的参数解算结果可知, 坐标的细小变化对现有模型的平移参数及其中误差产生了较大影响, 而对改进模型的平移参数没有影响, 对其中误差影响亦较小。虽然观测值的扰动对旋转参数的影响可以忽略, 但导致其精度降低至秒级。所以, 现有模型算得的转换参数抗扰动性低于改进模型, 且扰动越大, 差别越明显。
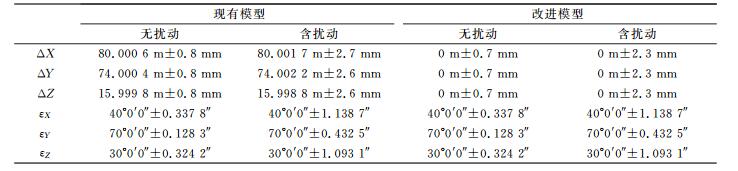
3.3 坐标转换精度分别利用引入扰动前、后两种模型算得的转换参数求解所有点在目标坐标系中的转换坐标。经比较, 无扰动时两种模型的转换坐标及其中误差相同; 含扰动时两种模型亦相同, 但改进模型收敛速度更快。为便于评估模型的稳定性, 本文仍将变化后的1号点作为公共点, 引入扰动后的点位精度低于变化前。精度统计结果见表 5。
|
|
表 5 模型转换精度统计 Tab. 5 Statistics about model transformation accuracy |
虽然现有模型存在参数解相关性强、抗扰动性差的弊病, 但当公共点坐标确定时, 参数值仍是最优的, 在整体上不会对测区内转换点的转换结果产生影响。
4 结语1) 本文提出的测区坐标中心化和自适应缩放相结合的方法适用于大旋转角空间直角坐标的变换, 改善了法方程系数阵的结构, 提高了转换参数的精度。
2) 经实验数据及引入扰动数据验证, 改进模型的转换结果稳定可靠。
3) 本文提出的方法简化了计算数据, 易于编程实现, 具有很好的工程应用价值。
| [1] |
卢秀山. 病态系统分析理论及其在测量中的应用[M]. 北京: 测绘出版社, 2007 (Lu Xiushan. Pathological System Analysis Theory and Its Application in the Measurement[M]. Beijing: Surveying and Mapping Press, 2007)
(  0) 0) |
| [2] |
沈云中, 胡雷鸣, 李博峰. Bursa模型用于局部区域坐标变换的病态问题及其解法[J]. 测绘学报, 2006, 35(2): 95-98 (Shen Yunzhong, Hu Leiming, Li Bofeng. Ill Posed Problem in Determination of Coordinate Transformation Parameters with Small Areas Data Based on Bursa Model[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(2): 95-98 DOI:10.3321/j.issn:1001-1595.2006.02.001)
(  0) 0) |
| [3] |
郭建锋.测量平差系统病态性的诊断与处理[D].郑州: 信息工程大学, 2002 (Guo Jianfeng.Diagnostics and Processing of the Ill-Conditioning in Surveying Adjustment System[D].Zhengzhou: Information Engineering University, 2002)
(  0) 0) |
| [4] |
王解先. 七参数转换中参数之间的相关性[J]. 大地测量与地球动力学, 2007, 27(2): 43-46 (Wang Jiexian. Correlations among Parameters in Seven-Parameter Transformation Model[J]. Journal of Geodesy and Geodynamics, 2007, 27(2): 43-46)
(  0) 0) |
| [5] |
张贤达. 矩阵分析与应用[M]. 北京: 清华大学出版社, 2013 (Zhang Xianda. Matrix Analysis and Applications[M]. Beijing: Tsinghua University Press, 2013)
(  0) 0) |
| [6] |
陈宇, 白征东, 罗腾. 基于改进的布尔沙模型的坐标转换方法[J]. 大地测量与地球动力学, 2010, 30(3): 71-78 (Chen Yu, Bai Zhengdong, Luo Teng. An Improved Bursa Model for Coordinate Transformation[J]. Journal of Geodesy and Geodynamics, 2010, 30(3): 71-78)
(  0) 0) |
| [7] |
王解先, 王军, 陆彩萍. WGS-84与北京54坐标的转换问题[J]. 大地测量与地球动力学, 2003, 23(3): 70-73 (Wang Jiexian, Wang Jun, Lu Caiping. Problem of Coordinate Transformation between WGS-84 and Beijing 54[J]. Journal of Geodesy and Geodynamics, 2003, 23(3): 70-73)
(  0) 0) |
| [8] |
陈正宇, 刘春. 基于多参数正则化的空间坐标转换与精度分析[J]. 大地测量与地球动力学, 2008, 28(1): 92-95 (Chen Zhengyu, Liu Chun. Spatial Coordinate Transformation Based on Multiple Parameter Regularization and Its Accuracy Analysis[J]. Journal of Geodesy and Geodynamics, 2008, 28(1): 92-95)
(  0) 0) |
| [9] |
张华海, 王宝山, 赵长胜, 等. 应用大地测量学[M]. 徐州: 中国矿业大学出版社, 2011 (Zhang Huahai, Wang Baoshan, Zhao Changsheng, et al. Application of Geodesy[M]. Xuzhou: China University of Mining and Technology Press, 2011)
(  0) 0) |
| [10] |
孙小荣, 李明峰, 刘支亮. 平面四参数坐标转换模型的改进与应用研究[J]. 大地测量与地球动力学, 2015, 35(1): 132-135 (Sun Xiaorong, Li Mingfeng, Liu Zhiliang. Improvement and Application Study of Planar Four Parameters Coordinate Transformation Model[J]. Journal of Geodesy and Geodynamics, 2015, 35(1): 132-135)
(  0) 0) |
| [11] |
陈义, 沈云中, 刘大杰. 适用于大旋转角的三维基准转换的一种简便模型[J]. 武汉大学学报:信息科学版, 2004, 29(12): 1 101-1 105 (Chen Yi, Shen Yunzhong, Liu Dajie. A Simplified Model of Three Dimensional Datum Transformation Adapted to Big Rotation Angle[J]. Geomatics and Information Science of Wuhan University, 2004, 29(12): 1 101-1 105)
(  0) 0) |
| [12] |
姚宜斌, 黄承猛, 李程春, 等. 一种适用于大角度的三维坐标转换参数求解算法[J]. 武汉大学学报:信息科学版, 2012, 37(3): 253-256 (Yao Yibin, Huang Chengmeng, Li Chengchun, et al. A New Algorithm for Solution of Transformation Parameters of Big Rotation Angle's 3D Coordinate[J]. Geomatics and Information Science of Wuhan University, 2012, 37(3): 253-256)
(  0) 0) |
| [13] |
黄令勇, 吕志平, 任雅奇, 等. 多元总体最小二乘在三维坐标转换中的应用[J]. 武汉大学学报:信息科学版, 2014, 39(7): 793-798 (Huang Lingyong, Lü Zhiping, Ren Yaqi, et al. Application of Multivariate Total Least Square in Three-Dimensional Coordinate Transformation[J]. Geomatics and Information Science of Wuhan University, 2014, 39(7): 793-798)
(  0) 0) |
| [14] |
方兴, 曾文宪, 刘经南, 等. 三维坐标转换的通用整体最小二乘算法[J]. 测绘学报, 2014, 43(11): 1 139-1 143 (Fang Xing, Zeng Wenxian, Liu Jingnan, et al. A General Total Least Squares Algorithm for Three-Dimensional Coordinate Transformations[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(11): 1 139-1 143)
(  0) 0) |
| [15] |
孙志忠, 袁慰平, 闻震初. 数值分析[M]. 南京: 东南大学出版社, 2004 (Sun Zhizhong, Yuan Weiping, Wen Zhenchu. Numerical Analysis[M]. Nanjing: Southeast University Press, 2004)
(  0) 0) |
2. School of Geodesy and Geomatics, Wuhan University, 129 Luoyu Road, Wuhan 430079, China;
3. School of Civil Engineering and Architecture, Suqian College, 399 South-Huanghe Road, Suqian 223800, China
 2017, Vol. 37
2017, Vol. 37