GRACE卫星通过高精度星间微波测距观测值探测地球重力场的变化(仅通过重力感应,与地球无直接信号接触),可得到较高精度和较高时空分辨率的时变地球重力场模型[1-3]。但利用GRACE卫星实测数据解算的地球重力场模型精度与发射前的模拟精度仍然有差距,这种差距除受观测噪声、各向异性的空间采样、卫星重力反演方法影响外,大气与海洋去混频模型(也可称大气与海洋非潮汐高频质量变化模型或大气与海洋去混叠模型)的影响是不容忽视的因素。有必要深入研究大气与海洋去混频模型,提高去混频模型的精度[4-6]。
同时变地球重力场模型一样,大气与海洋去混频模型用截断到一定阶次的球谐位系数来表示,因此根据流体静力平衡原理,可将地球表面所受大气压力及海洋底部压力的变化转化为球谐位系数,这个过程通常采用球谐分析方法。球谐分析方法主要包括数值积分法和最小二乘法两类,数值积分法又包括常规梯形积分方法、去平滑积分方法、第一类Neumann积分(也称切比雪夫积分)和第二类Neumann积分(也称高斯-勒让德积分)[7-9]。不同的球谐分析方法需要利用不同形式的格网数据,计算的结果也不尽相同,但现有参考文献并未完整分析以上球谐分析方法对计算大气与海洋去混频模型的影响。GFZ公布的大气与海洋去混频模型产品(AOD1B RL05)采用的是常规梯形积分方法[10],而文献[4]采用第二类Neumann积分计算大气去混频模型,认为其在两极处相对于常规梯形积分具有更好的精度,但并未分析该方法相对于其他方法是否存在优越性。文献[11]采用考虑观测值误差的加权最小二乘方法计算大气与海洋去混频模型,该方法从理论上来说是最严密的,但大气与海洋模型都是采用同化技术获得,观测值误差很难准确获得,实际计算并未证明该方法具有较好的精度。
由以上可知,现有参考文献只利用了3种球谐分析方法进行大气与海洋去混频模型计算,且没有采用合适的衡量标准来比较出最优的球谐分析方法。基于此,本文以ERA-Interim表面大气压数据为例,导出了上述5种球谐分析方法计算大气去混频模型的公式,将计算得到的不同大气去混频模型应用于GRACE时变地球重力场模型的解算,并采用GRACE星间距离变率残差及时变地球重力场模型的精度来验证大气去混频模型的精度,从中优选出最适合于大气去混频模型计算的球谐分析方法。
1 球谐分析方法由表面大气压的变化转化为球谐位系数,可采用如下球谐分析公式[10-11]:

|
(1) |
式中,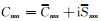
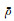
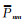

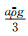
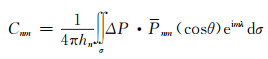
|
(2) |
由于ΔP的连续函数未知,因此其积分原函数无法计算,只能采集一定空间间隔的离散数据,用数值方法进行积分计算。当采用常规梯形积分进行计算时,式(2)可直接转化为:

|
(3) |
式中,N、M分别为纬线和经线条数(当起始经纬度都为0°时,对应格网数为N-1和M),格网面积Δσjk=Δλ(cosθj-cosθj+1)[9],Δλ为经度格网间隔。式(3)一般要求大气压为等角度规则格网分布,每一条纬线上的格网可采用快速傅里叶变换(FFT)计算,每一个格网内的大气压都采用ΔPjk近似代替,这种策略平滑了格网内的大气压变化。当采用格网内4个格网点平均值代替格网区域的值,并对格网内的区域进行解析积分时,加入去平滑参数,可得出一种去平滑积分方法:
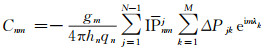
|
(4) |
式中,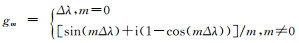
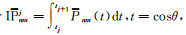
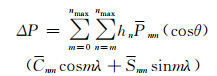
|
(5) |
式中,nmax为最大阶数。为了能利用FFT计算,上式对阶次的求和顺序进行了调换,并根据离散三角函数的正交性得:

|
(6) |
式中,
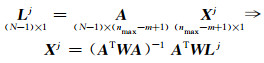
|
(7) |
式中,Lj为观测值向量,A为系数阵,Xj为未知参数向量,W为权阵。当j=0时,计算
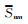
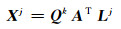
|
(8) |
式中,Qk=[q1k q2k … qN-1k]T,k=1代表第一类Neumann公式,k=2代表第二类Neumann公式,并有[8, 12]:

|
(9) |
式中,P′M/2(cosθp)表示非缔合Legendre函数的偏导数。要得到式(9)的权系数,第一类Neumann公式要求纬度间隔为经度间隔的一半(即Δφ=Δλ/2),第二类Neumann公式要求纬度格网为高斯格网分布(即要求PM/2(cosθp)=0)。
由以上可知,第一类和第二类Neumann公式都可由加权最小二乘原理设计特殊权阵严密推导出来,但这个权阵是人为设定的,并不是由观测值的误差信息推导出来的,而常规梯形积分和去平滑积分方法都只是近似数值积分方法。所以从公式推导来看,最小二乘法理论上最严密,其次是第一类和第二类Neumann方法,常规梯形积分和去平滑积分方法精度最低。这也可以由模拟数据计算验证(表 1)。
|
|
表 1 无误差数据的谱域及空域均方根 Tab. 1 RMS in spectral and spatial domain with error-free data |
由于GFZ采用ECMWF0.5°等间隔大气压数据计算100阶次大气去混频模型,在现有GRACE卫星观测值精度下并不需要考虑频谱泄漏效应,因此本文直接以AOD1B RL05的2007-01-01 00:00 100阶次大气去混频模型为例,将其作为“真实模型”,通过球谐综合得到0.5°×0.5°间隔的全球表面大气压数据。对于第一类Neumann公式,生成0.25°×0.5°间隔数据;对于第二类Neumann公式,生成N160高斯格网数据(即纬线条数为320条)。将球谐综合数据作为“真实格网数据”,再利用不同的球谐分析方法计算得到不同的大气去混频模型,最后由不同的大气去混频模型重新进行球谐综合得到全球表面大气压格网数据,构成闭循环过程。将计算模型与真实模型比较可得到谱域上的均方根(RMS),将计算格网数据与真实格网数据比较可得到空域上的均方根,计算结果如表 1所示,空域上的误差(计算值与真实值的差值)如图 1所示。
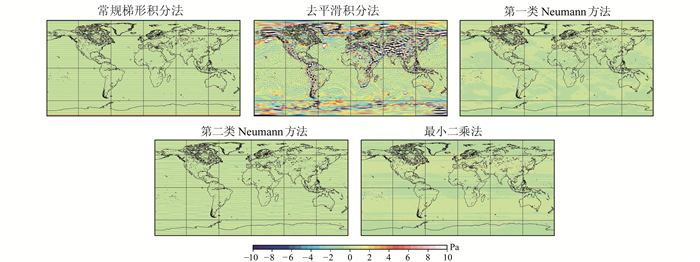
|
图 1 不同球谐分析方法的空域误差 Fig. 1 Errors in spatial domain with different spherical harmonic analysis methods |
从表 1和图 1可以看出,最小二乘法精度最高,其次是第一类和第二类Neumann方法;常规梯形积分方法在接近两极处误差较大,导致其整体精度偏低;去平滑积分方法采用块状平均值作为观测值,增大了无误差模拟观测值的误差,但其两极误差低于常规梯形积分法。因此整体上来说,去平滑积分方法与常规梯形积分方法精度相当。以上验证了理论上最小二乘法精度最高的结论。空域上最大均方根约为4 Pa,相当于0.4 mm的等效水高(1 hPa对应1 cm等效水高),能够满足GRACE卫星的精度要求。
以上是无误差的数据模拟,能够检验球谐分析方法的正确性。为了验证球谐分析方法的稳定性,对真实格网数据施加均值为0、中误差为50 Pa(占观测值百分比为0.05%~0.1%)的正态分布随机误差,再分别进行球谐分析和球谐综合,得到计算模型及计算格网数据。分别与真实模型和真实格网数据比较,结果如表 2及图 2所示。
|
|
表 2 含噪声数据的谱域及空域均方根 Tab. 2 RMS in spectral and spatial domain with white noise data |
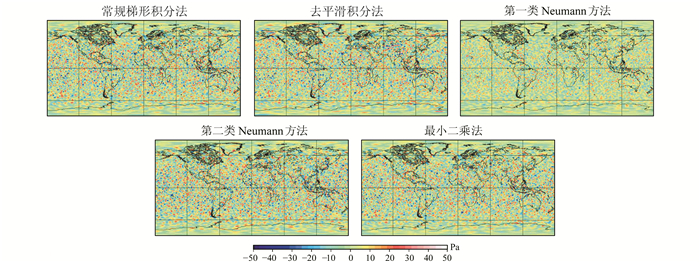
|
图 2 不同球谐分析方法的空域误差 Fig. 2 Errors in spatial domain with different spherical harmonic analysis methods |
可以看出,不同方法抵抗误差的能力不同。第一类Neumann方法精度最高,抵抗误差能力最强,其次是最小二乘方法;去平滑积分方法由于采用了块状平均值,能较好地平滑随机误差,其精度高于常规梯形积分方法和第二类Neumann方法。两类Neumann方法的本质都是通过设计权阵使得最小二乘的法方程矩阵为单位阵。由于选择的格网个数不同,导致设计的权阵不相等。第一类Neumann方法精度较高,可能是由于其格网个数普遍是其他方法的2倍,其抵抗误差的能力较强。第一类与第二类Neumann方法的空域均方根差值达到约4 Pa,相对于GRACE卫星的精度要求可以忽略不计,但对于GRACE-FO(follow-on)或NGGM(next generation gravity models)采用激光测距观测值的卫星重力任务要求,不同球谐分析方法的差距对探测时变重力场信号有一定影响。
3 实测数据计算以欧洲中程天气预报中心ECMWF的再分析大气模型ERA-Interim[13]的表面大气压为观测数据,采用2007年全年的平均大气压值,利用上述5种球谐分析方法,分别计算2007-01间隔6 h的100阶次5组大气去混频模型。从ERA-Interim获得的大气压数据为0.5°×0.5°等间隔数据,对于第一类和第二类Neumann方法,采用线性插值方法将原始数据内插为0.25°×0.5°间隔数据和N160高斯格网数据。对于最小二乘法,其权阵是根据观测数据的误差来确定的。将这5组大气去混频模型分别用于GRACE卫星重力反演,采用短弧长积分法[14-15],除大气去混频模型不一致以外,其他所有参考力模型及参数设置完全一致,计算5组60阶次的时变地球重力场模型及对应的星间距离变率残差。弧段长度设置为0.5 h,弧段局部参数包括边界轨道改正向量及加速度计偏差改正。参考力模型如表 3所示。
|
|
表 3 参考力模型 Tab. 3 Reference force models |
星间距离变率残差作为距离变率观测值与背景力模型拟合值的差距,若距离变率残差越小,说明大气去混频模型越接近真实情况,越能更好地移除大气质量的高频变化。为此,先对5种模型计算的星间距离变率残差进行分析,以常规梯形积分方法(GFZ采用)计算的星间距离变率残差为“参考值”,将其他4种方法计算的星间距离变率残差绝对值与“参考值”的绝对值相减,并投影到其星下点位置,可得到图 3的结果。若观测值与背景力模型拟合值的精度越高,则星间距离变率残差越小,因此星间距离变率残差的真实值应为0。若图 3中距离变率残差差值为负,说明该球谐分析模型越接近真实情况,优于常规梯形积分方法,反之则说明劣于常规梯形积分方法。可以看出,图 3中大部分差值为负值,尤其是高纬度地区,说明这4种方法都要优于常规梯形积分方法,第一类Neumann方法与常规梯形积分方法差距最大,差距最大可达-0.6 nm/s。由于GRACE距离变率的精度约为0.2~0.3 μm/s,该差距量级对于GRACE卫星重力反演起不到作用,但对于GRACE-FO和NGGM的nm级的星间距离和亚nm级的距离变率测量,势必存在影响。最小二乘方法和第二类Neumann方法在靠近北极处与常规梯形积分方法的差距为正值,最大可达0.4 nm/s,说明这两种方法在靠近北极处的精度要低于常规梯形积分方法。

|
图 3 4种方法与常规球谐分析方法的星间距离变率残差之差 Fig. 3 Range rate residual differences between traditional method and other four methods |
为进一步比较5种球谐分析方法的差别,基于2007-01的GRACE星间距离变率数据,对5种策略所反演的6组60阶次时变地球重力场模型进行分析。以最新的EIGEN-6C4[18]作为参考模型,比较这5组模型与参考模型之间的差距,计算60阶次的累计大地水准面误差(表 4)。可以看出,5组模型计算的累计大地水准面误差基本一致,差距在μm量级,其中第一类Neumann方法误差最小,精度最高,与上述第一类Neumann方法星间距离变率残差最小相一致,其累计误差与误差最大的最小二乘方法差距为1.4 μm,这种差距对于GRACE实际应用来说完全可以忽略不计。
|
|
表 4 60阶累计大地水准面误差 Tab. 4 Cumulated geoid height errors up to 60 degree |
值得说明的是,表 4与图 3对比4种方法的精度差异存在矛盾。原因在于不管是计算星间距离变率残差还是计算时变重力场模型,除了受大气去混频模型的影响外,还受其他很多因素的影响,如弧段边界轨道误差、加速度计偏差尺度误差、其他力模型误差、反演数学模型误差、参考模型误差等,所以计算星间距离变率和时变重力场模型只能在一定程度上反映大气去混频模型的精度,故表 4与图 3存在不一致性,但第一类Neumann分析方法精度最高的结论是一致的。
4 结语球谐分析作为计算大气与海洋去混频模型的重要过程,不同球谐分析方法必然会得到不同质量变化的去混频模型。本文从球谐分析的解析积分公式出发,导出了5种适用于大气去混频模型计算的球谐分析数值计算公式,并采用模拟数据及实测数据计算,来验证不同球谐分析方法所计算去混频模型的效果。从模拟数据比较来看,第一类Neumann方法和最小二乘方法所计算模型的谱域及空域均方根最小,最适合于球谐分析计算,第一类Neumann方法抵抗误差的能力最强。从实际数据来看,虽然第一类Neumann方法需要对等间隔格网数据进行内插,但其所计算的星间距离变率残差和累计大地水准面误差仍然最小,优于其他4种球谐分析方法。虽然不同球谐分析方法之间的差距要小于GRACE本身观测值的精度,不会对现有GRACE卫星重力恢复产生直接影响,但GRACE数据处理方法一直在不断改进更新,时变重力场模型产品已发布到RL05版本,球谐分析方法势必对大气与海洋去混频模型计算和未来GRACE重力场模型计算产生潜在影响。尤其对于未来GRACE-FO及NGGM的卫星重力任务,不同球谐分析方法的差距已达到激光测距观测值精度水平。本文只分析了大气去混频模型计算,对于海洋去混频模型计算,只需要将大气压力更换为海洋底部压力即可。因此,建议大气与海洋去混频模型的计算采用第一类Neumann方法。
| [1] |
Kusche J, Klemann V, Bosch W. Mass Distribution and Mass Transport in the Earth System[J]. Journal of Geodynamics, 2012, 59/60: 1-8 DOI:10.1016/j.jog.2012.03.003
(  0) 0) |
| [2] |
Tapley B D, Bettadpur S, Ries J C, et al. GRACE Measurements of Mass Variability in the Earth System[J]. Science, 2004, 305: 503-505 DOI:10.1126/science.1099192
(  0) 0) |
| [3] |
卢飞, 游为, 范东明, 等. 基于GRACE RL05数据分析近十年中国大陆水储量及海水质量变化[J]. 测绘学报, 2015, 44(2): 160-167 (Lu Fei, You Wei, Fan Dongming, et al. Chinese Continental Water Storage and Ocean Water Mass Variations and Analysis in Recent Ten Years Based on GRACE RL05 Data[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(2): 160-167)
(  0) 0) |
| [4] |
Forootan E, Didova O, Kusche J, et al. Comparisons of Atmospheric Data and Reduction Methods for the Analysis of Satellite Gravimetry Observations[J]. Journal of Geophysical Research: Solid Earth, 2013, 118: 1-15
(  0) 0) |
| [5] |
Ditmar P, Encarnacao J, Farahani H. Understanding Data Noise in Gravity Field Recovery on Basis of Inter-Satellite Ranging Measurements Acquired by the Satellite Gravimetry Mission GRACE[J]. J Geod, 2012, 86: 441-465 DOI:10.1007/s00190-011-0531-6
(  0) 0) |
| [6] |
Wiese D N. Optimizing Two Pairs of GRACE-Like Satellites for Recovering Temporal Gravity Variations[D]. Boulder: University of Colorado, 2011
(  0) 0) |
| [7] |
Hwang C, Kao Y. Spherical Harmonic Analysis and Synthesis Using FFT: Application to Temporal Gravity Variation[J]. Computers & Geosciences, 2006, 32: 442-451
(  0) 0) |
| [8] |
Sneeuw N. Global Spherical Harmonic Analysis by Least-Squares and Numerical Quadrature Methods in Historical Perspective[J]. Geophys J Int, 1994, 118: 707-716 DOI:10.1111/gji.1994.118.issue-3
(  0) 0) |
| [9] |
Colombo O L. Numerical Methods for Harmonic Analysis on the Sphere[R]. Ohio: The Ohio State University, 1981
(  0) 0) |
| [10] |
Flechtner F, Dobslaw H, Fagiolini E. AOD1B Product Description Document for Product Release 05[R]. Potsdam: GFZ German Research Centre for Geosciences, 2014
(  0) 0) |
| [11] |
Zenner L. Atmospheric and Oceanic Mass Variations and Their Role for Gravity Field Determination[D]. München: Technischen Universität München, 2013
(  0) 0) |
| [12] |
Driscoll J R, Healy D M. Computing Fourier Transforms and Convolutions on the 2-Sphere[J]. Advances in Applied Mathematics, 1994, 15: 202-250 DOI:10.1006/aama.1994.1008
(  0) 0) |
| [13] |
Dee D P, Uppala S M, Simmons A J, et al. The ERA-Interim Reanalysis: Configuration and Performance of the Data Assimilation System[J]. QJR Meteorol Soc, 2011, 137: 553-597 DOI:10.1002/qj.v137.656
(  0) 0) |
| [14] |
Mayer-Gürr T. Gravitations Feld Bestimmung aus der Analyse Kurzer Bahnboegen am Beispiel der Satellitenmissionen CHAMP und GRACE[D]. Bonn: Institute fuer Theoretische Geodaesi der Universitaet Bonn, 2006
(  0) 0) |
| [15] |
游为, 范东明, 黄强. 卫星重力反演的短弧长积分法研究[J]. 地球物理学报, 2011, 54(11): 2745-2752 (You Wei, Fan Dongming, Huang Qiang. Analysis of Short-Arc Integral Approach to Recover the Earth's Gravitational Field[J]. Chinese J Geophys, 2011, 54(11): 2745-2752 DOI:10.3969/j.issn.0001-5733.2011.11.004)
(  0) 0) |
| [16] |
Rieser D, Mayer-Gürr T. The Ocean Tide Model EOT11a in Spherical Harmonics Representation[R]. Graz: Institute of Theoretical Geodesy and Satellite Geodesy(ITSG), 2012
(  0) 0) |
| [17] |
Biancale R, Bode A. Mean Annual and Seasonal Atmospheric Tide Models Based on 3-Hourly and 6-Hourly ECMWF Surface Pressure Data[R]. Potsdam: GFZ German Research Centre for Geosciences, 2006
(  0) 0) |
| [18] |
Förste C, Bruinsma S L, Abrikosov O, et al.EIGEN-6C4 The Latest Combined Global Gravity Field Model Including GOCE Data up to Degree and Order 2190 of GFZ Potsdam and GRGS Toulouse[EB/OL].http://dx.doi.org/10.5880/icgem, 2015
(  0) 0) |
 2017, Vol. 37
2017, Vol. 37





