2. 内蒙古科技大学矿业与煤炭学院,包头市阿尔丁大街7号,014010;
3. 江门市勘测院有限公司,江门市农林西路25号,529000
总体最小二乘(TLS)方法能够同时考虑观测向量和系数矩阵的误差,相比最小二乘方法可以得到更加可靠的解算结果。当系数矩阵的列向量间呈近似线性相关时,观测量的微小变化会引起解的巨大波动,截断奇异值法[1]和Tikhonov正则化[2]是解决此类问题的有效方法。根据文献[3],TLS的求解过程为一个降正则化过程,因此在TLS解算中,系数矩阵的病态不仅导致求解参数的不稳定,并且随着病态性的加强,其求解的不稳定性也逐步增大[4]。文献[2]提出TLS的正则化解,给出取不同约束参数时正则化总体最小二乘解(RTLS)与TLS解的关系。文献[5]将RTLS的求解转换为求矩阵的特征向量问题,并给出RTLS的迭代解法。文献[6]将RTLS问题转换成一个闭区间内的单变量函数的最小化问题。文献[7]采用岭估计方法解决加权总体最小二乘平差的病态性问题。文献[8]根据广义最小二乘原理,得到病态总体最小二乘平差的虚拟观测法。文献[9]基于Tikhonov正则化原理,推导了等权条件下病态总体最小二乘的迭代解法。文献[10]基于L曲线法提出解病态总体最小二乘的广义正则化方法。文献[4]推导了基于误差限的TLS正则化算法。文献[7-8]对病态总体最小二乘的处理均是基于经典测量平差理论,与文献[11]提出的最小二乘正则化L曲线法相比,其解算精度并无明显提高。文献[4, 9-10]均是基于Tikhonov正则化原理得到RTLS解,然而,利用单一的Tikhonov正则化算法会造成求解过度平滑,以致得不到稳定、精确的解。
总变差(TV)正则化可以更有效地抵抗噪声。文献[12-13]利用Tikhonov正则化和TV正则化分别反演电离层电子密度。文献[14]给出了病态最小二乘的TV正则化迭代算法。
本文基于文献[15]提出的最小-最大残差法,并结合文献[12-14]提出的TV正则化算法,推导了一种基于Tikhonov正则化和总变差正则化组合的混合正则化算法。最后通过算例说明本文所提方法的可行性和有效性。
1 混合正则化方法 1.1 总体最小二乘的正则化设线性平差模型为:

|
(1) |
式中, b为观测向量;eb为观测向量对应的随机误差向量;A为系数矩阵;EA为系数矩阵A的随机误差矩阵,且eA=vec(EA),vec(·)为拉直运算;x为未知参数向量。当系数矩阵的列向量间存在复共线性时,观测量出现的轻微扰动会造成总体最小二乘解的极大变化,使得解不稳定,因此有必要研究病态TLS的数据处理问题。
文献[4]利用最小-最大残差法推导了总体最小二乘的正则化算法。当设计矩阵和观测向量的误差上限已知时,RTLS的平差准则可表示为:

|
(2) |
式中,ΔA、Δ b分别为系数矩阵和观测向量的随机误差;L为正则化约束条件的系数矩阵,通常是一阶或二阶差分算子;δ为正常数;η、ηb分别为系数矩阵和观测向量的误差上限值。
针对有界不确定性观测数据进行平差,文献[15]建立了min-max平差准则:

|
(3) |
根据范数的性质,有:
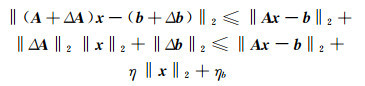
|
(4) |
由式(3)和式(4)可知:

|
(5) |
根据式(3)和式(5),不确定性min-max平差准则可以转换成另一形式的平差准则:
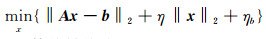
|
(6) |
则式(2)可等价转换为:
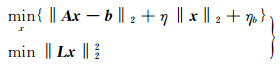
|
(7) |
目标函数式为:
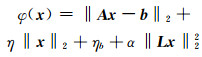
|
(8) |
将式(8)对x求导并令其等于0,可得:

|
(9) |
式中,

|
(10) |
本文将Tikhonov正则化和TV正则化两种方法有效结合,推导出一种新的混合正则化算法。其约束条件式表示为:
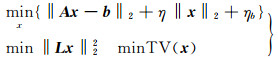
|
(11) |
目标函数式为:

|
(12) |
式中,α、β为正则化参数。由于TV(x)不可微,因此对于二维连续总变差泛函,TV(x)近似表示为:
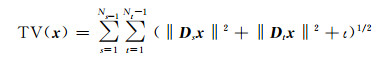
|
(13) |
对于三维情形,TV(x)表示为:
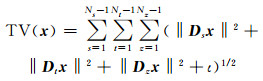
|
(14) |
式中,Ns、Nt和Nz分别为沿x、y和z方向的网格数;Ds、Dt和Dz分别为x、y和z方向的一阶或二阶差分算子:水平方向上Dsx= xs+1, t, z-xs, t, z,Dtx=xs, t+1, z-xs, t, z,垂直方向上Dzx=xs, t, z+1-xs, t, z;ι为一小的正数。
根据文献[16],将式(13)、式(14)转化为l2范数正则化项,可记为:
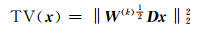
|
(15) |
对于二维情形,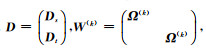

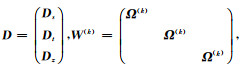
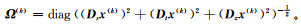
将式(12)对x求导并令其等于0,可得:

|
(16) |
整理得:
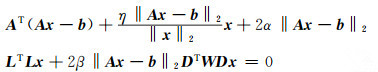
|
(17) |

|
(18) |
式中,
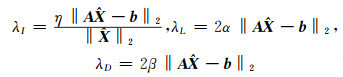
|
(19) |
正则化参数α、β可由最大验后估计法确定:
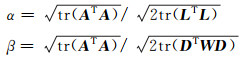
|
(20) |
本文所提方法的迭代步骤如下:
1) 利用最小二乘法求得参数xLS作为迭代的初值。
2) 确定系数矩阵误差上限值η。当系数矩阵和观测向量的真值已知时,经计算可以获得相应的误差上限值;当系数矩阵和观测向量的真值未知时,可根据仪器标称精度确定误差上限。
3) 根据式(20)计算正则化参数α、β。
4) 利用初始值、误差上限值及正则化参数α、β,根据式(19)分别求解λI、λL和λD的初值。
5) 利用式(18)计算正则化总体最小二乘解xRTLS。
6) 重复步骤4)、5),直至‖ x (k+1)-x(k)‖<ε, 迭代终止。
2 算例分析模型的系数矩阵和观测向量数据见文献[17],待求参数5个,真值均为1。用Matlab分别对观测向量b和设计矩阵A的每个元素添加均值为0、方差为σ2的随机误差,即eb~N(0, σ2I),eA=vec(EA)~N(0, σ2In⊗Im),其中σ=0.1。加入随机误差的系数矩阵和观测向量为:

|
法方程条件数cond(ATA)=2.083 7×104,系数矩阵严重病态。经计算,‖δA ‖2=0.427 5<0.5,‖δb ‖2=0.231 9<0.25,因此设η=0.5,ηb=0.25。为了比较不同情况下解的差异,分别采用最小二乘法(LS)、正则化最小二乘法(RLS)、总体最小二乘法(TLS)、正则化总体最小二乘法[18](RTLS)、文献[4]提出的误差限病态总体最小二乘法(简称葛旭明法)和本文方法进行参数解算,并计算不同方法所得结果
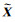
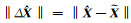

|
|
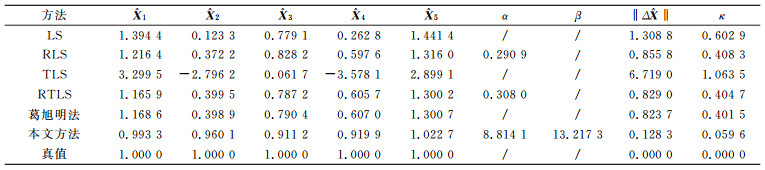
表 1 模型参数X的计算结果 Tab. 1 Results of model parameter X |
1) 当系数矩阵A病态时,总体最小二乘解与真值的差值范数为6.719 0,较最小二乘解与真值的差值范数1.308 8要大,说明总体最小二乘解受病态影响更为严重。
2) RTLS解与真值的差值范数为0.829 0,较RLS解与真值的差值范数0.855 8无明显提高,这主要是因为在计算过程中,正则化约束系数矩阵L为单位阵,当δ足够小时,病态TLS的约束条件退化为LS的约束条件。说明在处理病态总体最小二乘问题时,标准正则化方法相对最小二乘正则化方法并无明显优势。
3) 混合正则化算法在约束条件中加入TV正则化约束,相对于葛旭明算法其精度提高了84.4%。说明本文方法在处理病态总体最小二乘问题上是可行的,并且具有较高的稳定性。
4) 在计算过程中,混合正则化算法避免了正常数δ的引入,因而解算结果更加可靠。
3 结语本文将Tikhonov正则化和TV正则化两种方法有效结合,提出一种混合正则化算法,并推导了求解的具体公式和迭代算法。该方法利用范数的性质,将病态总体最小二乘的约束条件进行转换,从而建立目标函数,通过求导的方法得到参数的解。由算例可以看出,本文提出的方法可以有效地处理总体最小二乘的病态问题。关于不等精度观测、系数矩阵仅部分元素含随机误差的情形,其解算公式的推导将是下一步研究的工作。
| [1] |
Fierro R D, Golub G H, Hansen P C, et al. Regularization by Truncated Total Least Squares[J]. SIAM Journal on Scientific Computing, 1997, 18(1): 1223-1241
(  0) 0) |
| [2] |
Golub G H, Hansen P C, O'Leary D P. Tikhonov Regularization and Total Least Squares[J]. SIAM Journal on Matrix Analysis and Applications, 1999, 21(1): 185-194 DOI:10.1137/S0895479897326432
(  0) 0) |
| [3] |
Golub G H, Loan C F. An Analysis of the Total Least Squares Problem[J]. SIAM Journal on Numerical Analysis, 1980, 17(6): 883-893 DOI:10.1137/0717073
(  0) 0) |
| [4] |
葛旭明, 伍吉仓. 误差限的病态总体最小二乘解算[J]. 测绘学报, 2013, 42(2): 192-202 (Ge Xuming, Wu Jicang. A Regularization Method to Ill-Posed Total Least Squares with Error Limits[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(2): 192-202)
(  0) 0) |
| [5] |
Guo H B, Renaut R A. A Regularized Total Least Squares Algorithm[A]//Total Least Squares and Errors-in-Variables Modeling[M]. Copenhagen: Kluwer Academic Publishers, 2002
(  0) 0) |
| [6] |
Beck A, Bental A. On the Solution of the Tikhonov Regularization of the Total Least Squares Problem[J]. SIAM Journal on Optimization, 2006, 17(1): 98-118 DOI:10.1137/050624418
(  0) 0) |
| [7] |
王乐洋, 许才军, 鲁铁定. 病态加权总体最小二乘平差的岭估计方法[J]. 武汉大学学报:信息科学版, 2010, 35(11): 1346-1350 (Wang Leyang, Xu Caijun, Lu Tieding. Ridge Estimation Method in Ill-Posed Weighted Total Least Squares Adjustment[J]. Geomatics and Information Science of Wuhan University, 2010, 35(11): 1346-1350)
(  0) 0) |
| [8] |
王乐洋, 于冬冬. 病态总体最小二乘问题的虚拟观测解法[J]. 测绘学报, 2014, 43(6): 575-581 (Wang Leyang, Yu Dongdong. Virtual Observation Method to Ill-Posed Total Least Squares Problem[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(6): 575-581)
(  0) 0) |
| [9] |
袁振超, 沈云中, 周泽波. 病态总体最小二乘模型的正则化算法[J]. 大地测量与地球动力学, 2009, 29(2): 131-134 (Yuan Zhenchao, Shen Yunzhong, Zhou Zebo. Regularized Total Least Squares Solution to Ill-Posed Error-In-Variable Model[J]. Journal of Geodesy and Geodynamics, 2009, 29(2): 131-134)
(  0) 0) |
| [10] |
葛旭明, 伍吉仓. 病态总体最小二乘问题的广义正则化[J]. 测绘学报, 2012, 41(3): 372-377 (Ge Xuming, Wu Jicang. Generalized Regularization to Ill-Posed Total Least Squares Problem[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 372-377)
(  0) 0) |
| [11] |
Hansen P C. Analysis of Discrete Ill-Posed Problems by Means of the L-Curve[J]. SIAM Review, 1992, 34(4): 561-580 DOI:10.1137/1034115
(  0) 0) |
| [12] |
Lee J K, Kamalabadi F, Makela J J. Localized Three-Dimensional Ionospheric Tomography with GPS Ground Receiver Measurements[J]. Radio Science, 2007, 42(4): 229-238
(  0) 0) |
| [13] |
Lee J K, Kamalabadi F, Makela J J. Three-Dimensional to Tomography of Ionospheric Variability Using a Dense GPS Receiver Array[J]. Radio Science, 2008, 43(3): 2711-2726
(  0) 0) |
| [14] |
Yao Y B, Tang J, Kong J, et al. Application of Hybrid Regularization Method for Tomographic Reconstruction of Midlatitude Ionospheric Electron Density[J]. Advanced in Space Research, 2013, 52(12): 2215-2225 DOI:10.1016/j.asr.2013.09.030
(  0) 0) |
| [15] |
宋迎春, 谢雪梅, 陈晓林. 不确定性平差模型的平差准则与解算方法[J]. 测绘学报, 2015, 44(2): 135-141 (Song Yingchun, Xie Xuemei, Chen Xiaolin. Adjustment Criterion and Algorithm in Adjustment Model with Uncertainty[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(2): 135-141)
(  0) 0) |
| [16] |
何进荣.基于加权范数迭代算法的总变差正则化图像复原方法[D].武汉: 武汉理工大学, 2011 (He Jinrong. Total Variation Regularization of Image Restoration Based on Iteratively Reweighted Norm Algorithm[D]. Wuhan: Wuhan University of Technology, 2011)
(  0) 0) |
| [17] |
鲁铁定, 宁津生. 总体最小二乘平差理论及其应用[M]. 北京: 中国科学技术出版社, 2011 (Lu Tieding, Ning Jinsheng. Total Least Squares Adjustment Theory and Its Applications[M]. Beijing: China Science and Technology Press, 2011)
(  0) 0) |
2. Mining and Coal Institute, Inner Mongolia University of Science and Technology, 7 Arding Street, Baotou 014010, China;
3. Jiangmen Investigation and Surveying Institute Co Ltd, 25 West-Nonglin Road, Jiangmen 529000, China
 2017, Vol. 37
2017, Vol. 37