2. 中国科学院大学,北京市玉泉路甲19号, 100049;
3. 地壳运动监测工程研究中心,北京市三里河路56号,100036
青藏高原是全球中低纬度地区最大的现代冰川区,对气候变化非常敏感。利用GRACE卫星重力反演青藏高原及其邻区陆地水储量变化(terrestrial water storage change, TWSC),分离水文循环要素,对水资源管理、全球变化研究具有重要意义[1]。
反演TWSC一般利用发布的二级数据,即重力场球谐模型进行。受卫星轨道误差和测量误差影响,GRACE重力场模型存在条带误差和高阶误差。对条带误差一般采用去相关滤波[2-4]。对高阶误差则是进行高斯滤波[5]或扇形滤波[6]。不同研究者反演的青藏高原TWSC差异较大。Zhong等[7]利用2002~2007数据,结合高斯滤波得到青海-四川-甘肃交界处和阿尔金山区的两个正趋势信号;Matsuo[8]采用5次多项式拟合去相关滤波及400 km半径高斯滤波,用2002-08~2009-04重力数据反演,发现横贯高原的一个大的正信号;朱传东等[9]采用固定宽度为7的滑动窗口、3次多项式拟合去相关滤波及350 km半径高斯滤波,用2002~2013年重力数据反演,发现高原中心存在较大范围的TWSC正趋势信号;刘杰等[10]采用5次多项式拟合处理15次以上重力场系数,结合200 km扇形滤波,用2003~2013年重力数据发现高原中部及柴达木盆地位置的两个正的重力趋势信号。反演TWSC的较新途径是利用星间距测速结果进行质量(Mascon)反演[11],由于反演过程需要水文学模型和冰川测量等先验约束,而恰恰在青藏高原水文学模型非常不确定[12],冰川测量结果也具有较大的不确定性。因此,Mascon结果能否很好地反映高原TWSC,值得怀疑。
本文利用不同类型的GRACE数据,结合不同的后处理方法反演TWSC,并将反演结果彼此之间、与卫星测高观测结果及降水模型结果进行对比,讨论各种滤波方法的优劣、GRACE数据选择的影响,推荐适合本区反演的后处理方法与GRACE数据。
1 数据和处理方法 1.1 GRACE数据 1.1.1 重力场球谐模型本文采用德克萨斯大学空间研究中心(CSR)、波茨坦地学中心(GFZ)和NASA喷气动力实验室(JPL)发布的RL05 GRACE球谐重力模型,研究时段为2003-01~2009-12,与ICESat_1卫星测高观测时段一致。重力场数据已扣除非潮汐大气、高频海洋信号、海洋大气潮汐、海潮、固体潮、固体极潮等的影响,主要反映陆地水随时间的变化。针对3组GRACE重力场数据,使用前60阶Stokes系数,C20用SLR观测值代替[13],一阶项采用Swenson等[14]的结果。
选用CSR重力场数据,将Stokes系数分为奇偶两部分,以阶数l为自变量分别对固定次数m进行多项式拟合,把拟合值作为条带误差改正项从Stokes系数中扣除[15],选择不同的去相关起始次数、拟合多项式次数p和滤波窗口宽度w,研究TWSC反演结果的可变性。去相关滤波前,需先将Stokes系数时间序列扣除2003~2009年的平均值。
去相关起始次数取m=6、8、10次,多项式次数取p=2、3、4次, 窗口宽度w按不采用滑动窗口、固定宽度滑动窗口和变宽度滑动窗口3种类型赋值。以起始次数为8、二次多项式拟合(即P2M8)为例:①不采用滑动窗口[2],次数m<8的Stokes系数保持不变,即m≥8的Stokes系数同一次的所有偶(奇)数阶进行二次多项式拟合;②采用固定宽度滑动窗口,取宽度w=7;③采用变宽度滑动窗口,窗口宽度w分别根据式(1)、式(2)计算[3-4]:
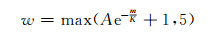
|
(1) |
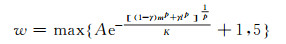
|
(2) |
式(1)中,经验参数A=30,K=10;式(2)中A=30,p=3,γ=0.1,K=15。
根据Geruo等[16]的冰川均衡调整(GIA)模型,在去相关处理的Stokes系数中扣除GIA的影响,可用于反演TWSC[17]:
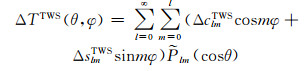
|
(3) |
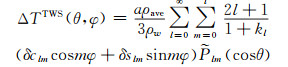
|
(4) |
式中,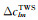
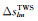
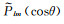
分别使用高斯滤波[5]和扇形滤波[6]压制高阶误差。高斯滤波需在式(3)或(4)中加入随阶数l变化的高斯滤波权重因子wl;扇形滤波加入随阶数l和次数m变化的高斯滤波权重因子wl和wm,滤波半径均采用340 km。
应该指出,式(3)、(4)的有限截断和滤波器的引入都造成信号泄漏,一般需要进行信号恢复处理[18], 而本文不进行该处理,因为我们对GRACE监测的TWSC和卫星测高结果均用式(3)同样的球谐表达,通过比较可以显示结果的可变性以及滤波器和数据的合理性。
1.1.2 质量(Mascon)模型Mascon模型采用2015年JPL发布的GRACE Mascon解RL05M[11],数据时段为2003~2009。根据Watkins等[11]在全球划定的4 551个质量均匀分布的3°等面积球帽(Mascon),利用JPL重力场Level-1数据,通过加权最小二乘方法得到每个球帽的等效水柱高值,确定权矩阵用到了GIA模型[16]、GLDAS水文模型[19]等约束;用CLM 4.0[20]水文模型获取一组0.5°×0.5°尺度因子,作用于Mascon的结果,以提高空间分辨率(图 1)。Mascon解算过程中因为用地球物理约束来抑制条带误差,所以不需要去相关滤波处理[11]。

|
图 1 根据MAS和MAS_S数据计算的TWSC趋势((a)、(b), 单位mm/a)和周年振幅((c)、(d),单位mm) Fig. 1 Trend rates and the annual amplitudes using MAS and MAS_S Mascon data |
为了方便与前述基于GRACE球谐模型的反演结果对比,需要对MAS和MAS_S给出的EWT时间序列结果作处理。先对其进行球谐分析[21],球谐展开截断至60阶,然后用式(3)计算空间域1°×1°网格中心的结果,进一步对空间域时间序列用常数项、线性项、季节项进行最小二乘回归分析,得到趋势速率和周年振幅。
1.2 降水数据全球降水气候学计划(GPCP)能提供全球2.5°×2.5°网格的降水模型数据[22]。本文利用2003~2009年的月降水资料球谐分析和求和计算[21],球谐截断至60阶,得到空间域1°×1°网格结果。进一步作累积距平处理,并作最小二乘回归分析。
1.3 卫星测高结果 1.3.1 冰质量变化根据Gardner等[23]的卫星测高结果,对除喀喇昆仑外的所有子区域的冰川,合理地布置957个等效点质量,在同一子区域内的各点质量具有相同的质量变化速率(图 2(o))。进一步根据点质量及其位置(经纬度)通过式(5)得到球谐展开系数,并利用式(3)得到空间域1°×1°网格的冰质量变化趋势速率:
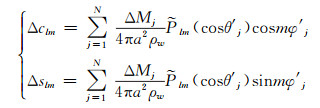
|
(5) |

|
图 2 不同去相关滤波方法对TWSC趋势反演的影响 Fig. 2 Effects of destriping method selections on the inverted trend rates of TWSC (a)~(l)不同去相关滤波处理的Stokes系数反演的TWSC趋势, (m)没有去相关滤波的结果, (n)和(o)湖水和冰川质量变化趋势(截断至60阶), 单位mm/a. (a)~(c)利用Chamber方法不同多项式次的结果(起始次为8);(d)~(f)利用固定宽度滑动窗口不同多项式次的结果; (g)~(i)是利用S & W变宽度滑动窗口不同多项式次的结果; (j)-(l)利用Duan变宽度滑动窗口不同多项式次的结果. (n)(o)观测的异常信号分别用A~F编号的封闭图形标出, 红色、白色代表湖、冰 |
式中,N为点质量总数, N=957;ΔMj为第j个点质量(即质量变化速率);θ′j、φ′j分别为第j个点质量的余纬和经度。
1.3.2 湖水质量变化Zhang等[24]利用2003~2009年的ICESat-1测高数据及SRTM高程数据,得到青藏高原内部200个湖的地理位置、湖面面积及湖水高程变化趋势。利用湖面面积和水面高程变化趋势计算每个湖的质量变化趋势速率。由于GRACE卫星数据难以分辨小于100 000 km2的目标,所以可把每个湖看作离散的点质量。在同一时段,收集到天山周围19个湖(包含7个水库)的经纬度位置和湖水质量变化数据[1],除Balkhash湖和Issyk Kul湖分割成若干离散点质量外,每个湖作为一个点质量。依此,得到青藏高原及天山周围共257个等效点质量及其位置,根据式(3)、(5)可以得到空间域1°×1°网格的湖水质量变化趋势速率(图 2(n))。
2 结果与分析 2.1 滤波方法选择对TWSC趋势反演的影响 2.1.1 去相关滤波采用CSR重力场数据,去相关滤波分别用不采用滑动窗口(Chamber)、固定宽度滑动窗口(Fixed W7,宽度w=7)、S & W变宽度滑动窗口(宽度只与次数有关)、Duan变宽度滑动窗口(宽度与阶数和次数有关),每个去相关滤波起始次数均为m=8,拟合多项式次数分别取p=2、3、4次。将利用经去相关处理后的Stokes系数的TWSC反演结果(图 2(a)~(l)),与不作去相关滤波处理的反演结果(图 2(m))以及卫星测高观测结果进行对比(图 2(n)、(o))。
可以看出,任何一种去相关滤波方法都对条带误差有不同程度的压制作用,不采用滑动窗口(图 2(a)~(c))去条带效果不理想,固定宽度滑动窗口(图 2(d)~(f))效果最差,变宽度滑动窗口(图 2(g)~(l))效果相对较好。随着拟合多项式次数的增加,固定宽度滑动窗口(图 2(d)~(f))的条带明显增加,而Chamber窗口和S & W及Duan窗口的结果变化不大。以湖水和冰质量变化趋势(图 2(n)、(o))为基准,检验图(a)~(l)不同滤波和拟合多项式次数组合的结果,发现变宽度滑动窗口去相关滤波方法(图 2(g)~(l))较适合该区域,图 2(n)中湖水变化区域A、C、F,图 2(o)中冰的质量变化区域B、C、D、E,均可以找到相应信号,但S & W P2M8(图 2(g))去相关滤波无论异常信号位置、形态还是幅值符合最好,所以这种去相关滤波最优。
此外,本文采用S & W变宽度滑动窗口去相关滤波和二次多项式拟合,选取不同的去相关起始次数(6、8、10次)研究其影响。起始次数取6次(图 3(a))和10次(图 3(b))相对8次(图 2(g))的差值较小(图 3(c)、(d)),统计较强的信号差异不超过7%,起始次数的选择对反演趋势结果影响较小。

|
图 3 去相关起始次数对TWSC趋势反演结果的影响 Fig. 3 Effects of the start order selections for destriping on the inverted TWSC trend rates (a)、(b)表示用S & W法分别对6次和10次起Stokes系数去相关滤波后TWSC趋势反演结果, 去相关回归均用二次多项式; (c)、(d)分别为其结果与起始次数为8时(Fig.2g)的差异, 单位mm/a |
高斯滤波(图 4)和扇形滤波(图 5)都可以有效压制高阶误差,起到平滑信号的作用。统计几个主要异常,高斯滤波的结果幅值与扇形滤波相差10%~30%。

|
图 4 图 2(a)、(g)、(j)、(m)、(n)、(o)高斯滤波后的结果(mm/a) Fig. 4 Results of Fig. 2(a)、(g)、(j)、(m)、(n)、(o)after Gaussian filter is used |
|
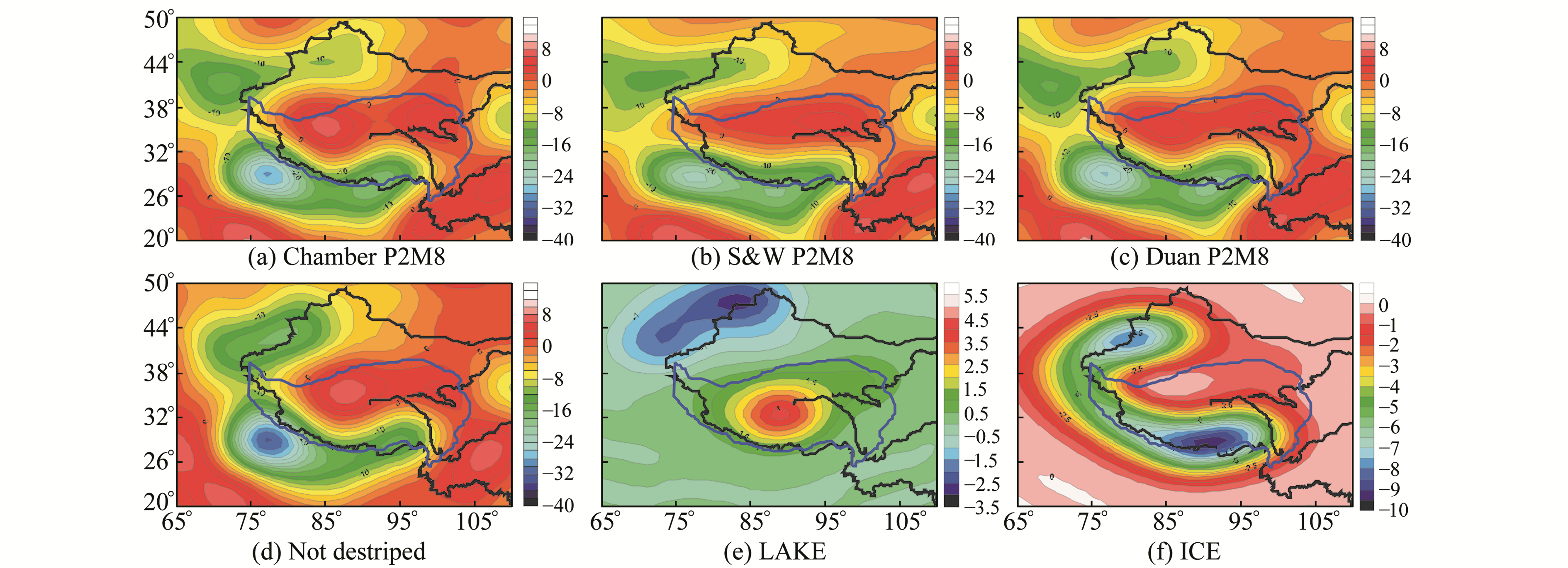
图 5 图 2(a)、(g)、(j)、(m)、(n)(o)扇形滤波后的结果(单位mm/a) Fig. 5 Results of Fig. 2(a)、(g)、(j)、(m)、(n)(o) after Fan filter is used |
对于青藏高原地区,不进行平滑滤波,可以较好地反映卫星测高观测的湖水与冰川信号(图 2(n)、(o))。高斯平滑滤波后,湖水和冰信号变得模糊甚至消失(图 4(b))。将图 4(e)、(f)与图 2(n)、(o)比较,也可看出平滑滤波对湖水和冰川信号有削弱作用。
图 4(a)、(b)、(c)分别对应Chamber、S & W和Duan与高斯滤波进行的组合滤波。其相互差异是,Chamber在青藏高原西北部有一个较大幅值的正信号,而S & W没有此独立分布的信号,Duan结果介于两者之间;相同之处是,在长江与黄河源头有一个正信号、在印度西北部平原和孟加拉盆地均各有一个负值信号。比较图 2(a)与图 2(m),平滑滤波前,Chamber去条带效果较差。另外,比较图 4(d)与图 2(m),完全不去条带但平滑滤波后在高原西北部也出现一个较大的正异常,一定程度上说明图 4(a)Chamber滤波得到的该正信号可能受条带误差影响。鉴于平滑滤波之前S & W去相关滤波结果(图 2(g))较好地反映了湖水和冰川信号,所以我们认为S & W+平滑滤波器的组合滤波结果较好(图 4(b))。
2.2 数据选择对TWSC趋势反演的影响Stokes数据,结果见图 2(g)与图 6(a)、(b),另选用JPL两个版本的质量模型MAS/MAS_S,结果见图 6(c)、(d)。此外,还给出了它们经高斯滤波后的结果,见图 4(b)和图 6(e)~(h)。

|
图 6 不同数据源对TWSC趋势反演的影响 Fig. 6 Effects of data source selections on the TWSC trend rates (a)~(d)为分别利用GFZ、JPL、MAS(截断到60阶Stokes系数)和MAS_S数据(同上)反演TWSC趋势(e)~(h)为(a)~(d)对应高斯滤波后的结果, 单位mm/a |
对CSR/GFZ/JPL重力场数据只作去相关滤波处理时,其反演结果总体相近(图 2(g), 图 6(a)、(b)),仅在部分区域存在差异,如西昆仑地区(黑色矩形框),JPL数据的反演结果没有形成独立的信号;念青唐古拉山东部地区(品红色矩形框)负信号分布不同,GFZ数据反演结果是相对独立的信号,而CSR和JPL数据反演结果跟东喜马拉雅负信号连接在一起;喜马拉雅山脉南部(黄色矩形框),GFZ和JPL数据反演结果相近,呈现两个相对独立的负信号,但CSR数据则没有。另外,GFZ数据反演结果(图 6(a))南北向条带相对明显些,且CSR数据反演结果(图 2(g))相比GFZ和JPL数据(图 6(a)、(b))更能反映卫星测高观测高原湖水和冰质量变化趋势结果(图 2(n)、(o))。因此在青藏高原地区,CSR数据较好。
两个质量模型MAS/MAS_S的信号分布较一致(图 6(c)、(d)),但幅值有差异:最大差异在高原西部,MAS信号中心幅值比MAS_S小35%(滤波后小15%),正是所谓水文尺度因子改善了模型分辨率的结果。3种RL05重力数据反演的结果与Mascon的结果差异很明显:前者基本上是在青藏高原内部有比较明显的3个正信号(图 2(g),图 6(a)、(b)),分别在高原东部、中南部和西北部(西昆仑地区),而后者在高原西部均有一个较大范围的正信号(图 6(c)、(d));在喜马拉雅山脉南部的负信号形态及位置有差异;在天山及帕米尔高原地区,RL05重力数据的反演结果为1个独立的负信号,而Mascon结果为2个独立的负信号。
进一步使用高斯滤波,CSR/GFZ/JPL 3种数据的反演结果基本一致(图 4(b)与图 6(e)、(f)),但与MAS/MAS_S的结果(图 6(g)、(h))差异较大,其原因可能是Mascon解算时先验水文约束条件在青藏高原的不确定性造成的,MAS_S需要的尺度因子也受该地区水文模型精度的限制。3种GRACE重力场数据反演结果在高原内基本上是横贯整个高原的正信号,信号的重心在黄河、长江源地区,在印度西北平原和孟加拉国地区有2个相对独立的负信号(图 4(g)和图 6(e)、(f)),Mascon结果在青藏高原西部存在1个大范围正信号,在印度西北平原有1个强负信号,沿喜马拉雅山脉走向有1个相对较弱的负信号(图 6(g)、(h))。
此外,MAS/MAS_S结果(图 6(g)、(h))与CSR不去条带结果(图 4(d))非常一致,这在很大程度说明原始的Mascon结果(图 1(a)、(b))已经包含条带的较大影响,其原因是受水文约束条件不确定性影响较大。因此,JPL的Mascon质量模型[11]不适合青藏高原及其邻近地区。
2.2.2 对TWSC振幅反演的影响CSR/GFZ/JPL RL05数据反演的时间序列周年振幅之间(图 7(a)、(c)、(e))及其高斯滤波后结果(图 7(b)、(d)、(f))基本一致,MAS/MAS_S数据高斯滤波前后(图 7(g)、(i)与图 7(h)、(j))也基本一致。RL05重力场数据反演的时间序列周年振幅(图 7(a)、(c)、(e))与Mascon的结果(图 7(g)、(i))存在差异:在MAS/MAS_S周年振幅结果中,青藏高原以南粉红色区域信号幅度比RL05重力数据的反演结果小约15%;黑色区域信号较RL05重力数据结果大得多;青藏高原以西黄色区域信号比RL05结果大约30%,信号形态也有不同。青藏高原以南的周年振幅信号可能与降水有关[25]。对比GPCP降水累积距平时间序列的周年振幅信号(图 8a)发现,该降水模型就异常位置分布支持RL05重力场数据的反演结果。对上述5个GRACE模型的反演结果和降水模型结果,分别进行高斯滤波,结果见图 7(b)、(d)、(f)、(h)、j和图 8(b)。可以看出同类模型的相似性和不同类模型之间的差异性,以及降水模型支持RL05模型的结论。
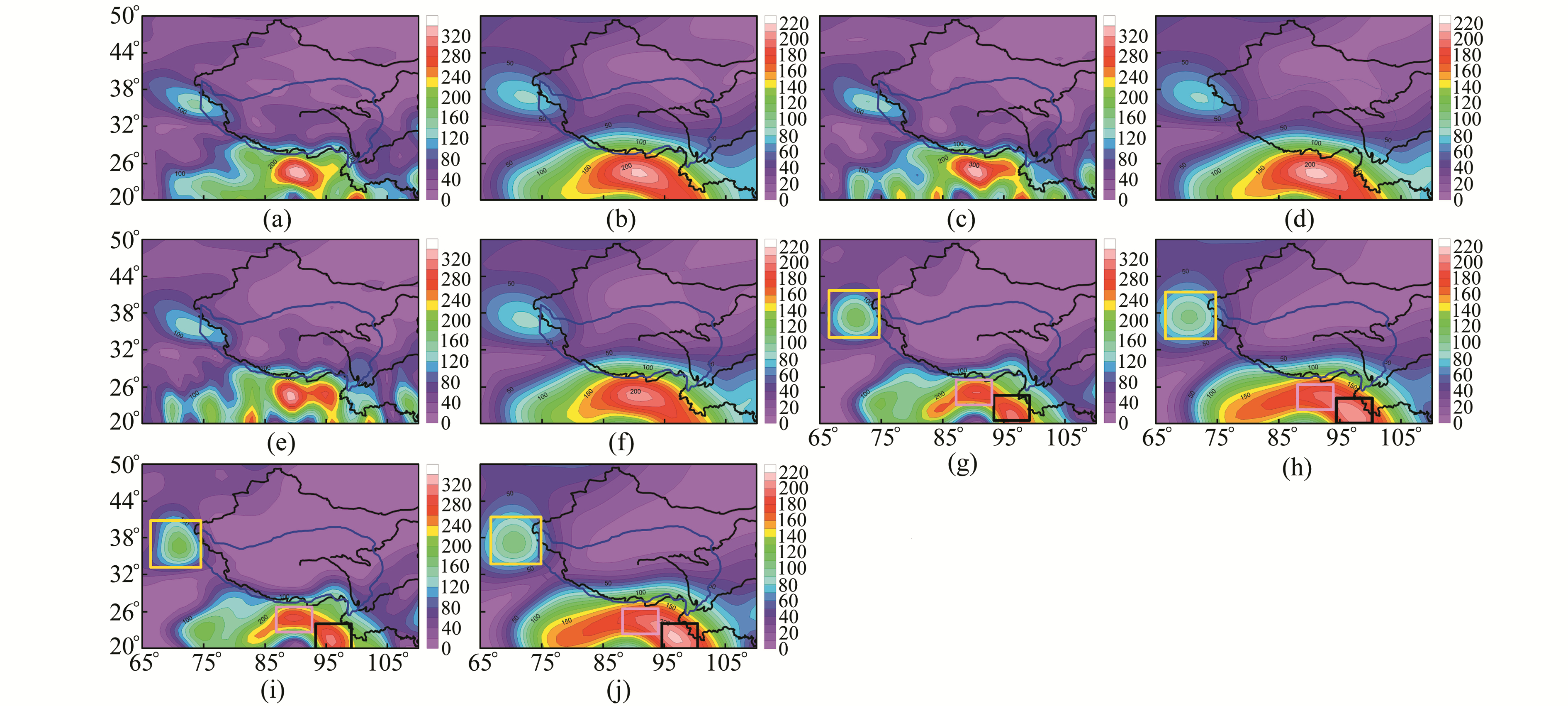
|
图 7 5种数据时间序列的周年振幅 Fig. 7 Annual amplitudes inverted from five different GRACE data (a)、(c)、(e)、(g)、(i)分别为CSR/GFZ/JPL/MAS/MAS_S时间序列的周年振幅; (b)、(d)、(f)、(h)、(j)分别为相应高斯滤波的结果, 单位mm (注:研究区域内海洋中的信号已做扣除处理) |

|
图 8 GPCP降水累积距平时间序列的周年振幅 Fig. 8 Amplitudes of accumulated precipitation anomalies derived from GPCP |
1) 在去相关滤波器中,不采用滑动窗口去条带效果不理想,采用固定宽度滑动窗口效果最差,而变宽度滑动窗口效果相对较好。拟合多项式次数的增加尤其影响固定宽度滑动窗口的滤波效果。综合而言,变宽度滑动窗口S & W(P2M8)去相关滤波器较好。
2) 平滑处理可使异常幅值减少,有的(湖和冰川)信号甚至消失,降低观测的分辨率。高斯滤波的异常幅值一般与扇形滤波相差10%~30%,扇形滤波有横向拉长作用。
3) CSR/GFZ/JPL重力场模型反演的TWSC趋势相近,但CSR较好;JPL质量模型MAS/MAS_S结果也相近,但在高原西部有较大差异。重力场模型与质量模型的结果相差很大,表现为不同的信号形态分布、幅值大小,原因是质量模型的先验约束条件具有较大的不确定性,而重力模型的结果相对可靠。
4) 使用推荐的去条带滤波器(S & W P2M8)和CSR二级重力数据反演的TWSC趋势在高原西部、中南部、长江-黄河源区出现正异常,推测与湖水和地下水有关;天山地区和喜马拉雅-念青唐古拉-横断山出现负异常,与冰川消融有关;印度西北部和孟加拉盆地出现负异常,与地下水超采有关。使用高斯平滑后,TWSC趋势分辨率降低,高原北部以黄河源区以北为中心出现东西向正异常、天山负异常和印度西北部-孟加拉盆地的负异常。
致谢: 感谢CSR、GFZ、JPL提供的GRACE RL05时变重力场数据及JPL RL05M数据。
| [1] |
Farinotti D, Longuevergne L, Moholdt G, et al. Substantial Glacier Mass Loss in the Tianshan Over the Past 50 Years[J]. Nature Geosciences, 2015(8): 716-723
(  0) 0) |
| [2] |
Chambers D P. Evaluation of New GRACE Time-Variable Gravity Data Over the Ocean[J]. Geophys Res Lett, 2006, 33: L17 603 DOI:10.1029/2006GL027296
(  0) 0) |
| [3] |
Swenson S, Wahr J. Post-Processing Removal of Correlated Errors in GRACE Data[J]. Geophys Res Lett, 2006, 33: L08 402
(  0) 0) |
| [4] |
Duan X J, Guo J Y, Shum C K, et al. On the Postprocessing Removal of Correlated Errors in GRACE Temporal Gravity Field Solutions[J]. J Geod, 2009, 83: 1095-1106 DOI:10.1007/s00190-009-0327-0
(  0) 0) |
| [5] |
Jekeli C. Alternative Methods to Smooth the Earth's Gravity Field, Rep 327[R].Ohio State Univ, Columbus, 1981 http://cn.bing.com/academic/profile?id=7bce5c61afe86367e7d9d3d7c0e617cd&encoded=0&v=paper_preview&mkt=zh-cn
(  0) 0) |
| [6] |
Zhang Z Z, Chao B F, Lu Y, et al. An Effective Filtering for GRACE Time-Variable Gravity: Fan Filter[J]. Geophysical Research Letters, 2009, 36: L17 411
(  0) 0) |
| [7] |
Zhong M, Duan J B, Xu H Z, et al. Trend of China Land Water Storage Redistribution at Medi and Large-Spatial Scales in Recent Five Years by Satellite Gravity Observations[J]. Chin Sci Bull, 2008, 54(5): 816-821
(  0) 0) |
| [8] |
Matsuo K, Heki K. Time-Variable Ice Loss in Asian High Mountains from Satellite Gravimetry[J]. Earth Planet Sci Lett, 2010, 290: 30-36 DOI:10.1016/j.epsl.2009.11.053
(  0) 0) |
| [9] |
朱传东, 陆洋, 史红岭, 等. 高亚洲冰川质量变化趋势的卫星重力探测[J]. 地球物理学报, 2015, 58(3): 793-801 (Zhu Chuandong, Lu Yang, Shi Hongling, et al. Trends of Glacial Mass Changes in High Asia from Satellite Gravity Observations[J]. Chinese J Geophysics, 2015, 58(3): 793-801)
(  0) 0) |
| [10] |
刘杰, 方剑, 李红蕾, 等. 青藏高原GRACE卫星重力长期变化[J]. 地球物理学报, 2015, 58(10): 3496-3506 (Liu Jie, Fang Jian, Li Honglei, et al. Secular Variation of Gravity Anomalies Within the Tibetan Plateau Derived from GRACE Data[J]. Chinese J Geophysics, 2015, 58(10): 3496-3506 DOI:10.6038/cjg20151006)
(  0) 0) |
| [11] |
Watkins M M, Wiese D N, Yuan D N, et al. Improved Methods for Observing Earth's Time Variable Mass Distribution with GRACE Using Spherical Cap Mascons[J]. J Geophys Res:Solid Earth, 2015, 120: 2648-2671 DOI:10.1002/2014JB011547
(  0) 0) |
| [12] |
Chen Y Y, Yang K, Qin J, et al. Evaluation of AMSR-E Retrievals and GLDAS Simulations Against Observations of a Soil Moisture Network on the Central Tibetan Plateau[J]. Journal of Geophysical Research: Atmospheres, 2013, 118: 4466-4475
(  0) 0) |
| [13] |
Cheng M K, Tapley B D. Variations in the Earth's Oblateness During the Past 28 Years[J]. J Geophys Res, 2004, 109: B09 402
(  0) 0) |
| [14] |
Swenson S, Chambers D, Wahr J. Estimating Geocenter Variations from a Combination of GRACE and Ocean Model Output[J]. J Geophys Res, 2008, 113: B08 410
(  0) 0) |
| [15] |
贾路路, 汪汉胜, 相龙伟, 等. 冰川均衡调整对南极冰质量平衡监测的影响及其不确定性[J]. 地球物理学报, 2011, 54(6): 1466-1477 (Jia Lulu, Wang Hansheng, Xiang Longwei, et al. Effects of Glacial Isostatic Adjustment on the Estimate of Ice Mass Balance Over Antarctica and the Uncertainties[J]. Chinese J Geophys, 2011, 54(6): 1466-1477 DOI:10.3969/j.issn.0001-5733.2011.06.006)
(  0) 0) |
| [16] |
Geruo A, Wahr J, Zhong S J. Computations of the Viscoelastic Response of a 3-D Compressible Earth to Surface Loading: An Application to Glacial Isostatic Adjustment in Antarctica and Canada[J]. Geophys J Int, 2013, 192: 557-572
(  0) 0) |
| [17] |
Wahr J, Molenaar M, Bryan F. Time Variability of the Earth's Gravity Field:Hydrological and Oceanic Effects and Their Possible Detection Using GRACE[J]. J Geophys Res, 1998, 103(B12): 30205-30229 DOI:10.1029/98JB02844
(  0) 0) |
| [18] |
Klees R, Zapreeva E A, Winsemius H C, et al. The Bias in GRACE Estimates of Continental Water Storage Variations[J]. Hydrol Earth Syst Sci, 2007(11): 1227-1241
(  0) 0) |
| [19] |
Rodell M, Houser P R, Jambor U, et al. The Global Land Data Assimilation System[J]. Amer Meteorol Soc, 2004, 85(3): 381-394 DOI:10.1175/BAMS-85-3-381
(  0) 0) |
| [20] |
Oleson K W, Lawrence D M, Gordon B, et al. Technical Description of Version 4.0 of the Community Land Model (CLM)[R]. National Center for Atmospheric Research, Boulder, 2010 http://cn.bing.com/academic/profile?id=13fdf007f31195d0b130b97d35a5670a&encoded=0&v=paper_preview&mkt=zh-cn
(  0) 0) |
| [21] |
Wang H S, Patrick P, Wang Z Y. An Approach for Spherical Harmonic Analysis of Non-Smooth Data[J]. Computers & Geosciences, 2006, 32(10): 1654-1668
(  0) 0) |
| [22] |
Adler R F, Huffman G J, Chang A, et al. The Version 2 Global Precipitation Climatology Project (GPCP) Monthly Precipitation Analysis (1979-Present)[J]. J Hydrometeor, 2003(4): 1147-1167
(  0) 0) |
| [23] |
Gardner A S, Moholdt G, Graham C J, et al. A Reconciled Estimate of Glacier Contributions to Sea Level Rise: 2003 to 2009[J]. Science, 2013, 340: 852-857 DOI:10.1126/science.1234532
(  0) 0) |
| [24] |
Zhang G Q, Xie H J, Kang S C, et al. Monitoring Lake Level Changes on the Tibetan Plateau Using ICESat Altimetry Data (2003-2009)[J]. Remote Sens Environ, 2011, 115(7): 1733-1742
(  0) 0) |
| [25] |
孙文科, 长谷川崇, 张新林, 等. 高斯滤波在处理GRACE数据中的模拟研究:西藏拉萨的重力变化率[J]. 中国科学, 2011, 41(9): 1327-1333 (Sun Wenke, Hasegawa T, Zhang Xinlin, et al. Effects of Gaussian Filter in Processing GRACE Data: Gravity Rate of Change at Lhasa, Southern Tibet[J]. Sci China Earth Sci, 2011, 41(9): 1327-1333)
(  0) 0) |
2. University of Chinese Academy of Sciences, A19 Yuquan Road, Beijing 100049, China;
3. National Earthquake Infrastructure Service, 56 Sanlihe Road, Beijing 100036, China
 2017, Vol. 37
2017, Vol. 37

