2. 信息工程大学导航与空天目标工程学院,郑州市科学大道62号,450001;
3. 北斗导航应用技术河南省协同创新中心,郑州市科学大道62号,450001;
4. 西安测绘研究所,西安市雁塔路中段1号,710054
影响卫星钟差预报精度的因素很多,包括原子钟的物理特性、卫星钟差的数据质量、数据的采样长度等。其中,原子钟自身的物理特性是最重要的影响因素[1]。常见的卫星钟差预报模型包括多项式预报模型、灰色模型、求和自回归滑动平均模型等[2-6]。郭海荣[7]利用幂谱噪声模型,对GPS星载原子钟的噪声变化规律进行分析;Kenneth[8]对GPS星载原子钟的周期项特性进行研究;黄观文等[9]利用频谱分析方法,对GPS钟差序列的周期项进行建模和预报;王彬等[10]基于武汉大学的精密钟差产品,对BDS在轨卫星的各项性能进行系统评估[10]。这些研究大多集中于GPS系统,对BDS系统星载钟的时频特性分析及预报的相关研究仍不充分。值得一提的是,由于我国硬件水平相对落后,BDS卫星上配备的国产铷钟的频率稳定性和精度水平相对较差。因此,有必要在探讨BDS星载钟时频特性的基础上,进一步提高BDS星载钟的预报精度。
近年来,随着北斗卫星导航系统的发展,信息工程大学、西安测绘研究所、武汉大学等机构开始研究和发布GNSS卫星轨道和钟差产品,为研究北斗卫星钟差建立了数据基础[10-12]。郑康等[13]对西安测绘研究所BDS精密轨道和钟差的精密定位性能进行研究,进一步验证了西安测绘研究所iGMAS分析中心提供的钟差产品的正确性。本文基于西安测绘研究所iGMAS分析中心发布的精密卫星钟差产品,采用频谱分析方法对BDS星载原子钟的周期项变化规律进行分析,构建附有周期项的钟差预报模型。在此基础上,对预报模型的短期预报效果进行验证。
1 基本理论 1.1 频谱分析对于钟差残差序列中的系统性误差,本文通过快速傅立叶级数展开式计算序列中各数值的频谱值:
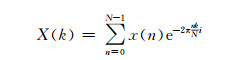
|
(1) |
式中,X(k)为k时段频谱值,x(n)为时间序列值。然后,通过序列的频谱图确定包含的显著周期项。利用快速傅立叶级数展开时,需要将序列的个数满足2的n次幂,以改善波形结构。对于个数不能满足要求的,通过补充零元素实现。
1.2 附有周期项的多项式模型构造多项式模型由于算法复杂程度低,且能基本反映卫星钟钟速和钟漂的物理特性,因此被广泛应用于卫星钟差预报。最常用的多项式模型为二次多项式模型,针对钟差序列x(tj),其模型表达式为:
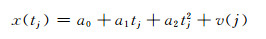
|
(2) |
式中,x(tj)表示第j个历元的卫星钟差值,tj表示第j个历元的时刻,a0、a1、a2为待估参数,v(j)为该卫星钟第j个历元钟差的残差。在式(2)基础上,考虑周期项改正的多项式模型为:
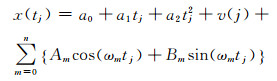
|
(3) |
式中,a0、a1、a2、Am和Bm为待求的模型参数;m=1, 2, …, n,m的大小由功率谱决定;ωk表示该卫星钟的频率变化特征参数。通过最小二乘的方法求解待估参数,并利用求解的参数进行后续的钟差预报。
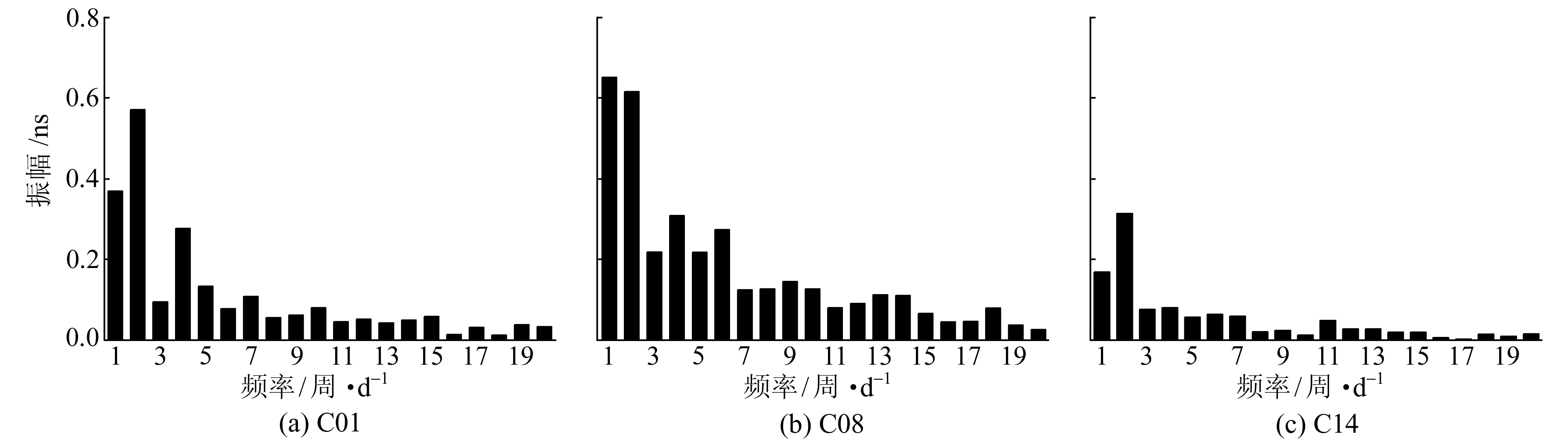
2 实验与分析 2.1 周期项特性分析采用5 min的精密卫星钟差数据验证和分析BDS卫星钟的周期特性。分别提取单颗卫星的钟差序列,对扣除二次项的拟合残差进行频谱分析,提取并分析其显著周期项。在频谱分析之前,采用MAD法对原始的钟差序列进行质量控制,消除粗差、相位跳变的不良影响[14-15]。以2015-08-01的BDS快速钟差数据作为研究对象,图 1(a)~(c)分别为3种不同轨道类型的卫星C01(GEO)、C08(IGSO)和C14(MEO)的频谱图。
|
图 1 不同轨道类型卫星的频谱图 Fig. 1 Spectral analysis of different types of satellites |
可以看出,3种不同轨道类型的卫星表现出相近的显著周期项特征,但其对应的能量幅值存在差异。主要存在12 h(频率等于2)、8 h(频率等于3)以及24 h(频率等于1)3个显著周期项,而48 h(频率等于5)及后续小周期项变化幅值较小。
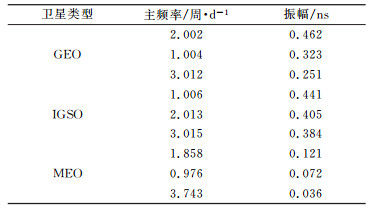
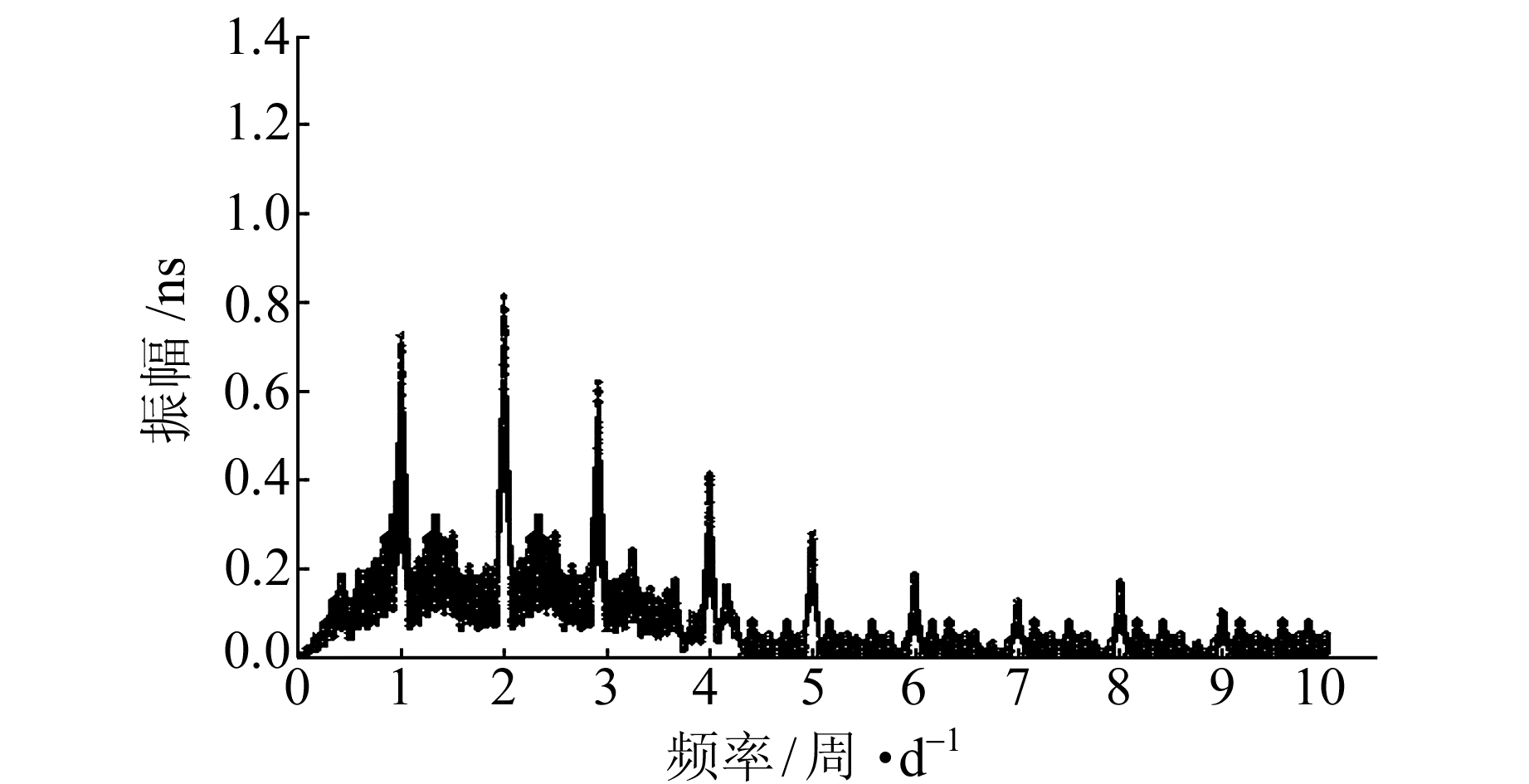
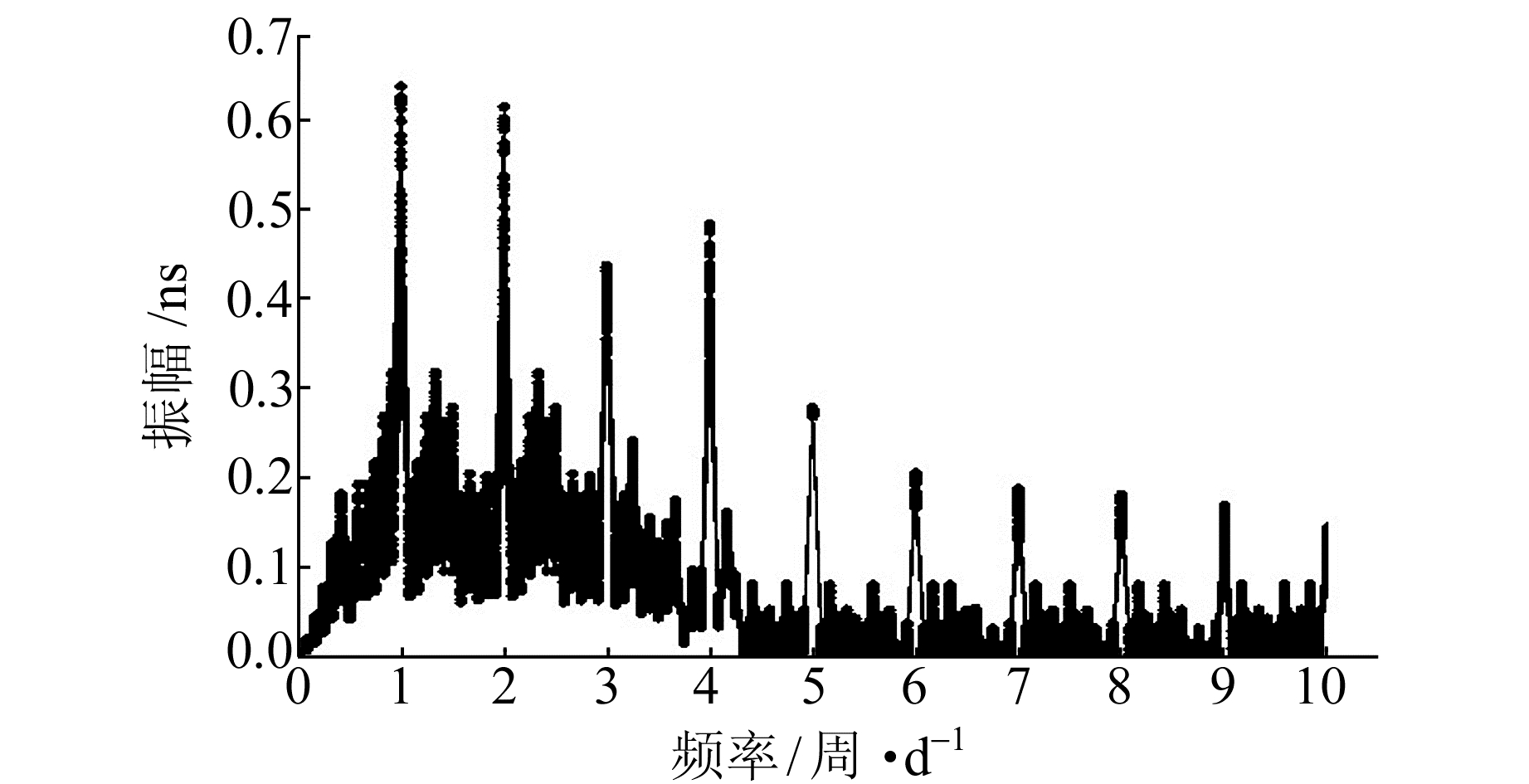
为了进一步分析BDS星载钟在较长时间内的周期项变化规律,采用2015年连续2个月(08-01~09-30)的快速钟差产品,去掉质量较差的数据,对剩余53 d数据的逐日拟合残差进行周期项分析,图 2~4给出了GEO、IGSO和MEO 3种不同类型星载原子钟的频谱序列图,表 1给出经过谱分析得到的主频率统计结果。
|
图 2 GEO卫星的能量谱示意图 Fig. 2 Spectral analysis of GEO satellites |
|
图 3 IGSO卫星的能量谱示意图 Fig. 3 Spectral analysis of IGSO satellites |

|
图 4 MEO卫星的能量谱示意图 Fig. 4 Spectral analysis of MEO satellites |
|
|
表 1 北斗卫星钟差谱分析结果 Tab. 1 Results of spectral analysis of BDS satellites |
1) 总体而言,不同类型卫星的近似12 h和24 h周期项均较为显著,且随着频率的增大,与之相对应的周期项幅值逐渐减小,与单天统计结果相一致。这与BDS卫星运行的轨道周期(GEO、IGSO近似为24 h,MEO近似为12 h)相一致,说明BDS卫星钟的主显著周期项可能由卫星的轨道周期所决定。
2) MEO卫星不同周期项的能量幅值较GEO、IGSO卫星均有较大幅度的降低,这可能是由于MEO卫星的定轨精度高于GEO和IGSO卫星,从而轨道中未模型化的误差较小的缘故。由于卫星轨道和钟差存在耦合关系,因此在精密钟差中周期项的振幅较小。
3) 就显著周期项的分布而言,GEO卫星的周期项从大至小依次为近似12 h、24 h、8 h、6 h周期;IGSO卫星的近似24 h周期项最为显著,略大于12 h周期项;而MEO卫星的主显著周期项为近似12 h,其次为24 h,剩余周期项的变化幅值不显著。GEO卫星周期项存在的原因及其物理特性有待进一步研究。
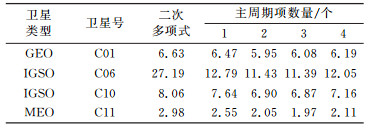
2.2 卫星钟差预报分析 2.2.1 主周期项改正数目的影响分析改正周期项的数目由功率谱决定,一般选择前1~3个主周期项进行改进。为了验证选择的周期项数目对预报精度的影响,采用1 d的精密钟差产品进行实验。分别采用前1~4个功率谱频率作为周期项构建预报模型,预报后续24 h的卫星钟差,并将预报结果与实测精密钟差进行对比。选择C01、C06、C10、C11进行分析,不同改正模型的精度结果见表 2(单位ns)。
|
|
表 2 BDS不同类型卫星采用不同模型的预报精度 Tab. 2 Results of BDS prediction error by using different models |
从表 2可以看出,同未加入周期项改正相比,加入周期项改正的预报精度明显提高,这也进一步验证了卫星钟差周期性变化的存在。值得注意的是,引入2~3个主要周期项的精度改进幅度较高,若继续增加周期项,其精度的改进幅度不显著,甚至会出现一定程度的减小。
2.2.2 预报精度分析基于上文结论,选择前3个功率谱对应的频率构造附有周期项的多项式预报模型。采用参数估计的方法求解模型参数,并利用求解的参数实现后续历元的钟差预报。限于篇幅,本文仅以2015-08-01~08-21共3周的快速钟差数据为例,分析模型的预报精度。由于C13卫星在采用的数据时段内未提供服务,本文及后续实验未涉及对该颗卫星的分析。
为了分析附有周期项的多项式模型的改进效果,采用1 d的数据作为历史数据进行逐日拟合,对传统的二次多项式模型和附有周期项的预报模型的拟合和预报精度进行对比,见图 5、图 6。

|
图 5 BDS卫星二次项拟合残差序列 Fig. 5 Quadratic Fitting errors for BDS satellites |
|
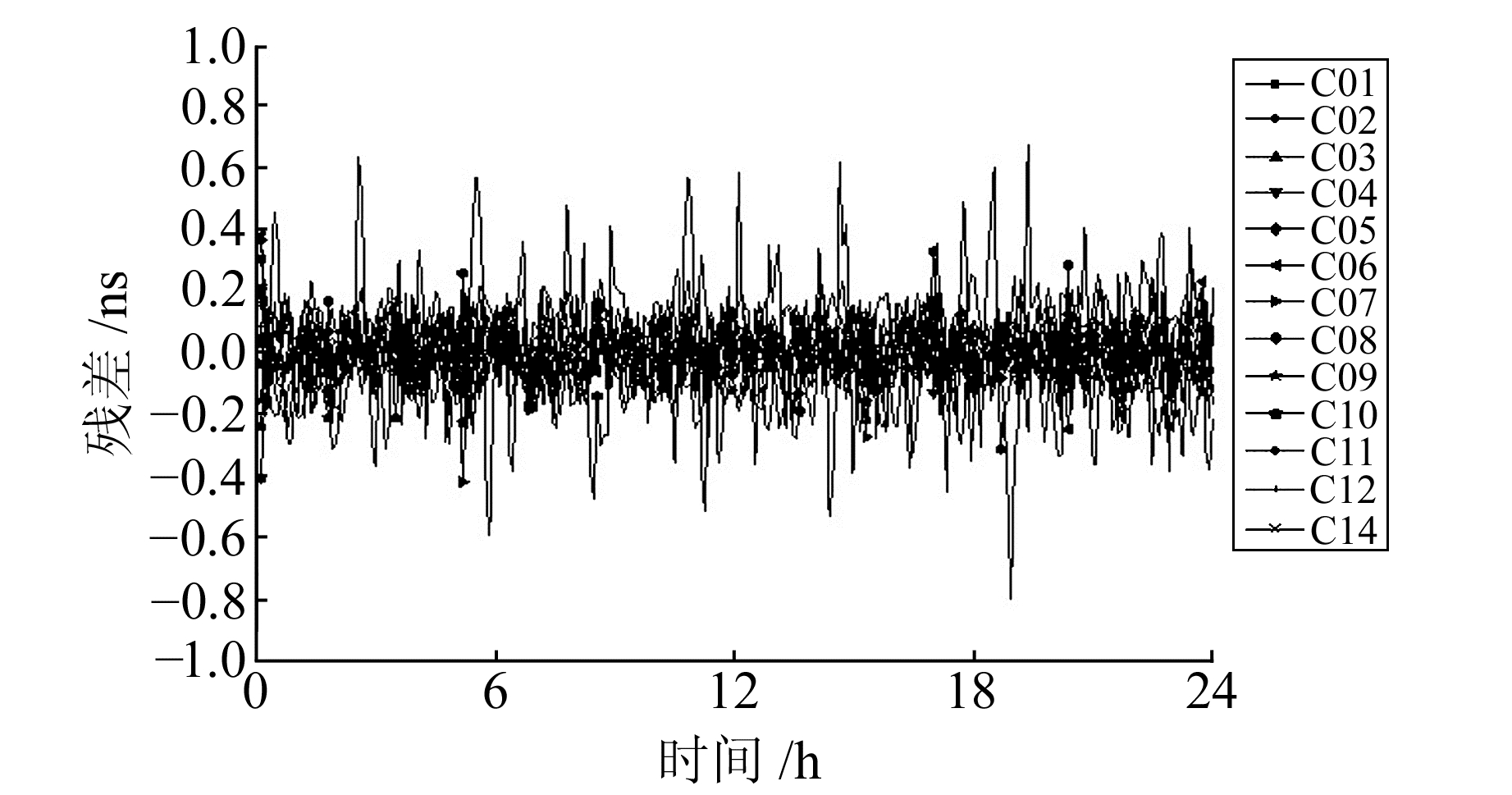
图 6 BDS卫星应用改进模型的拟合残差序列 Fig. 6 Fitting errors for BDS satellites using improved model |
从图 5可以看出,几乎所有卫星的二次项残差均表现出一定的周期特性,从残差序列图中也可直观地看出其基本符合12 h和24 h的显著周期项变化规律。此外,不同星载原子钟的残差特性存在较大差异,其中C06、C08的拟合精度明显较差。通过图 6可以得到结论,排除显著周期项影响后的拟合残差序列精度得到明显改善,不同卫星的拟合残差均不超过1 ns。但值得关注的是,对于稳定性较差的卫星,其拟合残差仍然较大。
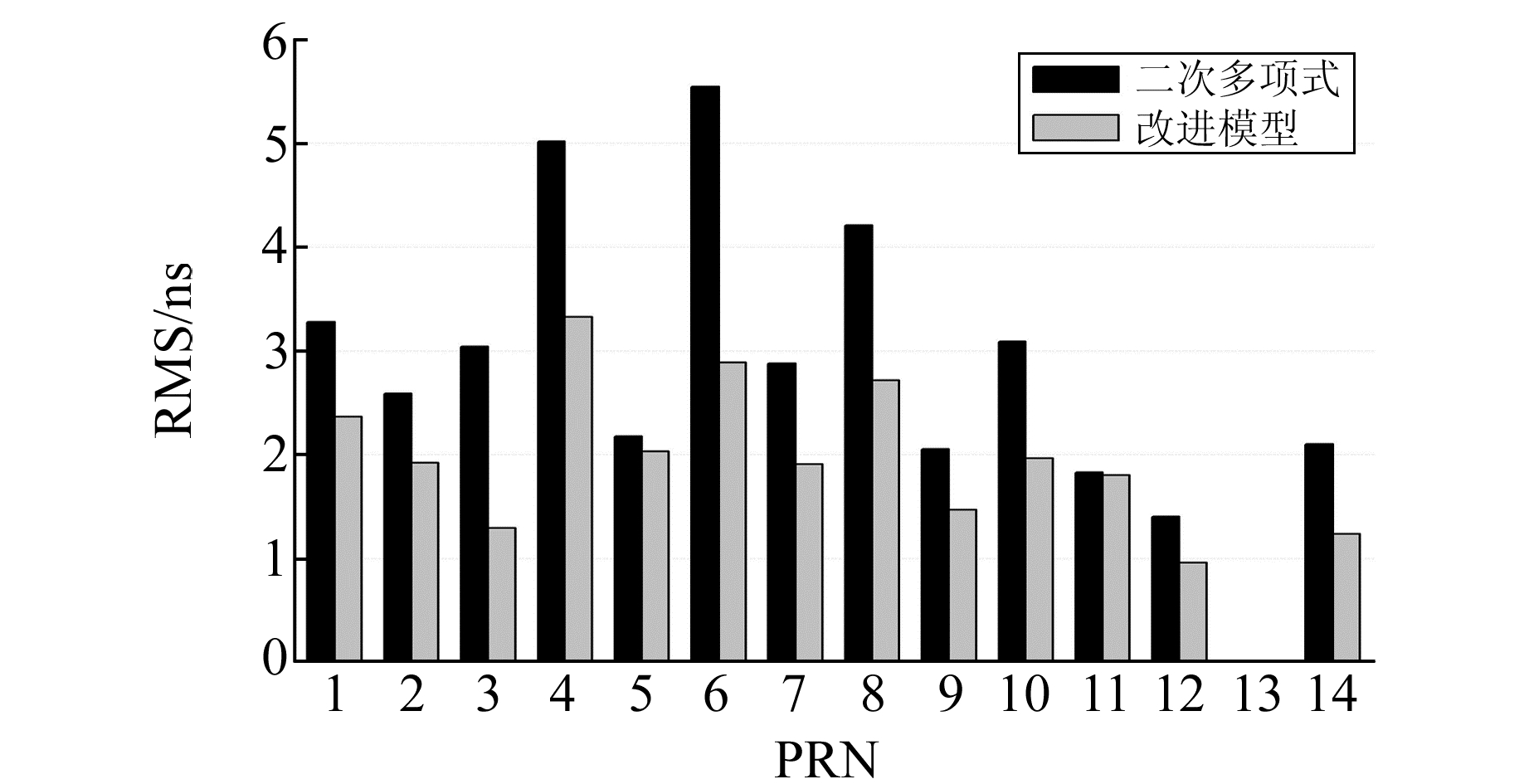
利用模型的拟合残差进行预报,以实测钟差作为基准,计算并统计预报钟差与基准之间的均方根误差,并以此作为预报精度的评估依据。6 h、12 h、24 h的预报结果见图 7~9,图中的预报精度为利用3周数据计算的平均统计结果。
|
图 7 6 h预报精度统计 Fig. 7 6 h prediction errors with different model |

|
图 8 12 h预报精度统计 Fig. 8 12 h prediction errors with different model |

|
图 9 24 h预报精度统计 Fig. 9 24 h prediction errors with different model |
总体而言,经过周期项修正后的预报模型的预报精度优于传统模型,附有周期项的预报模型的6 h预报精度在2 ns左右,24 h的预报精度在10 ns左右,均优于采用常规模型。为了对不同轨道类型的星载原子钟的预报效果进行分析,对不同类型的星载原子钟进行分类,并统计在不同预报时长下的预报精度和模型改正率。模型改正率Perc的计算方法如下:
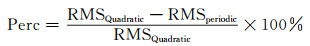
|
(4) |
不同类型卫星的预报精度统计见表 3。可以看出,随着预报时间的延长,两种预报模型均存在着一定的误差积累。北斗MEO卫星的预报精度最高,6 h的预报精度优于2 ns,24 h的预报精度优于5 ns。而IGSO卫星与GEO卫星的预报精度相对较低。总体而言,改进模型的平均改进幅度在20%~40%。由于MEO卫星不同周期项的能量幅值较低,从改进幅度而言,GEO、IGSO卫星的改进幅度略大于MEO卫星。关于模型改正率的影响因素有待进一步研究。
|
|
表 3 不同类型卫星的预报精度 Tab. 3 Prediction errors of different types of satellites |
本文在对BDS星载原子钟的周期项变化分析的基础上,构建了附有周期项的钟差预报模型。在此基础上对预报模型的短期预报效果进行验证, 得到以下结论:
1) BDS不同类型的卫星均表现出较为显著的12 h和24 h周期项变化规律,但其对应的能量幅值存在差异,MEO卫星不同周期项的能量幅值较GEO、IGSO卫星有大幅度的降低。
2) 排除显著周期项影响后的拟合残差序列精度得到明显改善,不同卫星的拟合残差均不超过1 ns。但值得关注的是,对于稳定性较差的卫星,其拟合残差仍然较大。
3) 结合周期项改正的钟差预报模型能够较为显著地提高预报精度,6 h的预报精度在2 ns左右,24 h的预报精度在10 ns左右。其中MEO卫星的预报精度高于GEO和IGSO卫星,而IGSO卫星的精度提高较为明显。
| [1] |
唐桂芬, 许雪晴, 曹纪东, 等. 基于通用钟差模型的北斗钟预报精度分析[J]. 中国科学:物理学力学天文学, 2015, 45(7): 1-6 (Tang Guifen, Xu Xueqing, Cao Jidong, et al. Precision Analysis for Compass Satellite Clock Prediction Based on a Universal Clock Offset Model[J]. Scientia Sinica:Phyisca, Mechanica&Astronomica, 2015, 45(7): 1-6)
(  0) 0) |
| [2] |
付文举.GNSS在轨卫星钟特性分析及钟差预报研究[D].西安: 长安大学, 2014 (Fu Wenju.Research on Prediction and Characteristics of Satellite Clock on Orbit[D].Xi'an: Chang'an University, 2014) http://cdmd.cnki.com.cn/Article/CDMD-10710-1014070907.htm
(  0) 0) |
| [3] |
郑作亚, 党亚民, 卢秀山, 等. 附有周期项的预报模型及其在GPS卫星钟差预报中的应用研究[J]. 天文学报, 2010, 51(1): 95-102 (Zheng Zuoya, Dang Yamin, Lu Xiushan, et al. Prediction Model with Periodic Item and Its Application to the Prediction of GPS Satellite Clock Bias[J]. Acta Astronomica Sinina, 2010, 51(1): 95-102)
(  0) 0) |
| [4] |
黄观文, 张勤, 许国昌, 等. 基于频谱分析的IGS精密星历卫星钟差精度分析研究[J]. 武汉大学学报:信息科学版, 2008, 33(5): 497-499 (Huang Guanwen, Zhang Qin, Xu Guochang, et al. IGS Precise Satellite Clock Model Fitting and Its Precision by Using Sprctral Analysis Method[J]. Geomatics and Information Science of Wuhan University, 2008, 33(5): 497-499)
(  0) 0) |
| [5] |
范旭亮, 王晓红, 张显云, 等. 基于ARIMA模型的卫星钟差短期预报研究[J]. 测绘与空间地理信息, 2015, 38(1): 105-110 (Fan Xuliang, Wang Xiaohong, Zhang Xianyun, et al. Study on Short-Term Prediction for Satellite Clock Bias Based on ARIMA Model[J]. Geomatics & Spatial Information Technology, 2015, 38(1): 105-110)
(  0) 0) |
| [6] |
路晓峰, 贾小林, 崔先强. 灰色系统理论的优化方法及其在卫星钟差短期预报中的应用[J]. 测绘工程, 2006, 15(6): 12-14 (Lu Xiaofeng, Jia Xiaolin, Cui Xianqiang. The Optimization Method of Gray System Theory for the Satellite Clock Error Short-Term Predicting[J]. Engineering of Surveying and Mapping, 2006, 15(6): 12-14 DOI:10.3969/j.issn.1006-7949.2006.06.004)
(  0) 0) |
| [7] |
郭海荣.导航卫星原子钟时频特性分析理论与方法研究[D].郑州: 信息工程大学, 2006 (Guo Hairong.Study on the Analysis Theories and Algorithms of the Time and Frequency Characterization for Atomic Clocks of Navigation Satellites[D].Zhengzhou: Information Engineering University, 2006) http://cdmd.cnki.com.cn/article/cdmd-90008-2007051629.htm
(  0) 0) |
| [8] |
Kenneth L S, Jim R R, Ronald L B. Characterization of Periodic Variations in the GPS Satellite Clocks[J]. GPS Solution, 2008, 12: 211-225 DOI:10.1007/s10291-008-0089-9
(  0) 0) |
| [9] |
黄观文.GNSS星载原子钟质量评价及精密钟差算法研究[D].西安: 长安大学, 2012 (Huang Guanwen.Research on Algorithms of Precise Clock Offset and Quality Evaluation of GNSS Satellite Clock[D]. Xi'an: Chang'an University, 2012) http://cdmd.cnki.com.cn/Article/CDMD-10710-1013017231.htm
(  0) 0) |
| [10] |
Wang B, Lou Y, Liu J, et al. Analysis of BDS Satellite Clocks in Orbit[J]. GPS Solution, 2015, 9(15): 1-12
(  0) 0) |
| [11] |
刘伟平, 郝金明, 李建文, 等. 多GNSS融合的北斗卫星精密定轨[J]. 测绘学报, 2014, 43(11): 1132-1138 (Liu Weiping, Hao Jinming, Li Jianwen, et al. Multi-GNSS Joint Precise Orbit Determination of Beidou Navigation Satellite System[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(11): 1132-1138)
(  0) 0) |
| [12] |
朱永兴, 冯来平, 贾小林, 等. 北斗区域导航系统的PPP精度分析[J]. 测绘学报, 2015, 44(4): 377-383 (Zhu Yongxing, Feng Laiping, Jia Xiaolin, et al. The PPP Precision Analysis Based on BDS Regional Navigation System[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(4): 377-383)
(  0) 0) |
| [13] |
郑康, 阮仁桂, 贾小林. GNSS精密单点定位精度分析[J]. 测绘科学与工程, 2015, 35(6): 21-25 (Zheng Kang, Ruan Rengui, Jia Xiaolin. Accuracy Analysis of GNSS Precise Point Positioning[J]. Geomatics Science and Engineering, 2015, 35(6): 21-25)
(  0) 0) |
| [14] |
Riley W J. Frequency Jump Detection in Stable32[M]. Beaufort S C: Hamiltion Technical Services, 2008
(  0) 0) |
| [15] |
Bartoccini U, Barchi G, Nunzi E.Methods and Tools for Frequency Jump Detection[C].IEEE International Workshop on Advanced Methods for Uncertainty Estimation in Measurement, 2009 https://www.researchgate.net/publication/251895351_Methods_and_tools_for_frequency_jump_detection
(  0) 0) |
2. School of Navigation and Aerospace Engineering, Information Engineering University, 62 Kexue Road, Zhengzhou 450001, China;
3. Beidou Navigation Technology Collaborative Innovation Center of Henan, 62 Kexue Road, Zhengzhou 450001, China;
4. Xi'an Institute of Surveying and Mapping, 1 Mid-Yanta Road, Xi'an 710054, China
 2017, Vol. 37
2017, Vol. 37