GNSS多模解算可充分利用各系统的优势,改善卫星几何构型,提高导航定位的精度和可靠性[1-3]。北斗卫星导航系统(BDS)是我国自主发展、独立运营的卫星导航定位系统,目前拥有工作卫星14颗,其中GEO卫星5颗、IGSO卫星5颗、MEO卫星4颗,具备覆盖亚太地区的定位、导航、授时及短报文通信服务能力[4-7]。研究表明,GPS与BDS基线解算结果之间存在系统偏差,导致联合解算结果与单模解算结果之间具有系统性差异[8-10]。如施闯[8]等在436 m基线上利用PANDA软件通过BDS单历元相位差分解算得到的基线分量日均值与GPS解算结果相差3 cm左右;利用PANDA软件的静态基线解算功能得到的BDS基线分量周均值与GPS相比在E、N、U方向上的差异分别为6.2 mm、0.7 mm、-5.0 mm,并推测此系统差可能由接收天线北斗信号相位中心偏差引起[9]。系统偏差的存在破坏了BDS与其他GNSS系统之间的兼容性与互操作性,如何解释并消除此系统偏差,是目前我国北斗卫星导航系统亟待解决的一个问题。
本文从BDS数据解算的函数模型出发,推导了天线相位中心偏差对基线解算结果的影响方式,研究了GPS/BDS系统偏差中天线相位中心偏差所起的作用,并利用实测数据对理论推导结果进行验证,对于促进BDS在高精度导航定位领域的应用具有一定的意义。
1 天线相位中心改正对基线解算的影响天线相位中心改正直接在坐标域内影响解算结果,对提高BDS导航定位精度具有重要意义。天线相位中心改正包括卫星天线相位中心改正和接收天线相位中心改正,一般采用绝对天线相位中心改正模型[11]。其由两部分组成:相对于天线参考点(antenna reference point, ARP)的平均相位中心偏差(phase center offset, PCO);相对于平均相位中心(average phase center, APC)随入射信号高度角和方位角改变的瞬时相位中心变化[12-14](phase center variation, PCV)。PCV改正一般在mm级,本文主要讨论PCO改正对解算结果的影响。
1.1 卫星天线相位中心改正对基线结果的影响卫星天线相位中心的PCO改正随卫星类型及卫星号的不同而不同,与每颗卫星的制造工艺相关。GPS系统卫星的PCO改正在0.8 m~2.9 m之间,其中BLOCKⅡR-M卫星的PCO改正较小,在0.8 m左右。本文中BDS系统卫星的PCO改正采用MGEX(Multi-GNSS Experiment)推荐的模型,改正量约1 m。忽略卫星的PCO改正会使这些误差被吸收到轨道中。轨道误差对基线解算的影响可用式(1)估计[15]:
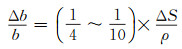
|
(1) |
式中, Δb为卫星星历误差所引起的基线偏差;b为基线长度;ΔS为轨道误差;ρ为卫星与地面距离。(
接收天线相位中心改正直接影响解算结果,是GNSS数据处理中的重要问题。在GNSS数据解算的观测方程中,接收天线相位中心在观测瞬间的位置可表示为[17]:
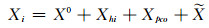
|
(2) |
其中, Xi为信号接收时刻接收天线相位中心的位置;X0为测站标志中心近似位置;Xhi为天线高;Xpco为接收天线相位中心改正;
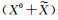
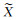
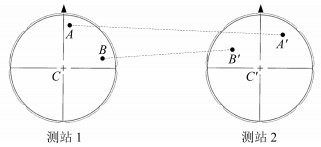
数据解算时,基线解是利用式(2)所得的测站坐标作差获得的。由式(2)可知,在天线严格指北的情况下,若基线两端接收天线均不进行相位中心改正,则基线结果是两接收天线平均相位中心APC之间的矢量;若两天线均施加相位中心改正,则基线结果是两天线ARP参考点之间的矢量。由于目前绝大部分接收天线GPS信号的相位中心已有相应的改正模型,而BDS信号的相位中心偏差还无法准确获知,因此当基线两端天线类型不同时,若GPS信号施加了相位中心改正,而BDS信号没有施加时,两系统所得基线结果之间将存在一系统偏差。若GPS解算与BDS解算均不施加相位中心改正,则两系统基线结果之间同样存在系统偏差。如图 1所示,A、A′为GPS测量的平均相位中心;B、B′为BDS测量的平均相位中心;C、C′为两接收天线的ARP参考点。若不施加接收天线相位中心改正,则GPS解算结果为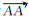
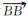
|
图 1 天线类型不同引起的GPS/BDS系统偏差 Fig. 1 Systematic deviation between GPS and BDS caused by different antenna types |
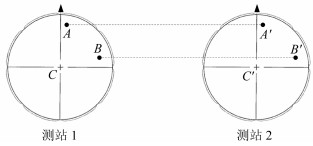
若基线两端天线类型相同且均严格指北,则两天线平均相位中心之间的矢量与两天线ARP参考点之间的矢量一致,如图 2所示,图中标志含义与图 1相同,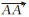
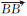
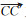
|
图 2 天线类型相同时相位中心偏差的影响 Fig. 2 Influence of antenna phase center offsets when using the same type of antenna |
若基线两端接收天线类型相同且严格水平,但二者指向不同,则GPS与BDS基线结果之间同样存在由天线相位中心偏差所引起的系统误差。此系统误差的大小由各系统天线相位中心改正的大小及天线指向的偏转角度决定。因PCO改正在水平方向的分量通常较小,故此误差一般为mm级。由接收天线未严格水平所引起的系统偏差与水平情况类似,不再赘述。需注意的是,因PCO改正高程分量通常较大(部分类型天线垂向方向PCO改正达10 cm),由此引起的系统偏差较为显著,外业测量时需注意避免此情况发生。
2 数据分析 2.1 数据采集为研究GPS/BDS解算中天线相位中心偏差的影响,本文通过实测数据对理论推导结果进行验证。
实验在中国中部某城市进行。采用的接收机为Trimble NetR9型,可同时接收GPS与BDS信号。为分析天线类型不同所引起的系统偏差,采用两类接收天线:TRM29659.00,TRM55971.00。实验共布设3个测站(WD01、WD02、ZKWS),各测站配备的仪器设备见表 1,站间基线长度见表 2。
|
|
表 1 各测站仪器类型 Tab. 1 Summary of equipments installed at each site |
|
|
表 2 测站间基线长度 Tab. 2 Length of each baseline |
本次实验共采集2014-07-05(年积日186)12:00~16:00(北京时间)4 h的数据。采样间隔15 s,截止高度角10°。数据通过静态测量方法得到。数据采集过程中,所有接收天线均置水平且严格指北。
2.2 结果分析为验证上述理论结果,本文设计3个实验:
1) 在施加与不施加接收天线PCV改正的条件下分别进行GPS解算,以分析PCV改正对基线结果的影响;
2) 忽略PCV改正的影响,在施加与不施加接收天线PCO改正的条件下分别进行GPS解算,分析基线结果差异;
3) 以上述实验结论为基础,在施加与不施加接收天线PCO改正的条件下分别进行GPS和BDS解算,以分析天线相位中心偏差对GPS/BDS系统偏差的影响。
GPS与BDS基线解算均采用DDMS软件完成。DDMS软件由武汉大学开发,目前可处理GPS与BDS数据。
表 3为施加PCO改正条件下,忽略接收天线PCV改正对GPS基线解算结果的影响。接收天线的PCV偏差通常直接在距离观测值上改正,一般在mm级,与信号高度角直接相关。由表 3可知,在本文的实验环境下,接收天线PCV改正对GPS基线结果的影响在mm级,影响大小与基线长度相关,且在高程方向较平面方向更为显著。考虑到PCV改正对基线结果的影响较小,本文下述讨论均忽略接收天线PCV改正的影响。
|
|
表 3 接收天线PCV改正对GPS基线结果的影响 Tab. 3 Influence of receiver antenna PCV corrections on GPS baselines |
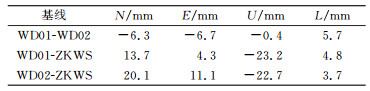
表 4为数据处理过程中两类天线所采用的相位中心PCO改正值,来源于IGS公布的天线相位中心改正模型。表 5为施加PCO改正前后GPS基线结果中各分量较差。基线解算时固定WD01站,其余测站松约束。由表 5可知,基线两端天线类型相同时,是否施加相位中心PCO改正对基线结果无影响,基线各分量较差均为0。基线两端天线类型不同时,基线结果各分量存在明显较差,且此较差与两类天线相位中心PCO改正之差基本相等(1.13 mm,0.72 mm,-24.78 mm)。
|
|
表 4 GPS L1频率PCO改正值 Tab. 4 PCO corrections for GPS L1 signals |
|
|
表 5 施加PCO改正前后GPS基线结果各分量较差 Tab. 5 Difference of GPS baseline components before and after imposing PCO corrections |
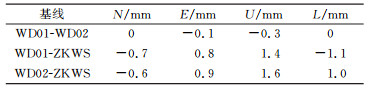
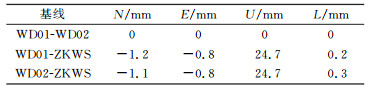
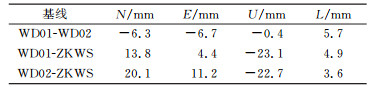
表 6、表 7为GPS与BDS解算结果对应的基线分量的较差。其中表 6中所有测站均不施加PCO改正;表 7中GPS与BDS结果全部施加了PCO改正。BDS采用GPS所对应的改正值,以近似天线相位中心偏差对BDS解算结果的影响。比较表 6、7的结果可知,由于本实验中GPS和BDS采用相同的PCO改正值,因此是否施加PCO改正对基线结果并无太大影响,二者对应基线分量的较差小于0.1 mm。表 8为表 6、7中对应基线分量较差的标准差。在计算较差标准差时,认为不同系统对应的基线分量之间不相关。本实验在数据采集时所有接收天线均水平且严格指北,从而消除天线指向对基线结果的影响。在解算过程中,两系统均固定ZKWS站,给予其余测站100 m松约束。结合表 6~8可知,在本文的实验条件下,GPS与BDS解算结果对应基线分量之间较差明显,且此较差远大于标准差,WD01-WD02基线之间较差为mm级,WD01-ZKWS基线以及WD02-ZKWS基线之间较差达1~2 cm。由表 1、5可知,WD01-ZKWS基线以及WD02-ZKWS基线两端天线类型不同,故较差中存在天线相位中心改正模型差异的影响。但此差异在垂直方向较显著,水平方向不同类型天线PCO改正差异一般在mm级(见表 4)。表 6、7中基线两端天线类型不同时两系统水平分量的较差达1~2 cm,故推测此较差并非源于不同类型天线相位中心改正模型的差异。WD01-WD02基线两端采用相同的接收设备,且在数据采集、处理过程中已采取多种策略消除各类误差影响,但在基线结果中仍存在6 mm左右的系统偏差,说明本实验中GPS与BDS基线结果中的系统偏差并非完全源于接收天线相位中心偏差,其原因仍需进一步研究和分析。
|
|
表 6 GPS与BDS对应基线分量较差(不施加PCO改正) Tab. 6 Difference of baseline components between GPS and BDS (without PCO corrections) |
|
|
表 7 GPS与BDS对应基线分量较差(施加PCO改正) Tab. 7 Difference of baseline components between GPS and BDS (with PCO corrections) |
|
|
表 8 GPS与BDS对应基线分量较差的标准差 Tab. 8 Standard deviations of baseline components difference between GPS and BDS |
本文研究了GPS和BDS基线结果中天线相位中心改正的影响,得到如下结论:
1) GPS与BDS解算结果之间确实存在系统偏差。对于2 km左右的基线,偏差达1~2 cm。
2) 天线相位中心偏差可引起GPS与BDS基线解算结果之间的系统偏差,但此偏差量级较小,水平方向一般在mm级。
3) 在消除相位中心偏差影响后,GPS与BDS基线结果之间的偏差依然存在。
GPS和BDS基线结果中的系统偏差破坏了GNSS各系统之间的兼容性和互操作性,阻碍了BDS与其他GNSS联合多模高精度解算的可能。尽快查明此系统偏差产生的原因并发展可靠的解决方案,对于拓展我国北斗卫星导航系统的应用空间具有重要意义。
| [1] |
Feng Y M. Combined Galileo and GPS:A Technical Perspective[J]. Journal of Global Positioning Systems, 2003, 2(1): 67-72 DOI:10.5081/jgps
(  0) 0) |
| [2] |
Zaidi A S, Suddle M R.Global Navigation Satellite Systems: A Survey[C].2006 International Conference on IEEE, 2006 https://www.researchgate.net/publication/224057285_Global_Navigation_Satellite_Systems_A_Survey
(  0) 0) |
| [3] |
Odolinski R, Teunissen P J G, Odijk D. Combined BDS, Galileo, QZSS and GPS Single-Frequency RTK[J]. GPS Solutions, 2015, 19(1): 151-163 DOI:10.1007/s10291-014-0376-6
(  0) 0) |
| [4] |
杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1): 1-6 (Yang Yuanxi. Progress, Contribution and Challenges of Compass/Beidou Satellite Navigation System[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 1-6)
(  0) 0) |
| [5] |
Steigenberger P, Hugentobler U, Hauschild A, et al. Orbit and Clock Analysis of Compass GEO and IGSO Satellites[J]. Journal of Geodesy, 2013, 87(6): 515-525 DOI:10.1007/s00190-013-0625-4
(  0) 0) |
| [6] |
Zhao Q L, Guo J, Li M, et al. Initial Results of Precise Orbit and Clock Determination for COMPASS Navigation Satellite System[J]. Journal of Geodesy, 2013, 87(5): 475-486 DOI:10.1007/s00190-013-0622-7
(  0) 0) |
| [7] |
中国卫星导航系统管理办公室.北斗卫星导航系统空间信号接口控制文件2.0[EB/OL].http://www.beidou.gov.cn,2013-12-27 (China Satellite Navigation Office.Beidou Navigation Satellite System Signal in Space Interface Control Document 2.0[EB/OL].http://www.beidou.gov.cn,2013-12-27)
(  0) 0) |
| [8] |
Shi C, Zhao Q L, Hu Z G, et al. Precise Relative Positioning Using Real Tracking Data from COMPASS GEO and IGSO Satellites[J]. GPS Solutions, 2013, 17(1): 103-119 DOI:10.1007/s10291-012-0264-x
(  0) 0) |
| [9] |
施闯, 赵齐乐, 李敏, 等. 北斗卫星导航系统的精密定轨和定位研究[J]. 中国科学:地球科学, 2012, 42(6): 854-861 (Shi Chuang, Zhao Qile, Li Min, et al. Precise Orbit Determination of Beidou Satellites with Precise Positioning[J]. Science China:Earth Sciences, 2012, 42(6): 854-861)
(  0) 0) |
| [10] |
He H B, Li J L, Yang Y X, et al. Performance Assessment of Single-and Dual-Frequency Beidou/GPS Single-Epoch Kinematic Positioning[J]. GPS Solutions, 2014, 18(3): 393-403 DOI:10.1007/s10291-013-0339-3
(  0) 0) |
| [11] |
杨凯, 刘鸿飞, 赵倩, 等. 绝对天线相位改正模型对GPS精密数据处理的影响[J]. 武汉大学学报:信息科学版, 2010, 35(6): 694-697 (Yang Kai, Liu Hongfei, Zhao Qian, et al. Influence of Absolute Antenna Corrections on GPS Precise Positioning[J]. Geomatics and Information Science of Wuhan University, 2010, 35(6): 694-697)
(  0) 0) |
| [12] |
Schmid R, Rothacher M, Thaller D, et al. Absolute Phase Center Corrections of Satellite and Receiver Antennas[J]. GPS Solutions, 2005, 9(4): 283-293 DOI:10.1007/s10291-005-0134-x
(  0) 0) |
| [13] |
郭际明, 史俊波, 汪伟. 天线相位中心偏移和变化对高精度GPS数据处理的影响[J]. 武汉大学学报:信息科学版, 2007, 32(12): 1143-1146 (Guo Jiming, Shi Junbo, Wang Wei. Impact of Antenna Phase Center Offset and Variation for High Precision GPS Data Processing[J]. Geomatics and Information Science of Wuhan University, 2007, 32(12): 1143-1146)
(  0) 0) |
| [14] |
Mader G L. GPS Antenna Calibration at the National Geodetic Survey[J]. GPS Solutions, 1999, 3(1): 50-58 DOI:10.1007/PL00012780
(  0) 0) |
| [15] |
姜卫平, 刘经南, 叶世榕. GPS形变监测网基线处理中系统误差的分析[J]. 武汉大学学报:信息科学版, 2001, 26(3): 166-169 (Jiang Weiping, Liu Jingnan, Ye Shirong. The Systematical Error Analysis of Baseline Processing in GPS Network[J]. Geomatics and Information Science of Wuhan University, 2001, 26(3): 166-169)
(  0) 0) |
| [16] |
李征航, 黄劲松. GPS测量与数据处理[M]. 武汉: 武汉大学出版社, 2010 (Li Zhenghang, Huang Jinsong. GPS Surveying and Data Processing[M]. Wuhan: Wuhan University Press, 2010)
(  0) 0) |
| [17] |
魏子卿, 葛茂荣. GPS相对定位的数学模型[M]. 北京: 测绘出版社, 1998 (Wei Ziqing, Ge Maorong. Relative Positioning Mathematics Model in Global Positioning System[M]. Beijing: Surveying and Mapping Press, 1998)
(  0) 0) |
 2017, Vol. 37
2017, Vol. 37