2. 湖南省气象局, 长沙市芙蓉南路四段196号, 410118;
3. 湖南科技大学资源环境与安全工程学院, 湘潭市桃园路, 411201
GPS气象遥感技术可从GPS信号传播延迟反演出高精度的可降水量(PWV)[1-2]。通过GPS解算的对流层天顶延迟(ZTD)分为干、湿两个延迟分量,其中干延迟(ZHD)可用地面气象资料通过公式精确算出,ZTD减去ZHD便得到湿延迟(ZWD),ZWD再乘以一个转换系数Ⅱ就可得到PWV[3]。大气加权平均温度(Tm)是求解ZWD和PWV之间转换系数Ⅱ的关键变量, 因此,高精度Tm成了影响GPS PWV精度的一个关键参数。
目前普遍使用Bevis公式来计算Tm[1], Bevis算式利用美国北纬27°~65°范围内8 718次探空站资料建立,应用到其他地区存在一定偏差[4]。国内不少学者为建立本地化Tm模型开展了大量研究。李建国等[5]应用中尺度气象模式给出了适合中国东部地区和不同季节的Tm模型;刘焱雄等[6]采用回归分析方法建立了适合香港本地的Tm最优回归方程;谷晓平等[7]利用清远探空站1996~2001年气象资料, 采用最优子集回归方法建立Tm回归算式;单九升、吕弋培、王勇等利用线性回归法分别建立了江西、成都以及武汉地区的Tm模型[8-10];朱爽[11]利用北京站2005~2010年无线电探空数据,使用最小二乘法建立北京地区的Tm本地化模型;张洛恺等[12]利用郑州无线电探空站2013年气象资料,用线性回归法得出郑州地区的单因子和多因子Tm计算模型;陈鹏等[13]利用2007~2011年NCEP再分析资料建立全球加权平均温度Tm模型;王晓英等[14]利用香港探空站2003~2009年数据分季节建立了春夏秋冬不同的Tm模型;龚绍琦[15]对全国按气候分区和季节分区分别建立了单因子和多因子Tm回归模型。
本文利用湖南省长沙、怀化、郴州3个探空站2012~2014年的探空数据建立湖南地区的本地化Tm模型,并对该模型的内符合和外符合精度进行分析,为湖南地区的地基GPS水汽遥感奠定应用基础。
1 数据处理方法 1.1 Tm计算方法获取Tm主要有常数法(取Tm=281 K)、数值积分法、Bevis公式和近似积分法等4种方法。相比而言,数值积分法最精确,实现也较容易,且数值积分的逼近误差和气象元素误差综合影响也较小[6, 8-10]。我们采用数值积分法计算加权平均温度Tm:
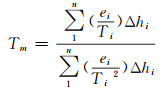
|
(1) |
式中,ei为第i层大气平均水汽压,hPa;Ti为第i层大气平均温度,K;Δhi为第i层大气层厚度,m;ei、ei-1、Ti、Ti-1分别为大气层上界和下界的水汽压和气温:
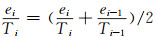
|
(2) |
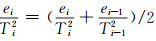
|
(3) |
水汽压不是直接观测量,只能通过露点温度和饱和水汽压公式间接计算。这里选用2008年世界气象组织建议的饱和水汽压计算公式:
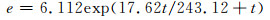
|
(4) |
利用探空资料计算PWV的公式为:

|
(5) |
式中,g为重力加速度,cm/s2;q为比湿,g/kg;P0和PZ为地面与Z高度上的气压,hPa。其中比湿q根据水汽压e来计算:
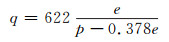
|
(6) |
水汽压e根据下式计算:

|
(7) |
其中,
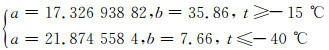
|
(8) |
当气温在-40 ℃~-15 ℃之间时,为冰水共存状态,此时采用两套常数计算出的水汽压相等。所采用的探空资料中包含气象要素露点td和每层气压值p,根据式(5)、(6)、(7)可以计算出PWV。由于资料多、计算量大,需要编制程序计算,式(5)需要离散化为:
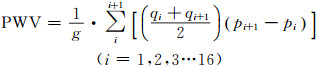
|
(9) |
本文使用非差PPP定位方式计算ZTD[16]。ZTD包括ZWD和ZHD两部分。ZHD由大气中的非水汽成分引起,占总延迟的90%以上,与地面气压有很好的相关性,可以利用相关模型将其修正到mm级; ZWD是由大气中的水汽引起的延迟,占总延迟的10%以下。影响ZWD的因素很复杂,目前用模型估计只能达到10%~20%的精度,模型估计精度很低。所以在GPS定位中,用ZTD减去精确模型计算出的ZHD,即可得到mm级精度的ZWD[17]:
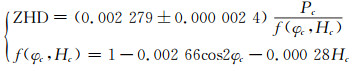
|
(10) |
式中,Pc为测站处气压,hPa;φc为测站地理纬度;Hc为测站海拔高度,km。气压测量精度一般都能达到0.5 hPa,所以式(10)计算的ZHD能达到mm级精度。
PWV定义为单位面积上的垂直空气柱内所有大气中的全部水汽凝结成水后的高度:
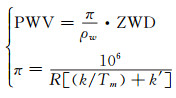
|
(11) |
式中,ρw表示水密度,ZWD的单位是m,π中R=461(J ·kg-1 ·K-1);k=(3.776±0.014)×103 K2 ·hPa-1;K′=16.38 K ·hPa-1;Tm是对流层加权平均温度。可见,Tm的精度对ZWD到PWV的转换精度有直接影响。
2 湖南本地化Tm模型的建立及验证本文选用湖南省长沙、怀化、郴州3个探空站2012~2014年每天8:00和20:00的探空资料数据,采用数值积分法,通过Matlab编程计算Tm和PWV,将基于探空资料计算的Tm和PWV作为参考值,进一步验证本地化Tm模型的精度和可靠性。
2.1 Tm特征分析本文统计了长沙、怀化、郴州3个探空测站利用Bevis公式计算的Tm,比较其差值。限于篇幅,图 1仅列出长沙和怀化站,Bias为两者的偏差。

|
图 1 探空站2012~2014年Tm变化图 Fig. 1 Variation trends of Tm during 2012~2014 at radiosonde stations |
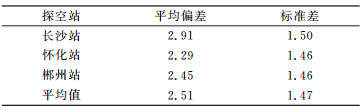
由图 1看出,加权平均温度具有明显的周期性变化,这与季节有直接的关系。不同测站的变化幅度也不相同,这与测站地理位置有明显的关系。从两者的差值可以看出,由Bevis公式计算的Tm与参考值之间存在一定的系统性偏差,这个偏差在不同测站大小不一,说明Bevis公式在不同测站的精度不同。表 1统计了不同探空站的Bevis模型精度,可以看出,Bevis模型在湖南地区存在2.51 K的平均偏差。
|
|
表 1 不同探空站的Bevis-Tm模型精度 Tab. 1 Accuracy of Bevis-Tm at different radiosonde stations |
采用一元线性拟合方法,对长沙、怀化、郴州3个探空站的Ts和Tm作相关性分析。设线性方程为Tm=a+bTs, 可得其误差方程为:
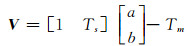
|
(12) |
将从3个探空站数据得到的真值Tm和探空站地面温度Ts代入方程,利用最小二乘原理即可得到系数a、b。则湖南地区的Tm本地化模型为:
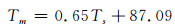
|
(13) |
图 2(a)中的直线表示本地化模型(13),Tm值与Ts值之间的相关系数达到0.942 5。与参考值相比,本地化Tm模型的偏差主要位于-4 K~4 K范围内(图 2(b)),标准差为1.41 K,所以该本地化Tm模型的内符合精度较高,完全符合精度要求(优于3.4 K)[6]。
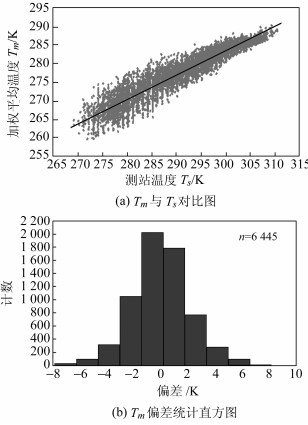
|
图 2 湖南地区Tm建模效果 Fig. 2 Tm modelling results in Hunan region |
利用湖南地区长沙、怀化、郴州3个测站的实测大气探空数据,将利用本地化模型和Bevis公式计算的Tm与参考值(探空数据计算的Tm)进行对比。从表 2和图 3可以看出,本地化Tm模型的精度略高于Bevis模型。就平均偏差而言,本地化模型比Bevis模型小了近1 K,说明本地化模型较好地改正了Bevis模型的系统偏差,更适用于湖南地区。
|
|
表 2 Tm模型精度分析 Tab. 2 Accuracy analysis of Tm model |
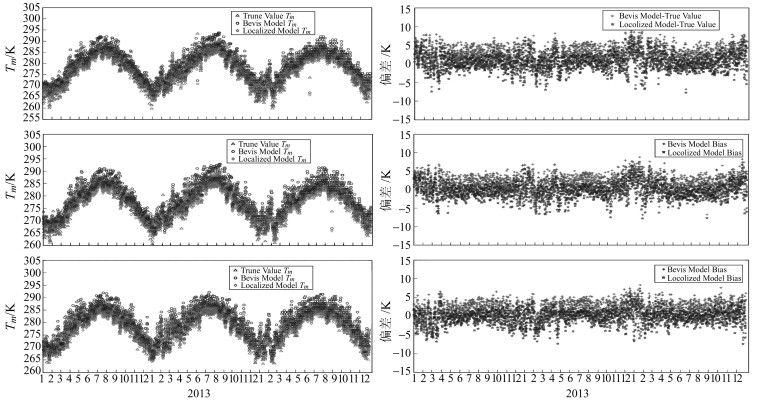
|
图 3 Tm模型偏差分析 Fig. 3 Bias comparison of two Tm models |
湖南省郴州市探空气球站与湖南CORS的CZSQ站共处一地(部分月份数据缺失),我们利用PPP定位方法计算CZSQ于2015年全年的ZTD,分别基于本文的本地化模型和Bevis模型解算得到该站的GPS PWV时间序列[17],并将其与直接利用探空数据得到的PWV进行对比。
图 4(a)为湖南地区本地化Tm模型与探空数据分别计算获得的PWV对比图,图 4(b)为两者的偏差图。可以看出,利用湖南地区本地化模型计算的PWV与利用探空数据直接获得的PWV变化趋势相同,大部分偏差较小。极少部分偏差超过了5 mm,极有可能是探空气球的传感器在突发天气条件下的突然变化所致。结合表 3,平均误差值0.52 mm,标准差为2.21,RMS为2.45,说明本地化模型在获得高精度Tm的基础上,也可以获得高精度的可降水量PWV,比Bevis公式偏差更小、精度更高。
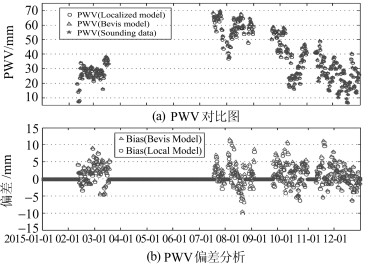
|
图 4 PWV结果比较 Fig. 4 Results comparison of PWV |
|
|
表 3 不同Tm模型的PWV精度比较 Tab. 3 Accuracy comparison between different Tm models |
1) 利用湖南地区长沙、怀化、郴州3个探空站资料,采用数值积分法和最小二乘原理建立了湖南地区的本地化模型Tm=0.65Ts+87.09,相关系数和标准差分别达到0.942 5和1.41 K。
2) 将湖南本地化Tm模型和Bevis模型计算的Tm进行比较可知,湖南地区本地化Tm模型精度优于Bevis模型,平均偏差更小、更符合实际。
3) 基于本地化Tm模型计算的GPS PWV与利用探空数据计算的PWV,平均偏差为0.52 mm,标准差为2.21,RMS为2.45,说明本地化模型不但精度可靠,而且优于Bevis模型。
| [1] |
Bevis M, Businger S, Chiswell S, et al. GPS Meteorology:Mapping Zenith Wet Delays onto Precipitable Water[J]. Journal of Applied Meteorology, 1994, 33(3): 379-386 DOI:10.1175/1520-0450(1994)033<0379:GMMZWD>2.0.CO;2
(  0) 0) |
| [2] |
Duan J, Bevis M, Fang P, et al. GPS Meteorology:Direct Estimation of the Absolute Value of Precipitable Water[J]. Journal of Applied Meteorology, 1996, 35(6): 830-838 DOI:10.1175/1520-0450(1996)035<0830:GMDEOT>2.0.CO;2
(  0) 0) |
| [3] |
姚宜斌, 郭健健, 张豹, 等. 湿延迟与可降水量转换系数的全球经验模型[J]. 武汉大学学报:信息科学版, 2016, 41(1): 45-51 (Yao Yibin, Guo Jianjian, Zhang Bao, et al. A Global Empirical Model of the Conversion Factor between Zenith Wet Delay and Precipitable Water Vapor[J]. Geomatics and Information Science of Wuhan University, 2016, 41(1): 45-51)
(  0) 0) |
| [4] |
Lan Z, Zhang B, Geng Y. Establishment and Analysis of Global Gridded Tm-TsRelationship Model[J]. Geodesy and Geodynamics, 2016, 7(2): 101-107
(  0) 0) |
| [5] |
李建国, 毛节泰, 李成才. 使用全球定位系统遥感水汽分布原理和中国东部地区加权"平均温度"的回归分析[J]. 气象学报, 1999, 57(3): 283-292 (Li Jianguo, Mao Jietai, Li Chengcai. The Approach to Remote Sensing of Water Vapor Based on GPS and Linear Regression Tm in Eastern Region of China[J]. Acta Meteorological Sinica, 1999, 57(3): 283-292 DOI:10.3969/j.issn.1001-7313.1999.03.004)
(  0) 0) |
| [6] |
刘焱雄, 陈永奇, 刘经南. 利用地面气象观测资料确定对流层加权平均温度[J]. 武汉测绘科技大学学报, 2000, 25(5): 400-403 (Liu Yanxiong, Chen Yongqi, Liu Jingnan. Determination of Weighted Mean Tropospheric Temperature Using Ground Meteorological Measurement[J]. Journal of Wuhan Technical University of Surveying and Mapping, 2000, 25(5): 400-403)
(  0) 0) |
| [7] |
谷晓平, 王长耀, 吴登秀. GPS水汽遥感中的大气加权平均温度的变化特征及局地算式研究[J]. 气象科学, 2005, 25(1): 79-83 (Gu Xiaoping, Wang Changyao, Wu Dengxiu. Research on the Local Algorithm for Weighted Atmospheric Temperature Used in GPS Remote Sensing Water Vapor[J]. Scientia Meteorologica Sinica, 2005, 25(1): 79-83 DOI:10.3969/j.issn.1009-0827.2005.01.011)
(  0) 0) |
| [8] |
单九生, 邹海波, 刘熙明, 等. GPS/MET水汽反演中Tm模型的本地化研究[J]. 气象与减灾研究, 2012, 35(1): 42-46 (Shan Jiusheng, Zou Haibo, Liu Ximing, et al. Localization Studies of TmModel in Derivating the GPS/METPrecipitable Water over Jiangxi[J]. Meteorology and Disaster Reduction Research, 2012, 35(1): 42-46 DOI:10.3969/j.issn.1007-9033.2012.01.007)
(  0) 0) |
| [9] |
吕弋培, 殷海涛, 黄丁发, 等. 成都地区大气平均温度建模及其在GPS/PWV计算中的应用研究[J]. 测绘科学, 2008, 33(4): 103-105 (Lü Yipei, Yin Haitao, Huang Dingfa, et al. Modeling of Weighted Mean Atmospheric Temperature and Application in GPS/PWV of Chengdu Region[J]. Science of Surveying and Mapping, 2008, 33(4): 103-105 DOI:10.3771/j.issn.1009-2307.2008.04.035)
(  0) 0) |
| [10] |
王勇, 杨彬云, 刘严萍, 等. 基于无线电探空的武汉大气加权平均温度模型研究[J]. 测绘科学, 2010, 35(2): 112-114 (Wang Yong, Yang Binyun, Liu Yanping, et al. The Study of the Model about Mean Vapor Pressure-Weighted Temperature of the Atmosphere Based on Radiosonde[J]. Science of Surveying and Mapping, 2010, 35(2): 112-114 DOI:10.3969/j.issn.1673-6338.2010.02.010)
(  0) 0) |
| [11] |
朱爽. 北京地区地基GPS加权平均温度计算本地化模型研究[J]. 测绘工程, 2014, 23(4): 28-32 (Zhu Shuang. Research of Local Model of Weighted Mean Temperature of Ground-based GPS in Beijing[J]. Engineering of Surveying and Mapping, 2014, 23(4): 28-32 DOI:10.3969/j.issn.1006-7949.2014.04.007)
(  0) 0) |
| [12] |
张洛恺, 杨力, 王艳玲, 等. 郑州地区大气加权平均温度模型确定[J]. 测绘科学技术学报, 2014, 31(6): 566-569 (Zhang Luokai, Yang Li, Wang Yanling, et al. Modeling of Atmosphere Weighted Mean Temperature of Zhengzhou Region[J]. Journal of Geomatics Science and Technology, 2014, 31(6): 566-569 DOI:10.3969/j.issn.1673-6338.2014.06.004)
(  0) 0) |
| [13] |
陈鹏, 陈家君. 利用NCEP再分析资料建立全球大气加权平均温度模型[J]. 大地测量与地球动力学, 2014, 34(3): 133-136 (Chen Peng, Chen Jiajun. Establishment of Global Atmospheric Weighted Average Temperature Model Using NCEP Reanalysis Data[J]. Journal of Geodesy and Geodynamics, 2014, 34(3): 133-136)
(  0) 0) |
| [14] |
王晓英, 戴仔强, 曹云昌, 等. 中国地区地基GPS加权平均温度Tm统计分析[J]. 武汉大学学报:信息科学版, 2011, 36(4): 412-416 (Wang Xiaoying, Dai Zaiqiang, Cao Yunchang, et al. Weighted Mean Temperature TmStatistical Analysis in Ground-based GPS in China[J]. Geomatics and Information Science of Wuhan University, 2011, 36(4): 412-416)
(  0) 0) |
| [15] |
龚绍琦. 中国区域大气加权平均温度的时空变化及模型[J]. 应用气象学报, 2013, 24(3): 332-334 (Gong Shaoqi. The Spatial and Temporal Variations of Weighted Mean Atmospheric Temperature and Its Models in China[J]. Journal of Applied Meteorological Science, 2013, 24(3): 332-334 DOI:10.3969/j.issn.1001-7313.2013.03.009)
(  0) 0) |
| [16] |
李黎, 匡翠林, 朱建军, 等. 基于实时PPP技术的暴雨短临预报[J]. 地球物理学报, 2012, 55(4): 1129-1136 (Li Li, Kuang Cuilin, Zhu Jianjun, et al. Rainstorm Nowcasting Based on GPSReal-Time Precise Point Positioning Technology[J]. Chinese J Geophys, 2012, 55(4): 1129-1136 DOI:10.6038/j.issn.0001-5733.2012.04.008)
(  0) 0) |
| [17] |
Li Li, Yuan Zhimin, Luo Ping, et al.A System Developed for Monitoring and Analyzing Dynamic Changes of GNSS Precipitable Water Vapor and Its Application[C].China Satellite Navigation Conference (CSNC), 2015 https://rd.springer.com/chapter/10.1007/978-3-662-46638-4_10
(  0) 0) |
2. Hunan Meteorological Bureau, 196 South-Furong Road, Changsha 410118, China;
3. School of Resources Environment and Safety Engineering, Hunan University of Science and Technology, Taoyuan Road, Xiangtan 411201, China
 2017, Vol. 37
2017, Vol. 37