以GM(1, 1)模型为代表的灰色模型在变形监测领域具有广泛应用[1-5]。但灰色模型存在固有缺陷,使其不具备白指数率预测无偏性。其固有缺陷主要表现在背景值构造和初始条件不合理两个方面,也由此导致了各种改进方法[4-10]。背景值构造一直是灰色模型中的研究重点,但是目前的改进方法大多繁复[11]。为此,本文在灰色模型建模基础上,仅增加白化方程与灰微分方程之间参数变换的步骤,使得模型满足无偏性,从而避免繁复。考虑到灰色模型实质上可归结为曲线拟合,本文也采用Origin拟合函数实现灰色模型的建模目标,并对两者在变形监测预报中的应用进行对比。
1 几类无偏灰色模型和Origin拟合函数概述灰色模型以GM(1, 1)模型为基础,后为拓展其应用范围,又提出NGM(1, 1, k)模型[8]、灰色线性回归组合模型和灰色Verhulst模型[12]等。其中,GM(1, 1)模型模拟序列为齐次指数序列,适合于滑坡临滑预测;NGM(1, 1, k)模型和灰色线性回归组合模型的模拟序列都为非齐次指数序列,可用于地基沉降预测;灰色Verhulst模型同样适合于地基沉降预测。
1.1 无偏NGM(1, 1, k)模型NGM(1, 1, k)模型由崔杰等[13]提出,后经证明该模型在参数设置上存在问题,不具备一般性[8, 14]。笔者对其进行改进,并建立了无偏NGM(1, 1, k)模型,不仅解决了参数设置上的问题,而且使得模型满足白指数率预测无偏性[8]。
原始数据序列记为:

|
(1) |
其一次累加值为:
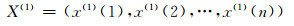
|
(2) |
定义
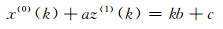
|
(3) |
为无偏NGM (1, 1, k)模型的灰微分方程,即无偏NGM (1, 1, k)模型的定义型。式中,a为发展系数,kb+c为灰作用量,z(1)(k)=0.5(x(1)(k)+x(1)(k-1))。
以最小二乘法确定参数:

|
(4) |
式中,
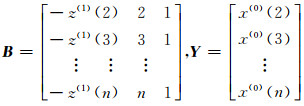
|
(5) |
无偏NGM (1, 1, k)模型的白化方程为:
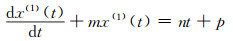
|
(6) |
无偏NGM (1, 1, k)模型的时间响应式为:
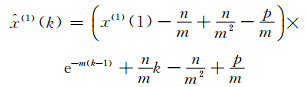
|
(7) |
还原值为:

|
(8) |
白化方程与灰微分方程参数满足以下关系:
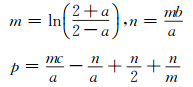
|
(9) |
可以证明,采用上述参数变换公式后,无偏NGM (1, 1, k)模型可满足白指数率预测无偏性,可用于近似非齐次指数序列的分析和预测[8]。
1.2 无偏GM(1, 1)模型参考无偏NGM(1, 1, k)模型建模原理,亦可建立无偏GM(1, 1)模型。定义
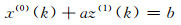
|
(10) |
为无偏GM(1, 1)模型的灰微分方程,即无偏GM(1, 1)模型的定义型。式中,a为发展系数,b为灰作用量,z(1)(k)=0.5(x(1)(k)+x(1)(k-1))。
以最小二乘法确定参数:
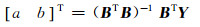
|
(11) |
式中,
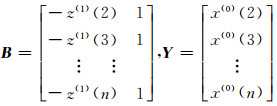
|
(12) |
无偏GM (1, 1)模型的白化方程为:
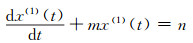
|
(13) |
无偏GM (1, 1)模型的时间响应式为:
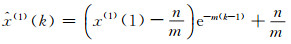
|
(14) |
还原值为:

|
(15) |
参数变换公式推导如下。白化方程(13)的通解为:

|
(16) |
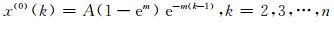
|
(17) |
将式(16)和式(17)代入灰微分方程(10),有:

|
(18) |
为使式(18)成立,有:

|
(19) |
则有:
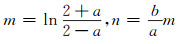
|
(20) |
易证,无偏GM(1, 1)模型满足白指数率预测无偏性,可用于近似齐次指数序列的分析和预测。
1.3 无偏灰色Verhulst模型无偏灰色Verhulst模型的白化方程为:
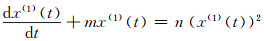
|
(21) |
无偏灰色Verhulst模型的时间响应式为:
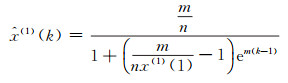
|
(22) |
在应用无偏灰色Verhulst模型时,常遇到原始数据本身呈S型发展的过程。比如地基沉降数据,取原始数据为X(1),建立Verhulst模型直接对X(1)进行模拟[12]。
取y(1)(t)=x(1)(t)-1,代入式(21)可得:

|
(23) |
式中,m1=-m,n1=-n。
显然,式(23)同无偏GM(1, 1)模型的白化方程类似。建立对应的灰微分方程如下:
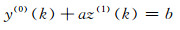
|
(24) |
式中,z(1)(k)=0.5(y(1)(k)+y(1)(k-1))。
以最小二乘法确定参数:

|
(25) |
式中,
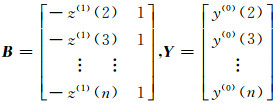
|
(26) |
根据无偏GM (1, 1)模型推导结果,易得:
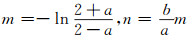
|
(27) |
易证,无偏灰色Verhulst模型满足预测无偏性,可用于近似S型发展序列的分析和预测。
1.4 Origin拟合函数概述上述3种无偏灰色模型通过简单的参数变换,可满足预测无偏性。无偏灰色模型实质上也可归结为曲线拟合问题,即分别采用齐次指数函数、非齐次指数函数和Verhulst函数进行曲线拟合。Origin软件自带多种非线性拟合函数,可实现无偏GM(1, 1)模型、无偏NGM(1, 1, k)模型和无偏灰色Verhulst模型的建模目标,对应3种Exp2PMod1、Exponential、Slogistic3拟合函数:

|
(28) |

|
(29) |
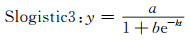
|
(30) |
以黄龙西村滑坡发生前数日的位移监测资料[15]为例,分别建立无偏GM(1, 1)模型、传统GM(1, 1)模型以及Origin拟合函数Exp2PMod1如下:
传统GM(1, 1)模型

|
(31) |
无偏GM(1, 1)模型

|
(32) |
Exp2PMod1

|
(33) |
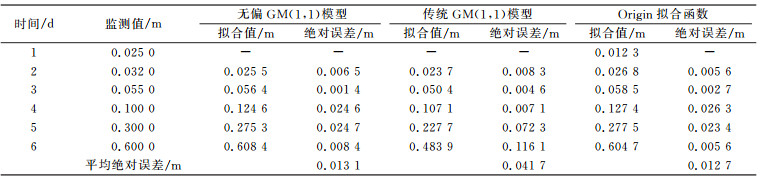
由于GM(1, 1)模型的累加算法,使得还原函数对初始值不存在拟合效果[11],所以只能默认其等于初始值,这是不合理的。为了进行合理对比,在比较拟合精度时,对于传统GM(1, 1)模型和无偏GM(1, 1)模型,不考虑第一组数据,同时Exp2PMod1在应用时也不考虑第一组数据。各种方法拟合结果和拟合精度评价如表 1和图 1所示。可以看出,无偏GM(1, 1)模型的拟合精度明显优于传统GM(1, 1)模型,拟合平均绝对误差由0.041 7 m降到0.013 1 m,说明本文介绍的改进方法是可行的。无偏GM(1, 1)模型和Exp2PMod1的拟合结果和拟合精度非常接近,说明两者拟合效果相当。
|
|
表 1 3种方法拟合结果与监测结果对比 Tab. 1 Comparison of monitoring values and fitting values of the three methods |

|
图 1 3种方法拟合曲线与监测曲线对比 Fig. 1 Comparison of monitoring curve and fitting curves of the three methods |
以向家坡滑坡位移监测资料为例[16],以前1~7周位移监测数据建模,预测8~9周位移,以验证模型精度。分别建立无偏NGM(1, 1, k)模型、无偏GM(1, 1)模型和Origin拟合函数Exponential如下:
无偏NGM(1, 1, k)模型
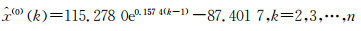
|
(34) |
无偏GM(1, 1)模型(二次累加)
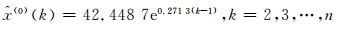
|
(35) |
Exponential

|
(36) |
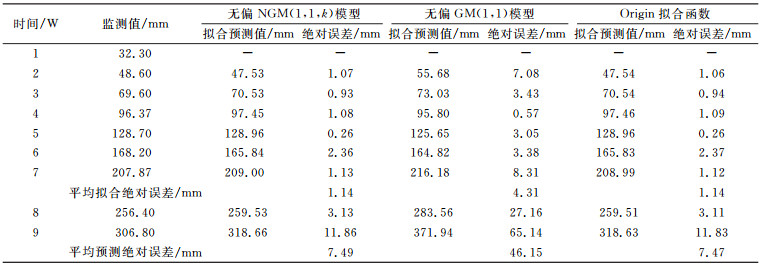
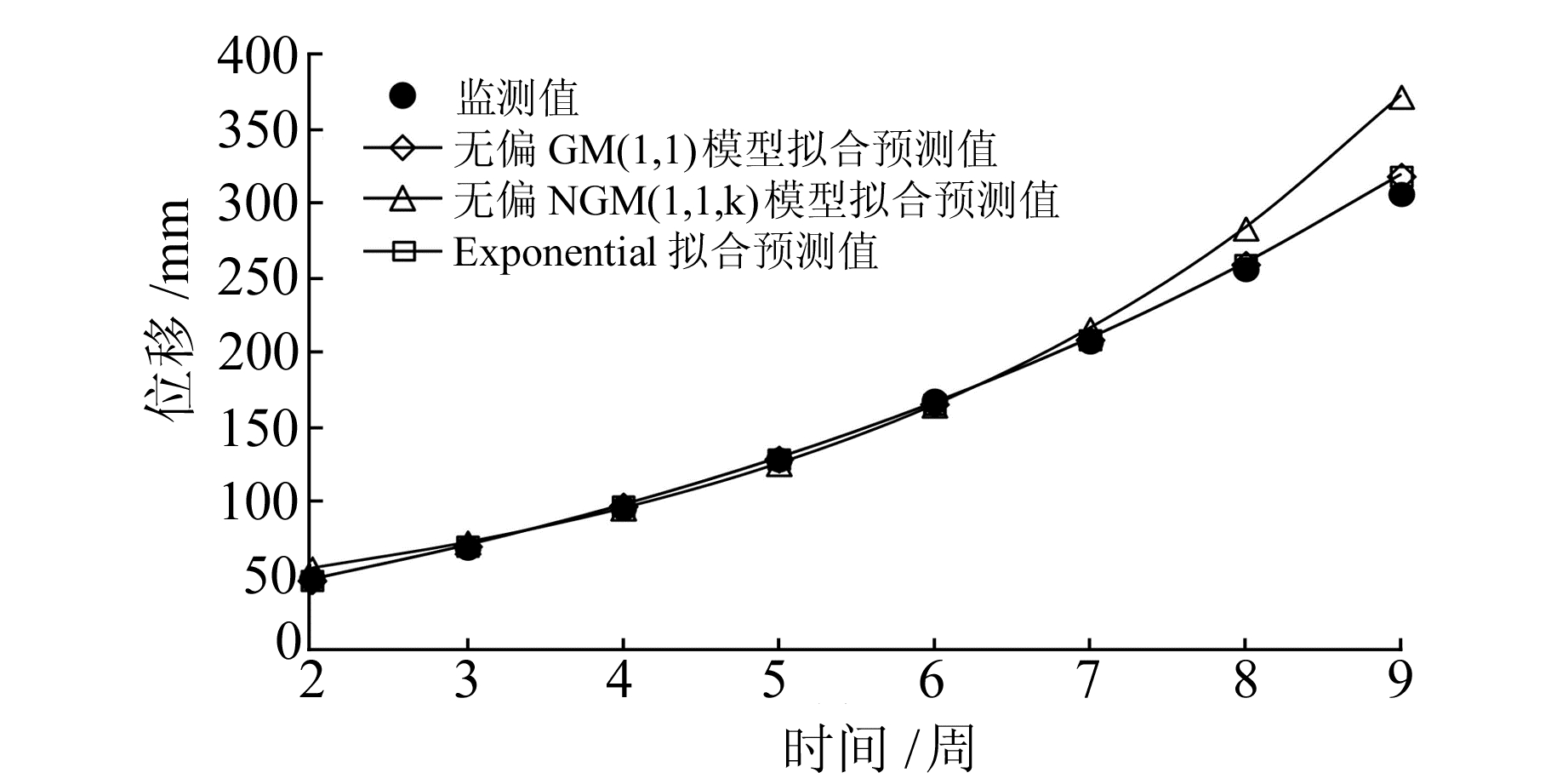
结果如表 2和图 2所示。可以看出,无偏NGM(1, 1, k)模型的拟合和预测精度明显优于无偏GM(1, 1)模型,拟合平均绝对误差由4.31 mm降到1.14 mm,预测平均绝对误差由46.15 mm降到7.49 mm。这说明该滑坡变形趋势更接近于非齐次指数发展趋势。无偏NGM(1, 1, k)模型和Exponential的拟合和预测结果非常接近,拟合和预测精度相当。
|
|
表 2 3种方法拟合结果与监测结果对比 Tab. 2 Comparison of monitoring values and fitting values of the three methods |
|
图 2 3种方法拟合曲线与监测曲线的对比 Fig. 2 Comparison of monitoring curve and fitting curves of the three methods |
以邵阳-怀化高速公路某软土路基断面12期总体沉降实测值为例[17],分别建立无偏灰色Verhulst模型和Origin拟合函数Slogistic3如下:
无偏灰色Verhulst模型

|
(37) |
Slogistic3
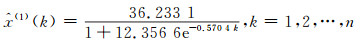
|
(38) |
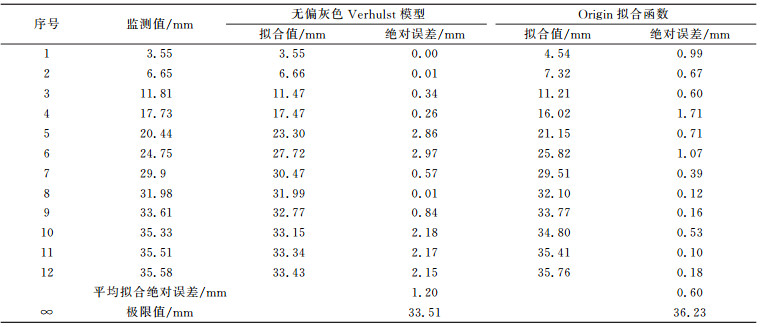
结果如表 3和图 3所示。可以看出,Slogistic3的拟合精度明显优于无偏灰色Verhulst模型,拟合平均绝对误差由1.20 mm降到0.60 mm,且无偏灰色Verhulst模型所预测的沉降极限值为33.51 mm,小于最后一组数据35.58 mm,不符合实际。前2个实例中,无偏灰色模型和Origin拟合函数的拟合预测精度相当,但在本例中出现较大差异。究其原因在于灰色模型仅适合于“小样本”、“贫信息”的不确定问题,其特点是“少数据建模”[12],当数据量较大时,反而不易得到好的拟合精度。
|
|
表 3 2种方法拟合结果与监测结果对比 Tab. 3 Comparison of monitoring values and fitting values of the two methods |

|
图 3 2种方法拟合曲线与监测曲线对比 Fig. 3 Comparison of monitoring curve and fitting curves of the two methods |
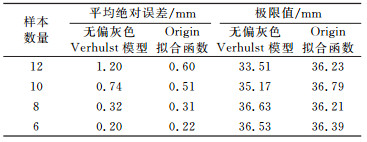
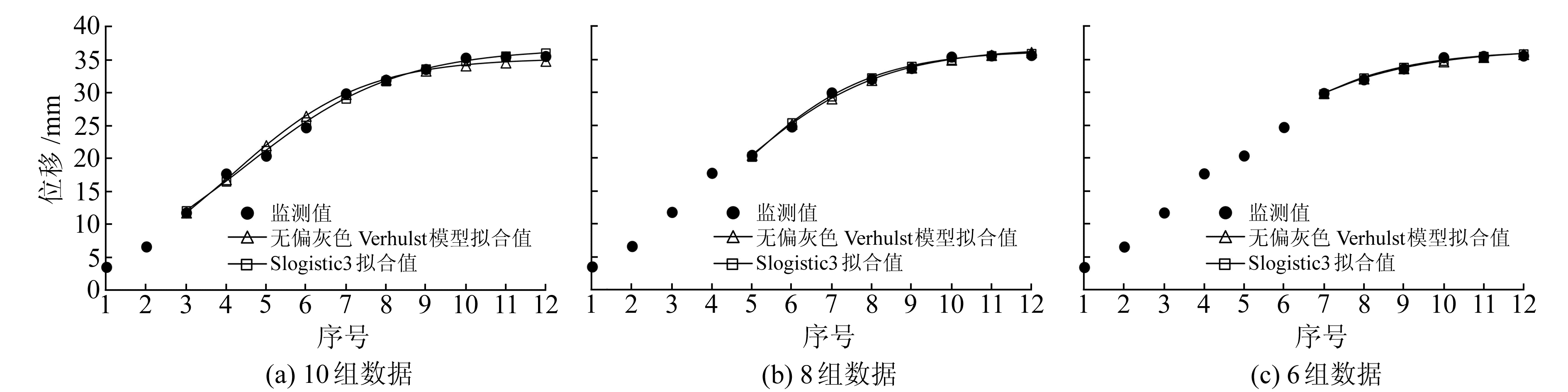
为验证上述观点,不断删除最老的2组数据,再建立无偏灰色Verhulst模型和Slogistic3,所得结果如表 4和图 4所示。可以看出,随着数据量的减少,无偏灰色Verhulst模型与Slogistic3的拟合精度越来越接近。当数据量为8组时,无偏灰色Verhulst模型和Slogistic3的拟合精度达到相当水平,无偏灰色Verhulst模型对沉降极限值的预测结果也更符合实际。
|
|
表 4 不同数据量下两种方法拟合结果与监测结果对比 Tab. 4 Comparison of monitoring values and fitting values of the two methods with different data size |
|
图 4 不同数据量下两种方法拟合曲线与监测曲线对比 Fig. 4 Comparison of monitoring curve and fitting curves of the two methods with different data size |
上述3个实例皆采用等时间间隔变形监测数据,当原始数据存在非等时间间隔情况时,还需增加数据等间隔化的处理步骤。而Origin拟合函数进行曲线拟合时,则不需要考虑这个问题。
3 结语本文所提的无偏灰色模型仅通过白化方程与灰微分方程之间的参数变换实现模型的无偏性,建模原理简单,适合于“小样本”、“贫信息”的不确定问题,在“少数据建模”情况下,其拟合预测精度与Origin拟合函数相当,当建模数据较多时,则不及Origin拟合函数,建议建模数据量不要过多。
| [1] |
文鸿雁, 周吕, 韩亚坤, 等. 基于卡尔曼滤波的GM (1, 1)模型在高铁隧道沉降变形分析中的应用[J]. 大地测量与地球动力学, 2014, 34(1): 88-91 (Wen Hongyan, Zhou Lü, Han Yakun, et al. Study on GM (1, 1) Modeling for Prediction of Deformation under Different Initial Conditions[J]. Journal of Geodesy and Geodynamics, 2014, 34(1): 88-91)
(  0) 0) |
| [2] |
崔伟杰, 包腾飞, 张学峰, 等. 改进的灰色线性回归组合模型在大坝变形监测中的应用[J]. 水电能源科学, 2013, 31(6): 103-105 (Cui Weijie, Bao Tengfei, Zhang Xuefeng, et al. Application of Improved Grey Linear Regression Combination Model in Dam Deformation Monitoring[J]. Water Resources and Power, 2013, 31(6): 103-105)
(  0) 0) |
| [3] |
陈威, 唐德燕, 张届. 利用三点法-灰色组合模型预测铁路路基沉降[J]. 测绘科学, 2015, 40(7): 37-40 (Chen Wei, Tang Deyan, Zhang Jie. Application of Three-Point-Method-Grey GM (1, 1) Combination Model in Settlement Prediction for a Railway Line[J]. Science of Surveying and Mapping, 2015, 40(7): 37-40)
(  0) 0) |
| [4] |
高彩云, 崔希民, 高宁. 顾及不同初始条件的GM (1, 1)变形建模研究[J]. 大地测量与地球动力学, 2014, 34(4): 157-160 (Gao Caiyun, Cui Ximin, Gao Ning. Study on GM (1, 1) Modeling for Prediction of Deformation under Different Initial Conditions[J]. Journal of Geodesy and Geodynamics, 2014, 34(4): 157-160)
(  0) 0) |
| [5] |
李克昭, 李志伟, 孟福军. 基于综合优化GM (1, 1)的形变预测模型[J]. 大地测量与地球动力学, 2016, 36(2): 120-123 (Li Kezhao, Li Zhiwei, Meng Fujun, et al. Deformation Forecasting Model Based on Synthetic and Optimized GM (1, 1)[J]. Journal of Geodesy and Geodynamics, 2016, 36(2): 120-123)
(  0) 0) |
| [6] |
Chen Pengyu, Yu Hongming, Xie Kai. GM (1, 1) Model Based on Optimum Parameters of Whitenization Differential Equation and Its Application on Displacement Forecasting of Foundation Pit[J]. The Journal of Grey System, 2013, 25(1): 54-62
(  0) 0) |
| [7] |
陈鹏宇, 段新胜. 无偏直接PGM (1, 1)模型及其优化[J]. 三峡大学学报:自然科学版, 2009, 31(5): 66-68 (Chen Pengyu, Duan Xinsheng. Unbiased Direct PGM (1, 1) and Its Optimization[J]. Journal of Three Gorges University:Natural Sciences, 2009, 31(5): 66-68)
(  0) 0) |
| [8] |
陈鹏宇, 段新胜, 项翔.优化白化方程参数的新NGM (1, 1, k)模型及其应用[G].第19届灰色系统全国会议, 北京, 2010 (Chen Pengyu, Duan Xinsheng, Xiang Xiang.New GM (1, 1) Model with Optimization Parameters of Whitenization Differential Equation and Its Application[G].The 19th National Conference of Grey System, Beijing, 2010) http://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZGGQ201004001063.htm
(  0) 0) |
| [9] |
陈鹏宇, 段新胜. 基于离散指数函数优化GM (1, 1)模型的重新优化[J]. 三峡大学学报:自然科学版, 2010, 32(1): 88-91 (Chen Pengyu, Duan Xinsheng. Re-optimizing an Optimal GM (1, 1) Model Based on Discrete Function with Exponential Law[J]. Journal of Three Gorges University:Natural Sciences, 2010, 32(1): 88-91)
(  0) 0) |
| [10] |
陈鹏宇, 郎林智. 线性组合背景值构造在GM (1, 1)模型中的优越性分析[J]. 西南师范大学学报:自然科学版, 2010, 35(6): 95-99 (Chen Pengyu, Lang Linzhi. Advantage Analysis of Linear Combination Construction of Background Value in GM (1, 1) Model[J]. Journal of Southwest China Normal University:Natural Science Edition, 2010, 35(6): 95-99)
(  0) 0) |
| [11] |
顾乐民. 对GM灰色模型及理论的分析[J]. 计算机工程与应用, 2016, 52(6): 1-7 (Gu Lemin. Analysis of GM Grey Model and Theory[J]. Computer Engineering and Applications, 2016, 52(6): 1-7 DOI:10.3778/j.issn.1002-8331.1506-0203)
(  0) 0) |
| [12] |
刘思峰, 党耀国, 方志耕, 等. 灰色系统理论及其应用[M]. 北京: 科学出版社, 2010 (Liu Sifeng, Dang Yaoguo, Fang Zhigeng, et al. Grey System Theory and Its Application[M]. Beijing: Science Press, 2010)
(  0) 0) |
| [13] |
崔杰, 党耀国, 刘思峰. 一种新的灰色预测模型及其建模机理[J]. 控制与决策, 2009, 24(11): 1702-1706 (Cui Jie, Dang Yaoguo, Liu Sifeng. Novel Grey Forecasting Model and Its Modeling Mechanism[J]. Control and Decision, 2009, 24(11): 1702-1706 DOI:10.3321/j.issn:1001-0920.2009.11.020)
(  0) 0) |
| [14] |
顾乐民. 对GM灰色模型及理论的质疑[J]. 计算机工程与应用, 2011, 47(30): 58-63 (Gu Lemin. To the GM Grey Model and Theory Question[J]. Computer Engineering and Applications, 2011, 47(30): 58-63 DOI:10.3778/j.issn.1002-8331.2011.30.017)
(  0) 0) |
| [15] |
李秀珍, 孔纪名, 王成华. 灰色GM (1, 1)残差修正模型在滑坡预测中的对比应用[J]. 山地学报, 2007, 25(6): 741-746 (Li Xiuzhen, Kong Jiming, Wang Chenghua. Comparison and Application of Grey GM (1, 1) Modified Residual Error Models in Landslide Predicting[J]. Journal of Mountain Science, 2007, 25(6): 741-746 DOI:10.3969/j.issn.1008-2786.2007.06.015)
(  0) 0) |
| [16] |
王朝阳, 许强, 范宣梅, 等. 灰色新陈代谢GM (1, 1)模型在滑坡变形预测中的应用[J]. 水文地质工程地质, 2009(2): 108-111 (Wang Zhaoyang, Xu Qiang, Fan Xuanmei, et al. Application of Renewal Gray GM (1, 1) Model to Prediction of Landslide Deformation with Two Case Studies[J]. Hydrogeology and Engineering Geology, 2009(2): 108-111 DOI:10.3969/j.issn.1000-3665.2009.02.023)
(  0) 0) |
| [17] |
唐利民, 朱建军. 软土路基沉降泊松模型的正则化牛顿迭代法[J]. 武汉大学学报:信息科学版, 2013, 38(1): 69-73 (Tang Limin, Zhu Jianjun. Regularized Newton Iterative Algorithm for Poisson Model of Soft Clay Embankment Settlement[J]. Geomatics and Information Science of Wuhan University, 2013, 38(1): 69-73)
(  0) 0) |
 2017, Vol. 37
2017, Vol. 37