2. 长安大学地质工程与测绘学院,西安市雁塔路126号,710054;
3. 西部矿产资源与地质工程教育部重点实验室,西安市雁塔路126号,710054;
4. 地理信息工程国家重点实验室,西安市雁塔路中段1号,710054;
5. 中铁隧道勘察设计院有限公司,天津市河北大街1号,300133
原子钟是导航信号形成和系统测距的星上时间基准,其性能直接决定用户的导航定位精度。北斗二代在轨卫星搭载国产铷钟,其精度和稳定性相对差于GPS和Galileo,因此开展北斗系统星载钟的数据质量控制方法研究对提高北斗导航系统定位性能具有重要价值[1-2]。目前已有的钟差研究成果主要集中在卫星钟差的建模和预报方面,涉及数据质量控制的研究较少,且大部分成果均是针对GPS钟差序列的研究[3-8]。钟差序列的数据质量控制是后续卫星钟性能研究的前提,其对于卫星钟差的建模与预报至关重要。由于我国的北斗二代卫星系统属于起始运行阶段,卫星钟差序列并不十分稳定,出现钟跳、粗差和数据中断的频率较高,需要对其数据质量进行严格控制,从而保障其钟差性能和精度[9-10]。
本文结合北斗钟差序列的特点和规律,提出一种综合考虑钟跳、粗差和数据中断异常的数据质量控制方法,并从粗差剔除效果、周期项探测以及钟差序列拟合预报3个方面分析论证所提方法的有效性。
1 卫星钟差数据质量控制方法 1.1 常规质量控制方法目前对GPS系统的星载钟差序列研究较多,其常用的数据质量控制内容主要包括相频数据的转换、数据绘图分析、数据跳变、间断的处理以及粗差的处理。相关文献给出了处理不合格钟差序列的具体方法[11-13],但大都是针对特殊典型情况进行的单一方法研究。对于GPS卫星钟差序列,同时出现多个异常现象的几率较小,因此单一方法对其适用。但由于北斗星载钟差序列中同时出现钟跳、粗差、中断等异常的频率较高,仅依照适用于GPS卫星钟差序列处理的单一质量控制方法不能有效控制北斗卫星钟差序列的质量,因此本文提出北斗二代卫星钟差的数据质量控制方案。
1.2 北斗二代钟差的数据质量控制方法北斗卫星钟差的数据质量控制主要包括3个方面:钟跳的识别、异常数据和粗差的剔除、缺失数据的插补。
1) 钟跳的识别。钟跳在原子钟时域稳定性测量中是不可避免的,相位跳变对应于频率峰值。根据这一特点,本文通过设定合适的阈值(根据实验结果得出,北斗取1×10-5 s作为阈值较合适)对频率数据进行判断并确定钟跳位置。若单天钟差序列内部出现钟跳,需要分段处理。
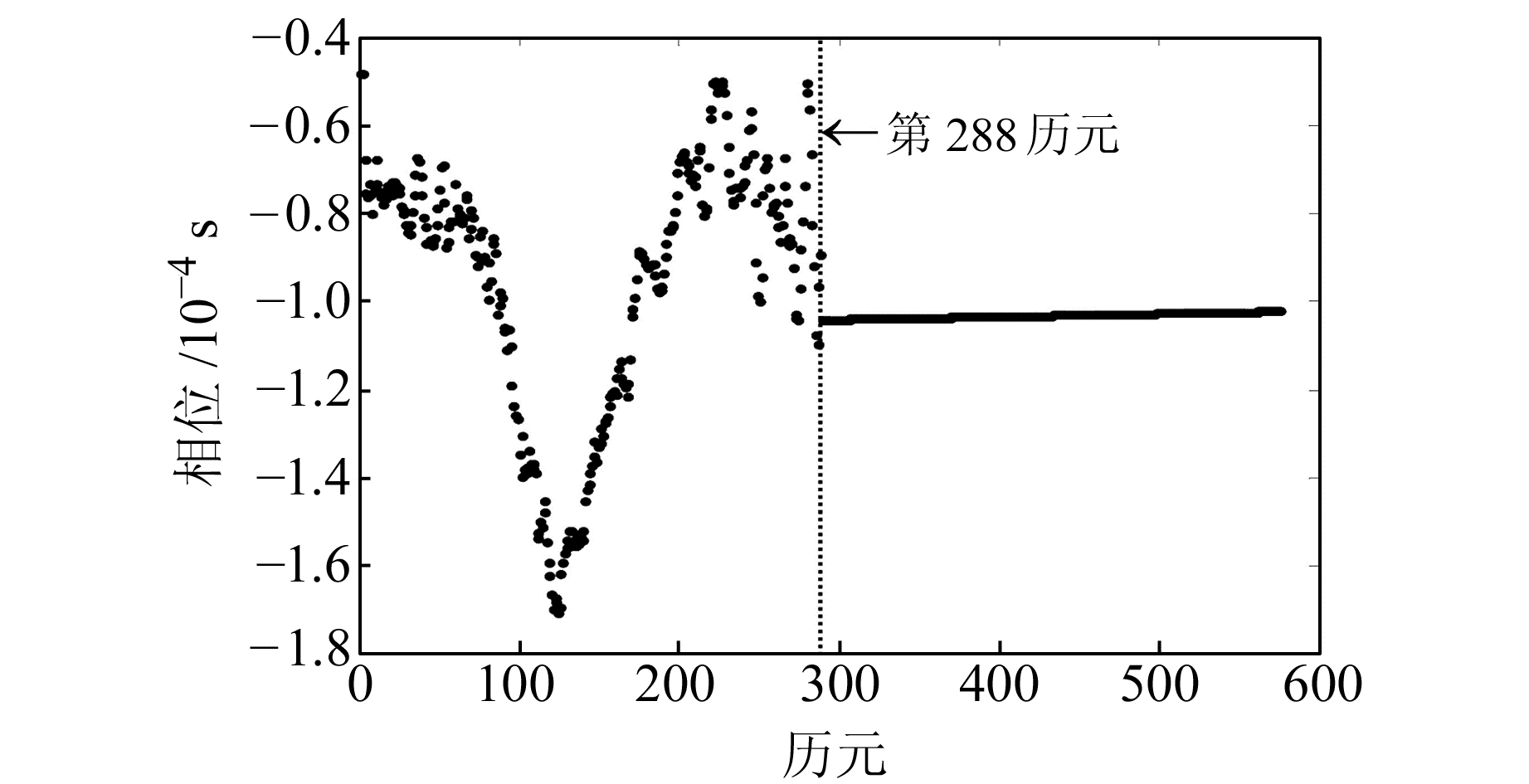
2) 异常数据段和粗差的剔除。①异常数据段的剔除。对北斗二代各颗卫星的长期钟差序列进行绘图分析发现,各卫星钟差序列可能同时出现数据异常,且持续时间以d为单位。通过判断其频率峰值的量级及峰值出现的频次,识别异常数据段,并按天对其进行剔除处理。图 1为C01卫星2013年046和047 d的原始钟差序列,图中第1~288历元的数据段即为异常数据段。②粗差的剔除。采取综合MAD和Baarda方法共同探测粗差。MAD方法为钟差序列常用方法,故本文仅介绍Baarda探测法。
|
图 1 C01卫星钟差序列的异常数据段 Fig. 1 The abnormal segment of C01 satellite clock bias series |
Baarda数据探测法[14]可以有效地探测粗差并将其剔除。钟差模型有一次多项式模型和二次多项式模型。但是在粗差探测过程中,钟漂对钟差的影响远远小于粗差的量级,因此选择一次多项式模型构建钟差观测方程,这样既可以减小计算量,又不影响粗差探测的实际结果。钟差一次模型为:

|
(1) |
式中,ti为观测时刻,Xi为ti的观测钟差,t0为起始时刻,X0为起始时刻钟差,B为相对钟速,εi为随机误差,i=1, 2, …, n。其中,t0可根据情况而定,X0、B为待求参数。
根据最小二乘法可求得X0、B。为了计算方便,取起始时刻t0为n次观测时刻值ti的平均值。钟差观测值的残差为:
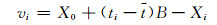
|
(2) |
钟差检验统计量为标准化残差:
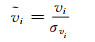
|
(3) |
式中,σvi是vi的标准差。
对于构建的检验统计量ṽi,给定限差值k(一般取k=3),若|ṽi|>k,则可判定Xi存在粗差。
3) 缺失数据的插补。北斗卫星原始钟差序列中存在的缺失数据分为2种情况,一种是缺失一整天数据,全部用零值替代;另一种是单天内缺失少量数据,采取线性插值作内插处理[15],对于需要外插的数据进行置零处理,防止因外插时段过长而得到不可靠的钟差序列。
2 算法流程首先,获取各颗北斗卫星的长期钟差序列,将缺失历元的钟差数据设置为极大值999 999.999 999,使其与标准钟差文件匹配。其次,依次处理单天钟差序列,合并为长期卫星钟差序列。
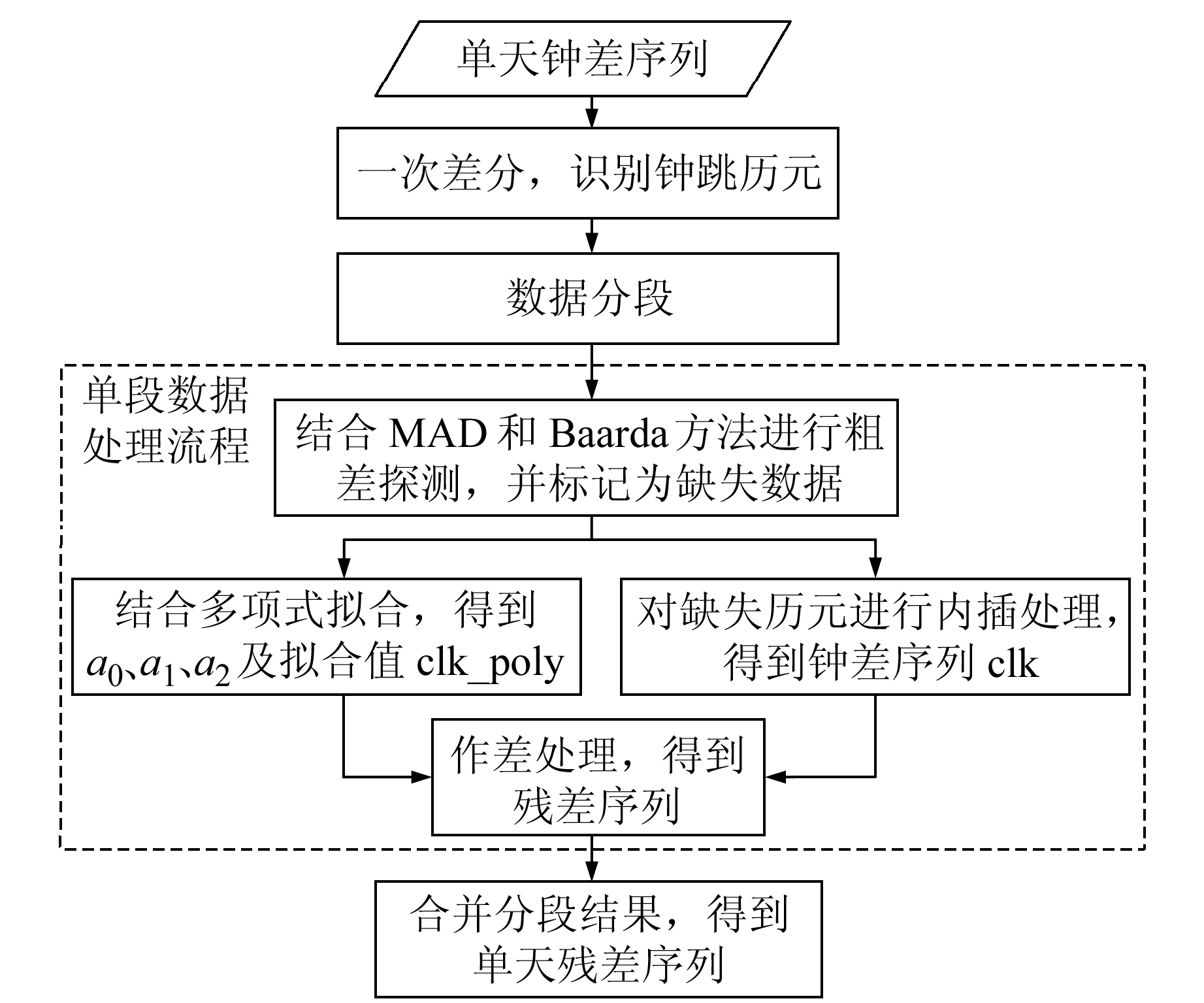
图 2为对单天钟差序列进行数据质量控制的流程。其中,通过一次差分识别钟跳历元时,采用实验得到的经验阈值1×10-5 s作为判断依据。图 2中的a0、a1、a2分别对应相位、频率、频漂3个参数。对缺失数据进行线性内插处理后得到钟差序列clk,即为经过数据质量控制后得到的钟差序列。通过合并单天序列获取长期序列,利用阈值法进行粗差剔除(以残差序列标准差的2倍作为阈值),最终获取较为干净的残差序列。
|
图 2 北斗卫星钟差数据质量控制基本流程 Fig. 2 The basic flow of data quality control method for Beidou satellite clock bias |
选取2013-02-12~12-31共323 d的北斗卫星精密钟差数据(由武汉大学GNSS中心提供),采样间隔为5 min,从多天原始钟差文件中分别提取单颗卫星的长期钟差序列进行数据质量控制处理。
为了验证本文提出的数据质量控制方法的有效性,按照不同星座选取卫星号分别为C01(GEO)、C06(IGSO)、C11(MEO)的3颗卫星进行实验。实验内容包括钟差序列的粗差剔除、周期项探测以及拟合预报。
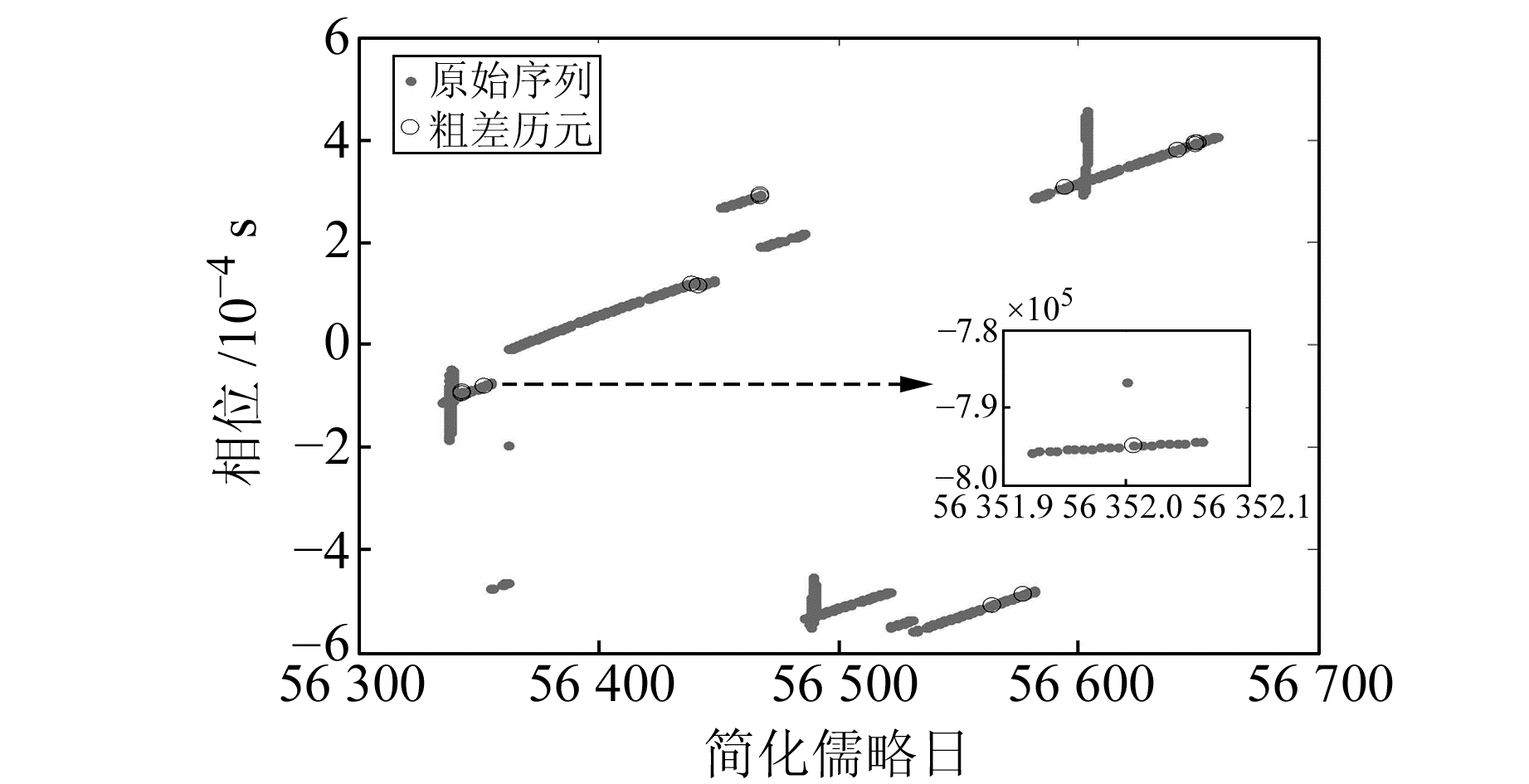
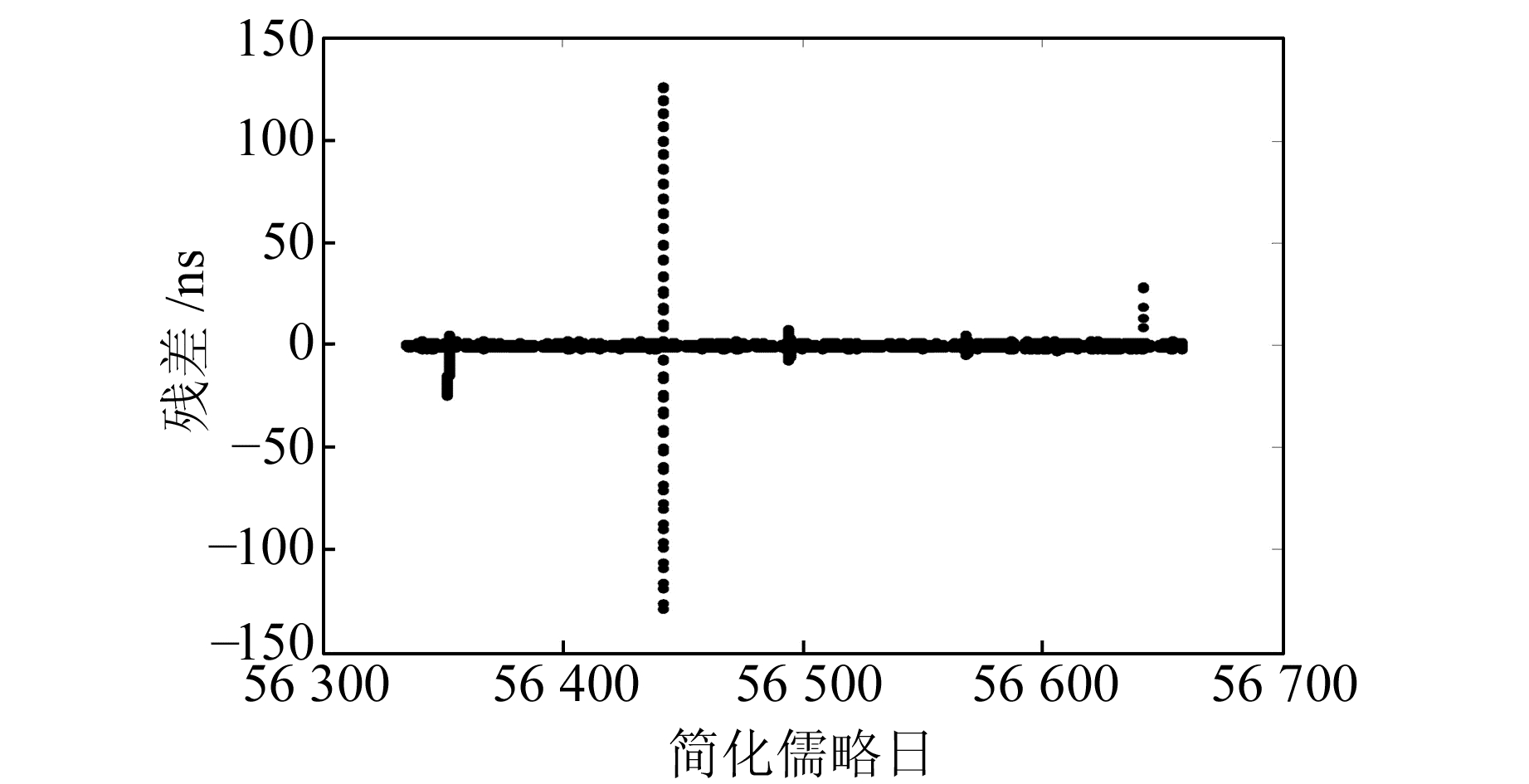
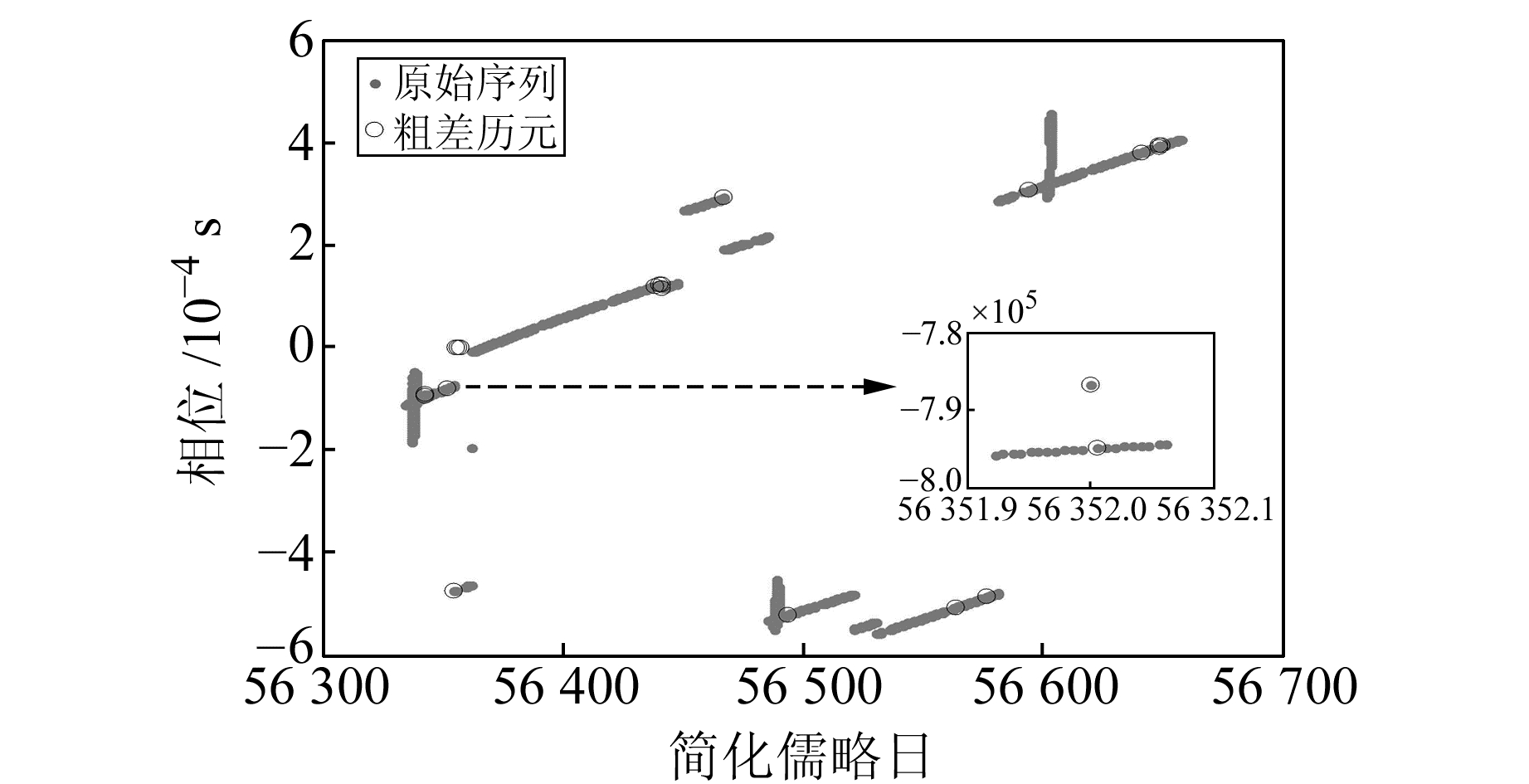
3.1 钟差序列的粗差剔除结果分析为了验证数据质量控制方法中Baarda粗差探测法的有效性,采用基于MAD的数据质量控制方法(方法一)以及本文提出的数据质量控制方法(方法二)处理长期钟差序列,得到扣除二次趋势项的残差序列,对其进行对比分析。限于篇幅,这里仅列出C01卫星的结果。图 3、图 4和图 5、图 6分别为采用方法一和方法二获取的粗差结果和预处理后的残差序列。
|
图 3 C01卫星钟差序列的粗差探测结果(方法一) Fig. 3 The gross error detection result of C01 satellite clock error series with method Ⅰ |
|
图 4 C01卫星数据预处理后的残差序列(方法一) Fig. 4 The residual sequence of C01 satellite pretreatment data with method Ⅰ |
|
图 5 C01卫星钟差序列的粗差探测结果(方法二) Fig. 5 The gross error detection result of C01 satellite clock error series with method Ⅱ |
|
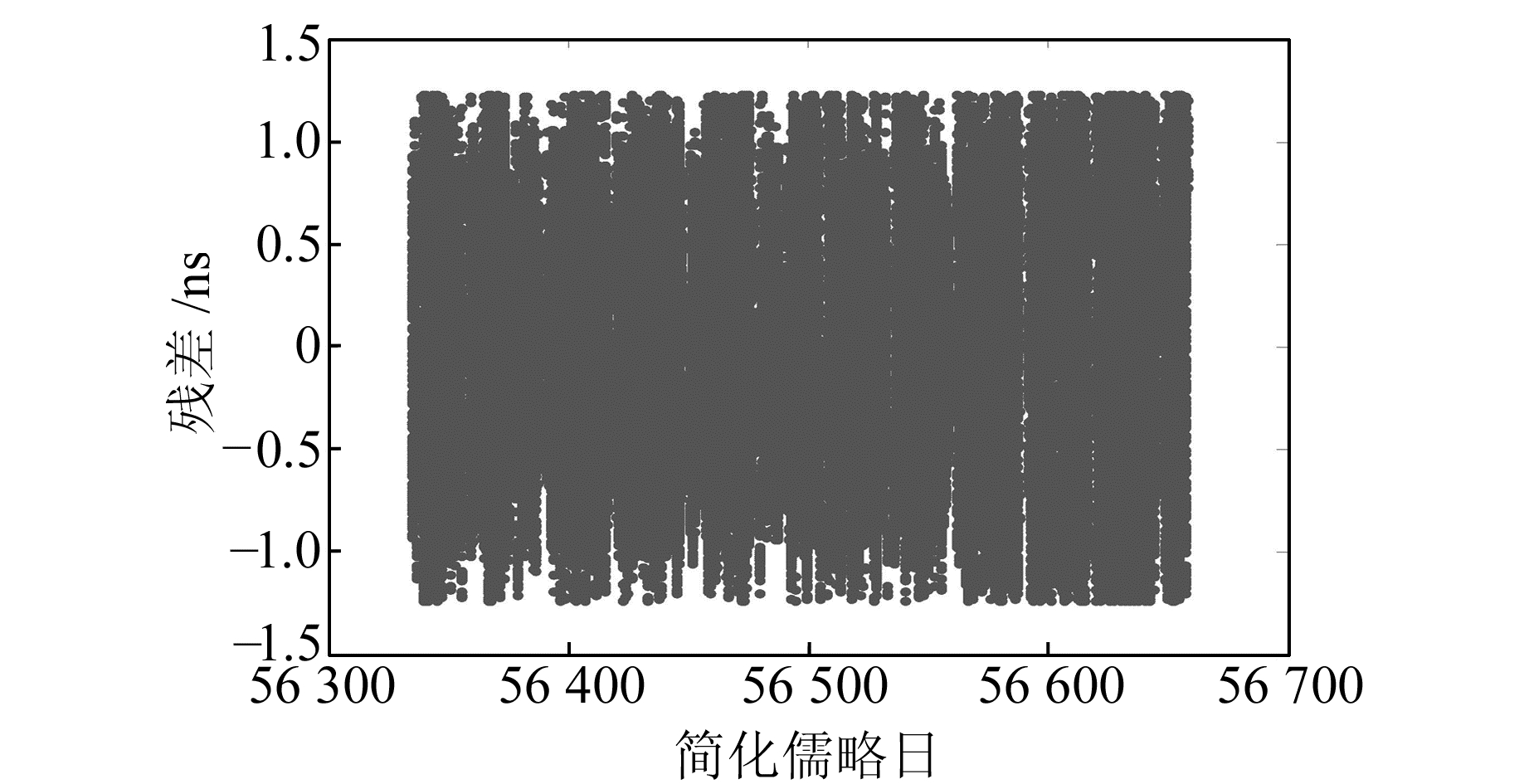
图 6 C01卫星数据预处理后的残差序列(方法二) Fig. 6 The residual sequence of C01 satellite pretreatment data with method Ⅱ |
对比图 3和图 5可以看出,MAD法在进行粗差探测时会遗漏某些粗差历元,而Baarda探测法弥补了它的不足,因此综合采用MAD和Baarda共同探测粗差可以更全面地剔除粗差。
对比图 4和图 6看出,两种方法得到的残差序列量级差异较大,进一步验证了方法二的有效性。采用方法二处理原始钟差序列可以获取更为干净的残差序列。
3.2 周期项分析利用频谱分析对扣除趋势项的卫星钟差残差序列进行分析,研究卫星钟的周期性[16]。采用快速傅里叶变换方法(FFT)将残差序列从时域转换到频域,得到频谱图。频谱图中较大的谱峰幅值对应的频率值即为时域信号包含的主要频率项,从而可以转化为主要周期[17]。
对原始钟差序列仅扣除二次项趋势,得到残差序列r1。采用本文质量控制方法处理钟差序列,得到残差序列r2。分别对2组残差序列进行频谱分析(图 7~图 12)。
|
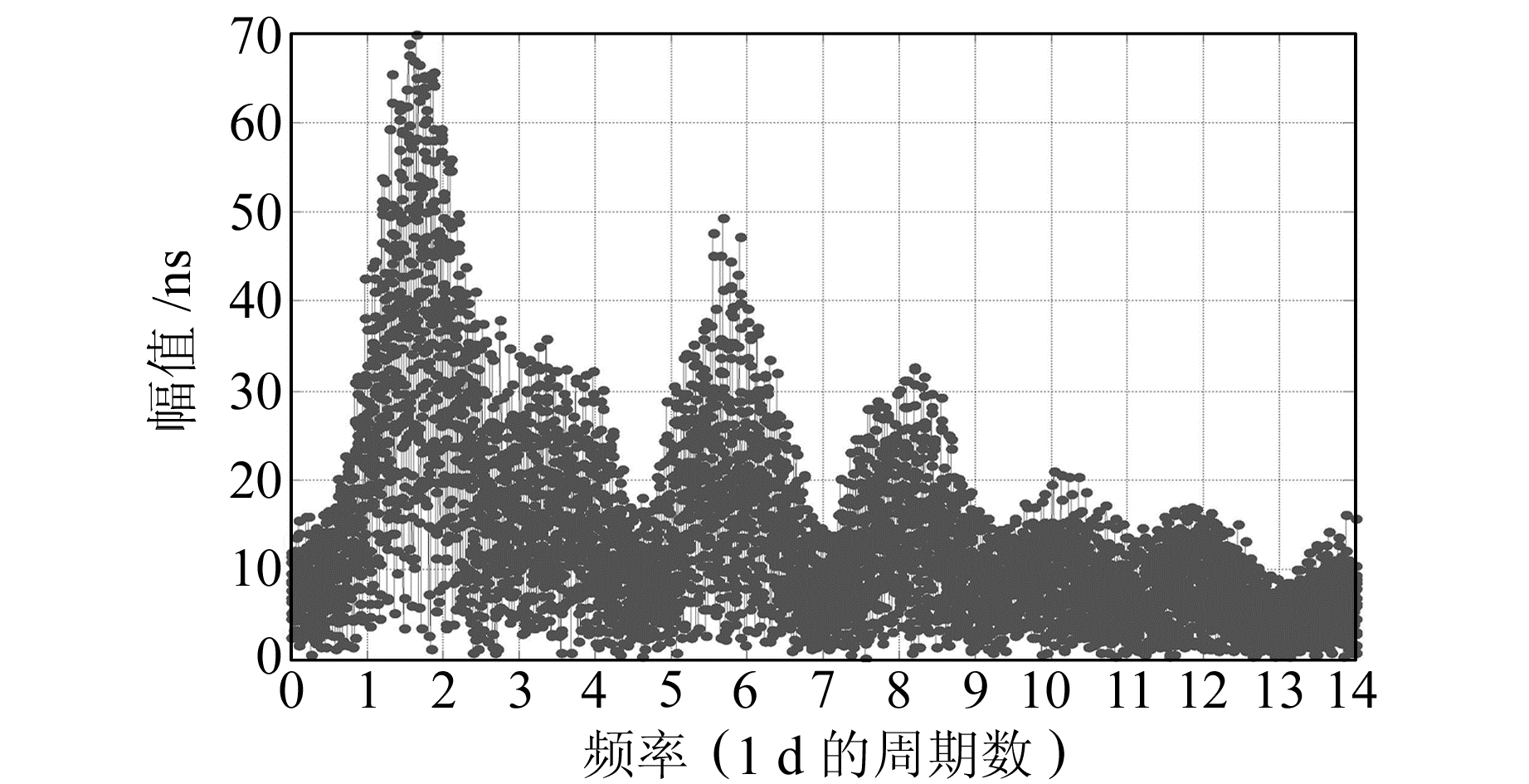
图 7 C01卫星r1残差序列频谱分析图 Fig. 7 The spectrum analysis result of C01 satellite's r1 residual series |
|
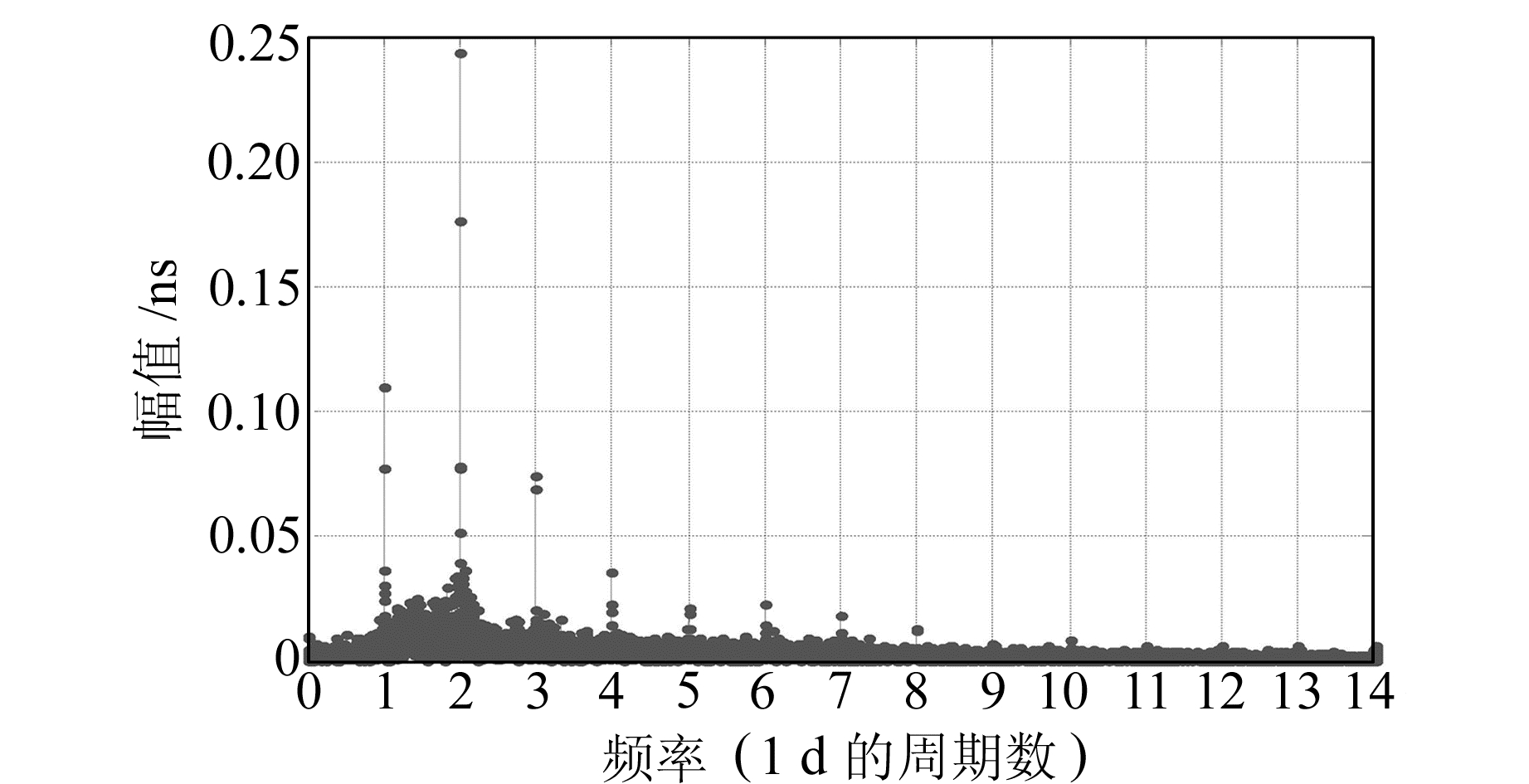
图 8 C01卫星r2残差序列频谱分析图 Fig. 8 The spectrum analysis result of C01 satellite's r2 residual series |

|
图 9 C06卫星r1残差序列频谱分析图 Fig. 9 The spectrum analysis result of C06 satellite's r1 residual series |
|
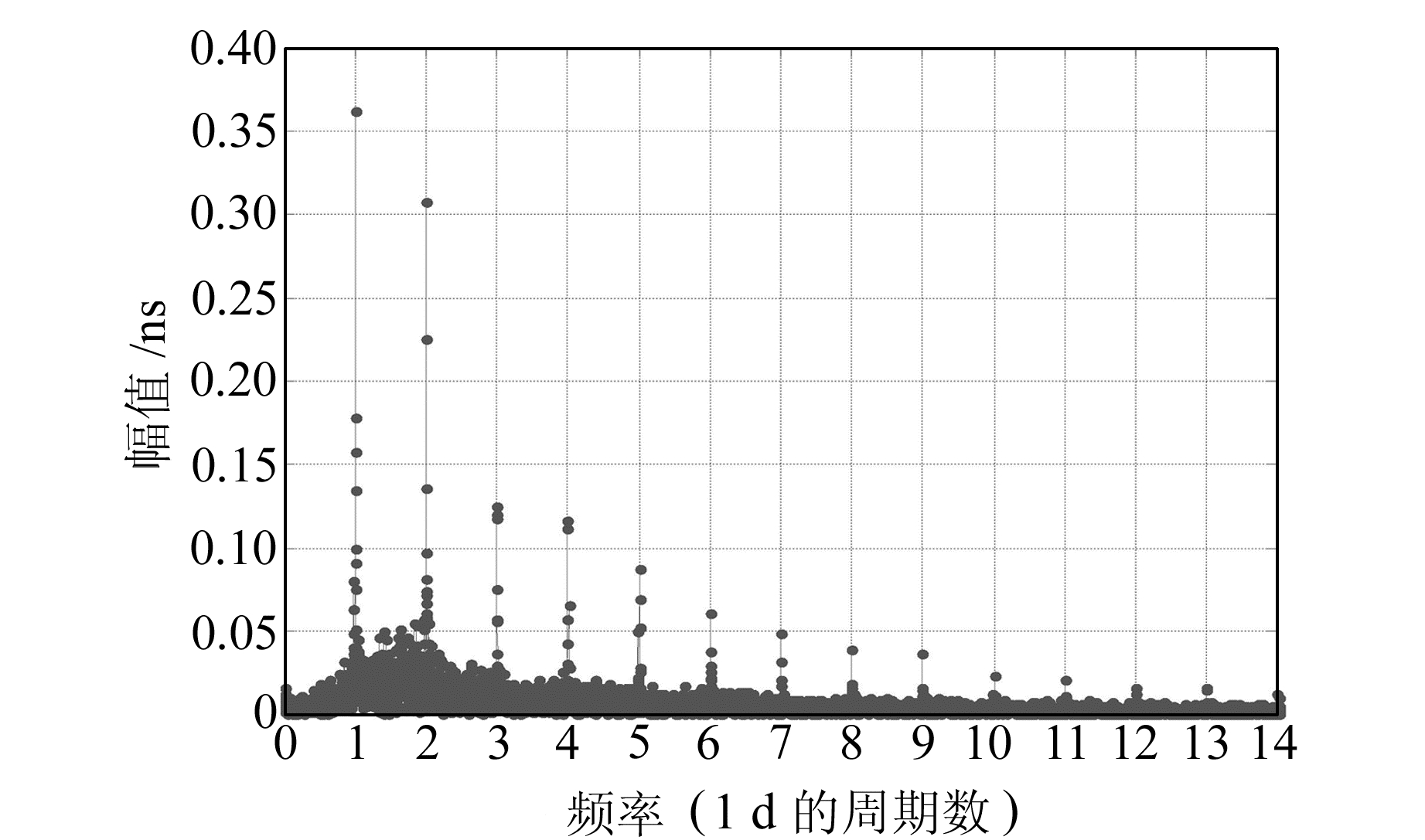
图 10 C06卫星r2残差序列频谱分析图 Fig. 10 The spectrum analysis result of C06 satellite's r2 residual series |
|
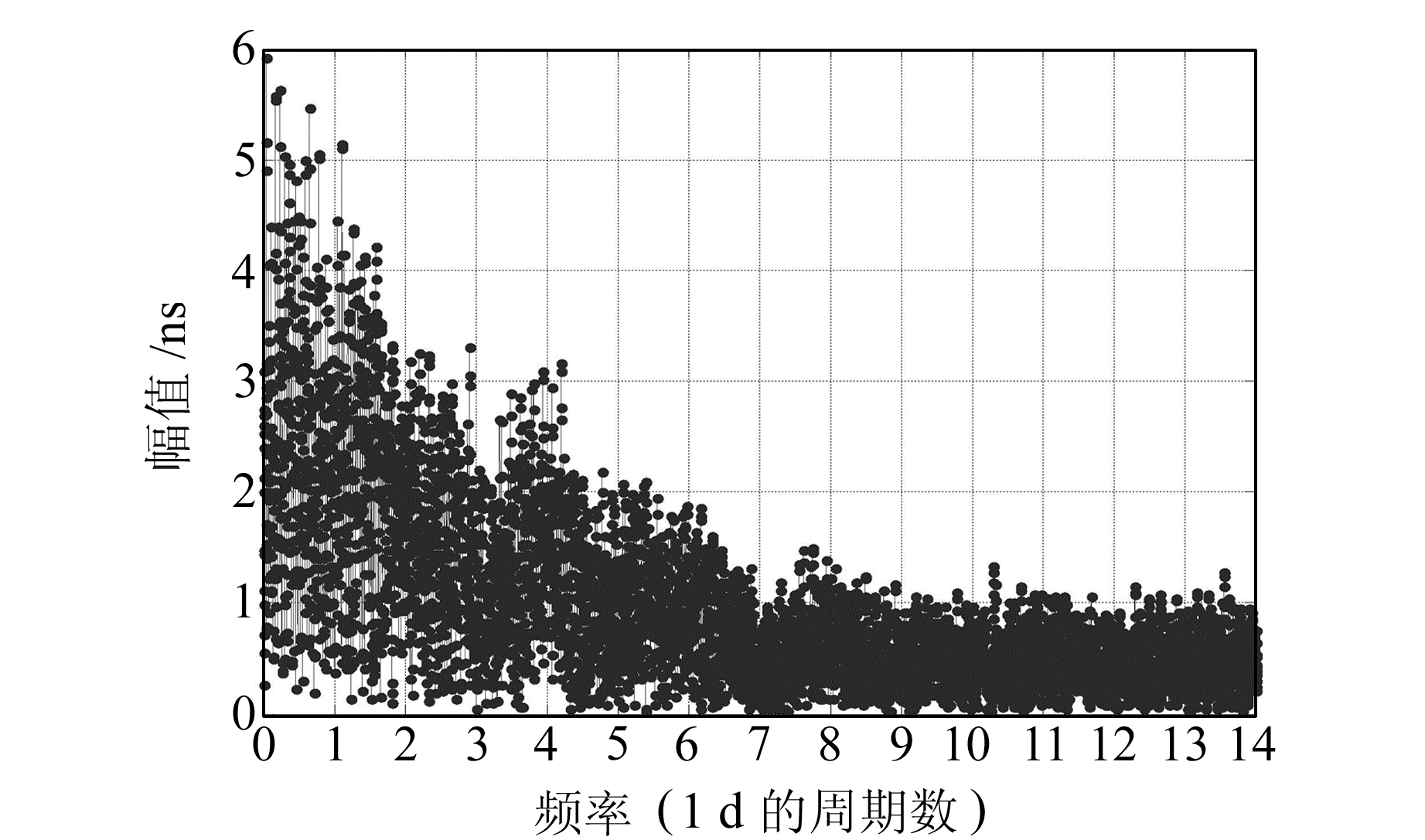
图 11 C11卫星r1残差序列频谱分析图 Fig. 11 The spectrum analysis result of C11 satellite's r1 residual series |
|
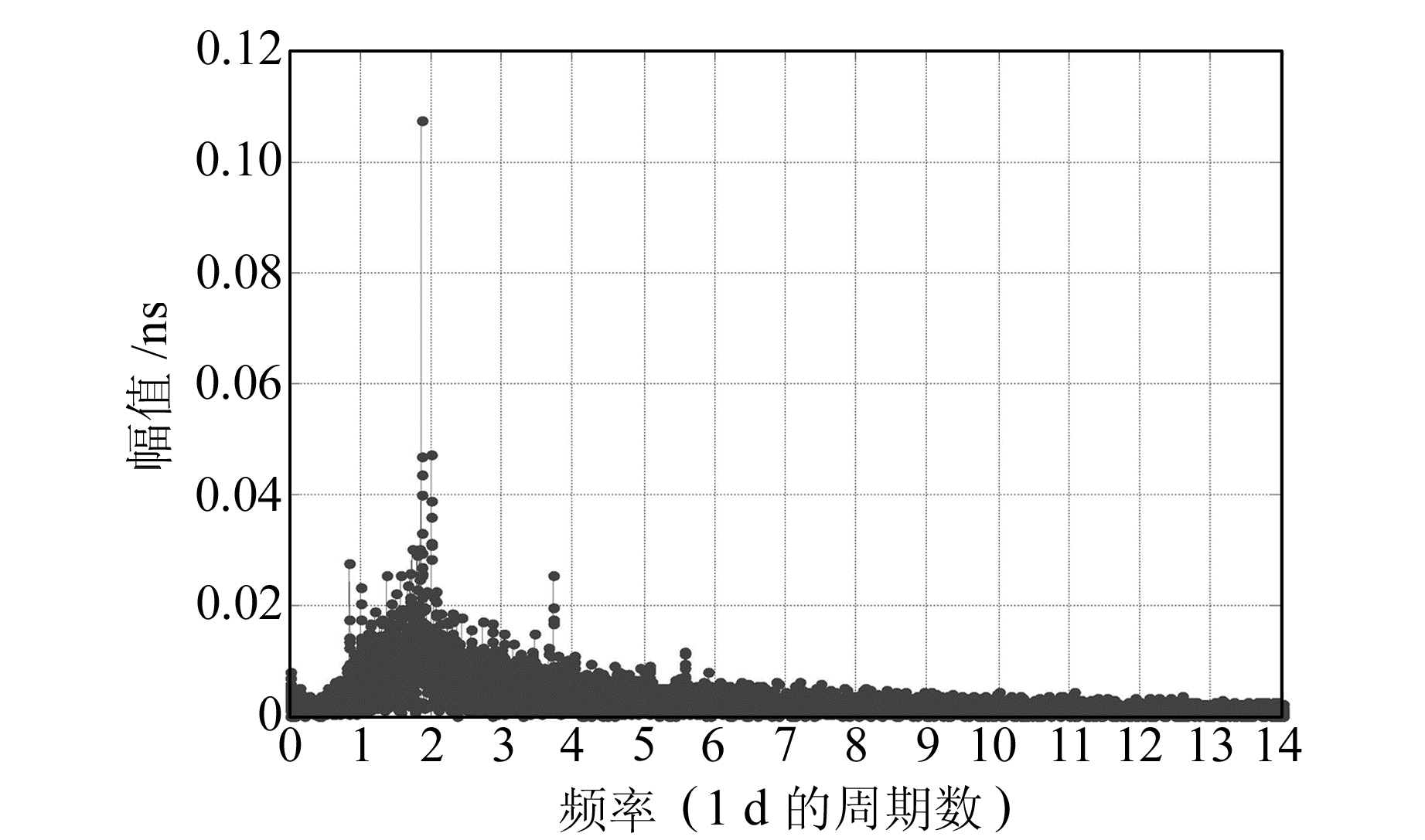
图 12 C11卫星r2残差序列频谱分析图 Fig. 12 The spectrum analysis result of C11 satellite's r2 residual series |
图 7、图 9、图 11难以分辨谱峰,因此无法确定其显著周期项。通过对图 8、图 10、图 12的频谱图分析,可以提取出各颗卫星的显著周期项。按照谱峰值大小降序排列,各颗卫星钟差序列对应的主要周期项如下:C01卫星为12 h、24 h、8 h、6 h;C06卫星为24 h、12 h、8 h、6 h;C11卫星为12 h、24 h、6 h。
对比3颗卫星的r1和r2残差序列频谱分析结果可以看出,对r2残差进行频谱分析能得到更加清晰可靠的谱峰,从而确定其主要频率和周期。
对北斗现有的14颗卫星进行钟差数据质量控制处理,分析其频谱结果,3类卫星均可得到相似的周期项结论。
3.3 钟差的拟合预报为进一步验证本文提出的数据质量控制方法在钟差拟合预报中的有效性,分别采用原始钟差序列和经过数据质量控制处理的钟差序列进行建模预报。利用单天钟差数据建立二次多项式模型,预报次日钟差。
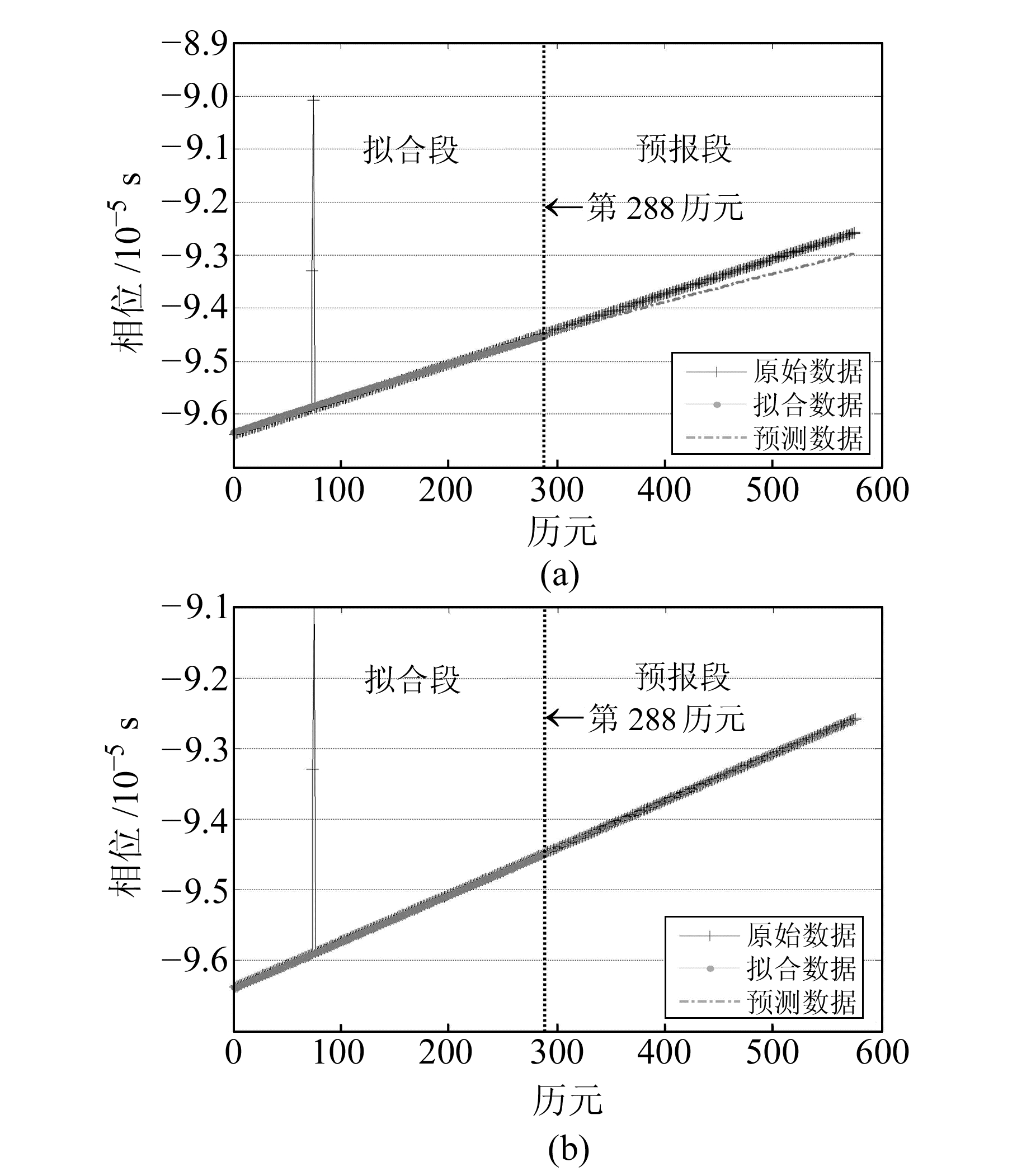
选取C01卫星2013年第051 d钟差序列建模,预报第052 d钟差序列,结果见图 13。选取C01卫星2013年第175 d数据作为建模数据,预报第176 d钟差序列,结果见图 14。图 13和图 14中,图(a)和(b)的差别为建模数据是否进行过质量控制处理。
|
图 13 C01卫星第051 d拟合预报结果 Fig. 13 The fitting and forecast results of C01 satellite data from the 51th day of the year |

|
图 14 C01卫星第175 d拟合预报结果 Fig. 14 The fitting and forecast results of C01 satellite data from the 175th day of the year |
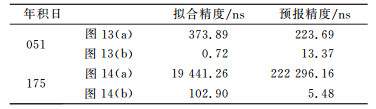
图 14(a)表明,由于建模数据段发生钟跳,导致二次项拟合结果完全偏离原序列趋势,因此预报结果是不可靠的。图 14(b)表明,本文提出的方法可以有效识别钟跳并进行分段拟合,利用离预报时刻最近的一段钟差数据建模并预报,避免钟跳对预报的不利影响。图 14(b)中数值为0的时间段是由于钟跳前后数据中断,对该段数据作了置零处理。由表 1中第175 d的结果可以看出,钟跳对预报建模的精度影响很大。
|
|
表 1 C01卫星钟差拟合预报精度结果 Tab. 1 The fitting and forecast accuracy results of C01 satellite clock bias |
结合图 13、图 14及表 1,可以证明本文提出的数据质量控制方法的有效性及必要性。
4 结语本文针对北斗二代卫星钟差序列的特点,提出了一种卫星钟差的数据质量控制方法,并分别从粗差剔除效果、周期项探测以及钟差序列拟合预报3个方面验证了该方法的有效性及必要性。通过对钟差序列进行质量控制,可以获取钟差序列中更可靠更真实的信息(如周期性),并且在数据存在异常情况下大大提高了预报精度。
由于精密钟差数据常应用于实时精密单点定位中,实时钟差质量控制将会对确保可靠高精度的定位具有更重要的作用,因此实时数据质量控制算法将是下一步研究的重点。
致谢: 感谢武汉大学提供的北斗钟差数据。
| [1] |
黄观文.GNSS星载原子钟质量评价及精密钟差算法研究[D].西安: 长安大学, 2012 (Huang Guanwen. Research on Algorithms of Precise Clock and Quality Evaluation of GNSS Satellite Clock[D]. Xi'an: Changan University, 2012) http://cdmd.cnki.com.cn/Article/CDMD-10710-1013017231.htm
(  0) 0) |
| [2] |
Steigenberger P, Hugentobler U, Hauschild A, et al. Orbit and Clock Analysis of Compass GEO and IGSO Satellites[J]. Journal of Geodesy, 2013, 87(6): 515-525 DOI:10.1007/s00190-013-0625-4
(  0) 0) |
| [3] |
朱祥维, 肖华, 雍少为, 等. 卫星钟差预报的Kalman算法及其性能分析[J]. 宇航学报, 2008, 29(3): 966-970 (Zhu Xiangwei, Xiao Hua, Yong Shaowei, et al. The Kalman Algorithm Used for Satallite Clock Offset Prediction and Its Performance Analysis[J]. Journal of Astronautics, 2008, 29(3): 966-970 DOI:10.3873/j.issn.1000-1328.2008.03.045)
(  0) 0) |
| [4] |
王继刚, 胡永辉, 何在民, 等. 组合模型预报导航卫星钟差[J]. 大地测量与地球动力学, 2012, 32(1): 84-88 (Wang Jigang, Hu Yonghui, He Zaimin, et al. Combination Models for Navigation Satellite Clock Prediction[J]. Journal of Geodesy and Geodynamics, 2012, 32(1): 84-88)
(  0) 0) |
| [5] |
戴伟, 焦文海, 李维鹏, 等. GPS Block IIR(M)星载原子钟钟差预报研究[J]. 大地测量与地球动力学, 2009, 29(4): 111-115 (Dai Wei, Jiao Wenhai, Li Weipeng, et al. Research on Clock Error Prediction for Atomic Clocks Loaded on GPS Block IIR(M) Satellite Clocks[J]. Journal of Geodesy and Geodynamics, 2009, 29(4): 111-115)
(  0) 0) |
| [6] |
黄观文, 杨元喜, 张勤. 开窗分类因子抗差自适应序贯平差用于卫星钟差参数估计与预报[J]. 测绘学报, 2011, 40(1): 15-21 (Huang Guanwen, Yang Yuanxi, Zhang Qin. Estimate and Predict Satellite Clock Error Using Adaptively Robust Sequential Adjustment with Classified Adaptive Factors Based on Opening Windows[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(1): 15-21)
(  0) 0) |
| [7] |
Lei Y, Hu Z P, Zhao D N. A Novel Method for Navigation Satellite Clock Bias Prediction Considering Stochastic Variation Behavior[C]. China Satellite Navigation Conference, Nanjing, 2014
(  0) 0) |
| [8] |
Huang G W, Zhang Q, Xu G C. Real-Time Clock Offset Prediction with an Improved Model[J]. GPS Solution, 2014, 18(1): 95-104 DOI:10.1007/s10291-013-0313-0
(  0) 0) |
| [9] |
陈建鹏, 毛悦, 贾小林, 等.原子钟稳定性在轨评估计算影响分析[C].中国卫星导航学术年会, 北京, 2010 (Chen Jianpeng, Mao Yue, Jia Xiaolin, et al. Analysis of On-Board Atomic Clock Stability Influences[C]. China Satellite Navigation Conference, Beijing, 2010)
(  0) 0) |
| [10] |
郭海荣, 杨元喜. 导航卫星原子钟时域频率稳定性影响因素分析[J]. 武汉大学学报:信息科学版, 2009, 34(2): 218-221 (Guo Hairong, Yang Yuanxi. Analyses of Main Error Sources on Time Domain Frequency Stability for Atomic Clocks of Navigation Satellites[J]. Geomatics and Information Science of Wuhan University, 2009, 34(2): 218-221)
(  0) 0) |
| [11] |
郭海荣.导航卫星原子钟时频特性分析理论与方法研究[D].郑州: 信息工程大学, 2006 (Guo Hairong. Research on Theory and Method of Domain Frequency Stability for Atomic Clocks of Navigation Satellites[D]. Zhengzhou: Information Engineering University, 2006)
(  0) 0) |
| [12] |
杨元喜. 北斗区域卫星导航系统基本导航定位性能初步评估[J]. 中国科学:地球科学, 2014, 44(1): 72-81 (Yang Yuanxi. Preliminary Assessment of the Navigation and Positioning Performance of Beidou Regional Navigation Satellity System[J]. Science China:Earth Science, 2014, 44(1): 72-81)
(  0) 0) |
| [13] |
Riley W J. Handbook of Frequency Stablity Analysis[Z]. NIST Special Publication 1065, 2008
(  0) 0) |
| [14] |
李跃华, 蔺玉亭, 张达, 等.钟差数据处理方法研究[C].中国卫星导航学术年会, 上海, 2011 (Li Yuehua, Lin Yuting, Zhang Da, et al. Method Research on Clock Deviation Process[C]. China Satellite Navigation Conference, Shanghai, 2011)
(  0) 0) |
| [15] |
洪樱, 欧吉坤, 彭碧波. GPS卫星精密星历和钟差三种内插方法的比较[J]. 武汉大学学报:信息科学版, 2006, 31(6): 517-518 (Hong Ying, Ou Jikun, Peng Bibo. Three Interpolation Methods for Precise Ephemeris and Clock Offset of GPS Satellite[J]. Geomatics and Information Science of Wuhan University, 2006, 31(6): 517-518)
(  0) 0) |
| [16] |
黄观文, 张勤, 许国昌, 等. 基于频谱分析的IGS精密星历卫星钟差精度分析研究[J]. 武汉大学学报:信息科学版, 2008, 33(5): 496-499 (Huang Guanwen, Zhang Qin, Xu Guochang, et al. IGS Precise Satellite Clock Model Fitting and Its Precision by Using Spectral Analysis Method[J]. Geomatics and Information Science of Wuhan University, 2008, 33(5): 496-499)
(  0) 0) |
| [17] |
Senior K L, Ray J R, Beard R L. Characterization of Periodic Variations in the GPS Satellite Clocks[J]. GPS Solution, 2008, 12(3): 211-225 DOI:10.1007/s10291-008-0089-9
(  0) 0) |
2. College of Geology Engineering and Geomatic, Chang'an University, 126 Yanta Road, Xi'an 710054, China;
3. Key Laboratory of Western China's Mineral Resources and Geological Engineering, Ministry of Education 126 Yanta Road, Xi'an 710054, China;
4. State Key Laboratory of Geographic Information Engineering, 1 Mid-Yanta Road, Xi'an 710054, China;
5. China Railway Tunnal Survey and Design Institute Co Ltd, 1 Hebei Street, Tianjin 300133, China
 2017, Vol. 37
2017, Vol. 37