GNSS信号在穿过电离层时,其传播速度会因受到电离层折射的影响而改变,从而在GNSS定位中引起一个误差,即电离层延迟误差。由于电离层是一种色散介质,这个误差大小与其信号频率及传播路径上的总电子含量(TEC)有关[1]。对于GNSS单频用户,电离层误差通常是利用全球或者区域性电离层延迟模型进行改正,而这些模型的确立是建立在对电离层TEC变化规律长期研究的基础上的。此外,监测电离层TEC在空间天气预报和地震前兆信息获取方面有着重要的作用[2-4]。
由于电离层延迟与GNSS信号的频率有关,使用双频观测值可以获取电离层TEC。学者们在这方面开展了大量研究工作[5-10]。例如,蔡昌盛等[5]使用伪距和载波相位组合观测值进行了电离层TEC计算;聂文锋等[6]利用GPS双频观测数据进行区域电离层TEC的提取,并对提取得到的TEC精度进行了对比分析;王晓岚等[7]综合研究了利用双频GPS观测值反演电离层总电子含量和硬件延迟偏差的方法。这些研究工作大都只使用了GPS的双频观测数据。随着三频信号的出现,Spits等[8]利用伽利略GIOVE-A/-B导航卫星的三频观测数据进行TEC的计算分析,指出与使用双频观测数据计算相比,使用三频观测数据能得到更高精度的TEC值。
最近几年随着GNSS的快速发展,BDS和Galileo卫星均能发送三频信号,GPS卫星中已有多颗卫星发射三频信号,三频数据为电离层TEC的计算提供了更多的观测数据。在三频观测数据中使用不同的频率组合,可以得到不同的电离层TEC值,如何充分利用各频率数据获取精确的TEC是值得研究的问题。本文在分析硬件延迟偏差对不同频率观测值计算TEC影响的基础上,提出了一种使用三频观测数据计算绝对TEC的方法。
1 利用三频数据确定电离层TEC的方法 1.1 传统双频数据计算电离层TEC的方法在只顾及一阶电离层延迟误差的情况下,电离层TEC可以通过测码伪距观测值获取,其计算公式如下[9]:

|
(1) |
式中,f1、f2分别为载波L1和L2上的频率;P1、P2分别为f1、f2频率上的测码伪距观测值;B12为频间硬件延迟偏差;TEC12P表示使用f1和f2频率上的伪距观测数据计算得出的TEC值,其单位为TECu,1TECu=1016个电子/m2。由于多路径效应可以通过合适选址、天线加装抑径板和扼流圈等措施削减,因此式(1)中未考虑多路径误差。
由于伪距观测值精度较差,可以使用载波相位观测值对伪距进行平滑处理[5]:
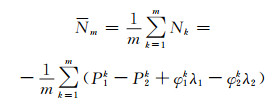
|
(2) |
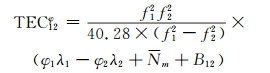
|
(3) |
式中,m为观测历元数,Nm为载波相位线性组合后的模糊度项,φ1、φ2分别为f1、f2频率上的载波相位观测值,λ1、λ2为对应频率波长,上标k表示第k个历元。从式(1)和式(3)可以看出,要想获得绝对的电离层TEC值,需要对硬件延迟偏差进行改正。另外,利用载波相位观测值对伪距进行平滑之前,需要保证载波相位观测值未发生周跳或者已经对周跳进行了修复。
1.2 频间硬件延迟偏差类似式(1),利用f1、f3频率上的伪距观测值也可以获得电离层TEC。对于同一颗GNSS卫星不同频率的信号,它们穿过电离层的路径是相同的,理论上通过不同频率组合获得的TEC值应该是一样的。但由于存在不同的频间硬件延迟偏差,不同频率数据计算获得的TEC值将存在显著差异。对f1、f2组合和f1、f3组合的TEC计算式求差,可得系统硬件延迟偏差与伪距观测值之间的关系:

|
(4) |
式中,
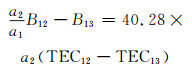
|
(5) |
将“ 
根据式(3),可获得加入硬件延迟偏差改正后的TEC曲线。但由于观测噪声以及硬件延迟偏差改正数据本身的精度限制,通过不同频率两两组合获得的TEC曲线之间仍存在细微差异。为了获得唯一的TEC曲线值,笔者进行了如下推导。
硬件延迟偏差包含卫星硬件延迟偏差BS和接收机硬件延迟偏差BR。在短时间内,硬件延迟偏差值可视为稳定值。IGS在提供硬件延迟偏差产品的同时也提供了对应产品的精度(STD)。值得注意的是,IGS提供的硬件延迟偏差的单位为ns,因此在进行误差传播时需要注意换算为m。通过误差传播定律,可获得系统硬件延迟偏差方差:
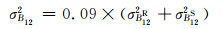
|
(6) |
经过载波相位观测值平滑后的观测值具有很好的平滑性,其精度主要受模糊度计算精度的影响。从式(2)可以看出,模糊度项Nm的精度主要由伪距观测值组合(P1k-P2k)和平滑历元数m决定。以载波平滑伪距观测值Φ=φ1kλ1-φ2kλ2+Nm为参考值,(P1k-P2k)的方差可按式(7)进行计算:

|
(7) |
由于载波相位观测值精度较高,忽略其噪声影响,可以获得Nm的方差为σP122/m。则在利用式(3)计算TEC时,其TEC的方差由误差传播率可得:
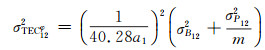
|
(8) |
利用式(8),同理可得f1、f3频率观测值计算TEC的方差σ2TECφ13,从而可以利用式(9)进行加权平均计算:

|
(9) |
式中,TEC123φ为合成的最终绝对TEC值;TEC12φ和TEC13φ分别为经相位平滑伪距后f1、f2频率和f1、f3频率观测值计算得到的绝对TEC值。式(9)即为利用三频观测数据计算合成绝对TEC的公式。
2 实验结果与分析 2.1 实验数据采用IGS网站2015-04-11的GNSS多系统多频观测数据进行实验计算,为方便不同系统之间的对比,选取了3个测站具有较多GPS、BDS和GALILEO三频卫星数据的观测时段。具体测站信息及采用的卫星和观测值类型见表 1和表 2,3个测站分别来自于高纬度、中纬度和低纬度地区。
|
|
表 1 测站相关信息 Tab. 1 Station information |
|
|
表 2 各系统观测卫星及观测值类型 Tab. 2 The type of satellite and observation |
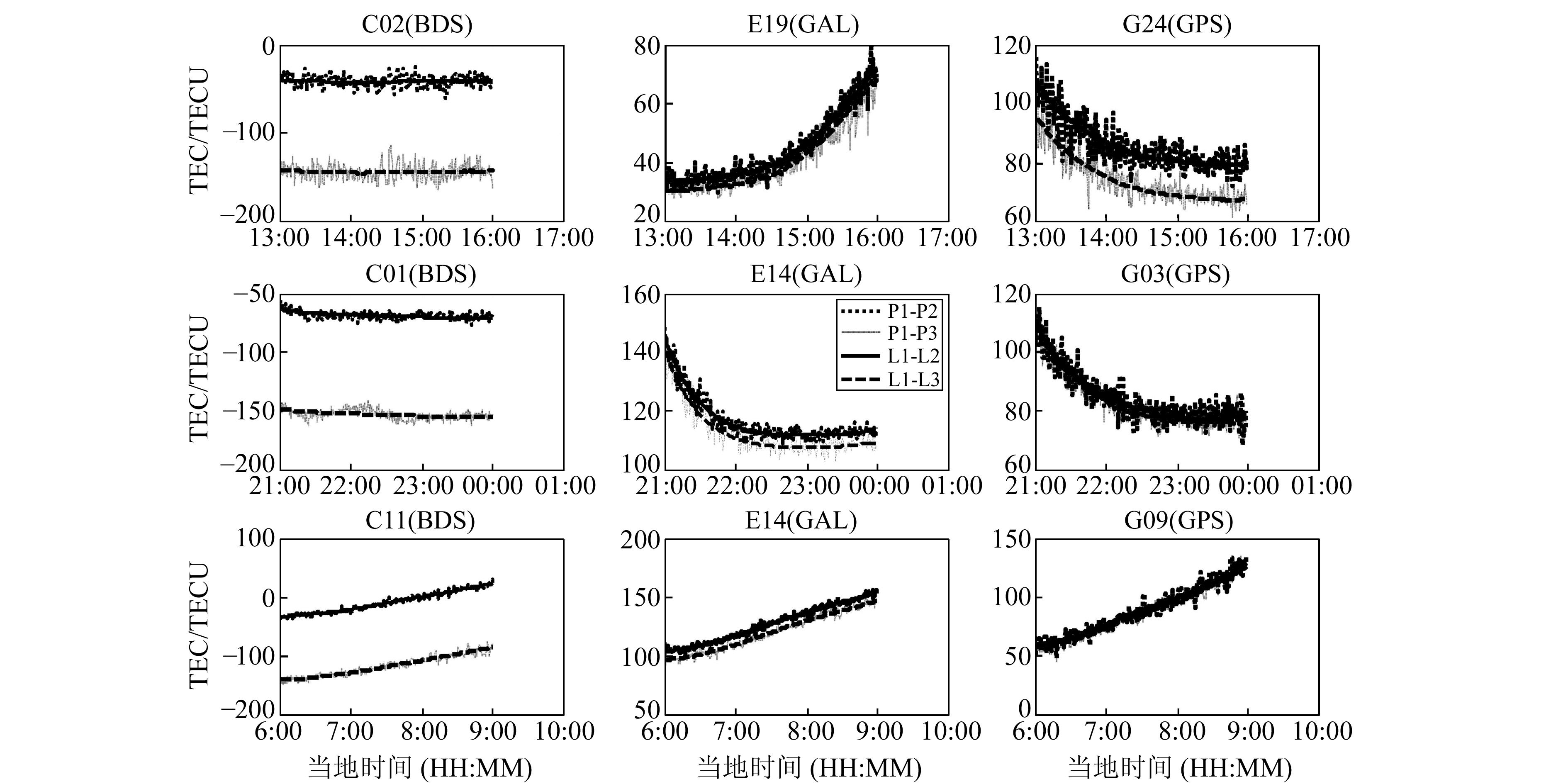
图 1为各测站未加入硬件延迟偏差改正的TEC曲线图。其中“P1-P2”、“P1-P3”分别代表使用f1、f2频率组合和f1、f3频率组合伪距观测值计算的TEC曲线,“L1-L2”、“L1-L3”分别为对应频率组合经过载波相位观测值平滑后的TEC曲线。从图中可以看出,由于伪距观测值噪声较大,导致由此计算得出的TEC曲线有着较大的波动,利用载波相位观测值可以对其进行很好的平滑,能较好地反映TEC曲线的总体变化趋势。各卫星不同频率组合TEC曲线变化情况大体一致,且曲线之间存在一个较为明显的系统差值。其中BDS卫星的这个偏差明显大于Galileo和GPS。此外,图 1中BDS卫星计算得出的TEC曲线出现负值情况,这也是由于未进行硬件延迟偏差改正导致的。
|
图 1 各测站(从上往下依次为ONS1、JFNG、NKLG测站)未加入硬件延迟偏差改正的TEC曲线 Fig. 1 TEC curves without hardware delay corrections (from top to bottom: ONS1, JFNG, NKLG) |
图 2为利用公式(4)计算所得的各测站各卫星频间硬件延迟偏差之差图。可以看出,由伪距观测值计算所得的各系统硬件延迟偏差之差存在轻微的波动,但总体上基本保持稳定,其值趋于某一常数。这表明在短时间内硬件延迟偏差是稳定的,因而使用不同频率组合获得的TEC曲线具有良好的一致性。本次实验中,BDS、Galileo、GPS 3个系统硬件延迟偏差之差的标准差范围分别为0.28~0.57 m、0.28~0.37 m、0.39~0.42 m。既然硬件延迟偏差短期内保持稳定,就可以利用IGS提供的每天一个硬件延迟偏差值进行改正。

|
图 2 各测站各卫星频间硬件延迟偏差之差曲线 Fig. 2 Thecurve of hardware delay deviation differences between frequencies for different satellites and stations |
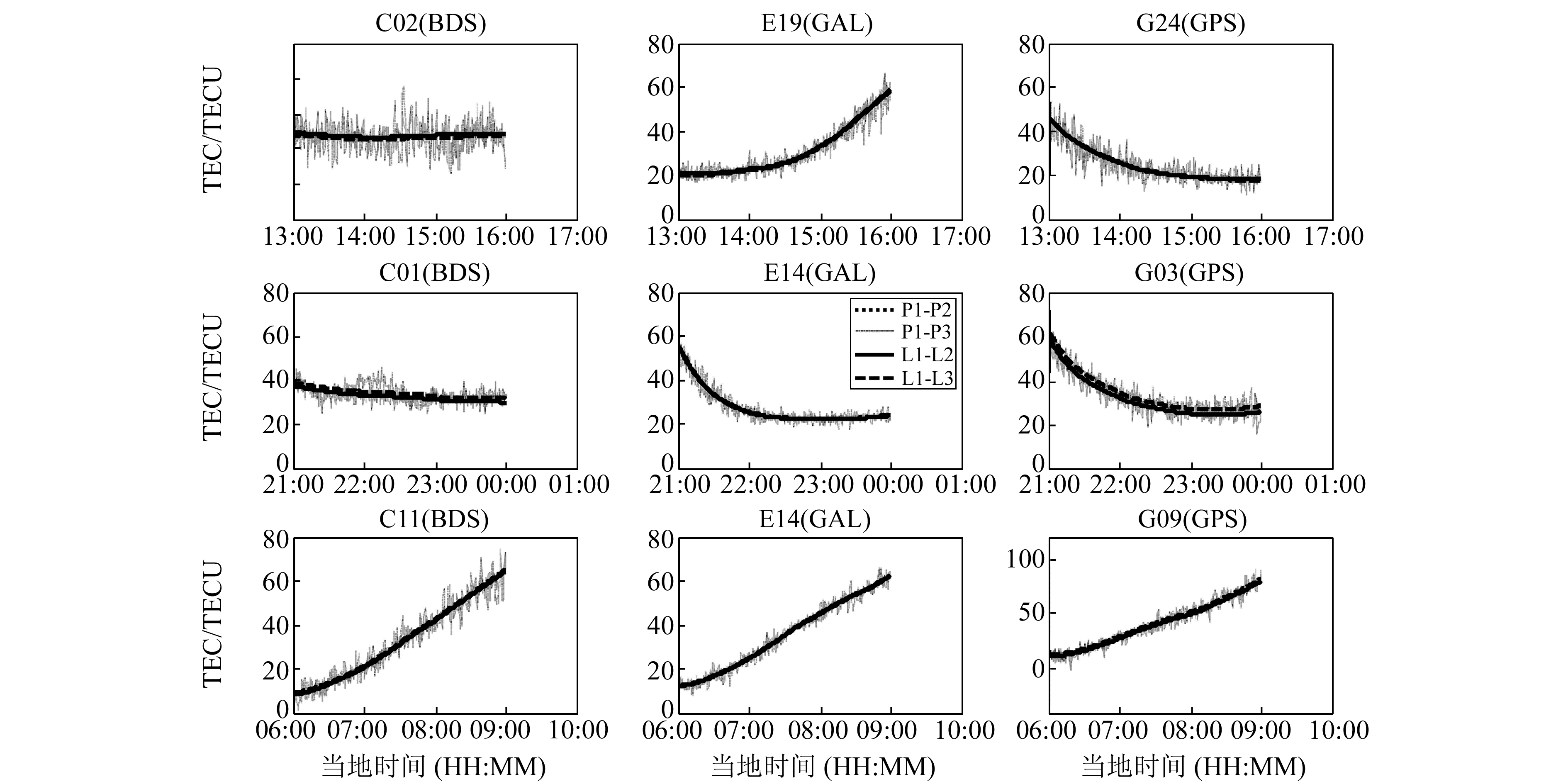
图 3为各测站加入IGS硬件延迟偏差的TEC曲线图。可以看出,除JFNG测站G03卫星,加入硬件延迟偏差后,各系统各卫星的两组频率数据计算的TEC曲线偏差值均有明显缩小,且TEC值均为正值。其中,BDS卫星由于含有较大的硬件延迟偏差,其缩小幅度最大。尽管如此,由于IGS网站DCB产品本身的精度限制,从图 3中还是能看出两条TEC曲线。
|
图 3 各测站(从上往下依次为ONS1、JFNG、NKLG测站)加入硬件延迟偏差改正的TEC曲线 Fig. 3 TEC curvewith hardware delay corrections (from top to bottom: ONS1, JFNG, NKLG) |
在图 3的基础上,利用公式(9)计算得到最终的TEC值。由于篇幅所限,本文只列举JFNG测站加入硬件延迟偏差的TEC值统计表(见表 3,单位TECu)。表头中的数字表示观测时段中的当地时间。从表中统计数据可以看出,加入硬件延迟偏差改正后,两组双频数据计算的TEC曲线之间相隔很小,但最大还能达到3 TECu(如G03卫星)。利用本文的方法,经过加权平均后能获得唯一的TEC结果。需要说明的是,在存在多路径误差与载波相位观测值发生周跳的情况下,不能直接应用本文的方法计算TEC,在计算TEC之前需要消除多路径误差和修复周跳。
|
|
表 3 JFNG测站三频数据计算获得的TEC最终结果 Tab. 3 Final TEC results using triple-frequency observations at JFNG station |
GNSS多系统多频信号为用户提供了更为丰富的观测数据,为电离层TEC监测提供了更多的冗余观测。本文充分利用GNSS三频伪距观测值及载波观测值,并结合IGS提供的硬件延迟偏差产品,对加入硬件延迟偏差前后的TEC曲线进行了对比。利用GPS、BDS、Galileo 3个IGS测站的卫星观测数据分析了硬件延迟偏差对计算电离层TEC的影响,结果表明,在硬件延迟偏差改正前,不同频率组合计算得到的TEC值存在明显的偏差,应用硬件延迟偏差改正后,该偏差值明显缩小。在分析伪距观测值精度与IGS硬件延迟产品精度的基础上,提出了一种利用GNSS三频数据计算TEC的方法。该方法通过加权平均,能得到唯一的TEC计算结果。
| [1] |
李征航, 黄劲松. GPS测量与数据处理[M]. 武汉: 武汉大学出版社, 2005 (Li Zhenghang, Huang Jinsong. GPS Surveying and Data Processing[M]. Wuhan: Wuhan University Press, 2005)
(  0) 0) |
| [2] |
刘瑞源, 吴健, 张北辰. 电离层天气预报研究进展[J]. 电波科学学报, 2004(增刊): 35-40 (Liu Ruiyuan, Wu Jian, Zhang Beichen. Development on Ionospheric Weather Prediction[J]. Chinese Journal of Radio Science, 2004(S1): 35-40)
(  0) 0) |
| [3] |
祝芙英, 吴云, 林剑, 等. 汶川Ms 8.0地震前电离层TEC异常分析[J]. 大地测量与地球动力学, 2008, 28(6): 16-21 (Zhu Fuying, Wu Yun, Lin Jian, et al. Study on Ionospheric TEC Anomaly Prior to Wenchuan Ms 8.0 Earthquake[J]. Journal of Geodesy and Geodynamics, 2008, 28(6): 16-21)
(  0) 0) |
| [4] |
吴云, 乔学军, 周义炎. 利用地基GPS探测震前电离层TEC异常[J]. 大地测量与地球动力学, 2005, 25(2): 36-40 (Wu Yun, Qiao Xuejun, Zhou Yiyan. Preseismic Ionospheric TEC Anomaly Detected by Ground-Based GPS[J]. Journal of Geodesy and Geodynamics, 2005, 25(2): 36-40)
(  0) 0) |
| [5] |
蔡昌盛, 李征航, 赵晓峰. 利用GPS组合观测值建立区域电离层模型研究[J]. 测绘工程, 2003, 12(1): 13-16 (Cai Changsheng, Li Zhenghang, Zhao Xiaofeng. Study on Regional Ionospheric Model Using GPS Combination Observations[J]. Engineering of Surveying and Mapping, 2003, 12(1): 13-16 DOI:10.3969/j.issn.1006-7949.2003.01.004)
(  0) 0) |
| [6] |
聂文锋, 胡伍生, 潘树国, 等. 利用GPS双频数据进行区域电离层TEC提取[J]. 武汉大学学报:信息科学版, 2014, 39(9): 1022-1027 (Nie Wenfeng, Hu Wusheng, Pan Shuguo, et al. Extraction of Regional Ionospheric TEC from GPS Dual Observation[J]. Geomatics and Information Science of Wuhan University, 2014, 39(9): 1022-1027)
(  0) 0) |
| [7] |
王晓岚, 马冠一. 基于双频GPS观测的电离层TEC与硬件延迟反演方法[J]. 空间科学学报, 2014, 34(2): 168-179 (Wang Xiaolan, Ma Guanyi. Derivation of TEC and GPS Hardware Delay Based on Dual-Frequency GPS Observations[J]. Chinese Journal of Space Science, 2014, 34(2): 168-179)
(  0) 0) |
| [8] |
Spits J, Warnant R. Total Electron Content Monitoring Using Triple Frequency GNSS: Results with Giove-A/-B Data[J]. Advances in Space Research, 2011, 47(2): 296-303 DOI:10.1016/j.asr.2010.08.027
(  0) 0) |
| [9] |
蔡昌盛, 李征航, 张小红. 利用GPS载波相位观测值建立区域电离层模型研究[J]. 测绘通报, 2002(11): 14-16 (Cai Changsheng, Li Zhenghang, Zhang Xiaohong. A Study of Regional Ionospheric Model Using GPS Carrier Phase Observations[J]. Bulletin of Surveying and Mapping, 2002(11): 14-16 DOI:10.3969/j.issn.0494-0911.2002.11.005)
(  0) 0) |
| [10] |
孙正明, 王坚, 高井祥. 利用双频GPS数据研究区域电离层TEC变化规律[J]. 测绘科学技术学报, 2008, 25(3): 199-201 (Sun Zhengming, Wang Jian, Gao Jingxiang. Variation Law of Regional Ionospheric TEC Using Dual-Frequency GPS Measurements[J]. Journal of Geomatics Science and Technology, 2008, 25(3): 199-201)
(  0) 0) |
 2017, Vol. 37
2017, Vol. 37




