2. 中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室, 武汉市徐东大街340号, 430077;
3. 中国科学院大学, 北京市玉泉路甲19号, 100049
大气折射效应是无线电测量系统中不可忽视的误差源之一。获取传播路径上高精度的对流层折射指数,对于无线电测量数据的误差修正有着至关重要的作用。现今国内外学者在对流层折射指数剖面获取方法方面进行了大量的研究,常见的基于地面气象参数的折射指数剖面模型[1]主要包括线性模型(地面至地面以上1 km)、指数模型[2]、分段模型、双指数模型[3]以及Hopfield模型[4]等。其中,Hopfield模型(又称双四次方折射指数模型)得到的折射指数剖面与真实情况更为贴近。陈祥明等[5-6]利用测站历史探空数据,建立了改进参数的折射率剖面模型;朱庆林[7-8]基于单站地基GNSS的电波折射,给出了低仰角对流层斜延迟实时折射率剖面的方法,并以汕头地区历史探空数据建立反演模型,给出相应的仿真结果;林乐科[1, 9]利用青岛地区1986~1995年的历史探空仪数据建立了基于地面测站气象元素以及ZTD的折射指数剖面反演模型,发现其优于Hopfield剖面反演模型。然而,完全基于探空数据建立反演模型也存在一定的缺陷,如在利用探空数据计算测站ZTD时,需要选择合适的计算模型以减少误差影响。另外,探空数据是通过探空气球把无线电探空仪携带到高空来测定气象参数而获取的,由于探空气球到达的高度有限,且一天仅进行两次数据观测,而GNSS观测数据是通过卫星信号实时获取的。相比之下,利用探空数据获取的ZTD在时空分辨率上存在一定的不足。本文提出一种基于GNSS观测数据计算高精度ZTD以代替探空数据计算ZTD数据的对流层折射指数剖面反演模型方法,以下简称为新模型。并利用了BJFS、WUHN、WIND(纳米比亚首都)和DARW(澳大利亚港市)4个测站2011~2014年的探空仪数据以及对应测站GNSS数据计算的ZTD值进行相应处理分析,以验证新模型的对流层折射指数剖面反演精度。
1 基于GNSS及探空仪数据的大气折射指数剖面反演模型方法的原理本文采用与文献[1]相类似的反演建模方法,将12 km以下的大气按每层500 m的高度进行分层,并基于测站地面的温度、水汽压和ZTD,在各层建立剖面反演模型[1]。其新模型方程如下表示:
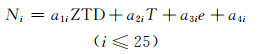
|
(1) |
式中, Ni为第i高度层的大气折射指数,a1i、a2i、a3i、a4i表示对应第i高度层的反演模型系数值,这里大气折射指数以及反演模型系数都是无量纲量;ZTD为测站天顶对流层延迟,利用GNSS数据计算,单位为m;T和e分别为测站地面的温度和水汽压,从探空仪数据中获取,单位为绝对温度K和hPa。
首先,根据Smith和Weintranb给出的公式可知[10],给定精确的气象数据就可以求出精确的大气折射指数N值。本文认为,经过对探空仪数据的预处理,由探空仪数据得到的每个高度层处的气象数据是正确的,那么利用2011~2014年的探空仪气象数据,求出探空气球在其停留高度处的大气折射指数N值,就可以认为是精确的。其具体计算公式如下:
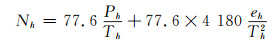
|
(2) |
式中, Ph、Th和eh分别代表探空气球在其停留高度处的大气压、温度和水汽压,Nh为对应高度处计算的大气折射指数。由于探空气球的停留高度一般不会与分层高度一样,因此需要通过适当的插值方法得到分层高度处的大气折射指数N值。通过分析大量的数据发现,N值的高度分布近似为指数分布,因此文中对求出的N值先取自然对数,然后利用线性插值方法得到反演模型分层高度处的N值,这样通过插值方法得到的N值基本上可以认为是正确的。
基于探空仪数据反演模型中的ZTD值则利用式(3)计算[11],相应的地面温度和水汽压与式(1)相同,均从探空气象数据中获得:
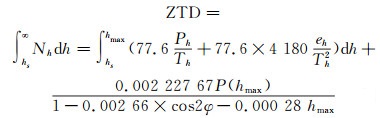
|
(3) |
式中, h为高度,hs为地面高度,hmax为探空气球所达到的最高高度,单位均为m。Ph、Th和eh分别代表探空气球在其停留高度处的大气压、温度和水汽压;P(hmax)为探空气球所达到的最高高度处的大气压强,单位为hPa;φ为探空测站处的纬度,单位为rad。基于探空仪数据反演模型,使用文献[1]提出的一种大气折射指数反演模型,其精度较好,且优于Hopfield模型。本文计算的新模型将与此反演模型(下文简称为探空数据反演模型)进行比较分析。
首先,以2011~2013年探空仪数据中的气象数据以及GNSS测站数据计算的ZTD值建立新模型;然后,以2014年探空仪数据中的气象数据以及GNSS测站数据计算的ZTD值来验证新模型的精度;同时,对比分析新模型计算对流层折射指数与基于探空数据反演模型、Hopfield模型计算结果的差异。方案的具体实现步骤为:选取同时具有探空气象数据和GNSS数据的测站,对探空仪数据进行预处理得到探空测站的气象参数;利用适当插值方法计算反演模型分层高度处的N值,相应GNSS测站的ZTD值通过IGS提供;先结合2011~2013年的数据建立的新反演模型,然后以2014年数据验证新模型的精度。方案实施的流程图如图 1所示。
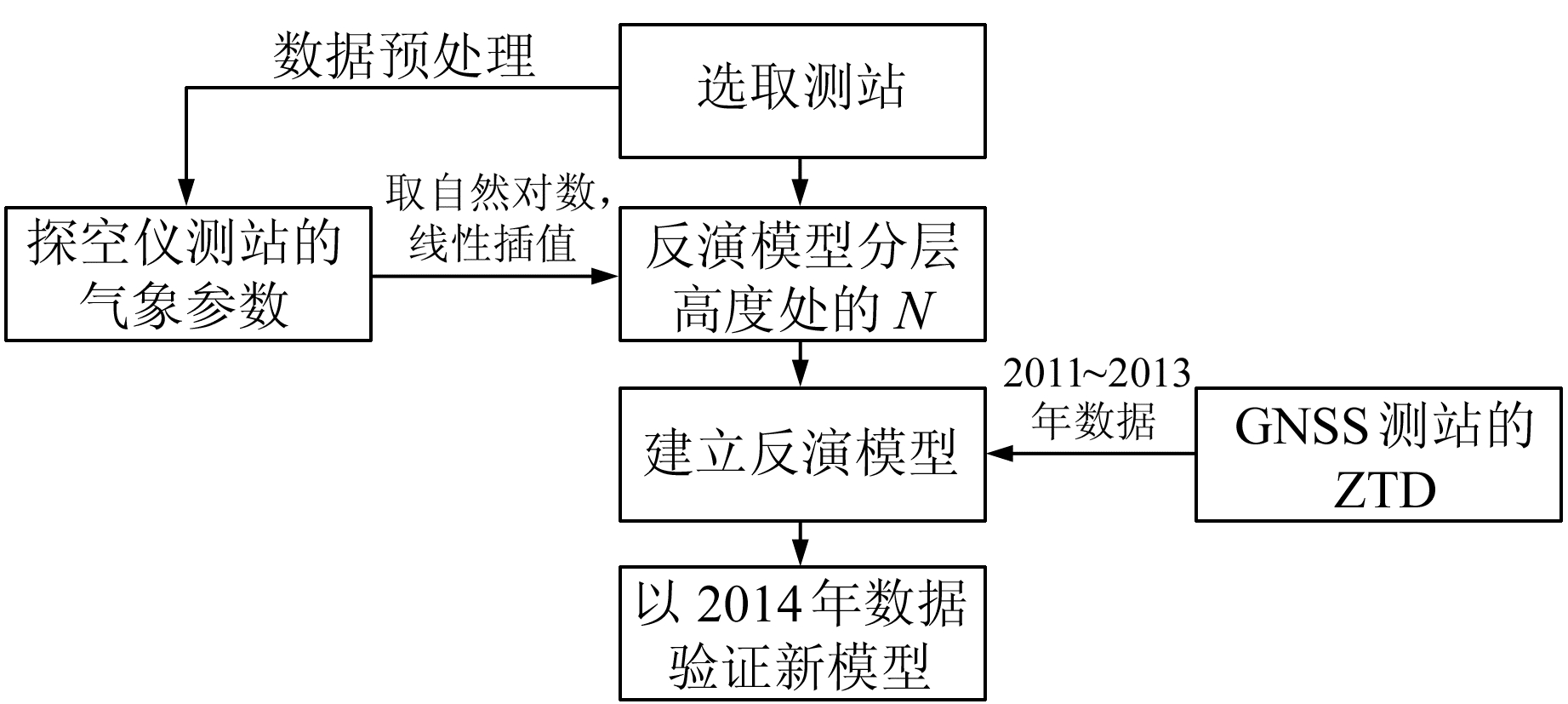
|
图 1 新模型的实现步骤 Fig. 1 Implementation steps of new model |
由于BJFS与WUHN有着不同的气候、地理特征,它们可以代表国内不同区域的研究结果,而WIND和DARW是国外的2个站,这2个站也有着不同的地理概貌、海拔、气候等,因此本文利用BJFS、WUHN、WIND以及DARW的数据进行相应的处理分析。需要说明的是,由于没有严格意义上的并置观测数据,此处4个测站的探空仪测站位置与GNSS测站位置相距一定距离。其中,GNSS测站为探空仪测站附近的IGS连续跟踪站,相应GNSS测站的ZTD值则直接采用IGS提供的ZTD值(可从ftp://cddis.gsfc.nasa.gov/gnss/网站上获取,也可以通过PPP技术自行解算)。而探空仪测站的探空气象数据则从ftp://ftp.ncdc.noaa.gov/pub/data/igra/derived-v2/data-por/网站上获取。表 1为探空仪测站与IGS测站之间的位置信息。
|
|
表 1 探空仪测站和IGS测站的位置信息 Tab. 1 Location information about radiosonde station and IGS station |
从表 1可以看出,探空仪测站和IGS测站的平面距离最大在30 km左右,高程差异最大在96 m左右,如不考虑特殊情况,ZTD在几十km的小区域范围内变化很小[12],因此本文可以假设IGS测站计算的ZTD基本上是探空仪测站附近的ZTD值。
首先根据最小二乘法,利用2011~2013年的探空仪气象数据以及IGS测站的ZTD值分别计算新模型以及基于探空仪数据反演模型的系数值,并比较这两种模型的结果;然后以2014年数据进行反演模型的验证:利用式(4),计算每层反演模型的RMSE[13],并将这两种反演模型的验证结果与Hopfield模型进行比较:
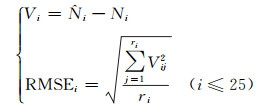
|
(4) |
式中, 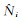
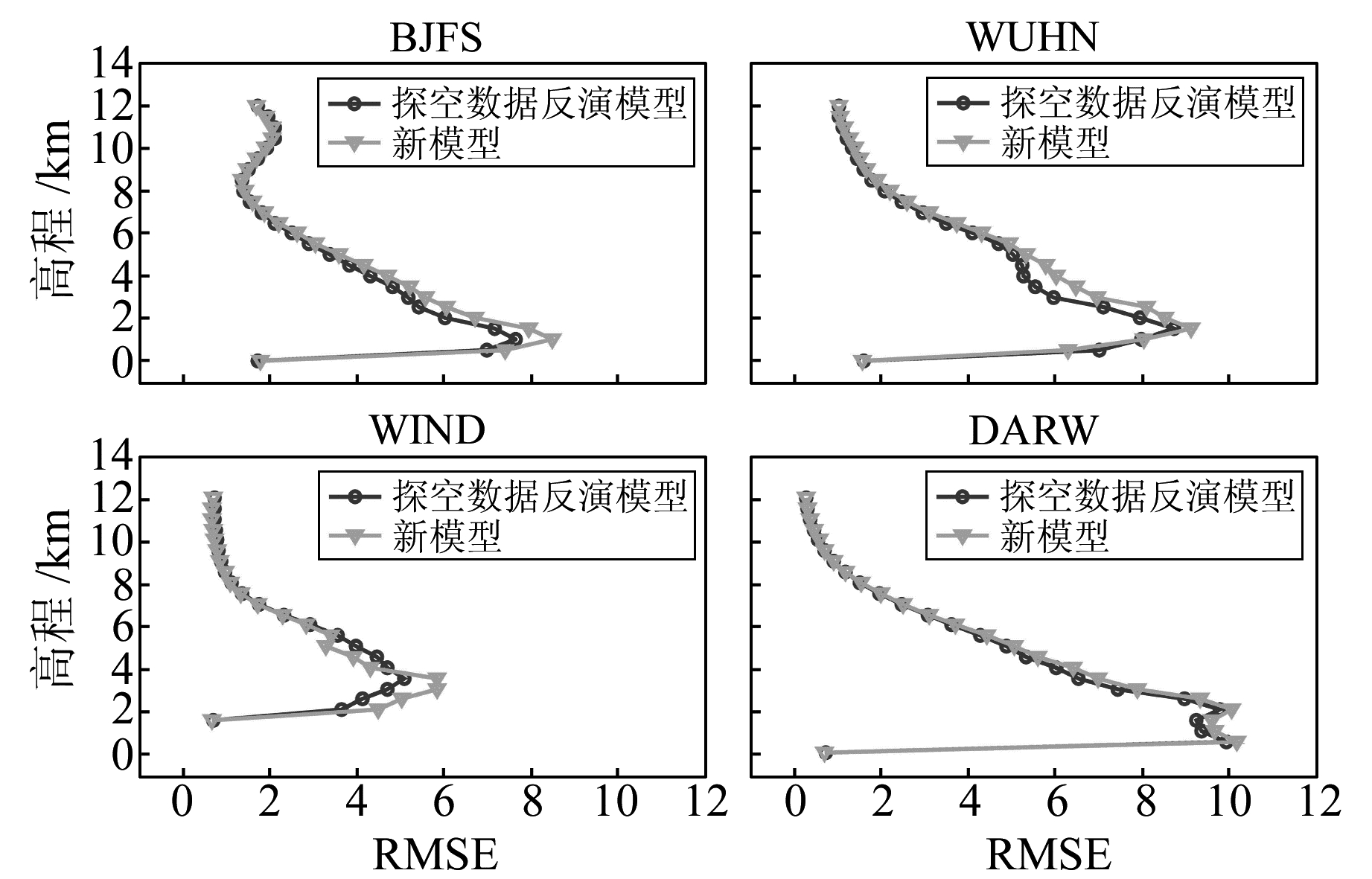
本文利用C++编制了相应的数据处理软件,计算并验证了模型在BJFS、WUHN、WIND以及DARW上的精度。其中,这4个站分别使用了1 725个、1 305个、381个和1 990个数据样本进行模型建模以及418个、378个、37个和696个数据样本进行模型验证。由于WIND探空仪数据和ZTD数据匹配得较差,故该台使用的样本数较少。具体结果详见图 2~5,其中图 2是新模型与探空数据反演模型的模型精度比较结果,图 3是不同反演模型的验证结果。考虑到篇幅限制,本文以其中两个站为例,给出新模型在这两个站上的偏差变化,具体结果如图 4、图 5所示。
|
图 2 基于探空仪数据反演模型与新模型的精度比较 Fig. 2 Comparison between model accuracies of inversion model based on radiosonde data and new model |

|
图 3 3种不同反演模型的验证结果比较 Fig. 3 Comparison among validation results for three kinds of different inversion models |
|
图 4 利用新模型计算的BJFS各层折射指数偏差值 Fig. 4 Refractive index deviation in each layer calculated by new model in BJFS |
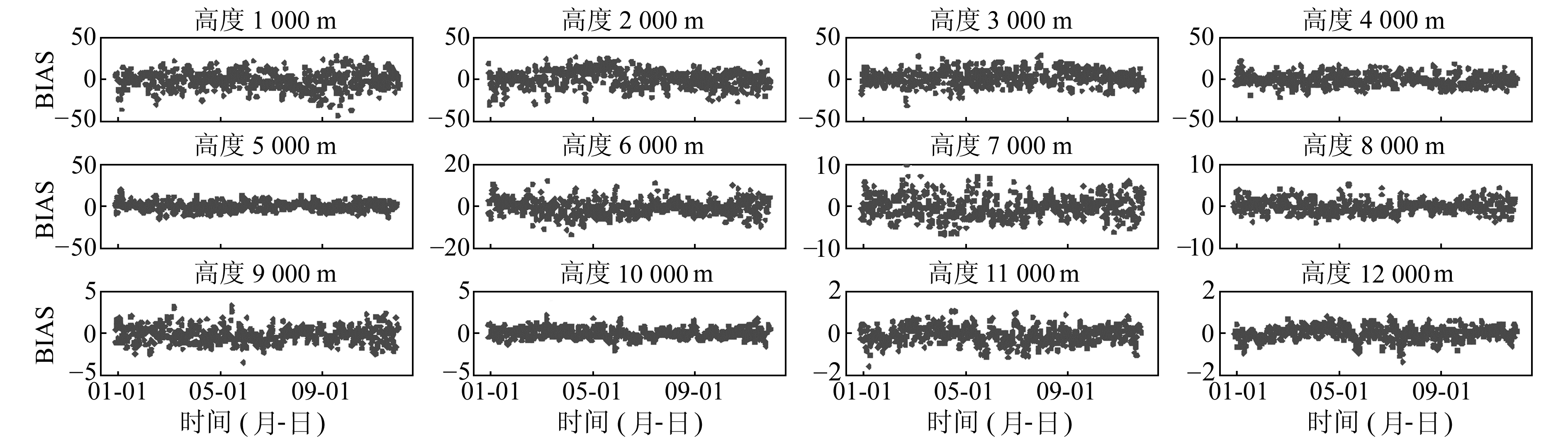
|
图 5 利用新模型计算的WUHN各层折射指数偏差值 Fig. 5 Refractive index deviation in each layer calculated by new model at WUHN |
从以上实验结果可以看出:
1) 图 2中结果表明,新模型与基于探空仪数据建立的反演模型精度相当。其中,在只有少量数据的WIND站,新模型与探空数据反演模型的吻合度稍显不足,但是从图 3的各个反演模型的验证结果来看,新模型在WIND中的精度与探空数据的反演模型相差不大。这说明利用少量数据建立的新模型同样也能达到与基于探空数据的反演模型相当的精度。
2) 从图 3中可以看出,与Hopfield模型相比,新模型具有较好的反演精度,特别是在分层高度位于2~6 km时,二者精度差异较为明显。
3) 从图 4~5可以看出,利用新模型计算的测站各层折射指数偏差在0值附近上下波动,不存在明显的系统偏差。同时,各测站分层高度在5 km以上时,利用新模型计算各层折射指数偏差值绝对值基本上保持在10以内,且随着高度增加,其偏差值越小;分层高度在5 km以下时,偏差值绝对值基本上保持在20以内,只有少数偏差的绝对值大于20。
3 结语本文结合GNSS数据计算ZTD以及探空仪数据的气象数据,建立了一种新的ZTD反演模型。以BJFS、WUHN、WIND以及DARW为例进行计算,验证了模型的精度。结果表明,新的ZTD反演模型与基于探空数据的反演模型精度相当。新模型利用GNSS数据,直接采用参数估计计算ZTD,相比于利用式(3)采用近似模型计算而言,具有较高的精度及可靠性。在实际应用新模型时,可以在实验测站附近架设GNSS接收机,然后根据观测值文件,采用PPP技术直接计算测站ZTD值,并利用气象采集设备测量同时刻地面处的温度与水汽压;最后利用新的ZTD反演模型来反演大气分层高度处的大气折射指数。
| [1] |
林乐科.利用GNSS信号的地基大气折射率剖面反演技术研究[D].南京: 南京邮电大学, 2011 (Lin Leke. Profiling Tropospheric Refractivity Based on Single Ground-Based GPS Receiver[D]. Nanjing: Nanjing University of Posts and Telecommunications, 2011) http://cdmd.cnki.com.cn/Article/CDMD-10293-1012276092.htm
(  0) 0) |
| [2] |
Bean B R, Thayer G D. Models of the Atmospheric Radio Refractive Index[C].ⅡE, 1959
(  0) 0) |
| [3] |
Bean B R. Double Model of Radio Wave Refractivity in the Troposphere[J]. Beitr Phys Atmosph, 1961, 34(1-2): 81-91
(  0) 0) |
| [4] |
Hopfield H S. Two-Quartic Tropospheric Refractivity Profile for Correcting Satellite Data[J]. Journal of Geophysical Research, 1969, 74(18): 4487-4499 DOI:10.1029/JC074i018p04487
(  0) 0) |
| [5] |
Davis J L, Herring T A, Shapiro I I, et al. Geodesy by Radio Interferometry: Effects of Atmospheric Modeling Errors on Estimates of Baseline Length[J]. Radio Sci, 1985, 20: 1593-1607 DOI:10.1029/RS020i006p01593
(  0) 0) |
| [6] |
Lowry A R, Rocken C, Sokolovskiy S V, et al. Vertical Profiling of Atmospheric Refractivity from Ground-Based GPS[J]. Radio Sci, 2002, 37(3): 13-19
(  0) 0) |
| [7] |
朱庆林.基于单站地基GNSS的电波折射参数估计[D].西安: 西安电子科技大学, 2010 (Zhu Qinglin. Estimation of Electromagnetic Wave Refraction Parameters by Singular Ground-based GNSS[D]. Xi'an: Xidian University, 2010) http://cdmd.cnki.com.cn/Article/CDMD-10701-2010128547.htm
(  0) 0) |
| [8] |
朱庆林, 赵振维, 林乐科, 等. 单站地基GPS实时估计电波折射弯曲角[J]. 武汉大学学报:信息科学版, 2012(6): 671-674 (Zhu Qinglin, Zhao Zhenwei, Lin Leke, et al. Real Time Estimation of Electromagnetic Wave Refraction Bending Angles with Singular Ground-Based GPS[J]. Geomatics and Information Science of Wuhan University, 2012(6): 671-674)
(  0) 0) |
| [9] |
Bevis M, Businger S, Herring T A, et al. GPS Meteorology: Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System[J]. Journal of Geophysics Research, 1992, 97(D14): 15787-15801 DOI:10.1029/92JD01517
(  0) 0) |
| [10] |
Bean B R, Dutton E J. Radio Meteorology[M]. New York: Dover Publications, 1968
(  0) 0) |
| [11] |
Saastamoinen J. Contribution to the Theory of Atmospheric Refraction[J]. Bulletin Geodesique, 1973, 107: 13-34 DOI:10.1007/BF02522083
(  0) 0) |
| [12] |
戴吾蛟, 陈招华, 匡翠林, 等. 区域精密对流层延迟建模[J]. 武汉大学学报:信息科学版, 2011(4): 392-396 (Dai Wujiao, Chen Zhaohua, Kuang Cuilin, et al. Modeling Regional Precise Tropospheric Delay[J]. Geomatics and Information Science of Wuhan University, 2011(4): 392-396)
(  0) 0) |
| [13] |
Wu Y Y, Hong Z J, Guo P, et al. Simulation of Atmospheric Refractive Profile Retrieving from Low-Elevation Ground-Based GPS Observations[J]. Chinese Journal of Geophysics, 2010, 53(4): 639-645 DOI:10.1002/cjg2.v53.4
(  0) 0) |
2. State Key Laboratory of Geodesy and Earth's Dynamics, Institute of Geodesy and Geophysics, CAS, 340 Xudong Street, Wuhan 430077, China;
3. University of Chinese Academy of Sciences, A19 Yuquan Road, Beijing 100049, China
 2017, Vol. 37
2017, Vol. 37


