GNSS基线解算主要采用最小二乘方法,其数学模型(Gauss-Markov模型)分为函数模型和随机模型。为了得到高精度解算结果,这2种模型均需准确确定。GNSS观测量之间存在着物理相关性、空间相关性、时间相关性及方差不等性[1-2],随机模型即要描述这些特性。常用的随机模型主要包括等权模型、经验模型和验后估计模型。近代平差理论中提出的验后估计,也称为方差分量估计(variance component estimation, VCE),是通过平差后得到的残差信息来估计观测量的方差(协方差),代表性方法有最小范数二次无偏估计(minimum norm quadratic unbiased estimator, MINQUE)、最优不变二次无偏估计(best invariant quadratic unbiased estimator, BIQUE)、约束最大似然估计(restricted maximum likelihood, REML)和最小二乘方差分量估计[3-4] (least-squares variance component estimation, LS-VCE)。经验模型一般比较简单,使用方便,适用于动态和静态定位,但该模型与接收机和观测环境相关,且实际模型的选择缺乏更严谨的理论依据。验后估计是一种严密的估计算法,通过迭代运算,可估计出各类受到不同因素影响的观测值的单位权方差因子,因此验后估计需要较多的冗余观测量,计算量大,一般适用于静态和快速静态定位。
本文将上述2种精化方法相结合,采用LS-VCE方法对卫星高度角模型中的未知参数进行估计,得到更符合实际的随机模型,并使用某矿区的GPS观测数据予以验证。
1 卫星高度角模型精化方法 1.1 LS-VCE基本原理LS-VCE方法最初由Teunissen提出,之后由Teunissen,Amiri-Simkooei等人完善。该VCE方法基于经典的最小二乘理论,使用起来灵活方便,允许自定义权阵,可以获得方差(协方差)的最小方差估计量及其估计精度,同时可以使用假设检验,如w-test、v-test来判断所获得的随机模型的正确性[5-6]。
LS-VCE利用矩阵半拉直运算将随机模型转换为Gauss-Markov模型中函数模型的形式,从而使用最小二乘法对随机模型中的未知参数,即方差(协方差)分量进行估计。本文简要地给出LS-VCE计算公式[3]。
观测量的线性观测方程为:
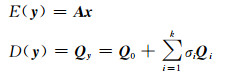
|
(1) |
式中,y为观测值向量,x为未知数向量,A为设计矩阵,Qy为观测量的方差(协方差)阵,k为观测量的分类数,Q0, Q1, …, Qk为已知的协因数阵,σ1, …, σk为待估计的方差(协方差),E、D分别表示求期望和方差运算。
LS-VCE得到的方差(协方差)估计值为:
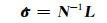
|
(2) |
式中,N是一个k×k矩阵,其元素为:
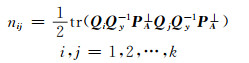
|
(3) |
式中,L是一个k×1向量,其元素为:
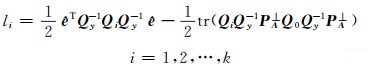
|
(4) |
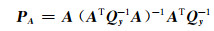
|
(5) |
式中,I为单位阵。残差为:
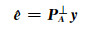
|
(6) |
给定σ1, …, σk的初始值,使用循环迭代方法计算
GPS基线解算一般采用双差观测量构成其数学模型,本文给出单频双差观测的方差(协方差)阵。
设i、j两个测站在历元t同步观测了m颗卫星,认为不同测站对同一颗卫星的观测精度相同,即σs2=σφis2=σφjs2,s=1, 2, …,m,则i、j两个测站原始观测量在历元t的方差阵可简化表示为:
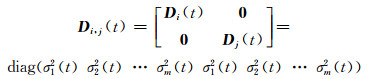
|
(7) |
根据误差传播定律,得到历元t双差观测量的方差(协方差)阵:
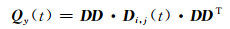
|
(8) |

|
(9) |
不考虑观测量历元间的相关性,根据式(8)得到n个观测历元t1, …, tn,双差观测量的方差阵:

|
(10) |
原始观测量的方差可用卫星高度角的函数表示:
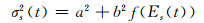
|
(11) |
式中,Es(t)为卫星s在历元t的高度角,f为某种函数,a、b为待定系数。
将式(11)代入式(7)中:

|
(12) |
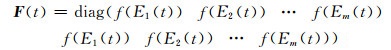
|
(13) |
所以,历元t双差观测量的方差(协方差)阵为:
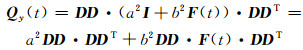
|
(14) |
令
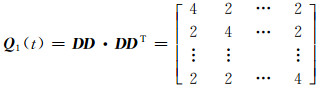
|
(15) |
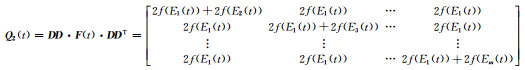
|
(16) |
对于n个观测历元,有:

|
(17) |
可以看出,式(17)即为式(1)中随机模型的形式(k=2),可使用LS-VCE方法求出系数a2、b2的估值,继而确定基线双差解算的权阵。
卫星高度角模型中的函数f的确定,目前一般可分为2类。
1) 指数模型[7]:
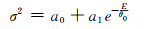
|
(18) |
式中,a0、a1、θ0为系数,E为卫星高度角。
指数模型中的系数与接收机和观测量类型有关,可根据实际观测值非线性拟合获得。更为严谨的,可通过验后估计方法求出其估值。
2) 三角函数模型:
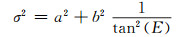
|
(19) |
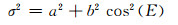
|
(20) |
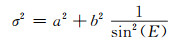
|
(21) |
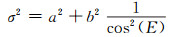
|
(22) |
式中,a、b为系数,E为卫星高度角。
模型(19)[8]是根据电离层延迟公式和Hopfield对流层延迟改正模型,适当调整模型(21)得出的,其中a取0,b取1;Bernese软件使用模型(20)[9],其中a取0,b取1;GAMIT软件使用模型(21)[10],其中a=4.3 mm,b=7 mm;模型(22)由文献[11]提出。
2 模型的实验分析 2.1 数据来源实验数据选取2012年某矿区GPS控制网中的1条基线(基线长度10.6 km),接收机为Trimble R8,静态观测1 h,采样间隔15 s,卫星截止高度角10°,同步观测10颗卫星,选择其中的5颗卫星进行算例分析。
2.2 实验分析使用自编的MATLAB程序,对L1载波相位静态观测数据利用LS-VCE方法估计出模型(18)~(22)中的系数,确定双差观测量的方差(协方差阵);之后使用等权模型、模型(18)、模型(19)、模型(20)分别进行基线解算,采用LAMBAD算法固定整周模糊度,将由控制网解算出的该基线向量解作为真值进行比较。
2.2.1 基于卫星高度角的随机模型系数求解为了提高解算精度和效率,需将多个历元的观测方程分组求解。
本文使用单频双差观测量线性化方程及LS-VCE方法对§1.3中提出的高度角模型系数进行估计,循环条件为:‖σfirst-σlast‖ < 10-6。对于指数模型(18),将θ0设为10°。
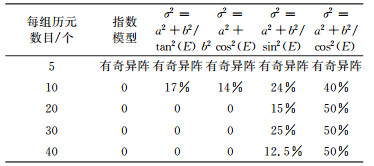
在求解过程中出现了方差为负的情况,统计结果见表 1。
|
|
表 1 模型系数估计方差为负的情况统计 Tab. 1 The statistic of negative variances |
造成负方差的原因主要有[12-13]:1)函数模型中没有足够的观测量;2)随机模型选取不当;3)方差(协方差)分量解算时,先验值不正确等。
从表 1可知,采用每组5个历元求解时所有模型在矩阵求逆时都出现了奇异矩阵,说明观测量不足;将观测历元增加至每组10个时,指数模型求出的方差值均为正;随着每组历元数的增加,σ2=a2+b2/tan2(E)、σ2=a2+b2cos2(E)模型消除了负方差;但对于σ2=a2+b2/sin2(E)、σ2=a2+b2/cos2(E)模型,每组历元数目达到40个以上时,仍有大量方差为负,且变换解算初始值也未起作用,说明这2种随机模型不适用于该观测数据的解算。
根据上述分析,对于前3种模型,当分组历元数目达到20个及以上时可估计出未知系数。对于每组20个历元,使用LS-VCE方法求解时循环迭代的平均次数分别为13.5、2.9、3.6,与表 2中每组30个历元的解算方案比较可知,后者的效率更高。观测量数量越多,估计值的可靠性越高,同时兼顾样本数量,本文采用每组30个历元的解算方案估计前3种模型中的未知系数,结果见表 2。
|
|
表 2 模型系数估计值 Tab. 2 The estimated values of model parameters |
通过LS-VCE估计出模型系数a、b之后,可代入式(17)中求出Qy,继而计算出基线向量的浮点解,经LAMBAD算法固定整周模糊度后得到基线向量的固定解。
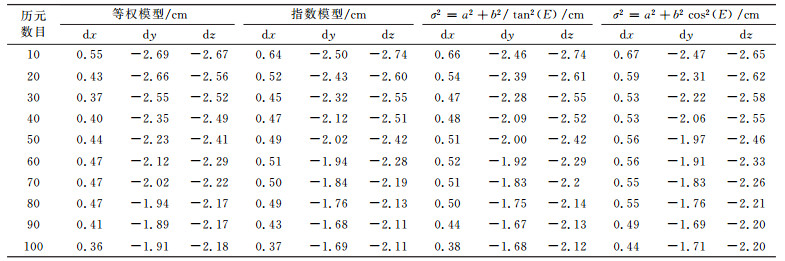
使用该基线的L1载波相位观测数据,分别按照等权模型和表 2中的3种模型进行双差基线解算。利用不同观测时间的数据,将4种模型计算得到的基线向量固定解与真值进行比较,结果见表 3。
|
|
表 3 不同随机模型解算结果较差 Tab. 3 The difference between baseline components of different stochastic models |
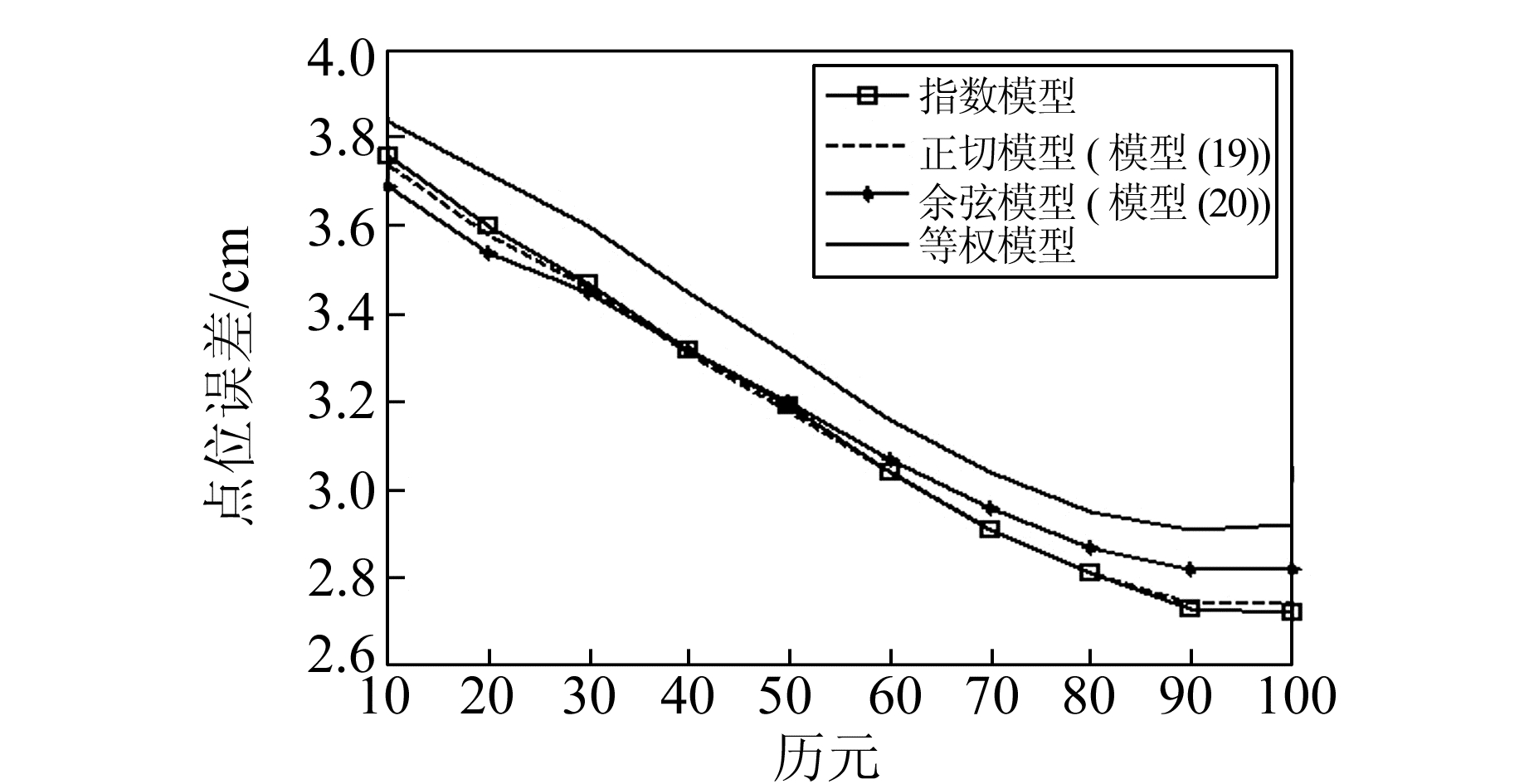
根据3个方向的较差算出点位误差,绘制曲线如图 1所示。
|
图 1 随机模型点位误差比较 Fig. 1 Comparison among positional errors of different stochastic models |
由图 1可看出:1)等权模型的计算精度最低;2)指数模型与正切模型解算精度相当,结合表 2的迭代次数可知,正切模型的解算效率更高;3)余弦模型在前30个历元解算精度最优,50个历元以后精度不及指数模型与正切模型。
3 结语随机模型的精化是获得高精度定位结果的关键,随机模型选取不恰当,不仅会降低解算精度,而且有可能导致错误的定位结果。本文通过自主编程实现了基于卫星高度角的随机模型参数的LS-VCE估计,采用负方差这一指标说明,σ2=a2+b2/sin2(E)和σ2=a2+b2/cos2(E)不适用于实际算例,为随机模型的选择提供了一定的理论依据。
通过与基线向量真值的较差比较可进一步分析出,σ2=a2+b2/tan2(E)的平均解算精度和效率最优。因此,在数据处理时应根据实际使用情况,合理地选择随机模型。
| [1] |
Luo X. GPS Stochastic Modelling Signal Quality Measures and ARMA Processes[D]. Karlsruhe: Karlsruhe Institute of Technology, 2012
(  0) 0) |
| [2] |
郭秋英. GPS快速精密定位数据处理[M]. 徐州: 中国矿业大学出版社, 2011 (Guo Qiuying. Research on Data Processing of GPS Rapid Precise Positioning[M]. Xuzhou: China University of Mining and Technology Press, 2011)
(  0) 0) |
| [3] |
Amiri-Simkooei A R. Least-Squares Variance Component Estimation: Theory and GPS Applications[D]. Delft: Delft University of Technology, 2007 http://xueshu.baidu.com/s?wd=paperuri%3A%2838a87799e0aa9430e8927385c09fca2a%29&filter=sc_long_sign&sc_ks_para=q%3DLeast-squares%20variance%20component%20estimation&sc_us=9425294339982230469&tn=SE_baiduxueshu_c1gjeupa&ie=utf-8
(  0) 0) |
| [4] |
Teunissen P J G, Amiri-Simkooei A R. Least-Squares Variance Component Estimation[J]. Journal of Geodesy, 2008, 82(2): 65-82 DOI:10.1007/s00190-007-0157-x
(  0) 0) |
| [5] |
Amiri-Simkooei A R, Zangeneh-Nejad F, Asgari J. Least-Squares Variance Component Estimation Applied to GPS Geometry-Based Observation Model[J]. Journal of Surveying Engineering, 2013, 139(4): 176-187 DOI:10.1061/(ASCE)SU.1943-5428.0000107
(  0) 0) |
| [6] |
Amiri-Simkooei A R, Ansari H, Sharifi M A. Application of Recursive Least Squares to Efficient Blunder Detection in Linear Models[J]. Journal of Geomatics Science and Technology, 2015, 5(2): 258-267
(  0) 0) |
| [7] |
Zangeneh-Nejad F, Amiri-Simkooei A R, Sharifi M A, et al. On the Realistic Stochastic Model of GPS Observables: Implementation and Performance[J]. The International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, 2015, 40(1): 755
(  0) 0) |
| [8] |
邱卫宁, 齐公玉, 邹进贵, 等. 不同随机模型在GPS单历元变形解算中的应用研究[J]. 测绘通报, 2011(10): 5-7 (Qiu Weining, Qi Gongyu, Zou Jingui, et al. Research on Different Stochastic Model in GPS Single Epoch Deformation Monitoring[J]. Bulletin of Surveying and Mapping, 2011(10): 5-7)
(  0) 0) |
| [9] |
Dach R, Lutz S, Walser P, et al. User Manual of the Bernese GNSS Software, Version 5.2[Z]. Switzerland: University of Bern, Bern Open Publishing, 2015
(  0) 0) |
| [10] |
Herring T A, King R W, Floyd M A, et al. Gamit Reference Manual: GPS Analysis at MIT Release 10.6[Z]. Cambridge MA: Dept of Earth, Atmospheric, and Planetary Sciences, MIT, 2015
(  0) 0) |
| [11] |
Jin S G, Wang J, Park P H. An Improvement of GPS Height Estimations: Stochastic Modeling[J]. Earth Planets & Space, 2005, 57(4): 253-259
(  0) 0) |
| [12] |
黄维彬. 近代平差理论及其应用[M]. 北京: 解放军出版社, 1997 (Huang Weibin. Theory and Application of Modern Surveying Adjustment[M]. Beijing: PLA Press, 1997)
(  0) 0) |
| [13] |
Amiri-Simkooei A R. Non-Negative Least-Squares Variance Component Estimation with Application to GPS Time Series[J]. Journal of Geodesy, 2016, 90(5): 451-466 DOI:10.1007/s00190-016-0886-9
(  0) 0) |
 2017, Vol. 37
2017, Vol. 37