2. 广西空间信息与测绘重点实验室,桂林市雁山街319号,541006;
3. 东海航海保障中心上海海事测绘中心,上海市共青路82弄7号,200086
在GNSS(global navigation satellite system)、VLBI(very long baseline interferometry)和DORIS(doppler orbitography by radiopositioning integrated on satellite)测量中,对流层斜路径延迟是一个很重要的误差源;在地基GPS水汽反演中,对流层延迟也是一个非常重要的参数。对流层斜路径延迟包括干延迟和湿延迟两个部分[1]:
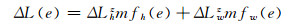
|
(1) |
式中,mfh(e)、mfw(e)分别为高度角为e处的干延迟和湿延迟的映射函数;ΔLhz、ΔLwz分别为天顶方向干延迟和湿延迟。天顶方向湿延迟ΔLwz通常作为参数进行估计[2-3],而天顶干延迟ΔLhz在静力学平衡条件下一般可用模型精确估计[4]。可见,映射函数准确与否决定了斜路径延迟的精度,进而影响GPS基线解算质量。因此,利用高精度的映射函数可以更准确地求出斜路径延迟,提高GPS数据处理结果的质量。
1 对流层延迟映射函数概述对流层延迟映射函数通常可以分为3类:第1类是Saastamoinen和Hopfield等经典映射函数;第2类是Ifadis、MTT、NMF等连分式形式的映射函数;第3类是动态映射函数,如VMF、GMF模型等。
1.1 尼尔映射函数(Niell mapping function, NMF)Niell A利用全球分布的26个无线电探空气球站的资料,采用美国标准大气模式中北纬15°、30°、45°、60°、75°的1月和7月的湿度和温度廓线得出了NMF模型[5]。映射函数包括干延迟映射函数mfh和湿延迟映射函数mfw两部分。NMF模型的干延迟映射函数mfh可表示为:

|
(2) |
式中,e为卫星高度角;H(e)为与测站高程有关的改正项;系数ah可按下式计算:
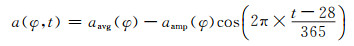
|
(3) |
式中,φ为纬度,t为年积日,aavg、aamp由文献[5]给出。bh、ch的计算方法与之相同。
NMF模型的湿延迟映射函数mfw可表示为:
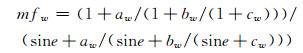
|
(4) |
式中的系数aw、bw、cw由文献[5]给出。
1.2 动态映射函数1) 维也纳映射函数(Vienna mapping function1, VMF1)
维也纳理工大学的Boehm和Schuh采用数值天气模型计算映射函数,得到VMF模型[6],VMF和NMF模型具有相同的数学表达式。VMF模型经过一次改进,得到VMF1模型。VMF1模型的干、湿映射函数系数ah、aw可以近实时地从网站(http://mars.hg.tuwien.ac.at/~ecmwf1/)下载,bh=0.002 9, bw=0.001 46, cw=0.043 91, ch由下式计算:
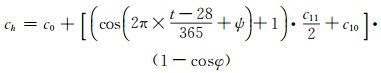
|
(5) |
式中,t为年积日,φ为纬度,参数c0、c10、c11、ψ可由索引表查取[6-7]。
2) 全球映射函数(global mapping function, GMF)
为解决VMF1模型中系数ah和aw求解过程中的时间延迟问题,Boehm等[8]提出了全球映射函数GMF模型,其形式与NMF模型相似。它是利用ECMWF(European center for medium-range weather forecasts)提供的40 a全球15°×15°分辨率的温度、压强和相对湿度的月平均廓线,采用射线追踪法[8-9]分析1999-09~2002-08的数据资料来确定系数ah、aw,而b、c仍采用VMF1模型计算值。GMF模型系数ah、aw按下式计算[8]:
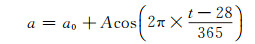
|
(6) |
式中,a0为平均值,A为年周期振幅,t为年积日。
2 评估GPS基线质量的两个指标 2.1 基线重复性基线重复性是衡量内符合精度的一个重要指标。基线重复性越小,内符合精度越高,基线质量就越好;反之,基线重复性越大,内符合精度越低,基线质量就越差。基线分量和边长的重复性定义为[10-11]:

|
(7) |
式中,n为同一基线总观测时段数, Li为一个单时段解的基线分量或边长, δi2是Li的方差, L为Li的加权平均值。
2.2 基线平均值的标准偏差平均值的标准偏差是相对于单次测量的标准偏差而言的。在一定的测量条件下,对同一未知量进行m组测量(每组皆测量n次),则对应每组的n次测量都有一个算术平均值,各组的算术平均值不一定相同,不过,它们的分散程度要比单次测量值的分散程度小得多。描述这m个平均值的分散程度,同样可以用标准偏差作为评定指标[12]。在GPS测量中,基线平均值L(最优估值)的标准偏差σ(L)可表示为:
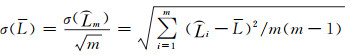
|
(8) |
式中,m为测量的组数, 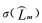
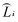
为了比较NMF、GMF和VMF1三种映射函数的基线处理效果,下文利用我国境内8个IGS站连续8 d、采样间隔为30 s的观测数据,应用GAMIT软件、最终精密星历、Saastamoinen天顶对流层延迟模型进行基线解算,通过改变映射函数模型和高度角来研究其对基线解算质量的影响。
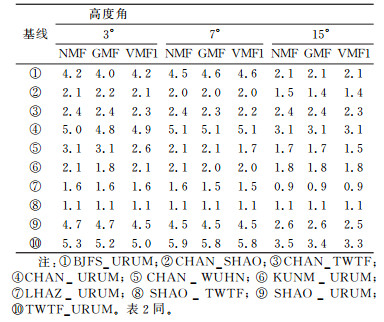
3.1 对基线重复性的影响NMF、GMF和VMF1三种模型解算的基线重复性见表 1(单位mm)。由表可见,不同模型在相同高度角时解算的同一基线重复性相差不大,基本都在0.3 mm以内,最大相差0.5 mm。在高度角为15°时,3种模型的基线重复性最大为3.5 mm,最小为0.9 mm;在高度角为7°和3°时,3种模型的基线重复性最大分别为5.9 mm和5.3 mm,最小为1.1 mm。3种模型的基线重复性均随卫星高度角的降低而增大,即基线精度随高度角降低而变差。当高度角从15°降到7°时,精度降低比较明显,但从7°降到3°时精度下降幅度变小。总体来看,动态映射函数GMF和VMF1的解算结果比NMF模型好,比较而言,VMF1又略优于GMF模型。
|
|
表 1 3种映射函数解算的基线重复性 Tab. 1 Baseline repeatability of three kinds of mapping functions/mm |
在GPS定位时,平面位置往往可以获得较高的精度,而在高程方向的误差较大。通过分解基线向量到N、E、U3个方向,计算不同方向的基线重复性,比较在低高度角时3种映射函数的解算精度。
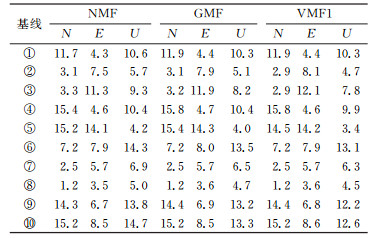
从表 2(单位mm)知,3种模型解算同一基线的N、E分量的重复性相差不大,大多在0.5 mm以内,最大相差0.8 mm;U分量差别则比较明显,同一基线的重复性相差大多在0.5 mm以上,最大相差2.1 mm。总的看来,动态映射函数GMF和VMF1的解算结果亦优于NMF模型,其中VMF1模型的解算结果又更好一些。可见在处理较低高度角数据时,应用动态映射函数能获得更好的高程精度,尤以VMF1模型为佳。
|
|
表 2 高度角3°时解算的基线分量的重复性 Tab. 2 Baseline component repeatability under elevation angle of 3° |
图 1是应用3种模型解算的不同长度基线的重复性。从图 1可知,3种模型解算的基线重复性均随基线长度的增加而增大,但GMF和VMF1模型的基线重复性总体比NMF模型小,说明动态映射函数解算的基线质量更好,其中又以VMF1模型的解算效果为佳。

|
图 1 基线重复性随长度的变化 Fig. 1 Baseline repeatability variation with its length |
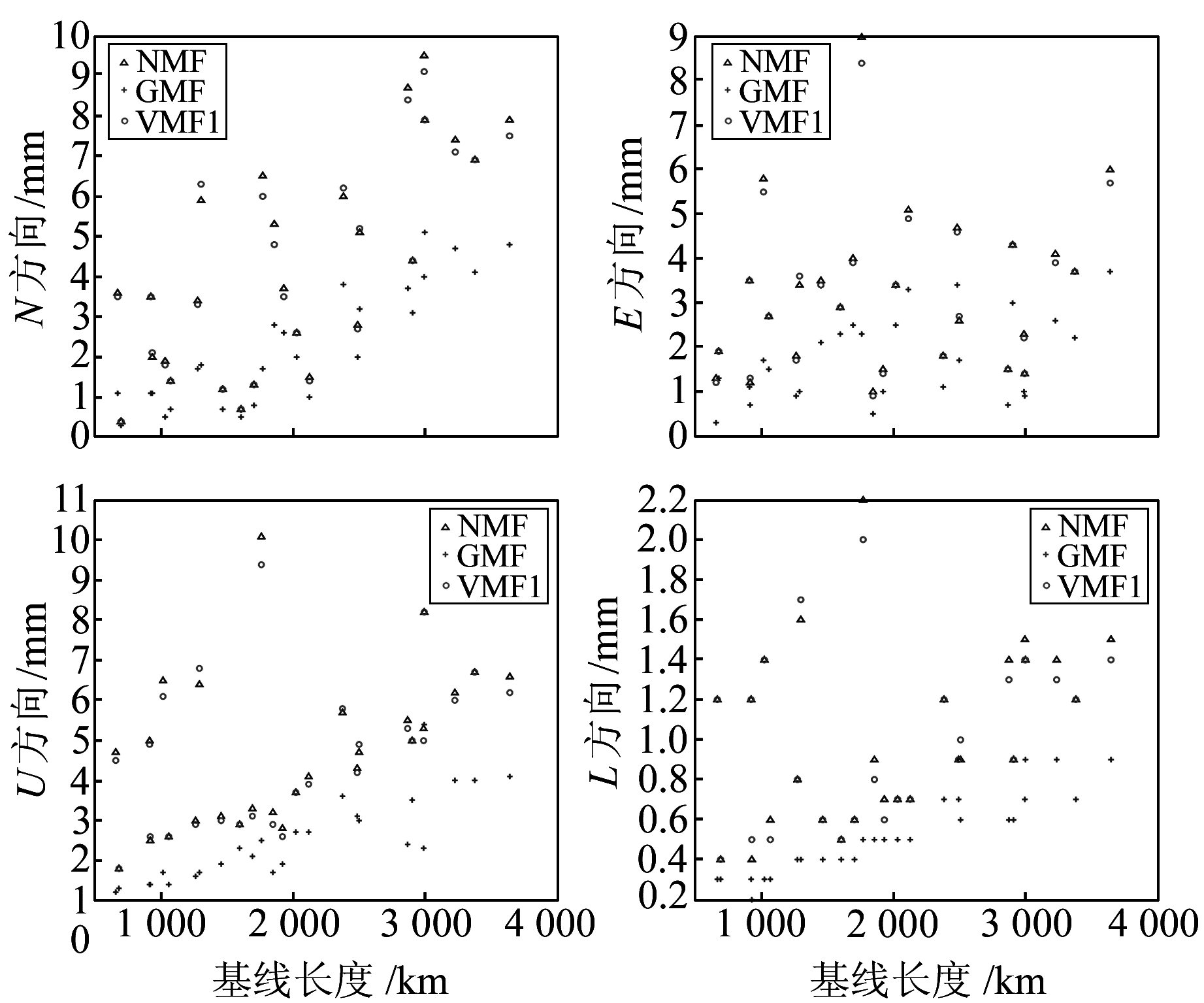
图 2是应用3种模型计算的基线不同方向平均值的标准偏差。由图可知,GMF模型解算的不同方向平均值的标准偏差都较小且集中,VMF1和NMF模型则比较分散,但VMF1模型也好于NMF模型。说明在基线解的集中性、稳定性、可靠性方面,动态映射函数GMF、VMF1的解算质量优于NMF模型,其中又以GMF模型的解算质量为最佳。分析原因认为,GMF模型利用了ECMWF提供的40 a的数据,数据量较大,而VMF1模型使用的是实时数据,随机变化比较大,因而VMF1的结果不如GMF,但也略优于NMF模型。
|
图 2 3种模型不同方向平均值的标准偏差 Fig. 2 Standard deviation of the mean value of three kinds of model in different directions |
由前述可知,3种模型解算的基线重复性均随卫星高度角的降低和基线长度的增加而增大、精度变差,动态映射函数GMF、VMF1总体比NMF模型要好,其中VMF1又略优于GMF模型。GMF模型解算的不同方向平均值的标准偏差都较小,质量最好;而VMF1和NMF模型分布比较分散,但VMF1模型又略好于NMF模型。总体上看,相对于NMF模型,动态映射函数GMF、VMF1的基线解算质量更好,其中VMF1模型在解算基线重复性时结果更好,而GMF模型在计算平均值的标准偏差时效果更佳。因此对于高精度基线处理,选用合适的动态映射函数能获得更好的结果。
| [1] |
姚宜斌, 曹娜, 许超钤, 等. GPT2模型的精度检验与分析[J]. 测绘学报, 2015, 44(7): 726-733 (Yao Yibin, Cao Na, Xu Chaoqian, et al. Accuracy Assessment and Analysis for GPT2[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(7): 726-733)
(  0) 0) |
| [2] |
Yao Y B, Xu C Q, Zhang B, et al. GTm-Ⅲ: A New Global Empirical Model for Mapping Zenith Wet Delays onto Precipitable Water Vapour[J]. Geophysical Journal, 2014, 197(1): 202-212 DOI:10.1093/gji/ggu008
(  0) 0) |
| [3] |
Yao Y B, Zhu S, Yue S Q. A Globally Applicable, Season-specific Model for Estimating the Weighted Mean Temperature of the Atmosphere[J]. Journal of Geodesy, 2012, 86(5): 1125-1135
(  0) 0) |
| [4] |
Yao Y B, He C Y, Zhang B, et al. A New Global Zenith Tropospheric Delay Model GZTD[J]. Chinese Journal of Geophysics, 2013, 56(7): 2218-2227
(  0) 0) |
| [5] |
Niell A. Global Mapping Functions for the Atmosphere Delay at Radio Wavelengths[J]. Journal of Geophysical Research: Solid Earth, 1996, 101(B2): 3227-3246 DOI:10.1029/95JB03048
(  0) 0) |
| [6] |
Boehm J, Schuh H. Vienna Mapping Functions in VLBI Analysis[J]. General Meeting Proceedings, 2004, 31(1): 277-281
(  0) 0) |
| [7] |
Boehm J, Cerveira P, Schuh H, et al. The Impact of Tropospheric Mapping Functions Based on Numerical Weather Models on the Determination of Geodetic Parameters[C]. IAG, Cairns, 2005
(  0) 0) |
| [8] |
Boehm J, Niell A, Tregoning P, et al. Global Mapping Function(GMF): A New Empirical Mapping Function Based on Numerical Weather Model Data[J]. Geophysical Research Letters, 2006, 33(7): 199-208
(  0) 0) |
| [9] |
郭际明, 章迪, 史俊波, 等. 利用射线追踪法分析3种典型对流层映射函数在中国区域的精度[J]. 武汉大学学报:信息科学版, 2015, 40(2): 182-187 (Guo Jiming, Zhang Di, Shi Junbo, et al. Using Ray-Tracing to Analyse the Precision of Three Classical Tropospheric Mapping Functions in China[J]. Geomatics and Information Science of Wuhan University, 2015, 40(2): 182-187)
(  0) 0) |
| [10] |
黄功文, 王斌, 王延伟. 高精度GPS控制网基线重复性检验与质量分析[J]. 测绘通报, 2011(7): 9-11 (Huang Gongwen, Wang Bin, Wang Yanwei. Baseline Repeatability Test and Quality Analysis of High-Precision GPS Control Network[J]. Bulletin of Surveying and Mapping, 2011(7): 9-11)
(  0) 0) |
| [11] |
李建虎, 张胜凯, 鄂栋臣, 等. 南极中山站数据处理中IGS框架站的选择[J]. 大地测量与地球动力学, 2010, 30(2): 61-65 (Li Jianhu, Zhang Shengkai, E Dongchen, et al. On Selection of Framework Stations' for Data Processing of Antarctic Zhongshan Station[J]. Journal of Geodesy and Geodynamics, 2010, 30(2): 61-65)
(  0) 0) |
| [12] |
李启华, 余锦, 刘菊英. 标准偏差和平均值的标准偏差探讨[J]. 金属材料与冶金工程, 2013, 41(5): 45-48 (Li Qihua, Yu Jin, Liu Juying. Discussion on Standard Deviation and Standard Deviation of the Mean Value[J]. Metal Materials and Metallurgy Engineering, 2013, 41(5): 45-48 DOI:10.3969/j.issn.1005-6084.2013.05.011)
(  0) 0) |
2. Guangxi Key Laboratory of Spatial Information and Geomatics, 319 Yanshan Street, Guilin 541006, China;
3. Hydrography Department Shanghai Maritime Safety Administration, Donghai Navigation Safety Administration, 7 Lane 82, Gongqing Road, Shanghai 200086, China
 2017, Vol. 37
2017, Vol. 37