地球的运动非常复杂,其变化是由地外天体引力、地表及内部物质迁移和固体地球负载形变共同作用的结果。地球自转参数(earth rotation parameters, ERP)是描述地球运动状态的主要参数,它的变化反映了上述几种作用对地球自转的影响。地球自转参数主要包括两个部分:极移和日长变化。高精度的地球自转参数是提高空间导航定位技术精度的基础数据,对建立天球参考框架和地球参考框架具有重要意义[1]。另外,高精度ERP参数也是地球海洋大气系统的敏感器[2],在飞行器精密定轨和自主导航、大地控制网的建立和深空探测等方面都发挥着重要的作用[3]。
目前确定地球自转参数的主要技术手段有:甚长基线干涉测量(very long baseline interferometry, VLBI)、卫星激光测距(satellite laser ranging, SLR)、全球卫星导航定位系统(global navigation satellite system, GNSS)、卫星多普勒雷达和无线电定位系统(doppler orbitography and radiopositioning integrated by satellite, DORIS)等[4]。相比其他技术,GPS数据量充足,设备价格低廉,操作简单,且能够获得高分辨率和长时间跨度的地球自转参数。
然而,由于计算机硬件条件的限制,利用全球GPS数据解算ERP参数的时间会随着测站数的增多、观测弧段的增加呈几何级数增加,给ERP的解算带来非常大的困难。因此,在利用GPS数据解算ERP参数的过程中,测站数目的选择和观测弧段的选取是非常重要的两个因素。文献[5-6]中曾对这个问题有过一些探讨,但是,近些年鲜有学者系统地研究测站数目和观测弧段对ERP参数最终解算精度的影响。鉴于上述原因,本文研究测站数目和观测弧段对ERP参数最终解算精度的影响。
1 GPS解算ERP的原理由于接收机的坐标一般都是在国际地球参考系统(international terrestrial reference frame, ITRF)中给出的,而通常会把卫星及接收机的位置矢量换算到同一天球参考系统(international celestial reference frame, ICRF)中来计算星间距离ρ。所以需要将接收机ITRF的坐标转换到ICRF中,它们的转换关系为R(ti)=PNSWRoi,其中P、N为岁差、章动旋转矩阵;S为地球自转矩阵;W为极移矩阵。
本文采用双差模型来解算ERP参数,待估参数为测站坐标、卫星坐标、ERP参数和中性大气延迟。将GPS载波相位观测值表示为待估计的函数模型为[7-8]:
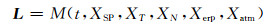
|
(1) |
式中,M表示观测量与参数的函数模型;t为时间;XSP为初始时刻的轨道根数和摄动参数(辐射压模型);XT为测站坐标;XN为相位模糊度;Xerp为地球自转参数,包括极移参数xP、yP和日长变化参数DR;Xatm为大气延迟。对式(1)线性化:

|
(2) |
式中,C0表示由近似参数计算出来的理论观测值,ε为观测噪声[9-10]。
转换矩阵在极移x和y方向上的分量为:
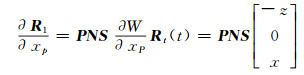
|
(3) |
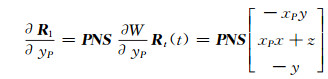
|
(4) |
式中,R1为测站在惯性坐标系统中的位置矢量,xP和yP为极移在x、y方向的分量,DR为UT1-UTC的一阶变化率,即日长变化,则:
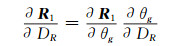
|
(5) |

|
(6) |
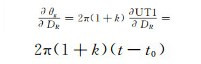
|
(7) |
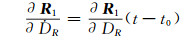
|
(8) |
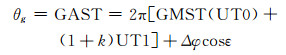
|
(9) |
式中,GAST(Greenwich apparent sidereal time)为格林尼治恒星时,GMST(Greenwich mean sidereal time)为格林尼治平恒星时,Δφ为黄经章动,ε为黄赤交角,站坐标与卫星轨道参数来自IGS站[11-12]。通过以上解算,可求出地球自转参数。
2 数据处理与分析 2.1 测站数目对ERP解算精度的影响在探究测站数目对解算ERP参数的影响时,首先应当保证有足够的观测弧段。本文在保持观测弧段不变的情况下,利用全天24 h的GPS数据进行解算。在解算的过程中,依次将IGS测站数目从10增加到90,递增间隔为10。表 1给出了解算过程中依次递增的测站名称。另外,在选取IGS测站时,主要考虑以下几个因素:一是尽可能多地选取ITRF2008框架下的GPS观测站,测站坐标中误差在1 mm以下,并且速度场中误差小于0.3 mm/a;二是所选取的测站应当尽量均匀分布[13-14]。
|
|
表 1 解算时递增的测站名称 Tab. 1 The name of increasing stations |
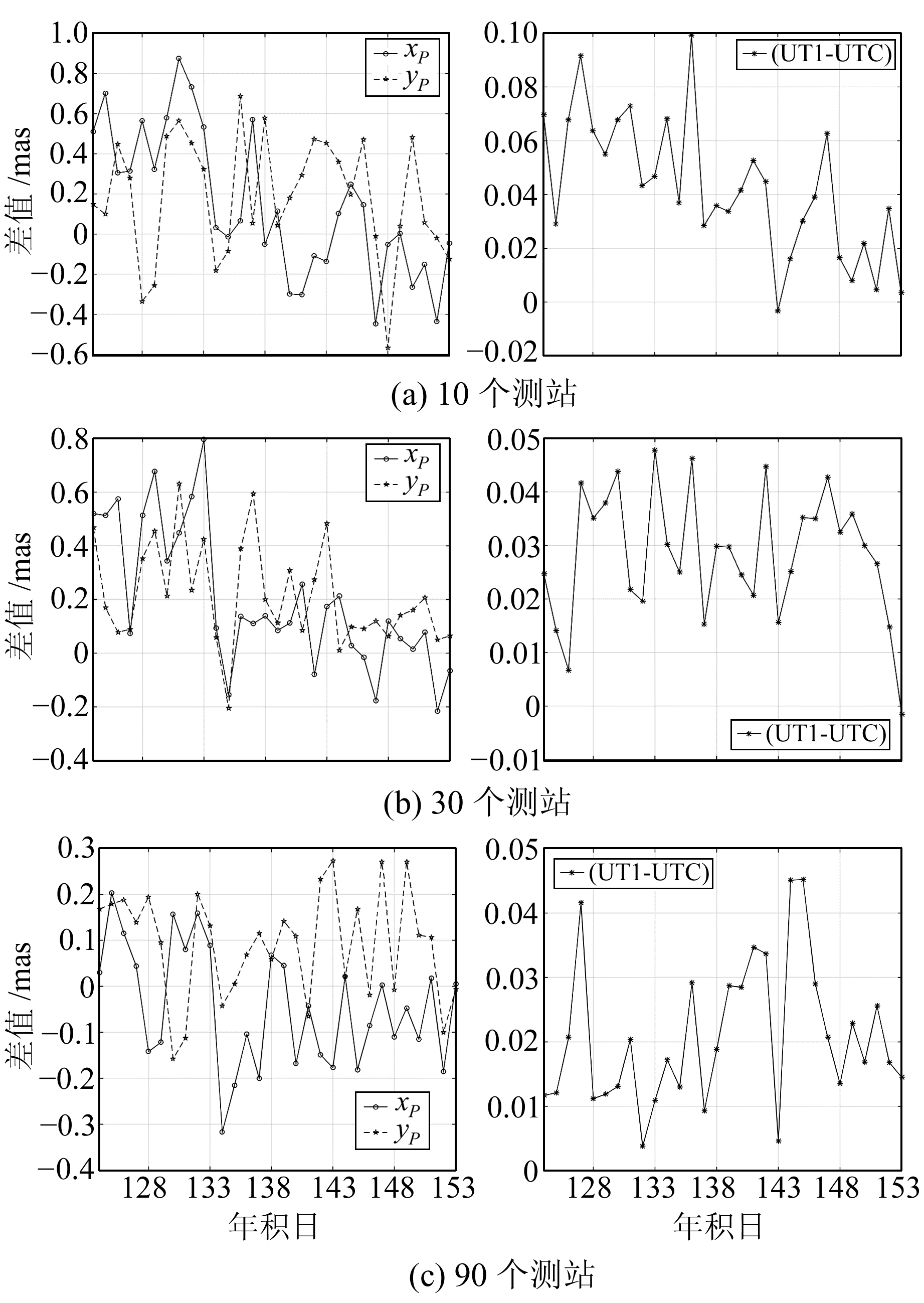
本文采用2015-05-04~06-02共30 d的数据(个别参考站可能没有当天的数据,此时采用其周围的参考站数据来代替)并采用bernese软件进行数据处理。利用每天24 h观测弧段的数据依次解算测站数目分别为10、20、30、…、90时所对应的地球自转参数。解算完成后,剔除个别异常值,并将其与IGS发布的ERP时间序列(UTC 12:00)进行比较。测站数目为10、30和90时,其xP、yP和UT1-UTC的差值如图 1所示。
|
图 1 不同测站数目时GPS解算结果与IGS发布ERP之差 Fig. 1 The difference of ERP between the results of GPS solution and IGS with different number of station |
从图 2可以看出,随着测站数目的增加,解算出的极移xP、yP和UT1-UTC的精度逐渐提高,尤其是当测站数从10增加到40时,精度提高显著。当测站数增加到40之后,极移xP、yP的解算精度提高不再明显,逐渐趋于平稳,即使当测站数增加到90时,精度也不再有明显的变化,但计算时间却成倍的增加。UT1-UTC的解算精度变化情况和xP、yP类似,在测站数增加到40以后一直趋于平缓。基于此,笔者建议在衡量解算精度和消耗时间之间,应该理性选择相应的测站数目,来解算ERP参数。

|
图 2 测站数目与ERP计算精度的关系 Fig. 2 The relationship between the number of station and the precision of ERP |
|
|
表 2 不同测站数目30 d ERP均方根值 Tab. 2 The RMS values of ERP for 30 days with different number of station |
另外,本次实验中每次增加的10个IGS测站要均匀分布于全球各地,这样有助于提高ERP的计算精度。在数据解算的过程中,测站选取有多种情况,测站均匀分布情况不同,就会导致整个GPS网的空间结构不同。大量的实验数据表明,虽然每次所选取的测站均匀分布情况不同,但是相同测站数目且整体均匀分布在全球各地时,解算出的ERP参数精度会有一些微小差异,整体浮动不会太大,基本符合上述实验所得出的结论。
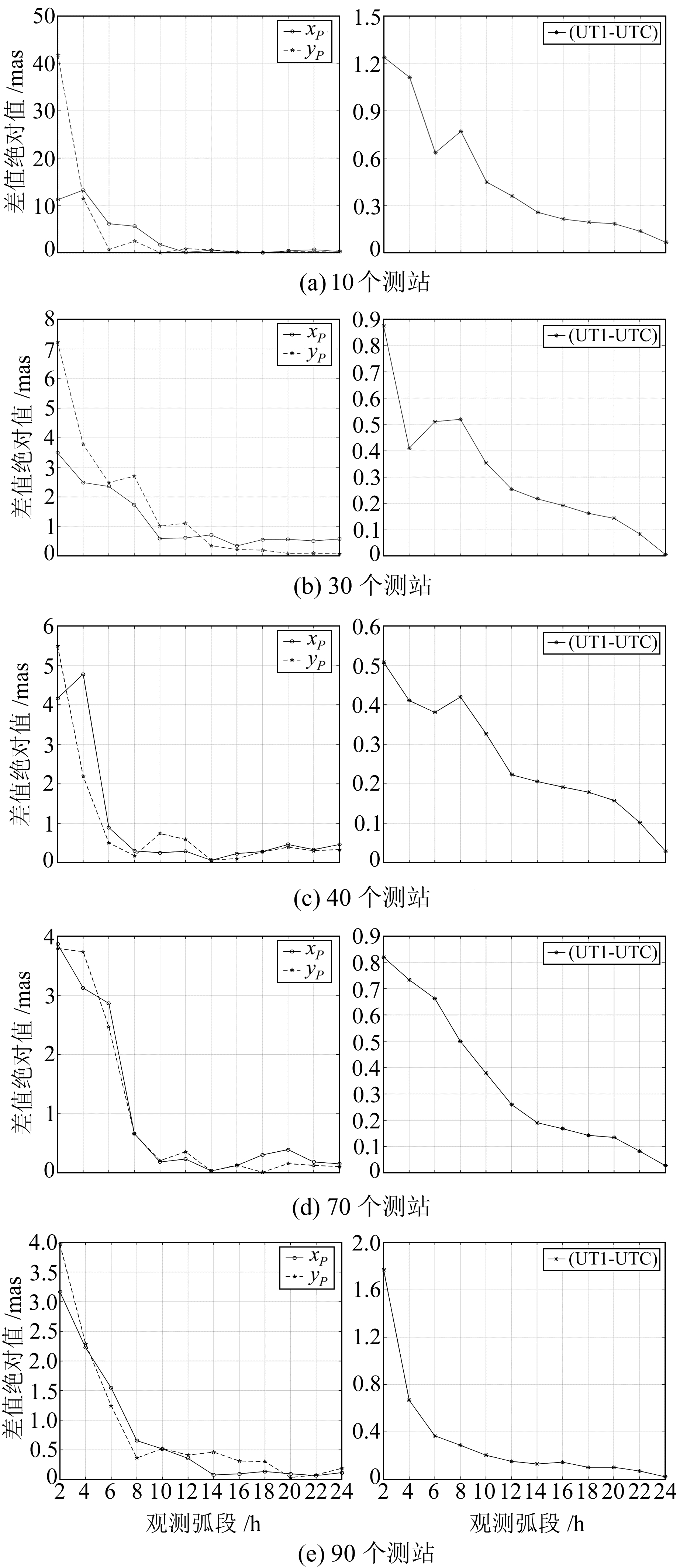
2.2 观测弧段长度对ERP解算精度的影响在探究观测弧段对ERP解算精度的影响时,我们保持所选用的测站数不变,利用不同观测弧段长度的数据解算ERP参数,观测弧段长度从2 h开始,按2 h递增直到24 h。限于篇幅,本文只选择测站数为10、30、40、70、90时5幅有代表性的图来反映不同测站数目时观测弧段对ERP解算精度的影响情况(图 3)。
|
图 3 不同测站数目时ERP解算精度与观测弧段的关系 Fig. 3 The relationship between the precision of ERP and observation arcs with different number of stations |
从图 3可以看出,极移xP、yP在观测弧段从2 h增加到10 h的过程中精度提高非常显著,波动明显;在观测弧段从10 h到24 h的过程中,精度提高不是十分明显,尤其是当观测弧段到达14 h之后,其精度基本趋于稳定。UT1-UTC精度变化情况稍有不同,在观测弧段从2 h到8 h的过程中,其解算精度上下浮动,不太稳定,但是浮动幅度不是很大。当解算弧段增加到8 h以后,其解算精度稳步提升,且随着观测弧段的增加一直在提高。
上述精度变化情况是从整体上所得出的结论。当固定不同的测站数目、改变观测弧段长度时,其中的趋势也略有差异,但是整体情况基本相同。因此,在解算ERP参数时,可以根据上述图幅所显示的信息,在选择不同的测站数目时,自主地选择解算的弧段长度,以达到最佳解算效率和最佳解算精度的目的。
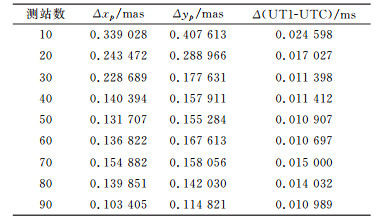
3 结语本文详细研究了利用全球IGS测站解算ERP参数时测站数目和观测弧段对最终ERP解算精度的影响。大量的实验数据表明,当观测弧段保持不变时,一般可以选择40个在全球均匀分布的IGS站,解算的精度与IGS所发布的ERP参数比较,极移在x方向差值的RMS为0.140 4 mas,极移在y方向差值的RMS为0.157 9 mas,UT1-UTC差值的RMS为0.011 4 ms。其差别均在IERS C04的精度范围之内[15],这说明本文的解算结果是可信的。当解算的测站数保持不变时,可以根据不同的精度需求选择不同的解算弧段长度,一般解算弧段长度应在10 h以上。如何选择测站使GPS网形最优化以及提高多系统解算ERP参数的效率将是下一步研究工作的重点。
| [1] |
Wei E H, Yan W, Jin S G, et al. Improvement of Earth Orientation Parameters Estimate with Chang'E-1 ΔVLBI Observations[J]. Journal of Geodynamics, 2013, 72: 46-52 DOI:10.1016/j.jog.2013.04.001
(  0) 0) |
| [2] |
Wei E H, Jin S G, Zhang Q, et al. Autonomous Navigation of Mars Probe Using X-Ray Pulsars: Modeling and Results[J]. Advances in Space Research, 2013, 51(5): 849-857 DOI:10.1016/j.asr.2012.10.009
(  0) 0) |
| [3] |
Koenig D, Koenig R, Neumayer K, et al. Station Coordinates, Low Degree Harmonics, and Earth Rotation Parameters from an Integrated GPS/CHAMP/GRACE Processing[J]. Journal of Non-Equilibrium Thermodynamics, 2007, 3(4): 197-212
(  0) 0) |
| [4] |
魏二虎, 万丽华, 金双根, 等. 联合GNSS和SLR观测对地球自转参数的解算与分析[J]. 武汉大学学报:信息科学版, 2014, 39(5): 581-585 (Wei Erhu, Wan Lihua, Jin Shuanggen, et al. Estimation of ERP with Combined Observations of GNSS and SLR[J]. Geomatics & Information Science of Wuhan University, 2014, 39(5): 581-585)
(  0) 0) |
| [5] |
朱圣源, 赵铭. 多种技术测定地球自转参数综合解的简化算法[J]. 中国科学院上海天文台年刊, 1986, 50-55 (Zhu Shengyuan, Zhao Ming. A Simplified Algorithm for the Joint Solution of Multi-Techniques of ERP[J]. Annals of Shanghai Observatory Academia Sinica, 1986, 50-55)
(  0) 0) |
| [6] |
魏二虎, 李广文, 畅柳, 等. 利用GPS观测数据研究高频地球自转参数[J]. 武汉大学学报:信息科学版, 2013, 38(7): 818-821 (Wei Eerhu, Li Guangwen, Chang Liu, et al. On the High-Frequency ERPs with GPS Observations[J]. Geomatics and Information Science of Wuhan University, 2013, 38(7): 818-821)
(  0) 0) |
| [7] |
何战科, 杨旭海, 李志刚, 等. 利用GPS观测资料解算地球自转参数[J]. 时间频率学报, 2010, 33(1): 69-76 (He Zhanke, Yang Xuhai, Li Zhigang, et al. Estimation of Earth Rotation Parameters Based on GPS Observations[J]. Journal of Time & Frequency, 2010, 33(1): 69-76 DOI:10.3969/j.issn.1674-0637.2010.01.012)
(  0) 0) |
| [8] |
徐天河, 张丽萍, 李敏, 等. 利用全球IGS站GPS数据确定地球自转参数[J]. 测绘科学与工程, 2013(3): 8-13 (Xu Tianhe, Zhang Liping, Li Min, et al. Earth Rotation Parameters Determination Based on Daily GPS Data of Global IGS Stations[J]. Geomatics Science and Engineering, 2013(3): 8-13)
(  0) 0) |
| [9] |
Kouba J. Testing of the IERS2000 Sub-Daily Earth Rotation Parameter Model[J]. Studia Geophysica et Geodaetica, 2003, 47(4): 725-739 DOI:10.1023/A:1026338601516
(  0) 0) |
| [10] |
Meindl M, Dach R, Thaller D, et al. The Impact of the Processing Batch Length in GNSS Data Analysis on the Estimates of Earth Rotation Parameters with Daily and Sub-Daily Time Resolution[C]. EGU General Assembly, 2012
(  0) 0) |
| [11] |
周忠谟. GPS卫星测量原理与应用[M]. 北京: 测绘出版社, 1992 (Zhou Zhongmo. Principle and Application of GPS Satellite Measurement[M]. Beijing: Surveying and Mapping Publishing House, 1992)
(  0) 0) |
| [12] |
Sošnica K, Thaller D, Dach R, et al. Impactof Loading Displacements on SLR-Derived Parameters and on the Consistency between GNSS and SLR Results[J]. Monthly Notices of the Royal Astronomical Society, 2013, 87(8): 751-769
(  0) 0) |
| [13] |
Tercjak M, Boehm J, Brzezinski A. On the Possibility of Estimation of the Diurnal and Sub Diurnal Components of Earth Rotation from GNSS Data Analysis by Applying the Complex Demodulation[C].EGU General Assembly, 2014
(  0) 0) |
| [14] |
Yao Y B. Earth Rotation Parameter Estimation by GPS Observations[J]. Geo-Spatial Information Science, 2006, 9(4): 260-264 DOI:10.1007/BF02826737
(  0) 0) |
 2017, Vol. 37
2017, Vol. 37