2. 云南省地震局,昆明市北辰大道148号, 650225;
3. 防灾科技学院地震科学系,北京市学院大街465号, 101601;
4. 中国地震局地球物理研究所,北京市民族大学南路5号, 100081
在一些中强震前后,震源区构造应力场在时间和空间上都存在着某些变化特征[1-2]。Ickrath等[2]采用加入阻尼的滑动方向拟合法,利用震源机制解数据分时段进行应力张量反演后发现,在1999年伊兹米特MW7.4地震后2个月的余震期间,构造应力场有着明显的时空变化,应力类型由最初的走滑型变为EW向的正断型,随着余震的快速衰减,应力场最终又恢复到了初始状态。然而,大地震发生后,余震震源机制解数据往往比较复杂、紊乱。学者们大多通过空间分区的方式来反演分析震源机制解数据比较复杂情况下的构造应力场的空间分布特征,即将研究区分成若干小区,对每个小区的震源机制解数据进行构造应力张量的拟合反演。但分区方式的不同和分区大小的变化都可能对反演的应力张量结果产生影响[3]。因此,在中强震后构造应力场不断调整变化的情况下,如何尽可能减少人为分区因素,利用复杂紊乱的余震震源机制解,比较科学、细致地反演分析震源区构造应力场特征就成为学者们关心的问题。
本文基于1994年美国北岭MW6.7地震的62次MW≥3.0余震震源机制解,利用Michael[4-5]提出的构造应力张量反演方法,采用尽可能减少人为分区因素的思路,对北岭震源区的构造应力状态进行反演分析,并结合余震震源机制解分布和深部构造特征,探讨了北岭地震后震源区应力状态的调整变化及其与地质构造的关系。
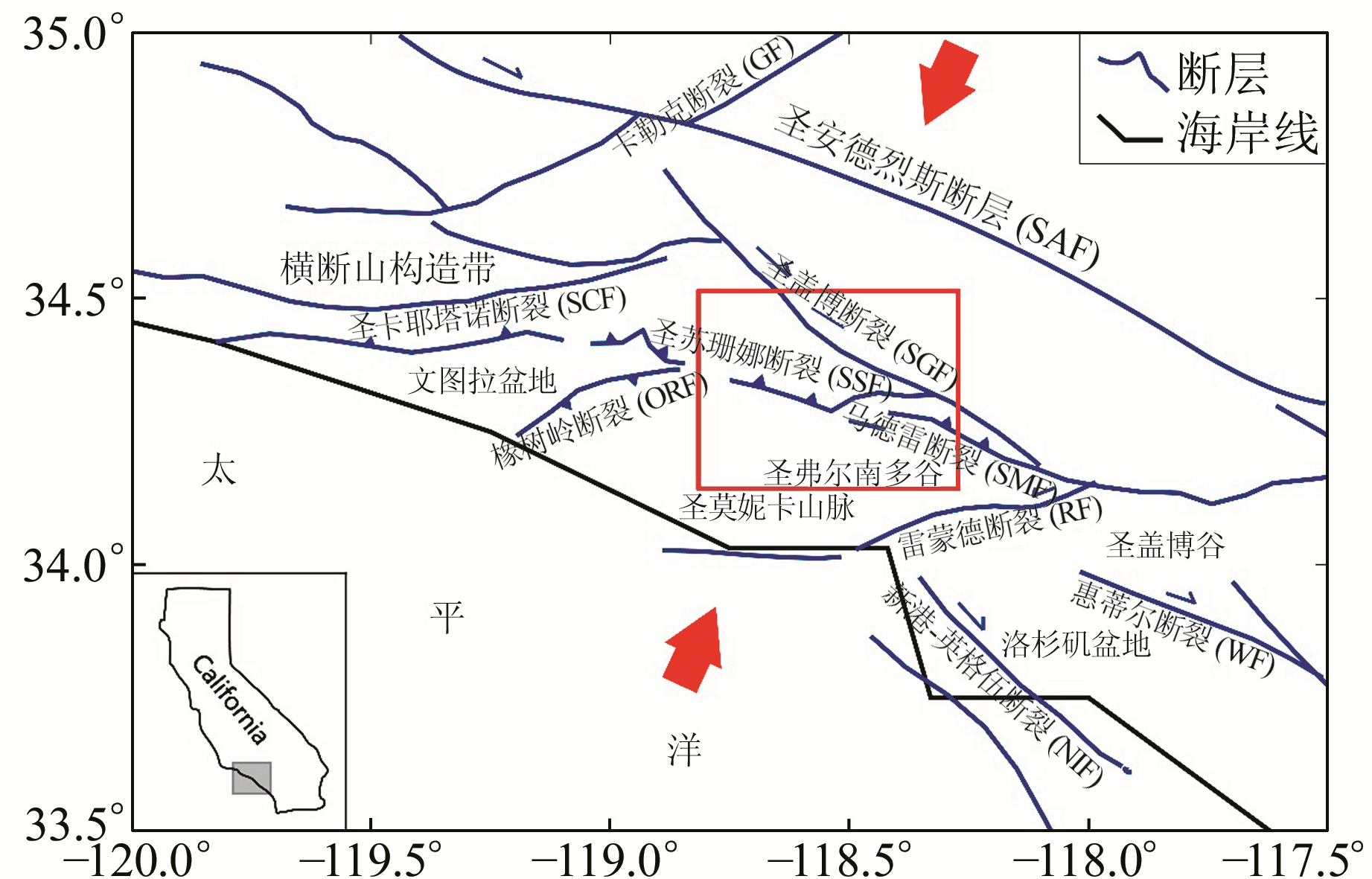
1 北岭地震的构造背景及余震震源机制解1994-01-17美国洛杉矶圣弗尔南多谷的北岭地区发生MW6.7地震,震中位置为34.21°N、118.55°W,震源深度大约为18 km。北岭地区邻近的大型区域构造主要有北西向的圣安德烈斯断裂带、近东西向的横断山构造带、圣弗尔南多盆地和洛杉矶盆地(见图 1,图中红色方框区域为北岭震源区,红色箭头为区域应力场最大主应力方位)。该地区构造较为复杂,区内分布着一系列北西走向的断裂(图 2),浅部的断裂一般倾角较大,接近直立,如圣盖博断裂和圣苏珊娜断裂等[6]。而圣弗尔南多断裂则切割较深,并且倾角较小,约为30°,倾向为北东[7]。前人通过对北岭地震余震的研究认为,发生地震的北岭断裂大致从地下18 km延伸至距地表 5~8 km处,没有破裂到地表,断层倾向为西南向,倾角为40°左右[7]。
|
图 1 南加州地区地质构造简图 Fig. 1 The sketch showing geological tectonics of southern California |
|
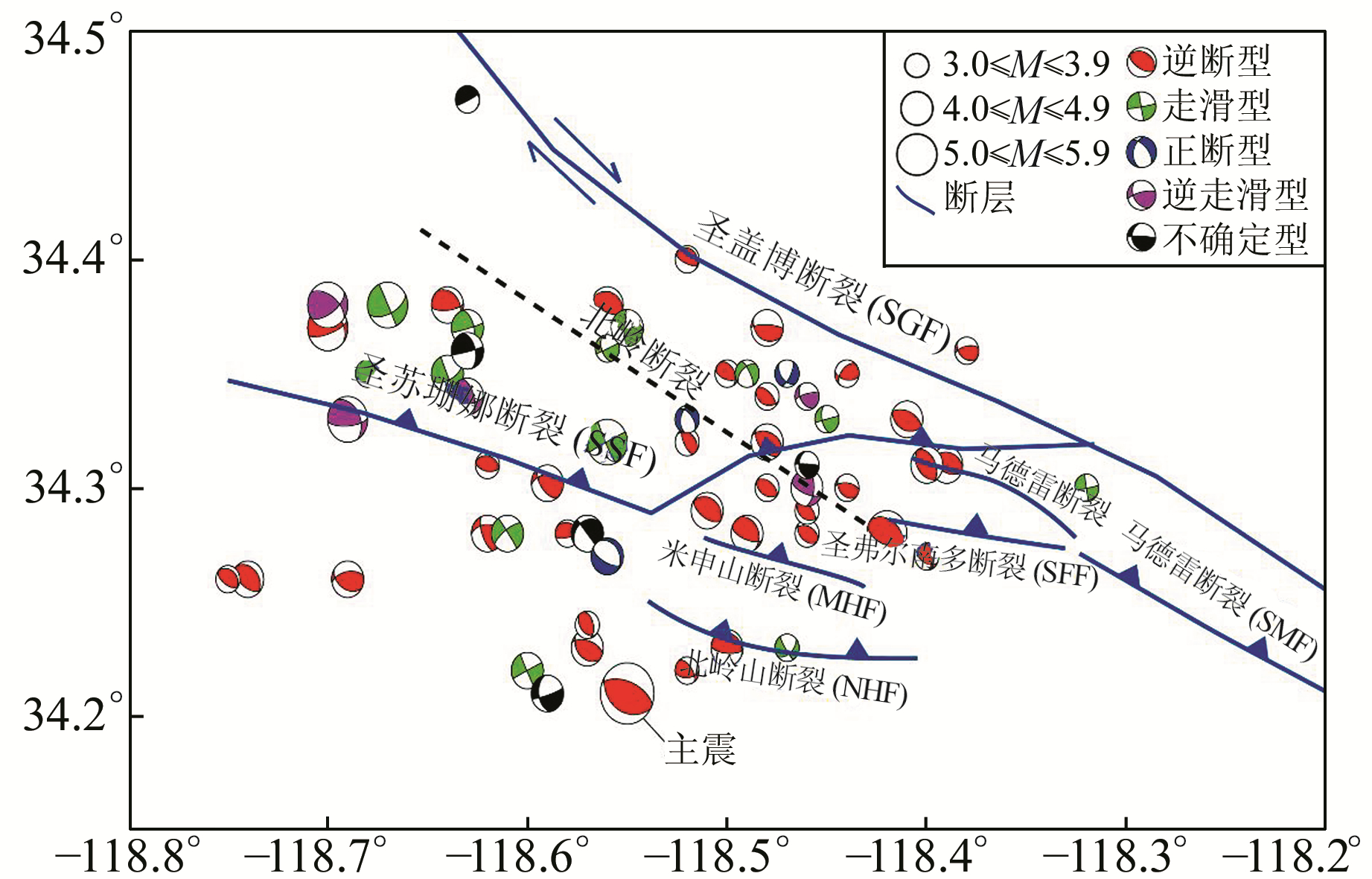
图 2 北岭余震震源机制解和主要构造分布示意图 Fig. 2 The distribution of Northridge aftershock mechanisms and main structures |
北岭主震的震源机制解为逆断型,Thio等[8]利用短周期面波反演计算了1994-01~08期间的62次MW≥3.0余震的震源机制解(图 2)。这些余震震源机制解比较复杂,按照世界应力图[9]的划分原则,62个余震震源机制解中,逆走滑型和逆断型震源机制解共有39个,占62.9%;走滑型地震有15个,占24.2%;正断型震源机制解共有3个,占4.8%;不确定型震源机制解共5个,占8.1%。对这些震源机制解进行深入分析,不仅能够进一步明晰北岭震源区构造应力状态,同时对深入了解北岭地震孕育发生的力学环境、分析地震活动与构造应力之间的关系具有重要意义。
2 研究方法和思路利用大量震源机制解数据反演平均构造应力张量方法(也称滑动方向拟合法[1]),能够较好地避免由单个数据刻画地壳应力的偏差。基于滑动方向拟合法的思想,不同学者给出了不同的应力张量反演算法。其中,Michael[4-5]按照剪应力方向与断层滑动方向相一致的原则,提出了将非线性问题转化为线性反演应力张量的算法,提高了反演应力张量的计算效率。Wiemer等[10]将Michael算法集成到可视化的ZMAP软件包中,其应力张量反演有2个计算模块,一是最优应力张量反演模块,该模块依据输入的震源机制解数据,反演给出输入震源机制解约束下的最优应力张量反演结果,包括应力张量中的3个主应力方向及其置信区间、反映3个主应力相对大小的应力形因子φ以及β值(其定义为断层面上剪应力方向和滑动方向之间夹角的平均值,简称为平均剪滑角);二是区域分网格反演模块,该模块首先对研究区域进行网格划分,选取每个网格节点周围的若干个震源机制解进行反演计算,根据各个网格节点的应力张量计算结果,给出最大主应力方向的平面分布图和应力张量方差平面分布图。
ZMAP软件包给出了3个参数用来表征参与计算的震源机制解对反演结果的约束程度和反演结果的可靠性。在最优应力张量反演模块中,如果3个主应力方向的置信区间和平均剪滑角越大,表明参与计算的震源机制解对反演结果的约束就越差,反演结果的可靠性就越低。在区域分网格反演模块中,如果网格节点上的应力张量方差较大,则表明该网格节点周围的震源机制解比较紊乱,对反演结果的约束不好,反演结果的可靠性不高。Lu等[11]用应力张量方差来表征反演得到的构造应力场的均匀程度,认为应力张量方差大于0.2时,区域的构造应力场是非均匀的,当方差小于0.1时,意味着可以用1个统一的应力张量来解释观测到的震源机制解,说明该研究区域的应力场是均匀的。
由于北岭地震的余震震源机制解(图 2)比较复杂,为了能够在尽量减少人为分区因素的情况下,尽可能科学合理地展现北岭地震后震源区构造应力状态的分布特征,本文借助ZMAP软件包的特点,采用如下思路对震源区构造应力状态进行反演分析:首先进行初步反演计算,使用ZMAP软件包中的最优应力张量反演模块和区域分网格反演模块,对62个余震震源机制解进行反演计算,根据反演结果给出的3个参数(3个主应力方向的置信区间、平均剪滑角和应力张量方差)来观察反演结果的可靠性,如果3个主应力方向的置信区间和平均剪滑角比较大,反演结果的可靠性较差,则观察区域分网格反演模块给出的应力张量方差的分布情况,应力张量方差大的地方必然存在着与周围差异比较大的震源机制解(称为异常数据),尝试将其找出;然后进行分组计算,按照异常数据的空间分布和震源区主要断裂的展布特征,对62次余震震源机制解进行分组,运用ZMAP软件包对分组数据进行反演计算,依据反演结果,分析北岭地震后震源区构造应力状态特征。
3 反演计算 3.1 初步反演计算按照上节的分析思路,首先使用最优应力张量反演模块对北岭地震的62个余震震源机制解(不含主震)进行反演,计算结果见表 1,3个主应力方向及其95%的置信区间见图 3(图中彩色区域为各主应力轴方位95%的置信区间)。可以看出,最优应力张量的最大主应力为近水平,方向为北北东向,应力类型为逆断型。其中最大主应力轴的置信区间较小,而中间主应力轴和最小主应力轴的置信区间很大,表明反演结果对最大主应力轴的方位和倾角约束较好,对中间主应力轴和最小主应力轴的方位约束也比较好,但中间主应力轴和最小主应力轴的倾角约束很差。另外,平均剪滑角β为29.4°,也明显偏大。
|
|
表 1 最优应力张量反演结果 Tab. 1 The results of the best fitting stress tensor inversion |

|
图 3 主应力轴及其置信区间的下半球等面积投影 Fig. 3 Lower-hemisphere equal-area projections of principle stress axes and their confidence regions |
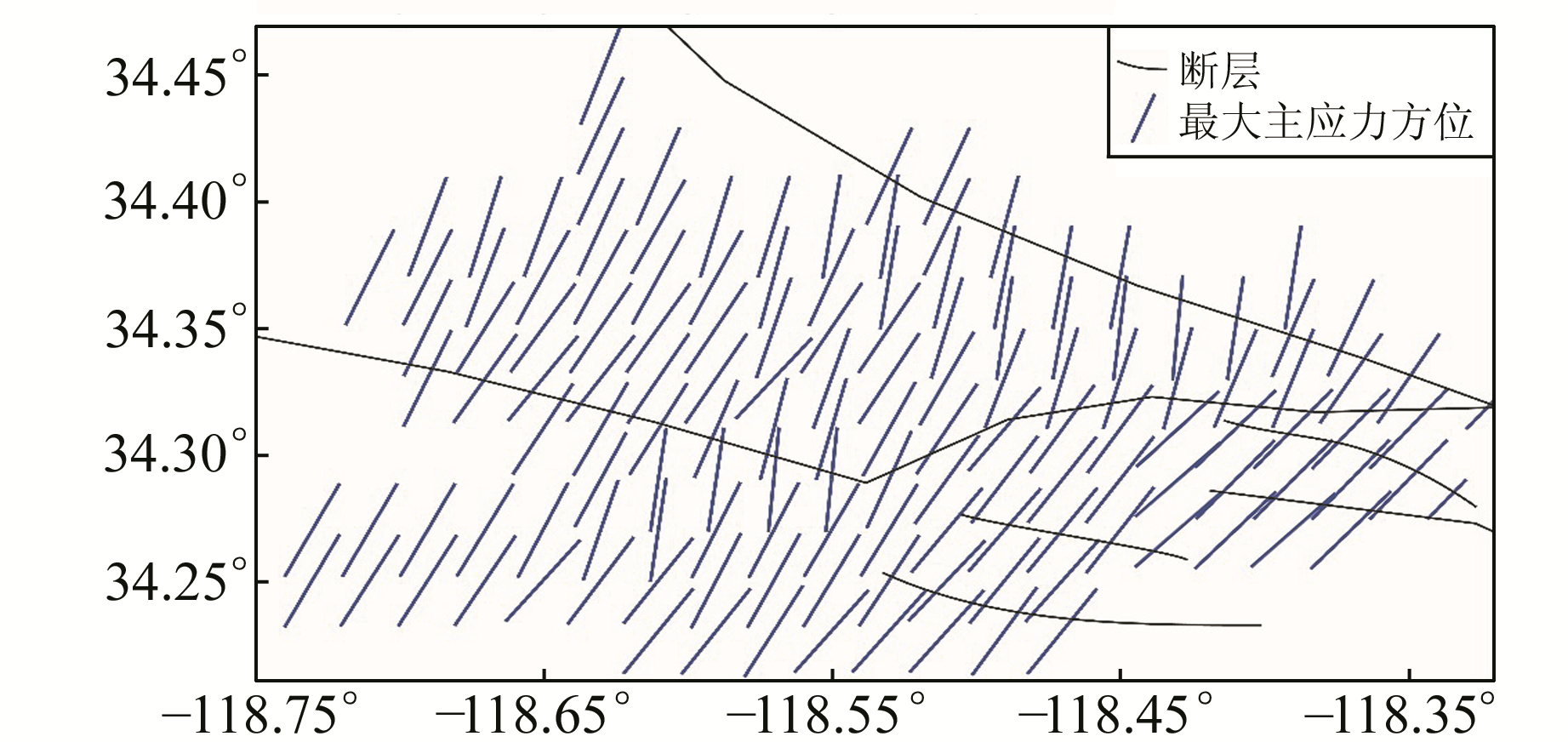
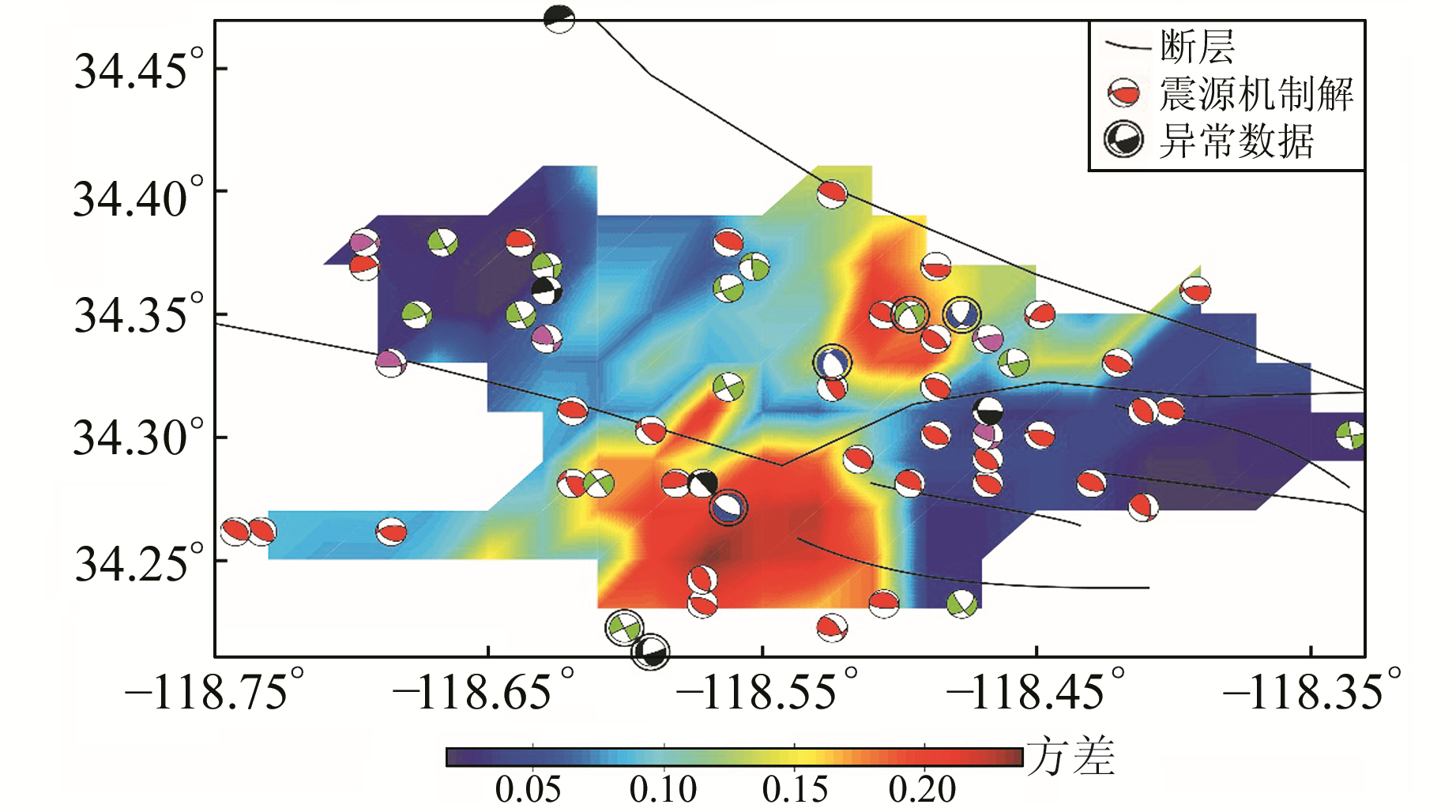
为了进一步考察反演结果的可靠性,对北岭震源区以0.02°×0.02°间距进行网格划分,利用区域分网格反演模块进行反演计算,计算时选取网格节点周围震源机制解个数最少为8个。图 4为区域分网格反演模块得到的震源区最大主应力轴方位分布图。可以看出,总体上整个震源区最大主应力方向较为一致,以北北东向为主,与上述最优应力张量反演模块给出的最大主应力方向相吻合(图 3),只是在震源区中部出现了少数最大主应力方向为近南北向的情况。图 5为区域分网格反演模块得到的震源区应力张量方差分布图,图中震源机制解符号含义同图 2,圆圈标注的为异常数据。可以看出,应力张量方差的分布很不均匀,震源区中部地区的应力张量方差较大,而东西两侧相对较小,特别是中部南侧呈现出较高的应力张量方差,普遍大于0.2。
|
图 4 北岭震源区最大主应力方位分布图 Fig. 4 The distribution of maximum principal stress orientation in source region |
|
图 5 北岭震源区应力张量方差分布图 Fig. 5 The distribution of stress tensor variance in source region |
综合上述计算结果认为,初步反演计算结果给出的最大主应力方向还是比较可靠的。但是对于中间主应力和最小主应力,其95%的置信区间很大,说明利用62个余震震源机制解进行整体反演所得结果的可靠性并不是很好,同时,区域分网格反演模块给出的应力张量方差的分布也不均匀。为此,开展下一步反演分析工作。
3.2 分组反演分析以往的研究在运用Michael算法来反演构造应力张量时发现,在应力张量方差值高的区域,其主应力方向的置信区间比应力张量方差值低的范围大,反演得到的主应力方位和应力类型的可靠性较差。在前人的研究中,一般只用应力张量方差来表征反演得到的构造应力场的均匀程度[11],很少有根据应力张量方差的分布来开展进一步的研究分析。
1) 剔除异常数据组
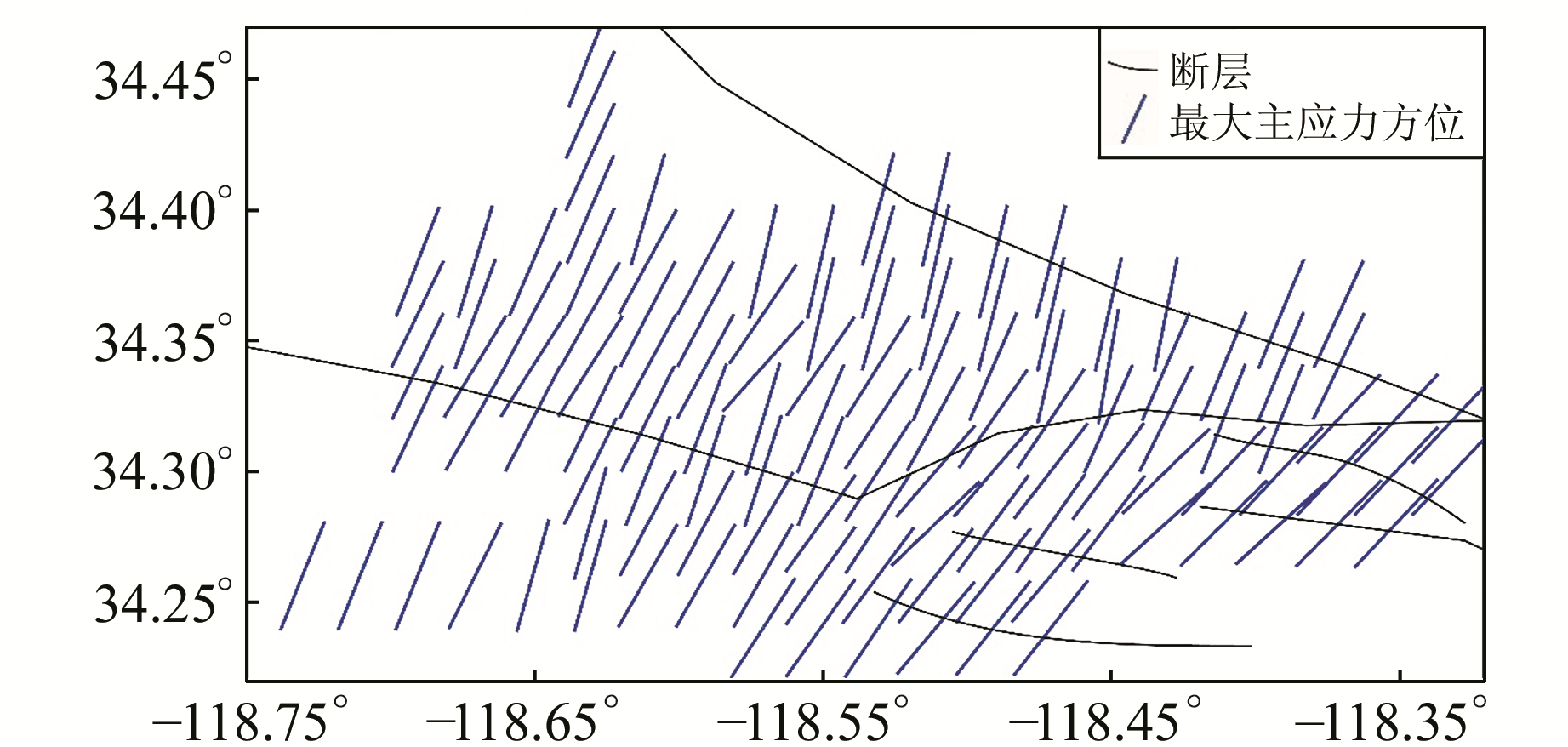
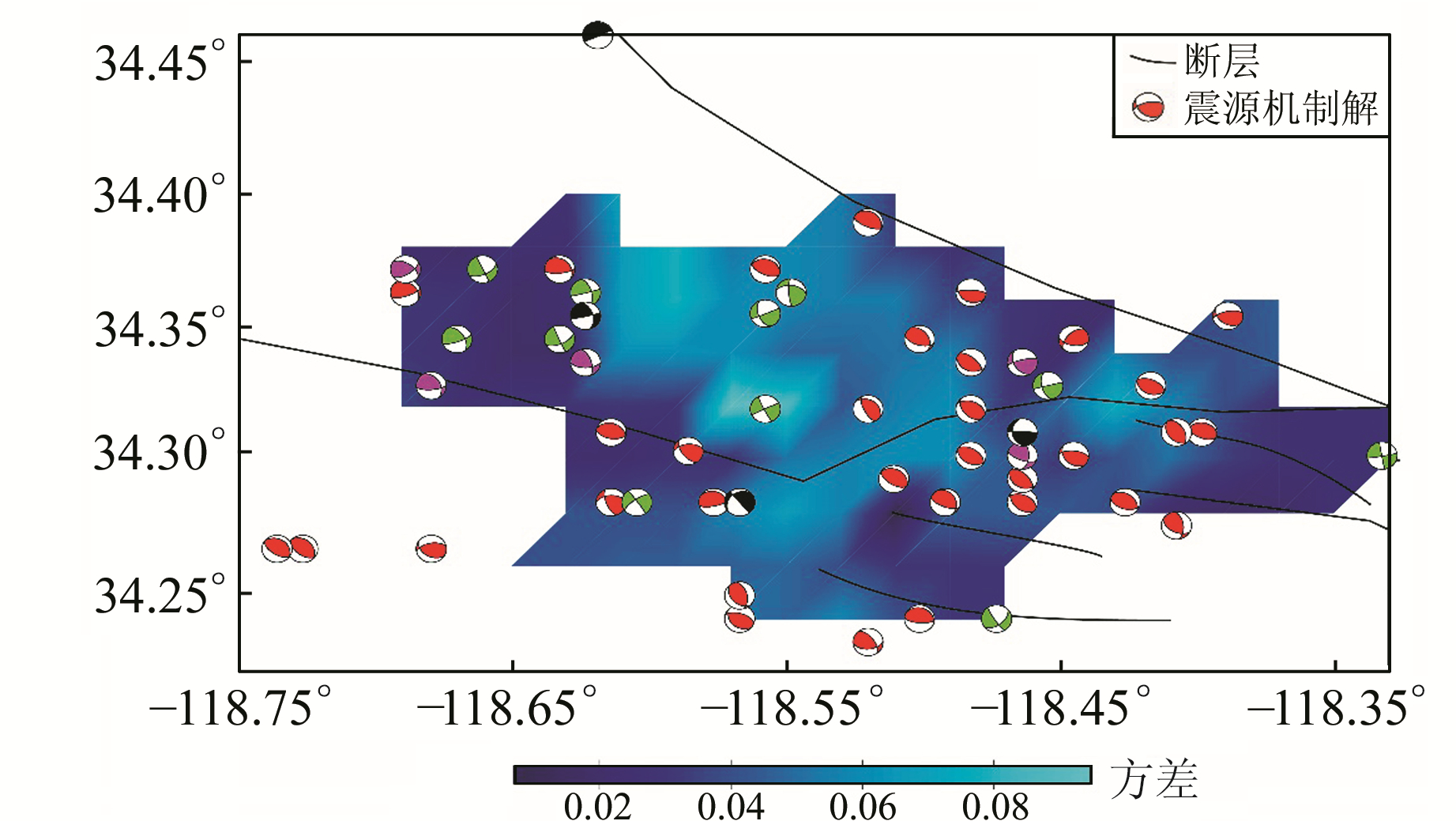
图 5中同时给出了震源机制解和应力张量方差的分布。可以看出,应力张量方差值大的地方震源机制解(如类型)比较复杂。也就是说,应力张量方差值大可能是由个别参与反演计算的震源机制解差异性较大引起的。为了验证这一猜想,将应力张量方差值较大地方的那些明显异于周围震源机制解的数据(图 5中黑圈标出的6个地震,即异常数据)尝试着剔除,其余的数据称为剔除异常数据组,再以相同网格划分和参数设置,运用区域分网格反演模块进行反演计算,结果见图 6和图 7(图中震源机制解符号含义同图 2)。可以看出,在剔除了异常数据后,北岭震源区最大主应力方位分布的变化不大,方向的一致性较剔除前有所改善,最大主应力方向为近南北向的情况几乎没有(图 6)。对比图 5和图 7可以看出,剔除异常数据后应力张量方差值明显变小,整个研究区的应力张量方差值均小于0.1。
|
图 6 剔除异常数据后北岭震源区最大主应力方位分布图 Fig. 6 The distribution of maximum principal stress orientation in source region after deleting abnormal data |
|
图 7 剔除异常数据后北岭震源区应力张量方差分布图 Fig. 7 The distribution of stress tensor variance in source region after deleting abnormal data |
在初步反演计算中,最优应力张量反演模块给出的中间主应力和最小主应力的置信区间很大。对于剔除异常数据组,同样运用最优应力张量反演模块进行反演计算,以观察各主应力方位的置信区间的变化。为便于对比,具体计算结果列于表 1。图 8(a)给出了3个主应力方向及其95%的置信区间(图 8中彩色区域为各主应力轴方位95%的置信区间)。可以看出,剔除异常数据后,最大主压应力方位仍为北北东向,平均剪滑角β为21.4°,较初步反演结果有所减小,但是中间主应力和最小主应力的置信限范围依然很大。因此,仅从空间平面展布上来剔除少量异常数据,其反演结果并不理想,需要更多的参考信息进行进一步分析。

|
图 8 剔除异常数据及分组反演结果给出的主应力轴及其置信区间 Fig. 8 The principal stress axes and their confidence regions after deleting abnormal data and inversion result by group |
2) 按震源深度分组
除板块俯冲带上的地震外,地震都发生在相对很薄的地壳内,地震在深度上的分布范围远小于在平面上的分布范围,加之震源深度定位上的误差以及震源体的大小,使得很难利用震源机制解研究构造应力状态随地壳深度的变化,因此,前人的研究也大都是从余震的平面分布上来分析应力场的分布特征。
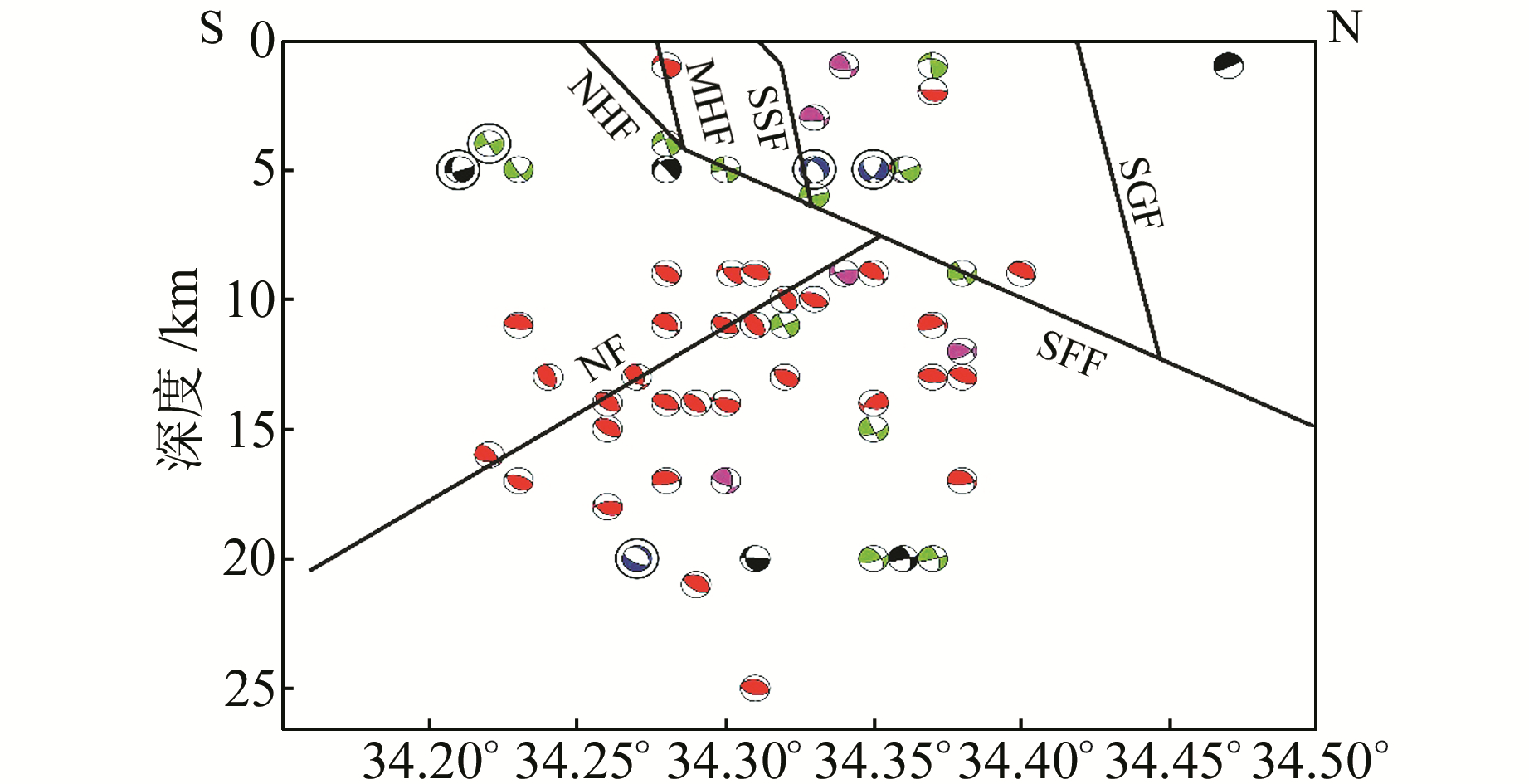
Thio等[8]在计算北岭地震余震震源机制解的同时,对余震震源深度进行了修正。本文尝试将62个余震震源机制解和根据前人给出的断层构造共同绘制在深度剖面中(见图 9,为便于与其他图件对比,震源机制解的投影没有变换,仍是从地表看到的投影;图中震源机制解符号含义同图 2,圆圈标注的为异常数据,断层根据Fuis等[12]的结果重新绘制)。从图 9中可以看出,62个余震震源机制解与断层构造有着较好的对应关系,逆走滑型和逆断型震源机制解大多位于圣弗尔南多地震断层以下的深部,而圣弗尔南多地震断层以上地壳浅部的余震震源机制解类型则比较复杂,并且前文6个异常数据中有5个位于研究区浅部。另外,Tsutsumi等[6]的研究结果表明,北岭地震断层没有破裂至地表,大约在5~8 km处被圣弗尔南多地震断层所截断。这就提示我们将62个余震震源机制解按其深度进行分组反演计算,以分析震源区地壳深浅部构造应力状态的差异以及与断层构造的关系。
|
图 9 余震及断层构造的深度剖面图 Fig. 9 The cross section of aftershocks and fault structures |
以震源深度8 km为界,将62个余震震源机制解分为深部和浅部2组(其中深部数据组剔除了图 9中的1个深部异常数据)。运用区域分网格反演模块(网格划分和参数设置与前文相同)对深部数据组进行反演的计算结果显示,最大主应力方位分布的变化不大,仍是北北东向,一致性较好,并且应力张量方差值均小于0.1。对于深部数据组,最优应力张量反演模块给出的结果也列在表 1中,3个主应力方向及其95%的置信区间见图 8(b)。可以看出,相对于剔除异常数据组,3个主应力的方向没有太大的变化,但中间主应力和最小主应力的置信区间明显变小(图 8),平均剪滑角β减为17.0°,反演结果明显变好。
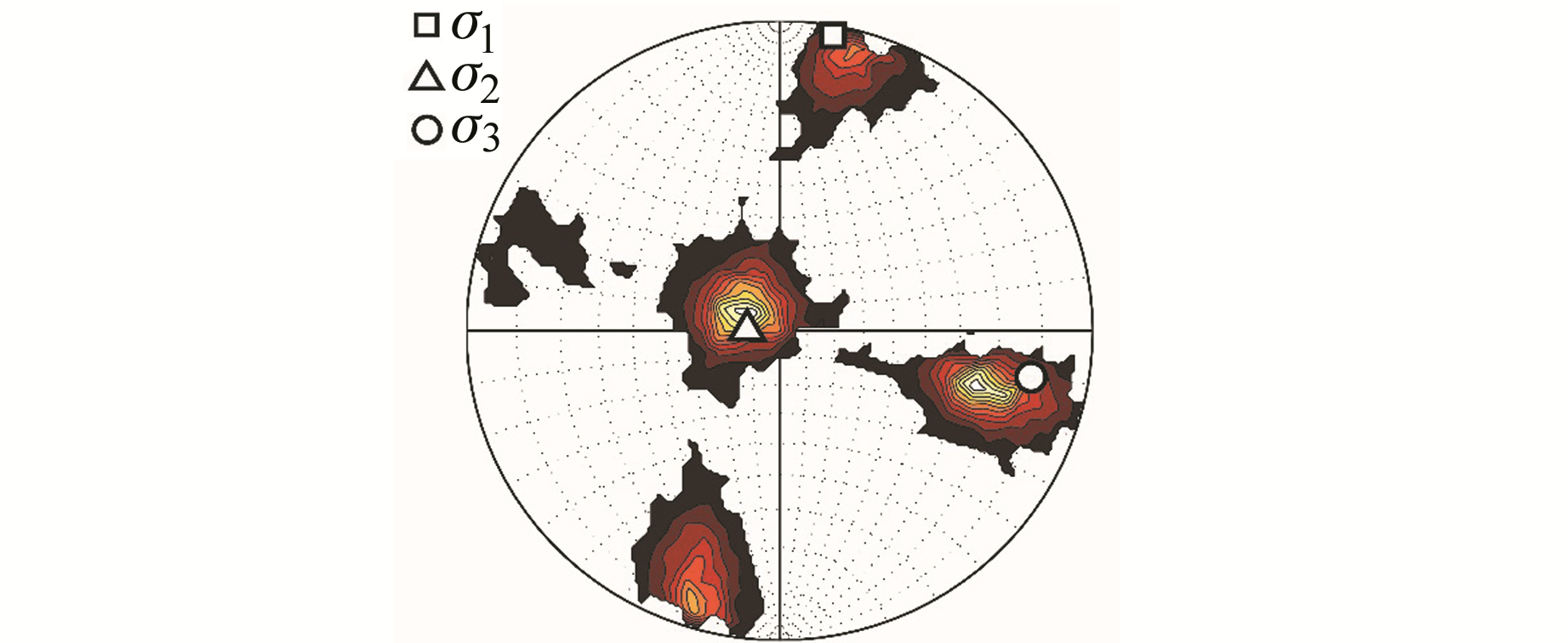
同样,运用最优应力张量反演模块,对浅部数据组进行反演计算,结果见图 10(图中彩色区域为各主应力轴方位95%的置信区间)和表 1。可以看出,浅部数据组的反演结果与深部数据组的明显不同,应力类型为走滑型,最大主应力仍为近水平,方向为北北东向,但中间主应力和最小主应力发生了变化,最小主应力的方位为101°,倾角为12°,并且3个主应力的置信区间比较大,平均剪滑角β为28.6°,表明反演结果的可靠性不是很好。另外,区域分网格反演模块给出的最大主应力方位分布也非均匀一致,大部分网格节点上的最大主应力为北北东向,但也有少部分网格节点上的最大主应力为北北西向。
|
图 10 北岭地区浅部主应力轴及其置信区间的下半球等面积投影 Fig. 10 Lower-hemisphere equal-area projections of principle stress axes and their confidence regions in shallow area of Northridge region |
本文以3种方式对1994年北岭MW6.7地震的余震震源机制解进行了反演计算,一是对Thio等[8]给出的62个余震震源机制解的初步计算;二是对剔除异常数据组的计算;三是将余震震源机制解分为深部数据组和浅部数据组的计算。对比3种方式下的4组反演结果(表 1)不难看出,4组反演结果有1个共同点,即最大主应力方向均为近水平,方位为北北东向,表明北北东向的水平挤压是北岭震源区构造应力状态的一个明确特征。
除了浅部数据组外,单从反演得到的最优应力张量上看,其余3组的结果很接近,但仔细对比不难发现,3组的反演结果给出的主应力方向的置信区间、平均剪滑角和应力张量方差还是有明显差异的。其中,深部数据组反演结果给出的置信区间明显优于剔除异常数据组和初步计算结果,平均剪滑角减小为17.0°,区域分网格反演模块给出的应力张量方差也很小。因此认为,将余震震源机制解分为深浅2个数据组进行反演计算的方式可能比较合理,即北岭MW6.7地震后,震源区深浅部的构造应力状态可能不完全一致,虽然深部和浅部的最大主应力方向均为北北东向,但震源区深部的应力类型为逆断型,震源区浅部的应力类型为走滑型。
前人利用地质构造分析、震源机制解分析、原地应力测量等多种手段对圣弗尔南多谷及其周边地区构造应力场进行了研究[9, 12-14]。结果显示,受太平洋板块的挤压作用,圣弗尔南多谷地区的最大主应力方向为北北东向,最小主应力接近垂直,与观察到的逆断层结构一致[14]。本文深部数据组的反演计算结果与该地区构造应力场的研究结果相吻合,这可能表明,北岭MW6.7地震后,震源区深部构造应力状态并未发生明显的改变,仍受区域构造应力场的控制。
浅部数据组反演结果给出的最大主应力方向仍为北北东向,但应力类型为走滑型,与震源区深部和区域构造应力场不一致。结合震源区构造,可以这样来理解这种应力的深浅差异和变化:发生MW6.7地震的北岭断裂没有破裂到地表,被圣弗尔南多断裂所截断,在震源区浅部(圣弗尔南多断层之上)还分布着多条高角度接近直立的断层(图 9),如北岭山断裂、圣盖博断裂和圣苏珊娜断裂等[8];地壳应力与构造及其运动密切相关,北岭MW6.7地震是逆冲型地震,地震发生后,在区域构造应力的作用下,震源区应力继续释放,隐伏的北岭断裂(可能包括其周围的小断层)继续逆冲运动,从而产生了一些逆冲型的中小余震,因此深部数据组的反演结果与区域构造应力场相一致,构造应力状态没有发生明显的改变;虽然北岭主震破裂没有冲过圣弗尔南多断裂,但北岭断裂的逆冲运动有可能引起了震源区浅部应力状态的变化,触发了浅部断裂的活动,由于浅部断裂近直立,更易于产生走滑运动。另外,从图 9可以看出,与深部明显不同,浅部的走滑型震源机制解占了相当的比重,同时还有多种类型的震源机制解。浅部数据组的反演结果显示,3个主应力方向的置信区间和平均剪滑角比较大(图 10,表 1),区域分网格反演模块给出的最大主应力方位分布也非均匀一致,表明MW6.7主震引起的浅部构造应力状态的变化也很可能是不均匀的,给出的3个主应力方向的不确定性较大。
基于本文的研究可以认为,对于类似北岭余震震源机制解这样比较复杂的震源区,简单机械地使用应力张量反演方法进行计算,其结果的可靠性可能不是很好,只有结合震源区地震构造和震源机制解分布情况,采用科学的分析思路,进行细致的反演计算,才能获取比较合理的结果。
由于本研究所选取的震源机制解主要集中在北岭震源区,且时间跨度较短,所以反演结果可能只是反映了北岭震源区构造应力状态在短时间内的局部变化特征。
5 结语1) 北岭地震后,震源区最大主应力为近水平,方向为北北东向,表明北北东向的水平挤压是北岭震源区构造应力状态的一个明确特征,与前人结果较为一致[9, 14]。
2) 从主应力方向的置信区间、平均剪滑角和应力张量方差这3个参数来看,将余震震源机制解分为深浅2个数据组得到的反演计算结果,其可靠性明显优于利用62个余震震源机制解直接进行反演计算得到的初步结果,表明北岭地震后震源区深浅部的构造应力状态可能不完全一致,虽然深部和浅部的最大主应力方向均为北北东向,但震源区深部的应力类型为逆断型,震源区浅部的应力类型为走滑型,深部数据组的反演结果与区域构造应力场相一致。
3) 北岭地震后震源区深浅部构造应力状态的差异可能与震源区的地震构造和北岭主震的错动方式有关,北岭主震是逆冲型地震,地震发生后,在区域构造应力的作用下,震源区应力继续释放,隐伏的北岭断裂(可能包括其周围的小断层)继续逆冲运动,从而产生了一些逆冲型的中小余震,深部构造应力状态没有发生明显的改变;虽然北岭主震破裂没有冲过圣弗尔南多断裂,但北岭断裂的逆冲运动有可能引起了震源区浅部应力状态的变化,触发了浅部断裂的活动,由于浅部断裂近直立,更易于产生走滑运动, 并且浅部构造应力状态的变化也很可能是不均匀的。
致谢: 本文的计算和相关图件的绘制均采用ZMAP软件包实现,在此对软件包作者和软件下载平台(http://www.seismo.ethz.ch/)表示感谢。
| [1] |
许忠淮. 用滑动方向拟合法反演唐山余震区的平均应力场[J]. 地震学报, 1985, 7(4): 349-361 (Xu Zhonghuai. Mean Stress Filed in Tangshan Aftershock Area Obtained from Focal Mechanism Data by Fitting Slip Directions[J]. Acta Seismologica Sinica, 1985, 7(4): 349-361)
(  0) 0) |
| [2] |
Ickrath M, Bohnhoff M, Bulut F, et al. Stress Rotation and Recovery in Conjunction with the 1999 Izmit MW7.4 Earthquake[J]. Geophysical Journal International,, 2014, 196(2): 951-956 DOI:10.1093/gji/ggt409
(  0) 0) |
| [3] |
胡幸平, 崔效锋. 华北地区中部地震精定位与构造应力场研究[J]. 震灾防御技术, 2013, 8(4): 351-360 (Hu Xingping, Cui Xiaofeng. Study on Earthquake Relocation and Tectonic Stress Field in Central North China[J]. Technology for Earthquake Disaster Prevention, 2013, 8(4): 351-360 DOI:10.3969/j.issn.1673-5722.2013.04.002)
(  0) 0) |
| [4] |
Michael A J. Use of Focal Mechanisms to Determine Stress: A Control Study[J]. Journal of Geophysical Research: Solid Earth, 1987, 92(B1): 357-368 DOI:10.1029/JB092iB01p00357
(  0) 0) |
| [5] |
Michael A J. Spatial Variations in Stress within the 1987 Whittier Narrows, California, Aftershock Sequence: New Technique and Results[J]. Journal of Geophysical Research: Solid Earth, 1991, 96(B4): 6303-6319 DOI:10.1029/91JB00195
(  0) 0) |
| [6] |
Tsutsumi H, Yeats R S. Tectonic Setting of 1971 Sylmar and 1994 Northridge Earthquakes in the San Fernando Valley, California[J]. Bullentin of the Seismological Society of America, 1999, 89(5): 1232-1249
(  0) 0) |
| [7] |
Mori J, Wald D J, Wesson R L. Overlapping Fault Planes of the 1971 San Fernando and 1994 Northridge, California Earthquakes[J]. Geophysical Research Letters, 1995, 22(9): 1033-1036
(  0) 0) |
| [8] |
Thio H K, Kanamori H. Source Complexity of the 1994 Northridge Earthquake and Its Relation to Aftershock Mechanisms[J]. Bulletin of the Seismological Society of America, 1996, 86(1): 84-92
(  0) 0) |
| [9] |
Zoback M L. First-and Second-Order Patterns of Stress in the Lithosphere: The World Stress Map Project[J]. Journal of Geophysical Research: Solid Earth, 1992, 97(B8): 11703-11728 DOI:10.1029/92JB00132
(  0) 0) |
| [10] |
Wiemer S. A Software Package to Analyze Seismicity: ZMAP[J]. Seismological Research Letters, 2001, 72(3): 373-382 DOI:10.1785/gssrl.72.3.373
(  0) 0) |
| [11] |
Lu Z, Wyss M, Pulpan H. Detail of Stress Directions in the Alaska Subduction Zone from Fault Plane Solutions[J]. Journal of Geophysical Research: Solid Earth, 1997, 102(B3): 5385-5402 DOI:10.1029/96JB03666
(  0) 0) |
| [12] |
Fuis G S, Clayton R W, Davis P M, et al. Fault Systems of the 1971 San Fernando and 1994 Northridge Earthquakes, Southern California: Relocated Aftershocks and Seismic Images from LARSE Ⅱ[J]. Geology, 2003, 31(2): 171-174 DOI:10.1130/0091-7613(2003)031<0171:FSOTSF>2.0.CO;2
(  0) 0) |
| [13] |
Dibblee Jr T W. Geology of the Santa Moncia Mountains and Simi Hills, California[C].South Coast Geological Society, California, 1982
(  0) 0) |
| [14] |
Hardebeck J L, Hauksson E. Crustal Stress Field in Southern California and Its Implications for Fault Mechanics[J]. Journal of Geophysical Research: Solid Earth, 2001, 106(B10): 21859-21882 DOI:10.1029/2001JB000292
(  0) 0) |
2. Earthquake Administration of Yunnan Province, 148 Beichen Road, Kunming 650225, China;
3. Department of Earthquake Science, Institute of Disaster Prevention Science and Technology, 465 Xueyuan Street, Beijing 101601, China;
4. Institute of Geophysics, CEA, 5 South-Minzudaxue Road, Beijing 100081, China
 2017, Vol. 37
2017, Vol. 37



