地球内部板块运动复杂，在板块运动过程中，往往会发生局部的点位变化信息。通过对某一区域的地壳形变进行研究，建立研究区域的运动场模型，给出研究区域任何点的速度或形变信息，从而为后续的地壳运动、地震预报^[1]等研究提供参考资料。

在地壳形变分析中，由于地壳运动有着明显的趋势性，可以基于欧拉矢量模型得到研究区域的水平形变场。但利用欧拉矢量模型的前提是假设研究区域板块划分可靠且为刚体，而任何板块在运动过程中都会存在一定程度的局部形变，欧拉矢量模型难以估计每一点的点位变化信息。近年来，国内外学者提出三角形内插法、有限元插值法及多面函数法对地壳水平和垂直形变进行了相关的研究分析^[2]。有限元法对剖分和插值函数的确定具有不确定性^[2]，而多面函数拟合过程中的参数选择往往带有不确定性，需要不断实验才能获得最佳的拟合参数。地壳运动除了具有整体性趋势外，还具有复杂的局部点位变化信息。Trarup提出了最小二乘配置方法(least squares collocation, LSC)^[3]。为了兼顾形变场局部点位的变化信息，滕金阳一郎首次将最小二乘配置应用于地壳形变分析中。该方法能够同时顾及大尺度地壳运动趋势项和小尺度地壳随机变化部分，得到广泛应用^{[2, 4-8]}。但由于仪器、观测环境等原因，观测数据不可避免地存在误差，由观测数据组成的系数矩阵不可避免地带有随机误差。因此，仅考虑到观测向量含有误差的最小二乘配置方法解算的结果并非最优解。

考虑到趋势项系数矩阵存在误差的情况，本文研究了总体最小二乘配置方法(total least squares collocation, TLSC)，该方法考虑了趋势项系数矩阵和观测向量均含有误差的情况，且把局部点位的变化信息作为信号纳入函数模型。通过模拟的地壳水平形变和意大利实际地震算例，对总体最小二乘配置与最小二乘配置方法的拟合推估效果进行分析和比较。

1 总体最小二乘配置迭代算法

根据广义最小二乘原理，观测方程可表达为：

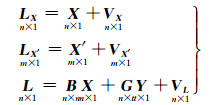
(1)

式中，L为观测向量；X为已测点信号，X′为未测点信号；L_X、L_X′分别为X和X′的虚拟观测值的先验期望，均等于0；V_X、V_X′分别为虚拟观测向量误差，V_L为观测向量误差；B为n阶单位矩阵，GY为趋势项。式(1)仅考虑了观测向量含有误差的情况，然而由于仪器精度、观测环境等原因，含有观测数据的趋势项系数矩阵G也存在误差。顾及系数矩阵含有误差的情况，建立广义总体最小二乘原理下的观测方程：

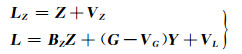
(2)

将系数矩阵误差V_G按列拉直，然后与观测向量误差V_L组成一误差向量e。将式(2)整理得：

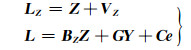
(3)

式中，L_Z=[L_X, L_X′]^T; Z=[X, X′]^T; V_Z=[V_X, V_X′]^T; B_Z=[B, 0]；C=[I_n, -(Y^T⊗I_n)]; e=[V_L, vec(V_G)], vec表示矩阵按列拉直，顺序从左到右。

随机模型为：

(4)

式中，σ₀²为验后单位权方差，P由观测向量权阵及系数矩阵权阵构成。广义总体最小二乘平差准则为：

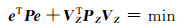
(5)

其中有L_Z=Z+V_Z，L_Z=0，因此平差准则可表达为：

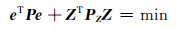
(6)

式中，

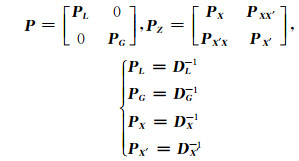
(7)

其中，P_L、D_L分别为观测向量权阵和方差阵，P_G、D_G分别为系数矩阵权阵和方差阵，P_X、P_X′分别为已测点信号与推估点的权阵，D_X、D_X′和D_X′X分别为已测点信号协方差阵、推估点信号协方差阵和推估点信号与已测点信号的协方差阵。按求函数条件极值的方法组成函数：

(8)

分别对Φ求偏导数，令其等于0，并对方程式进行整理，得：

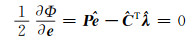
(9(a))

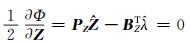
(9(b))

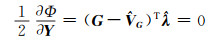
(9(c))

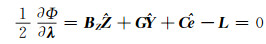
(9(d))

由式(9(a))、(9(b))得:

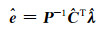
(10(a))

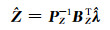
(10(b))

把式(10)代入式(9(d))得：

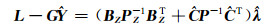
(11)

由式(11)得：

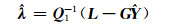
(12)

其中，。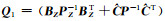

由式(10(a))和式(12)得：

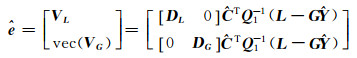
(13)

由式(9(c))和式(12)得：

(14)

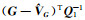
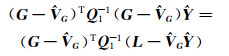
式(14)左乘得：

(15)

由式(15)即可导出趋势项参数Ŷ的表达式：

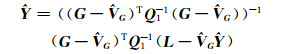
(16)

总体最小二乘配置迭代算法步骤如下。

1) 由最小二乘配置法求出趋势项参数Ŷ⁽⁰⁾作为初始值，ê⁽⁰⁾=0：

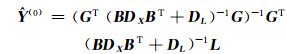
(17)

2) 计算相关参数：

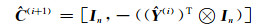
(18(a))

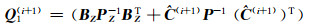
(18(b))

(18(c))

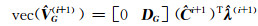
(18(d))

(18(e))

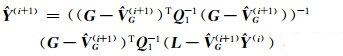
(18(f))

式中，reshape表示把系数矩阵改正数重构成系数矩阵G的形式。

3) 当‖Ŷ⁽ⁱ⁺¹⁾-Ŷ⁽ⁱ⁾‖≤δ(δ为预设的阈值)时，迭代结束；否则把Ŷ⁽ⁱ⁺¹⁾作为初始值，重复步骤2)~3)，直至满足条件。

4) 由式(10(b))及式(12)可得随机信号参数的表达式：

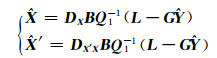
(19)

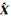
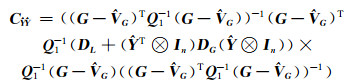
5) 计算Ŷ、和的方差：

(20)

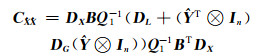
(21)

(22)

式中，⊗为Kronecker积。

2 算例分析 2.1 模拟算例

在边长为100 km的正方形区域，分别沿X和Y方向等距取样12个点，共获取144个坐标点(图 1所示)。利用MATLAB函数linspace在区间[0.016 m, 0.024 m]取样288个值，前144个点作为X方向的位移真值，后144个点作为Y方向的位移真值。随机选取100个点作为已测点，其余44个点为检核点。给已测点位移加入均值μ₁=0、标准差σ₁=0.003 m的高斯误差，获得水平观测位移。其中X和Y方向的位移与坐标值之间的关系为：

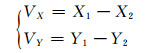
(23)

式中，V_X、V_Y分别为X和Y方向上的位移，X_i、Y_i(i=1, 2)分别表示某点第i期监测网观测坐标值。

假设每期观测坐标精度一致，由式(23)可知水平位移与坐标值之间的关系。根据协方差传播定律，它们的方差关系式为：

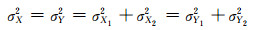
(24)

式中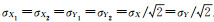，。因此，坐标真值加入均值μ₂=0、标准差的高斯误差，共获得144个点的观测坐标。

假设地壳形变是空间连续变形，在空间上距离越近的点，其点位变化相关性越强，反之其相关性越弱。利用高斯函数作为协方差函数^[6]，东向和北向的信号协方差函数分别为：

(25)

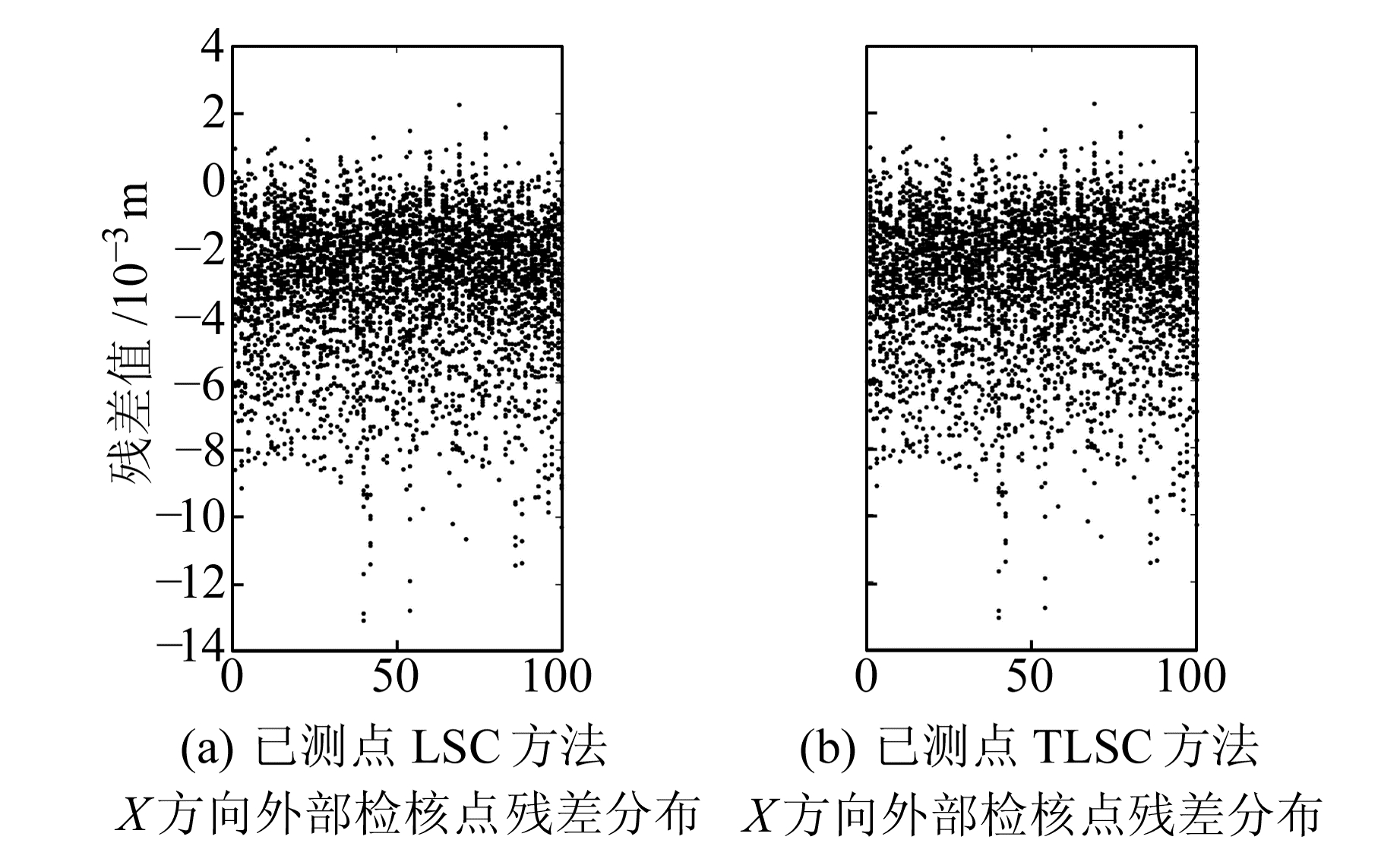
为了避免因为引入随机误差对解算结果带来的影响，实验模拟100次。利用TLSC和LCS方法进行拟合推估，欧拉矢量参数^[2]如表 1所示。两种方法的已测点及外部检核点残差统计见表 2和表 3，已测点及外部检核点残差分布如图 2和3所示。由于两种方法X、Y向计算结果基本一致，限于篇幅，本文只给出X方向残差图。

2.2 意大利L’Aquila地震的垂直形变场

2009-04-06意大利中部Abruzzo大区的L’Aquila发生了6.3级地震。这次地震造成意大利人民巨大的损失，其中致使300多人死亡，1 000多人受伤，2万多人流离失所^[9]。本文分别利用TLSC方法和LSC方法对意大利L’Aquila地震的InSAR同震形变数据进行计算分析和比较。其中，Envisat卫星Track 129干涉得到的1 282个点沿视线向形变值数据来源于文献[9]，形变量中误差为6.8 mm。随机选取100个点作为外部检核点，其余1 182个点作为已测点，所有数据如图 4所示。

实际所获得的InSAR数据是沿视线向的形变值，并不是我们所需要的垂直方向的形变值。根据视线向形变值与垂直形变值之间的关系，将1 282个点的视线向形变值转化为垂直形变值，具体转换公式如下：

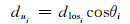
(26)

式中，d_ui为第i点视线向形变值分解到垂直方向的形变值，d_losi为第i点雷达视线向形变值，θ_i为第i点雷达波入射角。根据式(26)和误差传播定律，得到各点垂直形变的中误差。假设地壳垂直形变近似各向同性，则拟合的信号协方差函数为：

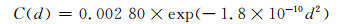
(27)

利用TLSC和LSC方法进行拟合推估，两种方法的趋势项参数、外部检核点残差统计分别如表 4、表 5所示，外部检核点残差分布如图 5所示。

2.3 分析讨论

从上述的模拟算例和意大利L’Aquila实际地震算例中可以看到，TLSC和LSC方法计算的参数、残差统计表和残差分布图的结果均基本一致，即总体最小二乘配置与最小二乘配置方法的拟合推估效果基本一致。造成这样的情况有以下原因：

1) 在地壳形变分析中，从表 1和表 4可以看出，利用最小二乘配置方法解算的趋势项参数解为一个接近0的小值，以一个小值作为总体最小二乘配置迭代算法的初始值，尽管迭代条件δ=10^-12为一个极小值，计算过程没有发生迭代。再者，把迭代条件设定为一个更小的值δ=10^-20，从而使得计算发生迭代，但总体最小二乘配置解算的参数解同样为一个接近于0的小值，与最小二乘配置方法解算的参数解依然十分接近，导致总体最小二乘配置与最小二乘配置方法在拟合效果上基本一致。

2) 利用InSAR技术手段获取大面积的测量数据资料，获得的观测对象坐标值量级通常较大(本文大部分观测坐标量级达10⁵以上)，由TLSC方法计算的系数矩阵误差改正值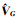量级在区间[10^-20，10^-3]之内，系数矩阵误差对数值量级大系数矩阵的影响可忽略不计，这也是总体最小二乘配置方法针对系数矩阵误差改正效果并不明显的原因。

3) 文献[10]研究了系数矩阵误差对PEIV模型平差结果的影响，并得到了相关的理论成果。该理论认为，分配给系数矩阵随机元素的多余观测数r_G和分配给观测向量的多余观测数r_L的大小与系数矩阵误差引起的模型方差D_G=(Y_LSC^T⊗I_n)D_G(Y_LSC⊗I_n)和观测向量误差引起的模型方差D_L的相对大小有关。当D_G的量级远远大于D_L时，r_G趋向于r，而r_L趋向于0，此时系数矩阵误差对模型平差起主要作用；反之，当D_G的量级远小于D_L时，r_G趋向于0，r_L趋向于r，此时观测向量误差对模型平差起主要作用。本文模拟的地壳水平形变中，D_G的量级达到了10^-19，远小于D_L的10^-5；同样，在意大利地壳垂直形变中，D_G的量级达到10^-17以上，而D_L的量级为10^-5，从而导致不管是模拟的地壳水平形变还是意大利实际地震算例，分配给系数矩阵的多余观测数r_G均接近0。考虑到系数矩阵误差的总体最小二乘配置计算的效果优势并不明显，与最小二乘配置计算结果基本一致。

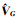
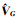
同样，在文献[11-12]坐标转换以及文献[13-14]应变参数反演的应用中，也存在利用顾及系数矩阵误差的总体最小二乘方法得到的计算参数精度与传统的最小二乘方法基本一致的情况。这类问题都有一个相同之处，其构成系数矩阵的数值大部分为一个数量级较大的值，而对应的算法计算的误差改正数却为一个极小值。本文中≈0，观测误差改正值对观测值本身的影响十分有限；其次，本文中两个算例的系数矩阵误差方差D_G≈0，把=0及D_G=0代入式(18(f))，则此时TLSC的趋势项参数表达式退化为LSC参数表达式，导致本文TLSC方法与LSC方法的效果基本一致。文献[10]给出了一个严密的理论依据，当系数矩阵误差方差D_G=(Y_LSC^T⊗I_n)D_G(Y_LSC⊗I_n)相对观测向量误差方差D_L为一个小值时，分配给系数矩阵的多余观测数r_G均接近0，顾及系数矩阵误差的总体最小二乘配置与传统的最小二乘配置方法计算结果基本一致。但是，总体最小二乘配置方法是对配置理论的一个重要补充和完善，具有重要的理论意义。

3 结语

本文推导了总体最小二乘配置方法，并应用于地壳形变分析中。相对于最小二乘配置方法仅考虑到观测向量存在随机误差的情况，总体最小二乘配置方法同时顾及到观测向量和趋势项系数矩阵存在随机误差的情况。从理论上来说，总体最小二乘配置方法比最小二乘配置方法更为严密。

本文通过总体最小二乘配置与最小二乘配置计算的参数结果、系数矩阵的量级大小与对应的误差改正值量级大小之间的关系作出理论分析，当系数矩阵误差改正值及系数矩阵误差方差约等于0(即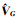≈0和D_G≈0)时，总体最小二乘配置退化为最小二乘配置。

本文推导的总体最小二乘配置方法作为配置理论的重要补充和完善，其在大地测量数据处理领域的适用情况还需作进一步的研究和验证。